Journal of Water Resource and Protection
Vol.07 No.04(2015), Article ID:54667,15 pages
10.4236/jwarp.2015.74028
Vadose Zone Heterogeneity effect on unsaturated Water Flow modeling at Meso-scale
Artur Paiva Coutinho1,2, Laurent Lassabatere1, Thierry Winiarski1, Jaime Joaquim da Silva Pereira Cabral2, Antonio Celso Dantas Antonino2, Rafael Angulo-Jaramillo1
1LEHNA, UMR 5023 CNRS, ENTPE, UCB-Lyon-1, Vaulx-en-Velin, France
2Universidade Federal de Pernambuco, Centro de Tecnologia e Geociências, Programa de Pós Graduação em Engenharia Civil/Tecnologia Ambiental e Recursos Hídricos, Recife, Brasil
Email: laurent.lassabatere@entpe.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 February 2015; accepted 13 March 2015; published 16 March 2015
ABSTRACT
The understanding of unsaturated flow in heterogeneous formations is a prerequisite to the understanding of pollutant transfer in the vadose zone and the proper management of infiltration basins settled over such heterogeneous formations. This study addresses the effect of lithological heterogeneity of a glaciofluvial deposit on flow in the vadose zone underneath an infiltration basin settled in the Lyon suburbs. The basin had already been the subject of several previous studies, some of which demonstrated the impact of soil heterogeneity. But all of them were only based on the sedimentological study of a trench and no study addressed the potential spatial variability of results due to the spatial variability of soil heterogeneity. In this study, we model flow in the vadose zone for several case studies, including drainage, water infiltration during a rainfall event, and a complete meteorological chronic. These calculations were conducted for several sections, previously characterized in the basin using GPR and sedimentological study and compared with a blank (homogeneous section). The results clearly show that heterogeneity impacts unsaturated flow and that these impacts depend upon the section considered. Some geometrical architectural and textural parameters were proposed to explain the spatial variability and effect of the soil heterogeneity on unsaturated flow, thus establishing the first step towards modeling unsaturated flow in the basin at the meso-scale.
Keywords:
Architectural and structural indicators, Ground penetration radar,numerical Modeling, preferential Flow, Structural heterogeneity, unsaturated Flow

1. Introduction
Nowadays cities expand as a result of urbanization. The extension of urbanization and sealed surface results in the modification of the water cycle, and the volumes produced by the sealed surface are too important to be collected and treated in usual stormwater plants. To alleviate such problems, best management practices have been developed, most of which are based on the infiltration of runoff water in infiltration basins or pits. Infiltration basins must be settled over permeable soils to allow water infiltration. Recently, the effects of infiltration basin on water cycle and on the quality of groundwater and the soil below have been questioned [1] . A particular care must be taken about the pollutants carried by runoff water (heavy metals, organics, etc.) that can be responsible for the degradation of the quality of the soils.
In the east plain of Lyon (France), infiltration basins are commonly used to infiltrate runoff water. In this region, most infiltration basins were settled over a glaciofluvial deposit, as a result of ancient glaciation periods and the action of the Rhone River. This glaciofluvial deposit has proved to be highly heterogeneous and made of contrasting material in terms of sedimentological properties. Goutaland et al. [2] [3] and Winiarski et al. [4] have proposed a methodology to assess flow and pollutant transfer in such heterogeneous media. The first step consists of describing the sedimentological properties of the heterogeneous media using geophysical tools. Ground penetrating radar (GPR) can be used as a non-destructive tool for investigating glaciofluvial deposits in detail up to a depth of 20 m [5] [6] . GPR allows the documentation of the internal structure (bedding geometry) of active braided bars and channels under both saturated and unsaturated conditions [6] [7] . Using GPR, Goutaland et al. [3] proposed a methodology to identify the different units and materials, referred to as lithofacies, which constituted the deposit and dug a trench to validate their findings. Then, the same authors and colleagues used water infiltration experiments and best method [8] to derive the hydraulic properties of the lithofacies and to model drainage in the trench. On this basis, Winiarski et al. [4] coupled the modeling of flow with the hydrodispersive and geochemical properties of the lithofacies to predict pollutant transfer over the same section. These authors concluded that preferential flow was likely to establish, in particular under unsaturated conditions with capillary barrier induced funneled flows. They also concluded that preferential flow might impact significantly the transfer of pollutants and reduce the removal of pollutants by materials that were far from flow pathways. Indeed, it is well known that pollutant transfer in the soil is highly sensitive to flow pathways and flow heterogeneity since preferential flow may reduce the access of pollutants to reactive particles, e.g. [9] -[11] .
In these studies, the investigations were focused on the case of one sole section, for which the sedimentological information was validated with a trench. For this section, flow was modeled for several scenarios in terms of geometry (from a homogeneous section filled only with the main material to the most heterogeneous case with a full description including all lithofacies). If the results show that the heterogeneity plays a role, this must be confirmed with the study of several sections and scenarios. Indeed, only one section was investigated over an infiltration basin of 1.38 ha. To get an idea of the impact of preferential flow on the whole infiltration basin, we must get more information on the spatial variability of heterogeneity of sedimentological properties of the deposit and the effect of such variability on preferential flow.
In this study, we focus on the impact of sedimentological heterogeneity on unsaturated flow. For that purpose, we have scanned the ground with GPR over several sections and we have modeled the flow in these different sections and compared the results with the flow in a homogeneous section containing the main material. Several hydric and hydraulic conditions were tested: drainage, water infiltration (with fixed water flux) and a complete meteorological chronic of the first 1000 hours of 2008. We aim to understand and characterize the effect of soil heterogeneity on flow in the vadose zone, and in particular its effect on flow pathways and fluxes at surface for several kinds of heterogeneous soil profiles. In addition to the analysis of water pressure and fluxes in the profile and at surface, quantitative indicators are proposed to link flow pattern to the lithological heterogeneity of studied sections. These indicators are designed to summarize the architecture of the heterogeneous sections and are expected to serve as explanatory factors for flow pattern, with the final aim to be used as tools for the prediction of flow response to lithological heterogeneity. This is the first step in understanding and modeling of flow heterogeneity at the basin scale.
2. Materials and methods
2.1. Site location
The field site is a storm water infiltration basin, referred to as Django Reinhardt basin (DjR basin), and located in Chassieu, in the eastern suburbs of Lyon, France (Figure 1a)). The storm water catchment is an industrial area of 185 ha located south of Chassieu (Figure 1b)). The basin covers an area of 1.38 ha and is downstream from a storage and settling basin. This basin is located on quaternary deposits of a glaciofluvial corridor (southeast?northwest orientation), deposited during the last glacial maximum (Figure 1a)). The thickness of the deposit is approximately 30 to 35 m (Barraud et al., 2002). The deposit rests on an impervious substratum of tertiary mollassic sands. The groundwater level is at a depth of 13 m. The aquifer has a mean hydraulic conductivity of 7 to 9 × 10−3 m s−1 [12] . This site is instrumented by the Observatoire de Terrain en Hydrologie Urbaine (http://www.graie.org/othu/).
2.2. GPR Study
Ground penetrating radar (GPR) is a non-invasive geophysical technique that detects electrical discontinuities in the shallow subsurface. This technique is based on the generation, transmission, propagation, reflection and reception of discrete pulses of high frequency (MHz) electromagnetic energy. It allows the assessment of spatial structures of sediments to a depth of 10 to 20 m over extended areas [13] -[15] . Sedimentary geologists widely used this technique to reconstruct depositional environments and document historic sedimentary processes [16] . Indeed, glaciofluvial deposits are characterized by a textural heterogeneity derived from erosion, transport and sedimentation phases that have led to the formation of lithological units. In the present paper, the term lithofacies has been used as reference to lithological units of glaciofluvial deposits, all of these corresponding to a specific genetic unit (i.e., formed by a homogeneous process of transport and sedimentation, [17] ).
The GPR measurements were carried out using the GSSI SIR 3000 system (Geophysical Survey System Inc., Salem, USA), operated with a shielded antenna at a central frequency of 400 MHz and 200 MHz, running in
Figure 1. a) Geological settings of the eastern part of the Lyon area; b) location of site in the Chassieu city area. The DjR infiltration basin was settled over a 13-m-deep unsaturated glaciofluvial deposits and receive the waters from a storage and settling basin; c) Layout of the 5 m × 5 m rectilinear GPR acquisition grid that covers the infiltration basin.
monostatic mode. The data processing was performed using the GSSI Radan 7 software. This processing consisted of distance normalization, a static time shift (to align direct ground wave arrival to 0 ns), a background removal (to eliminate the high amplitude direct ground wave), and a Kirchhoff migration. The electromagnetic wave velocity was determined by CMP (common midpoint) with two 400 MHz antennas. According to Goutaland et al. [18] , a velocity of 0.09 m ns−1 was selected to convert two-way travel time into actual depth.
At our site, previous GPR investigations at 200, 400, and 900 MHz had been performed and compared to trench walls [18] [19] . These data were used to explore the ability to detect sedimentary structure at the scale of the required model resolution (i.e., at the lithofacies scale) and the penetration depth for each antenna. The best tradeoff between high resolution and adequate penetration depth was obtained with the 200 MHz antenna. Thus, only results obtained using the 200 MHz antenna are illustrated.
The 400 MHz and 200 MHz profiles were collected in a 5 m × 5 m grid pattern (Figure 1c)). The dimensions of the acquisition grid were 140 m × 110 m. The spacing between each grid line was set at 5 m. GPR measurements (400 MHz and 200 MHz) were performed on all acquisition grid lines. GPR data set were interpreted using radar facies analysis [18] in conjunction with the classification of seismic reflections developed by Mitchum et al. [20] . During interpretation of the profiles, constant gain was applied to the data to note the amplitude of reflections. The GPR profiles were exported into image file format (.bmp), and major reflections were traced out and colored using Illustrator CS6 drafting software (Adobe, Inc.). As GPR profiles acquired an immense amount of interpreted sedimentological information, only one major radar reflection package was described with the profiles of 200 MHz antennae. The profiles of 400 MHz antennae (not presented in this paper) were used to confirm the previous interpretations based on the 200 MHz antennae.
2.3. Numerical modeling offlow
Unsaturated flow was modeled for several sections, considering the first 4 meters of soil below several lines of the acquisition grid. Indeed, each acquisition line was interpreted and GPR data was precise enough to describe the deposit architecture in detail (i.e., lithofacies and relative positions) for ~4 meters. For each section (i.e., ~4 m of soil below the acquisition line), unsaturated flow in the deposit was modeled considering Richard’s equation and using HYDRUS 3D software [21] :
 (1)
(1)
where θ is the volumetric water content, h is the pressure head, x, y, and z are the spatial coordinates, t is time, and K is the unsaturated hydraulic conductivity tensor. We assumed isotropy for all lithofacies. Soil water retention and hydraulic curves are characterized by the van Genuchten-Mualem relation [22] :
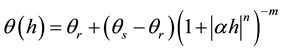 (2a)
(2a)
 (2b)
(2b)
where
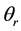 and
and
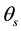 denote the residual and saturated water content, respectively; Ks and Kr are the saturated and relative hydraulic conductivity, respectively hg the scale parameter of water pressure heads, n is a pore-size distribution index, l is a pore-connectivity parameter, and a shape parameter m equal to 1-1/n. On the basis of the sedimentology description obtained with the method described above, each material was assigned the hydraulic properties proposed by Goutaland [2] . Hydraulic parameters are described in Table 1. In this study, the role of the coarser material (gravel) was neglected and this topic will be the subject of further studies.
denote the residual and saturated water content, respectively; Ks and Kr are the saturated and relative hydraulic conductivity, respectively hg the scale parameter of water pressure heads, n is a pore-size distribution index, l is a pore-connectivity parameter, and a shape parameter m equal to 1-1/n. On the basis of the sedimentology description obtained with the method described above, each material was assigned the hydraulic properties proposed by Goutaland [2] . Hydraulic parameters are described in Table 1. In this study, the role of the coarser material (gravel) was neglected and this topic will be the subject of further studies.
For numerical resolution, sections were meshed through triangular elements to build the reference 2D numerical domain, 30 m in length and 4 m in depth. Mesh elements dimensions never exceed 8cm and the number of nodes is in the order of 30,000 nodes. Each node was assigned a set of hydraulic accordingly to the sedimentological description of the trench. Boundary conditions were set at no flux on the side walls and free drainage at the bottom. Two events were modeled: drainage from a close to saturation initial state and water infiltration induced by fixed constant flux at surface, mimicking a rainfall event, using atmospheric boundary option. The initial condition was fixed at hi = −0.01 m for the drainage to simulate close to initial saturated condition and to −5 m for the rainfall event. In this study, the accumulation of water at soil surface was neglected. The maximum al-
Table 1. Hydrodynamic properties of the litohfacies.
lowed pressure head at the soil surface, that allows the calculation of the real water flux at the atmospheric boundary, was fixed at its default value, i.e., 0. Finally, modeling was conducted for real meteorological data recorded in 2008 at the station of Lyon Bon (France). Incoming flow rates (qenter) were calculated using rainfall and potential evaporation-transpiration intensities ( and
and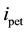 ), the catchment runoff coefficient (cR) and both catchment and basin surface areas (SC and SB), through: [23]
), the catchment runoff coefficient (cR) and both catchment and basin surface areas (SC and SB), through: [23]
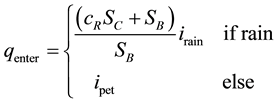 (3)
(3)
The runoff coefficient is fixed at a value of 0.4 and evaporation-transpiration was uniformly distributed all along the year.
3. Results and Discussion
3.1. Architectural characterization of the Studied Sections
A sedimentological description of glaciofluvial deposit was performed at both a textural and structural scale. The structural scale is the description scale of the sedimentary bodies, composed of distinctive assemblages of lithofacies and corresponding to the depositional product of a particular process or succession of processes occurring during a depositional system [17] . These sedimentary bodies are called architectural units or depositional units [24] . The textural scale aims at characterizing lithofacies that are defined as uniform strata characterized by their distinctive lithological features (composition, grain size, bedding characteristics, and sedimentary structures) and corresponding to an individual depositional event [17] .
Both lithofacies and depositional units of the studied glaciofluvial deposit have already been characterized by Goutaland et al. [18] for the studied deposit. These authors described the lithofacies using the sedimentological code of Miall [17] extended by Heinz et al. [24] . According to results obtained for a trench studied by Goutaland et al. [19] in the same infiltration basin, we interpreted six of the radar sections of the acquisition grid depicted in Figure 1 (Sections S1 to S6). Figure 2 shows one example of the radar profile interpretation (S1). The proposed interpretation was conducted considering the six depositional units proposed by Goutaland et al. [18] , namely units 1, 2, 3, 4, 5 and 6, from the base to the top of each section (Figure 2a)).
Two distinct levels were revealed over the first four meters of the glaciofluvial deposit (Figure 2b)):
・ An upper level (first ~0.5 m) corresponding to particle deposition at high stream energy, which lies at the origin of the presence of a very heterometric sand and gravel mix (Gcm lithofacies). This level comprises structural unit 6;
・ A lower level (located at a depth > ~0.5 m, on average) that corresponds to a braided proglacial system deposit, leading to such structures as paleochannel and scour fill (S-x, Gcm and Gcm, b lithofacies), and gravel progradations (Gcm, b lithofacies). This level comprises the structural units 1 - 5.
In these last units, three distinct lithofacies are present [18] : medium sands (S-x lithofacies), sand and gravel mixes, with a dominant heterometric gravel fraction (Gcm lithofacies) or with a bimodal grain size distribution (Gcm, b lithofacies). The sand and gravel mixes (Gcm, b lithofacies) constitute the predominant lithofacies of the glaciofluvial deposit. Goutaland et al. [19] provided a sedimentological interpretation of all lithofacies. The sands are low-flow regime deposits, whereas the Gcm, (b) lithofacies correspond to a high flow stage deposit. The Gcm, b lithofacies formed by gravel dunes migration resulted from gravel bars migration. These considerations allow us to define the edges of all lithofaciesin all studied sections. The identification procedure is depicted for a specific section in Figure 2b), and the results of such a procedure are depicted for all sections in Figure 3.
The different sections were described in terms of lithological heterogeneity using the following geometrical
Figure 2. a) Representative GPR profile with antenna 200 MHz and major GPR reflection patterns; b) Interpretative sketches of major lithofacies (Sx: sand; Gcm: sandy gravel; Gcm, b: sandy gravel bimodal).
structural or architectural indicators. These were defined in agreement with the architecture of the studied material and sections which were split into three generic elements: the predominant material, referred to as “main lithofacies” which occupies most of the section, the upper layer and sand lenses (Figure 3). For these elements, the following indicators are proposed (Figure 3):
 (4a)
(4a)
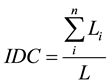 (4b)
(4b)
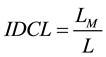 (4c)
(4c)
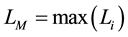 (4d)
(4d)
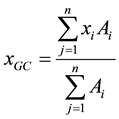 (4e)
(4e)
where SM, SLa, Ai and STC refer to the surface occupied by the main lithofacies, the upper layer, the ith sand lens and the total area of the whole section, respectively; Li corresponds to the length of the ith sand lens and xi to its abscissa (Figure 3). Indicators FM, FLa and FLe represent the degree of occupancy in the section by the main lithofacies, the upper layer (Figure 3, La) and sand lenses (Figure 3, Le), respectively; indicators IDC and IDCL quantify the degree of obstruction of the horizontal length by all inclusions or by the largest inclusion, and finally XGC defines the gravity center of the sand lenses.
On average, the upper layer occupies ~17% of the whole section and sand lenses ~ 21%. For most sections, the degrees of occupancy were close to average, except Section S4 with low values for both upper layer and sand lenses, Section S1 with a low degree of occupation for sand lenses, and Section S5 with a high degree of
Figure 3. Schematic lithologic representation of the 5 sections under study: the sections are filed with the main lithofacies (M), a sandy gravel bimodal referred to as Gcm, b, an upper layer (La) made of sandy gravel referred to as Gcm, and sandy lenses (Le) made of sand referred to as Sx. The sandy lenses are characterized by their length (Li), their position (xi) and their area (Ai) for the lens i (i = 1 to n, with n the total number of lenses).
occupation for both the sand and the upper layer. For the position of lenses, the sections were ranked in function to the placement of sand lenses (Figure 3). For the first section, sand lenses are either close to the right or left boundaries, with a gravity center close to the center (i.e., XGC = 13.2 » 15 m). Sections S2, S3 and S4 contain all sand lenses close to their left edge but with an increasing abscissa for the gravity center, corresponding to an increase in the degree of obstruction of the section length by sand lenses. The last section, S5, corresponds to a complete obstruction of section length, with the highest value of indicator IDC (Table 2). Clearly, sections exhibit different geometries and may influence flow in different ways.
3.2. Modeling water Redistribution during Drainage
We first modeled water redistribution in the whole profile during a drainage event. All soil profiles were considered close to saturation at the beginning of the event with a water pressure head of −0.01 m. Clearly, water redistribution depends on the profile. In Figure 4, the evolution of water content with time is illustrated for three contrasting profiles: a) uniform profile (Section H, Figure 4), b) heterogeneous profile with layered system
Table 2. values of geometrical parameters for the studied sections, H for homogeneous and the 5 heterogeneous sections from S1 to S5 are described in Figure 3.
Figure 4. Time evolution of water content in three sections during the drainage phase; the sections and their respective geometry are reminded at the upper part of the figure.
and inclusions mainly on the left (Section S1, Figure 4) and finally a layered profile with inclusions randomly distributed along the whole section (Section S5, Figure 4). It is clear that in the uniform profile, isolines for water content are horizontal lines, revealing a piston type drainage with homogeneity of processes over the whole section (Figure 4, A). On the contrary, in heterogeneous sections, the geometry of isolines for water content is impacted by the geometry of inclusions and reveals that inclusions store water (Figure 4, B and Figure 4, C). At time zero, there is higher water content in sand lenses and in the upper layer (Figure 4, D). Indeed, at the beginning, all lithofacies are close to saturation and saturated water content is higher for the sand and the Gcm constituting the upper layer (Table 1, lithofacies S-x and Gcm, respectively). Saturated water content lies at 0.274 and 0.359, respectively for the upper layer and the sand lenses, versus 0.186 for the main lithofacies. Thus, it seems logical to get higher water content in the upper layer and the sand lenses at the beginning. For longer times, drainage remains the same in the main material, with water content similar to that obtained for the uniform section. On the other hand, drainage seems to slow down in the sand lenses, with higher water content during the whole drainage phase. When time equals 336 h, clearly the sand lenses store water in heterogeneous profiles S3 and S5 (Figure 4, E and Figure 4, E').
Water fluxes are now described and explained. At upper boundary, water fluxes are null by definition (drainage and no flux entering at surface). At lower boundary, fluxes decrease with time and tend towards zero (Figure 5b)). The differences between sections are really tiny. At the beginning of the process (i.e., between 0 and 5 h), flow rate is a little bit faster in the homogeneous section (Figure 5b)). After ten hours, the flow rate for the homogeneous sections decreases faster and becomes slightly below flow rates for the other sections. The following conclusions can be stated on the basis of the analysis of cumulative fluxes (Figure 5a)). Less amounts of water are drained and drainage is a little bit faster for the homogenous section. The comparison of different heterogeneous sections shows that there is a variability in drained cumulative fluxes (Figure 5a) and Figure 5b)). Yet, despite these slight differences, there is not a great impact from the section’s heterogeneity on flux rate at the lower boundary conditions, meaning that fluxes during the drainage and water redistribution phases should not be greatly impacted by the heterogeneity of the deposit.
Finally, at surface and at the lower boundary, water pressure heads decrease for all sections, as the result of water drainage and redistribution in the profile. This decrease is slightly more pronounced for the case of the homogenous section. For heterogeneous section, water pressure head at surface decreases to a lesser extent; revealing an over-pressure at surface, in comparison to the case of the homogeneous section. This over-pressure witnesses the increase in flow impedance for the heterogeneous section. This is logical and in agreement with the fact that heterogeneous profiles are made of the main material plus two materials with lower saturated hydraulic conductivity [25] [26] .
3.3. Modeling water Infiltration during Rainfall
Water infiltration was modeled for a particular rainfall event, considering atmospheric condition applied at surface boundary with a flux of 0.3438 m/h, which corresponds to a rainfall intensity of 6 mm/h, relating to a period of intense rain. The analysis of water content profiles gives information on the flow pathways during infiltration. For the homogeneous profile, wetting fronts correspond to horizontal lines, revealing a piston type infiltration (data not shown). Water infiltrates progressively with similar fluxes at a fixed depth. In the case of heterogeneous sections, the wetting fronts are no longer horizontal. During infiltration, for times between 0 and ~3 h, the wetting fronts strongly depend on the geometry of inclusions (Figure 6). For Section S1, water infiltrates in the medium of the section between the inclusions (Figure 6, A). For Section S3, water infiltrates mainly on the
Figure 5. Water redistribution during drainage phase: a) total cumulative flux drained at lower boundary, i.e., at a depth of 4 m, b) water flux at the lower boundary, water pressure heads at surface c) and at lower boundary d).
Figure 6. Time evolution of water contents in three sections during the studied rainfall event.
right side, apart from sand inclusions (Figure 6, B). And finally, for the more complicated Section S5, there is no specific preferential flow since inclusions are spread over the whole length of the profile (Figure 6, C). But, locally, water avoids inclusions. At the end of infiltration, when the wetting fronts have reached the lower boundary, water content differs between the main lithofacies and the inclusions. The sand lenses exhibit higher water content (Figure 6, D, D' and D'') because of their high saturated water content (Table 1). Above the edges of sand lenses, water content is increased (Figure 6, E, E' and E''). This results from the local increase in pressure head at the interfaces between sand lenses and the main material, above sand lenses. Such an increase reveals a drop in hydraulic conductivity from the main material to the sand. In fact, under these conditions, the sand lenses exhibit a lower hydraulic conductivity and force water to avoid them and triggers the increase in water pressure head. This increase above sand lenses can be regarded as similar in process to the formation of a perched aquifer [26] . Such results are in agreement with the previous works [3] . The contribution of this study is to show that depending on the section considered and the related sedimentological heterogeneity, flow pathways may change.
Soil heterogeneity affects flow pathways but also water infiltration at surface. For water pressure head, the influence is quite small (Figure 7c)). All water pressure heads tend towards zero and the difference between the homogeneous and the heterogeneous sections is quite tiny. For fluxes, the heterogeneity impedes flow rate and reduces water infiltration. In the homogeneous section, the whole water flux applied at surface is infiltrated and the water flux entering the profile equals the flux imposed (Figure 7a)). For the other sections, the water flux imposed at surface is completely infiltrated during one hour before being reduced, leading to a decrease in infiltration rate as depicted in Figure 7a). Sorting sections as a function of infiltrated fluxes leads to: H > S3 > S2 > S1 > S4 » S5. Such ranking will be discussed below in light of the following results.
At a depth of 4 m (i.e., lower boundary), both water fluxes and water pressure heads are impacted. For the homogeneous section, water pressure head and fluxes suddenly increase around 2 h. This time corresponds to the time needed for the wetting front to reach the lower boundary. It can be stated that, for the homogeneous section, the wetting front is sharp as witnessed by the sudden and drastic increase in both water pressure and
Figure 7. Water infiltration during rainfall event: fluxes at surface a) and at the lower boundary, i.e., at 4 m depth b); water pressure heads at surface c) and at lower boundary d).
flux rates. At the end, the whole profile is saturated with pressure heads close to zero and the water infiltrates at the same flow rate along the whole profile (gravity driven saturated flow). The heterogeneity of the section impacts the arrival of the wetting front. These arrive slightly later, around 2.25/2.5 h and the increase of water pressure head and water flux rate is less sharp with more complex shapes (Figure 7b) and Figure 7d)). In fact, these more complex shapes reveal several arrivals corresponding to several different pathways. In this case, the complexity of flow pathways due to profile heterogeneity impacts significantly the fluxes, including the fluxes that occur at every depth in the profile. Once the wetting front has reached the lower boundary, water pressure head increases up to zero as for the upper boundary, leading to full saturation along the whole profile. The water flux at the lower boundary tends towards the actual infiltration rate at the upper boundary. For instance, the water flux at the lower boundary of Section S4 is around 8.8 m3 h−1, corresponding to the water flux that infiltrate sat surface for an applied water flux of 10.3 m3 h−1. Regarding the sorting of arrival times, we obtain respectively the following rankings: S3 < S2 < S1 = S4 < S5. We obtain a ranking similar to that of infiltration rates, meaning that the section in which water infiltrates the less at surface corresponds to the slowest velocity of water and wetting fronts in the profile. Regarding time dispersion around averaged arrival times, the ranking changes without any link between arrival time and time dispersion. Indeed, some sections exhibit short arrival time with low dispersion (Section S2), others exhibit longer arrival time with large dispersion, etc.
Briefly, the heterogeneity of soil profile impacts significantly flow pathways and water infiltration and runoff at surface. In the studied profiles, the upper layer and the inclusions impede flow, resulting in more runoff at surface and slower movement of wetting fronts. In addition, these trigger the establishment of several flow pathways, resulting in the succession of several arrivals for the wetting front at a fixed depth. These results show that the heterogeneity of soil may significantly impact water redistribution or infiltration during both drainage and rainfall events. The following section addresses the effect of soil heterogeneity for a complete meteorological chronic.
3.4. Modeling water Infiltration for Meteorological data
A complete meteorological data was modeled for the several sections and for the first 1000 h of year 2008. Figure 8 presents water pressure head and cumulative flux at surface and at the lower boundary (Figures 8a)-d)). Figure 8 depicts also the water fluxes at boundaries for a specific rainfall event (Figures 8e)-f)). The meteorological
Figure 8. Numerical results for the meteorological chronic, potential flux at surface (a) or b)), water pressure heads at surface a) and at lower boundary, i.e., at a depth of 4m b), real cumulative fluxes at surface c) and at lower boundary d), zoom on a rainfall event depicting flux at surface e) and at lower boundary f).
data corresponds to the succession of rainfall events and drainage phases (dry periods) in between, measured at the meteorological station of Bron in Lyon urban areas.
For all sections, rainfall events logically trigger a quick increase in water pressure head and drainage triggers a slower decrease in water pressure head. It can be noted that time evolution of pressure head is wider at surface with values between −3 m and 0 m (Figure 8a)), whereas at the lower boundary the water pressure head varies between −1.5 and zero (Figure 8b)). This is often observed in most cases [27] . The soil can be seen as a buffer and variations in hydric conditions are often wider at surface than in deeper horizons. The differences between the homogeneous section and the heterogeneous sections are in agreement with what was described above for case studies. The heterogeneity impacts surface water pressure heads more during drainage phases than during rainfall events (Figure 8a)), as already stated above. The same trends are observed for water pressure head at lower boundary level.
For water fluxes, only cumulative fluxes were reported in Figure 8c) and Figure 8d) for the sake of clarity. Every rainfall event logically triggers a sharp increase in cumulative infiltration, whereas the drainage corresponds to plateaus. It can be noted that the shapes are sharper for cumulative infiltrations at surface (Figure 8c)) in comparison with the lower boundary (Figure 8d)). This results from the buffer effect of the soil and the fact that processes responsible for water movement in the soil smoothen the variation of fluxes and water pressure heads in deeper horizons. The difference between all the sections is extremely tiny before 250 min. After, the sections split into several groups with a clear distinction between the homogeneous and the heterogeneous sections. As observed in the previous chapter, the homogeneous section infiltrates more water than the others. This becomes clear when analyzing one specific event (Figure 8e) and Figure 8f)). For this event occurring between 260 min and 270 min, water infiltration at surface is the most important in the homogeneous section. For all the heterogeneous sections, water infiltration decreases, and sections can be sorted as a function of infiltrated fluxes as follows: H > S3> S2 > S1 » S4 > S5, which corresponds to the ranking obtained above for case study of rainfall event. Clearly, the behavior of each section in terms of water pressure head and fluxes corresponds to the same behavior as described above for a particular drainage and rainfall event, and the same conclusions can be stated.
At the end of the chronic, the combination of similar effects for all events leads to significant effect on the water budget. For instance, profile heterogeneity impacts the percentage of cumulative fluxes that was infiltrated at surface and that achieved infiltration to the lower boundary (positioned at a depth of 4 m). For the case of the homogeneous section, 95.2% of the water infiltrates into the profile with only 4.6% as runoff. The heterogeneity simultaneously increases runoff and decreases water infiltration. The ranking of sections leads to: H < S3 < S2 < S1 < S4 < S5 with a maximum value for runoff at 17.7% and a minimum value of runoff at 11.6%, for heterogeneous sections. Such a ranking is in full agreement with the previous analysis of case studies. Clearly, soil heterogeneity impacts runoff at surface but it can also be concluded also that depending upon the location of sections in the field and the geometry of inclusions, runoff may change significantly, as already proved [25] [26] even for this kind of deposit [3] [4] . But this study clearly shows that for the same deposit, soil heterogeneity may vary and flow pattern may vary as well. It is then crucial to account for spatial variability of the profile heterogeneity at the basin scale.
3.5. Link between flow and Geometrical indicators of heterogeneous Sections
In the previous sections, it was clearly demonstrated that the comparison of sections gave the same results for all drainage and rainfall events and over a chronic of 1000 h. It was shown that heterogeneity affected flow in the same way, but that the degree of heterogeneity of the profile plays on the intensity of the effect of soil heterogeneity. As a consequence, characterizing sedimentological properties for only one section and modeling unsaturated flow for a sole section is not sufficient for flow rate prediction at the infiltration basin scale. In this section, we assess the link between the impact of heterogeneity on flow and the values of indicators. As the influence of profile heterogeneity on flow pattern remains the same, whatever the drainage or rainfall event, we need only to study the link between flow and indicators for one case. Indeed, similar trends will be found for any other rainfall event or even for the meteorological chronic.
In this part, we assess the link between geometrical indicators and runoff at surface obtained for the complete meteorological chronic. In terms of runoff at surface, we obtain the following ranking: H < S3 < S2 < S1 < S4 < S5. Here, we deal with the effect of soil heterogeneity on flow impedance. At first, we test the indicator FLa, which corresponds approximately to the thickness of the upper layer. Indeed, physically, if we consider that the lower saturated hydraulic conductivity of the upper layer is one of the main key factors for flow impedance, we should get a clear link between the ranking of sections with regards to runoff and to FLa. Yet, these rankings do not correspond. The ranking with regards to FLa gives: H < S4 < S3 < S1 < S2 < S5; which is quite different. As a second step, we consider that the sand lenses are one of the main key factors for flow impedance. We sorted the sections as a function of the degree of occupation of the section by the sand lenses, i.e., indicator FLe. The ranking obtained with FLe was quite different to that of the runoff (Table 3). The procedure was repeated to all indicators and no clear concordance was found (Table 3). Briefly, there is no link between runoff and one particular indicator. This shows that flow may be more the result of a combination of several indicators. Clearly, more data for more sections are needed to identify the combination of proposed parameters that explain results related to flow. Regarding the physics of flow, the worse situation for water infiltration corresponds to the section for which the upper layer is thick and sand lenses occupy a large fraction of the section and are spread all over the section length. For instance, Section S5, which fulfills this criterion, triggers the smallest runoff and corresponds to the strongest effect of heterogeneity on flow.
Table 3. Ranking of section with regards to runoff for the meteorological data (Flow) and with regards proposed geometrical indicators (FLa, FLe, XGC, IDC, IDCL, and Lmax).
4. Conclusion
In this study, we examined the effect of soil heterogeneity on unsaturated flow processes. Numerical modeling was employed to model unsaturated flow for different events (drainage phase, rainfall event and a succession of rainfall and drainage events for a complete meteorological chronic) in 5 different real sections and a hypothetic homogeneous section filled with the main lithofacies (blank). These sections were previously properly character- rized with regard to their sedimentological properties (architecture and lithofacies) using GPR and then modeled in terms of flow. It was proved that the upper layer and sand inclusions impeded flow at the section scale, reducing water movement into the soils and increasing water runoff at surface. Locally, the inclusion of sand lenses modified flow pathways, forcing the water to pass through pathways among inclusions. These effects were due to their lower hydraulic conductivity. In addition, the upper layer and sand lenses increased accumulation of water in the profile due to their higher saturated water content. One of the main conclusions of this study is that if all heterogeneous sections differ from those of the homogeneous section, the variability among heterogeneous sections is also significant. Clearly, a sole section is not representative of all sections and several sections must be investigated if flow needs to be investigated at the scale of the whole infiltration basin. Thus, we tried to propose geometrical indicators to explain and potentially predict flow pattern. However, the results show that the link between these indicators and modeled flow is not direct and that a combination of indicators rather than a sole indicator should be identified for the prediction of flow. Additional data are required to properly define and identify the right combination of factors, which is the subject of ongoing research. Finally, this paper clearly demonstrates the influence of soil heterogeneity on flow pathways, which is essential for understanding pollutant transport by water and access to the reactive particles of soils [9] [10] . This gives pertinent information for the modeling and understanding of the fate of pollutants in such a deposit and in infiltration basins that rest on this kind of deposit.
Acknowledgements
The first author received a Ph.D. scholarship from the projects CAPES/COFECUB and FACEPE. The authors are grateful to the OTHU, Greater Lyon and the ANR-GESSOL program (FAFF project: Filtration Function of an Urban Structure―Consequence on the Formation of an Anthroposol) for their logistic and financial support.
Cite this paper
Artur PaivaCoutinho,LaurentLassabatere,ThierryWiniarski,Jaime Joaquim da Silva PereiraCabral,Antonio Celso DantasAntonino,RafaelAngulo-Jaramillo, (2015) Vadose Zone Heterogeneity Effect on Unsaturated Water Flow Modeling at Meso-Scale。 Journal of Water Resource and Protection,07,353-368. doi: 10.4236/jwarp.2015.74028
References
- 1. Mikkelsen, P.S., Hafliger, M., Mikkelsen, P.S., Hafliger, M., Ochs, M., Jacobsen, P., Tjell, J. C. and Boller, M. (1997) Pollution of Soil and Groundwater from Infiltration of Highly Contaminated Stormwater—A Case Study. Water Science and Technology, 36, 325-330.
http://dx.doi.org/10.1016/S0273-1223(97)00578-7 - 2. Goutaland, D. (2008) Caracterisation hydrogeophysique d’un depot fluvioglaciaire. Evaluation de l’effet de l’heterogeneite hydrodynamique sur les ecoulements en zone non-saturee. Ph.D. Thesis, Graduate School of Chemistry, University of Lyon, 241 p.
- 3. Goutaland, D., Winiarski, T., Lassabatere, L., Dube, J.S. and Angulo-Jaramillo, R. (2013) Sedimentary and Hydraulic Characterization of a Heterogeneous Glaciofluvial Deposit: Application to the Modeling of Unsaturated Flow. Engineering Geology, 166, 127-139.
http://dx.doi.org/10.1016/j.enggeo.2013.09.006 - 4. Winiarski, T., Lassabatere, L., Angulo-Jaramillo, R. and Goutaland, D. (2013) Characterization of the Heterogeneous Flow and Pollutant Transfer in the Unsaturated Zone in the Fluvio-glacial Deposit. Procedia Environmental Sciences, 19, 955-964.
http://dx.doi.org/10.1016/j.proenv.2013.06.105 - 5. Leclerc, R.J. and Hickm, E.J. (1997) The Internal Structure of Scrolled Floodplain Deposits Based on Ground-Penetrating Radar, North Thompson River, British Columbia. Geomorphology, 21, 17-38.
http://dx.doi.org/10.1016/S0169-555X(97)00037-8 - 6. Mumphy, A.J., Jol, H.M., Kean, W.F. and Isbell, J.L. (2007) Architecture and Sedimentology of an Active Braid Bar in the Wisconsin River Based on 3-D Ground Penetrating Radar. Special Paper of the Geological Society of America, 432, 111-131.
- 7. Lunt, I.A., Bridge, J.S. and Tye, R.S. (2004) A Quantitative Three-Dimensional Depositional Model of Gravelly Braided Rivers. Sedimentology, 51, 377-414.
http://dx.doi.org/10.1111/j.1365-3091.2004.00627.x - 8. Lassabatere, L., Angulo-Jaramillo, R., Soria Ugalde, J.M., Cuenca, R., Braud, I. and Haverkamp, R. (2006) Beerkan Estimation of Soil Transfer Parameters through Infiltration Experiments—BEST. Soil Science Society of America Journal, 70, 521-532.
- 9. Lassabatere, L., Winiarski, T. and Galvez Cloutier, R. (2004) Retention of Three Heavy Metals (Zn, Pb, and Cd) in a Calcareous Soil Controlled by the Modification of Flow with Geotextiles. Environmental Science and Technology, 38, 4215-4221.
http://dx.doi.org/10.1021/es035029s - 10. Lamy, E., Lassabatere, L., Bechet, B. and Andrieu, H. (2009) Modeling the Influence of an Artificial Macropore in Sandy Columns on Flow and Solute Transfer. Journal of Hydrology, 376, 392-402.
- 11. Kohne, J.M., Kohne, S. and Simunek, J. (2009) A Review of Model Applications for Structured Soils: b) Pesticide Transport. Journal of Contaminant Hydrology, 104, 36-60.
http://dx.doi.org/10.1016/j.jconhyd.2008.10.003 - 12. BURGEAP (1995) Study of the Water Table of the Eastern Part of Lyon Area. (In French) Le Grand Lyon Direction de l’eau, Lyon.
- 13. Huggenberger, P., Meier, E. and Pugin, A. (1994) Ground-Probing Radar as a Tool for Heterogeneity Estimation in Gravel Deposits: Advances in Data-Processing and Facies Analysis. Journal of Applied Geophysics, 31, 171-184.
http://dx.doi.org/10.1016/0926-9851(94)90056-6 - 14. Beres, M., Huggenberger, P., Green, A.G. and Horstmeyer, H. (1999) Using Two- and Three-Dimensional Georadar Methods to Characterize Glaciofluvial Architecture. Sedimentary Geology, 129, 1-24.
http://dx.doi.org/10.1016/S0037-0738(99)00053-6 - 15. Bridge, J.S. and Lunt, I.A. (2006) Depositional Models of Braided Rivers. In: Sambrook-Smith, G.H., Best, J.L., Bristow, C.S. and Petts, G.E., Eds., Braided Rivers: Process, Deposits, Ecology and Management, Blackwell Publishing, Oxford, 11-49.
http://dx.doi.org/10.1002/9781444304374.ch2 - 16. Schrott, L. and Sass, O. (2008) Application of Field Geophysics in Geomorphology: Advances and Limitations Exemplified by Case Studies. Geomorphology, 93, 55-73.
http://dx.doi.org/10.1016/j.geomorph.2006.12.024 - 17. Miall, A.D. (1999) Principles of Sedimentary Basin Analysis. 3rd Updated and Enlarged Edition, Springer, Berlin.
- 18. Goutaland, D., Winiarski, T., Dube, J.S., Bievre, G., Buoncristiani, J.F., Chouteau, M. and Giroux, B. (2008) Hydrostratigraphic Characterization of Glaciofluvial Deposits Underlying an Infiltration Basin Using Ground Penetrating Radar. Vadose Zone Journal, 7, 194-207.
http://dx.doi.org/10.2136/vzj2007.0003 - 19. Goutaland, D., Winiarski, T., Bièvre, G. and Buoncristiani, J-F. (2005) Interêt de l’approche sedimentologique en matière d’infiltration d’eaux pluviales. Caracterisation par radar geologique. Techniques Sciences Methodes, 10, 71-79.
- 20. Mitchum, R.M.J., Vail, P.R. and Sangree, J.B. (1977) Stratigraphic Interpretation of Seismic Reflection Patterns in Depositional Sequences. In: Payton, C.E., Ed., Seismic Stratigraphy: Applications to Hydrocarbon Exploration, the American Association of Petroleum Geologist, Tulsa, Vol. 26, 117-133.
- 21. Simunek, J. and van Genuchten, M.T. (2008) Modeling Nonequilibrium Flow and Transport Processes Using Hydrus Version 4.0. HYDRUS 1D. Department of Environmental Sciences, University of California, Riverside.
- 22. van Genuchten, M.T. (1980) A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Science Society of America Journal, 44, 892-898.
http://dx.doi.org/10.2136/sssaj1980.03615995004400050002x - 23. Lassabatere, L., Angulo-Jaramillo, R., Goutaland, D., Letellier, L., Gaudet, J-P., Winiarski, T. and Delolme, C. (2010) Effect of the Settlement of Sediments on Water Infiltration in Two Urban Infiltration Basins. Geoderma, 156, 316-325.
http://dx.doi.org/10.1016/j.geoderma.2010.02.031 - 24. Heinz, J., Kleineidam, S., Teutsch, G. and Aigner, T. (2003) Heterogeneity Patterns of Quaternary Glaciofluvial Gravel Bodies (SW-Germany): Application to Hydrogeology. Sedimentary Geology, 158, 1-23.
http://dx.doi.org/10.1016/S0037-0738(02)00239-7 - 25. Birkholzer, J. and Tsang, C.F. (1997) Solute Channeling in Unsaturated Heterogeneous Porous Media. Water Resources Research, 33, 2221-2238.
http://dx.doi.org/10.1029/97WR01209 - 26. Miyazaki, T. (2006) Water Flow in Soils. CRC Press, Boca Raton.
- 27. Kutilek, M. and Nielsen, D.R. (1994) Soil Hydrology. Catena Verlag, Cremlingen.










