Journal of Water Resource and Protection
Vol.06 No.15(2014), Article ID:51682,6 pages
10.4236/jwarp.2014.615132
Synthetic Reconstruction of Water Demand Time Series for Real Time Demand Forecasting
Bruno M. Brentan1, Lubienska C. L. J. Ribeiro2, Edevar Luvizotto Jr.1, Danilo C. Mendonça2, José M. Guidi3
1Water Recourses Department, School of Civil Engineering, Unicamp, Campinas, Brazil
2School of Technology, Unicamp, Limeira, Brazil
3Company of Water Supply of São Paulo, Franca, Brazil
Email: brunocivil08@gmail.com, lubi@ft.unicamp.br, josemguidi@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 September 2014; revised 8 October 2014; accepted 2 November 2014
ABSTRACT
The forecasting of the demand applied to water supply systems has been an important tool to realize time control. The use of the time series to do the forecasting of the demand is the main way that has been used by researchers. By this way, the need of a complete time demand series increases. This work presents two ways to reconstruct the water demand time series synthetically, using the Average Reconstruction Method and Fourier Method. Both the methods were considered interesting to do the synthetic reconstruction and able to complete the time series, but the Fourier Method showed better results and a better fitness to approximation of the water consumption pattern.
Keywords:
Water Demand Forecasting, Synthetic Reconstruction, Water Supply Systems

1. Introduction
The increase of the demand on the urban water supply systems and the need of accuracy on the control of these systems require an increase at the precision of the forecasting of the water demand. According to [1] , this activity in water supply systems becomes an essential tool for the design, operation, and management. The activities of operation and management of these systems require a short-term demand forecasting because these activities are done at real time or near real time and this control needed more information of the demand to supply the consumers with more quality and safety.
The short term forecasting can be done by the analysis of measured time series of consumption at the sector that is being controlled and managed, and the time demand series can be obtained by the measurement of water flow at consumption points or outflow of reservoirs or tanks for example.
Sometimes, these measurements are done by electronic apparatus which are subject to troubles such as electrical fail or data storage that jeopardize the data consistency and can harm the temporal series analysis.
Several methods to forecasting the water consumption have been proposed by researchers. [2] - [5] mostly use temporal series analysis and cross-relation. But a few works have been proposed to treat the problem of the synthetic complete of these series. To complete the fails occurred during the measurement of the demand data, this work proposes two methods: one based on daily average and monthly averages, another based on Fourier Series.
2. The Demand Analysis
If a time series of water demand is observed, it is possible to see a periodic oscillation on the consumption of water. Furthermore, if the sector that is being managed is a residential sector, the oscillation is more known, because the consumption of water at a residential sector is widely studied. So it is possible to confirm that this oscillation will be repeated with a few variations at the values in a week [6] .
Another observation that is possible to do: the behavior of the demand follows a pattern according the day of the week. By this way, if a value of the demand is known at one time of one weekday, it’s expected a repeat of any value near of the known demand. The deviation of the expected demand can be justified because the value of the demand is affected by the weather factors such as rain, temperature variation, relative humidity [7] .
For this work, the analysis of the water demand was done using a real time series obtained with a measurement of the consumption of water in a residential urban sector at Franca, a city of the state of São Paulo, Brazil. The measurement was done for 26 months every 20 minutes of all days.
The graphic at Figure 1 and Figure 2 can illustrate the behavior of the water demand at 24 hours for 5 days. The first shows the variation for 5 days at the same week and the second graphic shows the variation of the demand for the 5 same weekdays. At this work, the determination of the observation period of the water demand behavior was done with the analysis of a day that will be used for a validation of the purposed methods. Taking this day as a d-day, it is possible to take two days after and two days next with them measured demands and plotting these demands, it is possible to obtain the follow curves. These figures can help the analysis of the variation of the demand, confirming the repetition of the pattern of consumption said above.
At Figure 1, it is possible to observe a bigger variation of the demand among the days. The main information that the week of the analyzed day is the local variation of the demand by the weather factors. Looking for the week, it is possible to see the increase or decrease of the demand.
Figure 2 confirms the idea of the correlated behavior of the demand with the weekday. Take this information can be important to determine the reconstruction of the water time series because the pattern of the demand is repeated at a weekday.
3. Average Reconstruction Method
The method of Averaged Reconstruction was developed based on the methods of synthetic reconstruction of rain time series and considering the demand variation showed above. The method uses the week pattern of consumption and the weekday pattern of consumption. With the measured demand of the two days after the analyzed day and two days next, it is possible to calculate the average consumption for each day and with this value, for each time of measurement, it is possible to determine a factor f1, which means the deviation between the demand of each measurement time and the average value.
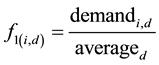 (1)
(1)
where  is the week factor for day d to time-measurement i.
is the week factor for day d to time-measurement i. 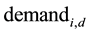 is the water demand measured at day d, at time i. And
is the water demand measured at day d, at time i. And 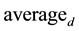 is the average water consumption for day d.
is the average water consumption for day d.
After, it is possible to calculate the average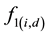 , called
, called , and with this value, multiplying by the average demand it is possible to obtain an estimated value
, and with this value, multiplying by the average demand it is possible to obtain an estimated value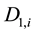 , the demand for each time of measurement i.
, the demand for each time of measurement i.
Figure 1. Daily variation of water consumption in a week (considering 5 days).
Figure 2. Week daily variation of water consumption for a Tuesday.
After the calculation of the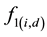 , it can take two weekday ago and two weekday after the analyzed day that it wants to reconstruct the time series. Doing the same process to calculate
, it can take two weekday ago and two weekday after the analyzed day that it wants to reconstruct the time series. Doing the same process to calculate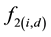 , it can obtain another estimated value
, it can obtain another estimated value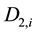 .
.
So is possible to compose a final demand 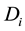 with
with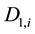 , and demand
, and demand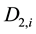 , as follow:
, as follow:
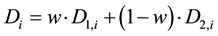 (2)
(2)
where Di is the reconstructed water demand for the time i and w is the weight of the demand
With the value of the demand Di, it is possible to calculate the error E according the Equation (3):

where 
The value of w is determined by a minimization of E, which shows the factor most important at composition of the final demand using the solver of the MS Excel 2007®.
To validate this method, the work purposes a reconstruction of two days that was full measured and by this way evaluate the final value of E. Table 1 shows the value of the function E for the two tested days.
Considering the method of the calculation the demand D1 (Week average) and D2 (Weekday average) the Figure 3 and Figure 4 above show the behavior of these reconstructed demands and the final demand D.
It is possible to observe the method can do a good reconstruction of the time series but it is not able to reproduce the big variation of the demand all day along as observed at time 35 (Figure 3) or 55 (Figure 4).
4. Fourier Series Method
Knowing the repetition of the oscillation on the demand, this second method purposes the use of the Fourier series to reconstruct the time series of the water demand. The method uses a combination of sine and cosine those will be approximate the function to the measured data. The application of the Fourier series was inspired on the work of [8] that applies this method to model the behavior of the electrical residential demand, as well the water demand has a typical oscillation all day along.
The demand Di can be written as:

The index j corresponds to the number of the terms of Fourier series. At this work, as showed at Figure 5 and Figure 6, the number of terms was chosen as four because, like it is possible to observe at figures, there is a few
Table 1. Squatter error of the averaged method applied for two days.
Figure 3. Behavior of the reconstructed demand for day 06/05/2012.
Figure 4. Behavior of the reconstructed demand for day 06/05/2012.
Figure 5. Behavior of the reconstructed demand for day 06/05/2012?Fourier Method.
improvements on the capacity of reproduction of the time series when the number of terms is changed of 3 for 4 terms (value of j). The value of xi can be obtained doing a transformation with the value i, the time of measurement, according the Equation (9).
According to [9] , it is possible to determine the coefficients of the Fourier series as follow:

Figure 6. Behavior of the reconstructed demand for day 07/28/2012.
Table 2. Squatter error of the Fourier Method applied for two days.



where 
The Fourier Method was more effective to reconstruct the time series of water demand. Besides the reduction of the squatter error, the graphic shows the less deviation at the shape of the behavior of the demand. The capacity of this method to represent de oscillation of the demand can justify the better results.
5. Conclusions
The forecasting of demand, mainly the short term forecasting has been more important to definition of the operation at real time on the water-supply systems. The measurement of the demand to generation of a forecasting model, sometimes, has any fails that can give troubles to determine a reliable model. By this way, this work purposed two methods to do a synthetic reconstruction of water demand time series.
At first, the Averaged Reconstruction Method, whose fitness could be considered acceptable, though for some times, it is possible to observe a significant deviation between the measured data and the synthetic data. This deviation is observed because the technique was not able to complete all time series along. By Figure 3 and Figure 4 it is also possible to observe the improvement at fitness using the composition of the final demand by the reduction of this deviation.
The second method, Fourier Series Method, was able to determine with more accuracy the behavior of the demand all day along. The advantage of the Fourier method is the reduction of the deviation between the reconstructed demand and the measurement. But also this method was not able to reproduce the extreme variation of the demand some times of the day.
All methods can be applied to compose the study of the time series of the demand. Maybe the Fourier Method can be more efficient to define the unknown demands and can give more reliable forecasting model.
References
- Herrera, M., Torgo, L., Izqueirdo, J. and Pérez-Garcia, R. (2010) Predictive Models for Forecasting Hourly Urban Water Demand. Journal of Hidrology, 387, 141-150. http://dx.doi.org/10.1016/j.jhydrol.2010.04.005
- Adamowski, J. (2008) Peak Daily Water Demand Forecast Modeling Using Artificial Neural Networks. Journal of Water Resources Planning and Management, 134, 119-128. http://dx.doi.org/10.1061/(ASCE)0733-9496(2008)134:2(119)
- Perry, P.F. (1981) Demand Forecasting in Water Supply Systems. Journal of the Hydraulics Division, 107, 1077-1087.
- Santos, C.C. (2011) Forecast of Water Demand in the Metropolitan Region of San Paul with Artificial Neural Networks and Socio-Environmental and Weather Conditions. Doctor Theses, EPUSP, San Paul.
- Silva, C.S. (2003) Multivariate Forecast of Water Demand in Urban Water Supply Systems. Previsão multivariada de demanda de água em sistemas urbanos de abastecimento. Doctor Theses, Unicamp, Campinas.
- An, A., Shan, C.C., Cercone, N. and Ziarko, W. (1995) Discovering Rules from Data for Water Demand Prediction. Proceedings in the Workshop on Machine Learning and Expert System (IJCAI’95), 187-202.
- Lucas, S.A., Coombes, P.J. and Sharma, A.K. (2010) The Impact of Diurnal Water Use Patterns, Demand Management and Rainwater Tanks on Water Supply Network Design. Water Science & Technology: Water Supply―WSTWS, 10, 69-80.
- Magnano, L. and Boland, J.W. (2007) Generation of Synthetic Sequences of Electricity Demand. Application at South Australia. Energy, 32, 2230-2243. http://dx.doi.org/10.1016/j.energy.2007.04.001
- Luvizotto, E.J. (1992) Analytical Representation of Characteristic Curves of Hydraulic Machines for Use in Computer Simulations routines. MSc. Thesis, EPUSP, San Paul.








