Journal of Water Resource and Protection
Vol.6 No.9(2014), Article
ID:47399,11
pages
DOI:10.4236/jwarp.2014.69081
Measuring Autogenic Recharge over a Karst Aquifer Utilizing Eddy Covariance Evapotranspiration
Nico M. Hauwert1, John M. Sharp2
1City of Austin Watershed Protection Department, Austin, USA
2Jackson School of Geosciences, University of Texas at Austin, Austin, USA
Email: nico.hauwert@austintexas.gov, jmsharp@jsg.utexas.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 March 2014; revised 5 April 2014; accepted 29 April 2014
Abstract
Autogenic, or direct aquifer recharge can best be measured as the remainder of a water balance utilizing precise measurement of precipitation, evapotranspiration (ET) and runoff. ET is the largest component of a precipitation water balance and can be measured within 5% using an eddy covariance system with Bowen-ratio energy balance corrections. Water balance components of precipitation, evapotranspiration, internal runoff, soil moisture were measured using a eddy covariance system, tipping bucket and visual rain gauges, flumes, and soil-moisture sensors. The research site was located within a 0.19-km2 (46-acre) internal drainage sinkhole basin where runoff never flows beyond the basin, but potentially reaches a cave serving as a drain to the sinkhole. Other than the cave drain, the basin slopes are indistinguishable from other slopes across the Barton Springs Segment of the Edwards Aquifer. Over a 505-day water balance interval where change in soil moisture was negligible and precipitation was 42% above average, ET was 68% of precipitation, discrete internal runoff was 6%, and remaining component of diffuse autogenic recharge was measured as the residual of total rainfall as 26% of rainfall. Over a longer period of average rainfall, internal runoff diminished to 3%, but was as high as 42% of precipitation during single storms when the soils were near saturation. These results closely match results from a fiveyear water balance over the Trinity Aquifer of Central Texas where ET was measured to be 65% of precipitation using a Bowen-ratio climate tower, runoff was measured to be 5% of precipitation, and recharge was calculated as the residual at 30% of rainfall. ET flux tower data from other sites across Central Texas indicate that under average precipitation conditions, autogenic recharge is about 28% and intervening recharge area runoff is about 3% of precipitation. During years of higher than average precipitation, authogenic recharge and intervening recharge area runoff combined increase within the range of 30% to 45% of precipitation.
Keywords
Evapotranspiration, Recharge, Edwards Aquifer, Karst, Water Balance

1. Introduction
In order to preserve increasingly scarce water supplies, understanding of recharge processes is vital. Recharge occurs below the surface where it is difficult or impossible to directly observe and measure. Recharge can be measured indirectly by accurately accounting for water balance components of precipitation or stream-flow loss.
Karst is a landscape underlain by soluble rock that typically contains large, focused springs and solution features such as caves, sinkholes, and sinking streams. Karst aquifers, such as the Edwards Aquifer, are some of the most productive water resources in the world. The rainfall to recharge cycle involves several steps including:
1) Evaporation of water on the surface, atmosphere, and plant surfaces (interception)2) Infiltration of rainfall and runoff into the soils, a portion of which is utilized by plants within their growing structure or is released to the atmosphere as evaporation and transpiration or interflow which repeats the runoff cycle3) Percolation of a portion of infiltrated water into the bedrock and unsaturated zone, a portion of which may be temporarily stored over in perched pools or matrix4) Recharge of percolated water into the water table of the aquifer.
Components of natural surface recharge of a karst area include:
1) Allogenic recharge originating as flow from upstream source areas percolating within the major creek channels2) Autogenic (also authogenic and direct) recharge originating from direct precipitation over the recharge area of the karst aquifer.
a) Diffuse recharge that infiltrates through soil and small solution features and percolate into the bedrock of the intervening recharge area.
b) Discrete internal runoff (also internal drainage) recharge where runoff directly percolates into the bedrock of the intervening recharge area, typically through solution-enlarged sinkhole drains.
c) Major creek channel autogenic recharge is runoff originating as precipitation over the recharge area of a karst aquifer that percolates into swallets and other recharge features of the major creek channels.
3) Other natural leakage recharge sources potentially include leakage through overlying confining units or adjacent aquifers.
The amount of precipitation that recharges an aquifer, or recharge rate, is typically expressed as a percent or fraction of precipitation and is commonly measured using stream-flow loss, spring-flow hydrographs, isotopes, and chloride concentrations. The accuracy of recharge rate measurement from stream-flow loss depends on the accuracy of discharge measurements and precise delineation of groundwater basins contributing to spring discharge under varying hydrologic conditions. Recharge rate measurement using chloride assumes sufficiently precise characterization of average chloride concentrations in rainfall and groundwater and the assumption that significant chloride concentrations solely originate from rainfall—an assumption that is difficult to insure in modern marine settings and in rocks deposited in past marine settings [1] -[5] . In addition, the addition of a small percent of highly concentrated chemical or isotopic composition, such as a brine or leakage from an adjacent aquifer may be misinterpreted to indicate that a karst aquifer has much older age than a volumetric averaged age of sources would indicate. In general, an incomplete understanding of a karst aquifer tends to result in a bias of underestimating the recharge rate [6] .
Studies utilizing a variety of methods across the world typically demonstrate that a relatively large portion of precipitation recharges karst aquifers [7] -[9] . A study of the Carboniferous Limestone in Mendip Hills, England found that no downstream runoff was generated and that 54% of precipitation recharged the aquifer [10] . Dublyanskii et al. [11] used stream flow loss to measure recharge amounting to 33% of precipitation in Crimea, Ukraine. In Guam, direct recharge amounted to 60% [12] to 67% [13] of precipitation. In Tunisia, Tixeront et al. [14] measured that 16% to 49% of annual precipitation recharged a Senonian monocline and two Jurassic limestone horsts over four years. Schoeller found that the recharge rate of a 5.8 km2 Tunisian Eocene limestone syncline groundwater basin to Kef Spring varied annually over eight years from 30% to 90% depending on the amount of precipitation, intensity of rainfall and groundwater-level conditions [15] . Over 19 km2 of the Djebel Bargou Aptial limestone syncline of Tunisia, Zebidi [16] measured 18% recharge rate over two years. Mero found that 53% of average precipitation recharged the 200 km2 Cretaceous limestone aquifer discharging from Na’aman Spring in Israel over 30 years [17] . Goldschmidt found that 10% to 45% of rainfall recharged karst limestone of West Galilee of Israel [18] . Mandel and Shiftan indicated that 37% of precipitation recharged a Turonian/Cenomanian limestone aquifer of Israel [19] . In the 5123 km2 Damascus basin of Syria, Burdon measured recharge as 41% of precipitation [20] . Voûte measured that 45% of precipitation recharged the Ghabbasin of Syria [21] . A recent study by Al-Charideh utilized the isotopic compositions of δ18O, δ2H, and chloride concentrations from 2001 to 2009 and found that 43% and 67% of precipitation recharged the Mountain karst aquifer and Figeh Spring of Damascus [22] . Hoetzl reports that in karst areas of Saudia Arabia, 47% of precipitation recharges [23] . In karst areas of Greece, Aronis et al. measured that an average of 52% of precipitation recharged a 95 km2 groundwater basin to the five main Lialaia Springs over 20 years [24] . Burdon and Papakis measured that 51% of precipitation recharged the adjacent Parnassos-Ghiona carbonate aquifer of Greece [25] .
The Edwards Aquifer consists of several segments, including the San Antonio Segment, the Barton Springs Segment, the Northern Segment, and aerially extensive Edwards Plateau. The relatively compact size of Barton Springs Segment provides a suitable study area of the Edwards Aquifer. The Barton Springs Segment has 241 km2 (94 mi2) recharge area containing outcrop of the Edwards Aquifer, eastern drainage areas where overlying confining units drain runoff back to the outcrop area, as well as isolated topographically high or down faulted blocks of overlying confining units. The recharge area of the Barton Springs Segment that discharges at Barton Springs is a smaller subset of the Barton Springs Segment, 212 km2 (82 mi2) [26] . After eliminating areas covered with Del Rio Clay and other overlying confining units, the Edwards Aquifer outcrop area contributing to Barton Springs is only 176 km2 (68 mi2). A 30 km2 (12 mi2) recharge area of the Barton Springs Segment provides discharge to Cold Springs [26] —a group of springs partially submerged below the Colorado River that cannot be directly gauged [27] . The recharge area can be further distinguished into major creek channels and intervening (upland) area between the major creek channels. A 680 km2 (264 mi2) contributing area, underlain primarily by rocks of the Trinity Group, provides an upstream catchment of allogenic recharge for the major creek channels crossing the Barton Springs Segment recharge area.
Recharge to Central Texas karst aquifers has also been reported. Prior to the 1970’s, because of the surface morphological characteristics and high transmissivity of the Edwards Aquifer, geologists assumed that a relatively high portion of rainfall recharged the aquifer [28] . Garza applied a flow loss water balance for the San Antonio Segment of the Edwards Aquifer that calculates potential recharge within a stream basin as the net difference in upstream and downstream gauging stations in addition to estimated runoff generated within the intervening area [29] . Slade et al. applied this method to estimate the amount of stream (85%) and intervening (15%) recharge to Barton Springs [30] , prior to delineation of groundwater basins using groundwater tracers that was later conducted. Using the Slade et al. (1986) results, Woodruff created a water balance to calculate that 85% of rainfall was lost through evapotranspiration, 5% of rainfall recharged in the major stream channels, and that 0.89% of rainfall recharged within the intervening upland areas [31] . The amount of rainfall attributed to direct recharge over the Edwards Aquifer (0.89%) was less than the 1% of rainfall that was estimated to percolate into the Eagle Ford Shale over a one-year interval in Central Texas [32] . Slade utilized the same presumed source areas and stream flow data from his earlier 1979 to 1983 study and determined that intervening areas contribute a maximum of 25% of total recharge and that this recharge constituted a maximum of 6.6% of precipitation using the same assumed groundwater basins [33] . Groundwater tracing conducted since 1996 has significantly refined groundwater basins contributing to Barton Springs [26] . Errors in groundwater basin delineation can account for the relatively low authogenic recharge to rainfall ratios calculated by the earlier recharge studies [26] .
Site specific water balances utilizing climate towers in Central Texas have more accurately measured evapotranspiration at site scale using eddy covariance or Bowen ratio systems along with weirs and flumes to measure surface runoff. Over a 5-year water balance of the Trinity Aquifer in Uvalde County, Dugas et al. used Bowenratio tower to calculate that 65% of rainfall evaporated or transpired, 5% of rainfall flowed as runoff into creeks, and 30% of rainfall recharged the underlying aquifer [34] . This study included two paired microbasins of Seco Creek, one of which was cleared of juniper, in order to examine the short-term effects of vegetation on the water budget. Based on Dugas et al. [34] results, Huang & Wilcox believed the recharge rate of the Edwards Aquifer must be greater than 10% of rainfall and that a stream-flow loss study in the same watershed significantly underestimated actual recharge [35] .
Slattery et al. reported rainfall and evapotranspiration on uplands adjacent to the Honey Creek tributary to the Guadalupe River using rain gauges and two Bowen-ratio climate towers [36] . The Honey Creek site is underlain by the Trinity Aquifer. Over 342 days, from March 19, 2002 to February 24, 2003, 1531 mm of precipitation and 632 mm of ET were measured, yielding an ET/precipitation ratio of 44%. Banda and Slattery later reported average values for 2002-2004 for two microbasins of ET as 78% and 81% of rainfall, runoff as 5% rainfall of rainfall, and a recharge rate as 14% and 17% of rainfall [37] . After clearing one microbasin of juniper, the untreated control averaged 85% ET, 2% runoff, and recharge rate of 13% of rainfall. Over the same six-year interval, the cleared microbasin had an ET rate of 74% of rainfall, runoff 2% of rainfall, and a recharge rate of 24% of rainfall [37] .
Heilman et al. reported five years of eddy covariance-measured evapotranspiration and rainfall over the Edwards Aquifer within the Blanco River watershed [38] . ET ranged from 57% to 112% of precipitation, averaging 76% of precipitation in the woodland station, and 79% of precipitation in the savanna station. ET values greater than 100% may be possible during years of low rainfall as moisture stored in drying soils and plants are released.
In this study, at site scale we measure the water balance components of rainfall, including runoff, soil moisture storage, and ET, to calculate recharge as the residual of precipitation. Each of the water balance components can be measured with high accuracy at site scale, consequently providing the most precise measurement of recharge. Site-specific ET and runoff data will then be compared with annualized data from other sites across Central Texas in order to provide recharge as a percent of rainfall under a range of precipitation conditions for the Edwards Aquifer.
2. Methodology
2.1. Study Area
Headquarters Flat Sinkhole Research station (HQ Flat) is a 0.19 km2 (46-acre) internal-drainage sinkhole basin located on the “J-17” City of Austin Water-Quality Protection Land within the Barton Springs Segment of the Edwards Aquifer (Figure 1).
Aside from the terminal runoff drain at HQ Flat Cave, the slopes of the basin are otherwise are indistinguishable from slopes outside the basin. About 10% of the recharge area for the Barton Springs Segment is contained within similar internal drainage microbasins, from which runoff rarely, if ever, flows to local creeks [26] .
2.2. Data Collection
Within a closed sinkhole basin of known area over a selected time interval, the amount of percolation into the bedrock can be calculated as:
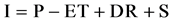 (1)
(1)
where:
P = precipitation volume (m3);
ET = evapotranspiration flux volume (m3);
I = percolation from soil and lesser karst features into the underlying bedrock (diffuse recharge, m3);
DR = internal runoff that enters the cave drain (discrete recharge, m3);
S = change in water storage in soil during the reference period (m3).
A 505-day period, from April 2, 2004, to August 20, 2005, was selected for determining the water balance where starting and ending volumetric soil moisture was measured to be 20% ± 2%. Because percolation occurs below the expected extinction depth beyond significant ET occurs, for the purposes of this study it is assumed that all percolated groundwater becomes recharge. The water table of the Edwards Aquifer is about 60 m (200 ft) deep at the research site.
Precipitation was measured using funnel cap plastic All-Weather rain gauges. These gauges have measurement precision of 0.0254 cm (0.01-inch) and are designed to reduce evaporative loss. In addition, three 0.0254 cm (0.01-inch) Rainwise tipping bucket rain gauges with HOBO data loggers continuously measured precipitation. Tipping-bucket rain gauges are prone to plugging from bird droppings and require careful maintenance. The Rainwise tipping buckets required a small calibration shift, based on verification with a graduated cylinder

Figure 1. Location of study site (HQ Flat sinkhole microbasin is the primary water balance research site. Comparison rainfall and runoff was measured in Flint Ridge sinkhole catchment).
as well as correlations among other stations and visual rain gauges. Monthly totals of rainfall were compared at all gauges to find and correct potential data gaps.
Flow is directed to HQ Flat Cave from 94% of its catchment area along a single channel which was outfitted with a 0.6 m (2 ft) aluminum H flume. An ISCO 3230 flow meter was used to continuously measure flow entering HQ Flat Cave. Outside of internal drainage basins this flow may be representative of runoff entering the major creeks. A second large internal drainage basin sinkhole, Flint Ridge (Figure 1), was also monitored for flow within its three terminal drainages in order to evaluate the representativeness of internal runoff measurements in other sinkhole microbasins.
Soil-moisture sensors measured soil moisture continuously near the ET flux tower. Continuous measurements of water content at 2.5 cm, 5 cm, and 9 cm depths were made using Campbell Scientific water content reflectometer probes (CS615) installed horizontally. Soil temperature and heat flux were measured continuously at depths of 2.5 and 10 cm using thermocouple probes and heat flux plates. Heat flux plates were installed at a depth of 5 cm, and storage heat flux in the zero to 5 cm layer was calculated from both soil temperature measurements at 2.5 cm depth and estimates of heat [39] . Gravimetric soil moisture samples were collected at various sites and depths near the ET flux tower over various surface moisture conditions, as described by Black [40] , in order to calibrate the soil-moisture sensors. The water balance interval was selected so that volumetric soil moisture was the same at the start and end, so that there is no significant change in soil moisture storage.
ET was measured nearly continuously using eddy covariance instruments placed 15-m high and above the tree canopy on a Rohn tower. Eddy covariance is the most direct method of measuring water vapor flux [41] . Measurements of wind speed and acoustic temperature were made with a three-dimensional sonic anemometer (CSAT-3, Campbell Scientific), and measurements of water vapor concentration were made with a Li-Cor LI-7500 open path infra-red gas analyzer at ten-hertz intervals. The Li-Cor LI-7500 was factory calibrated October 13, 2003 and field calibrated October 29, 2004.
The vertical component of airspeed and variations in absolute humidity were measured from mean humidity:
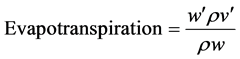 (2)
(2)
where:
w′ = vertical component of airspeed (time average in m/s);
ρv′ = variations in absolute humidity about the mean value (time average);
ρw = mean value of absolute humidity (converted from watts/m2 to mmoles/m2s to cm/30 min interval).
The readings represent average evapotranspiration for the fetch area, which varies with wind direction and sensor height. As a general guideline, the fetch ranges from 20 to 200 times the instrument height, with the farther fetch extending in the direction of prevailing winds [42] , although the actual fetch will vary with wind speed and other factors. The ET flux tower lies near the center of the Headquarters Flat sinkhole catchment, which has a 1-degree slope to the north, southeast, and southwest. The ground slope increases in elevation from the ET flux tower to the south at a maximum slope of 3 degrees. Because of the minimal slope in the direction of prevailing winds, the flux field was not rotated to account for slope.
Additional instruments used for meteorological and energy balance measurements include air temperature and humidity (HMP45C, Vaisala), net radiation (Radiation and Energy Balance Systems Q 7.1), incoming and upwelling solar radiation (LI-190 SB, Kipp and Zonen), and photosynthetic photon flux density (PPFD, LI-190SA, Li-Cor).
2.3. Data Analysis
The original 10-hertz datasets was pre-processed to calculate thirty-minute fluxes of latent heat and sensible heat for a 505-day test period following procedures outlined by Litvak et al. [43] . The ET data were filtered to remove poor-quality data, including readings taken when the wind approached the flux sensors from the north, where the tower distorts wind velocities, and during rain intervals. Initial data gaps were caused by power outages, lowering of the instrument for annual calibrations, and particulates (including raindrops) obscuring the glass lens of the gas analyzer. Of 24,285 thirty-minute intervals comprising the 505-day test period, 5585 data gaps were present after this quality filtering. The filtered ET values were corrected for Bowen ratio energy balance of sensible heat to latent heat, as described by Twine et al. [44] . To fill in the gaps remaining after filtering and energy balance, monthly correlations of post processed and filtered ET data were related to net radiation readings. On a monthly basis, the ET to net radiometer correlations had R2 correlations greater than 0.7 and averaged 0.83. Where gaps existed in the J17 tower net radiation record, readings from an ET flux tower located 21 km south on the Texas State University Freeman Ranch were used. Measured nighttime ET values are relatively very small so that data gaps of nighttime intervals are assumed to be zero. Following net radiation gap filling, 813 daytime 30-minute gaps remained, or 3% of the water-balance record. Where up to three consecutive 30-minute data gaps remained, the gaps were filled by averaging adjacent ET values. For 6 days, where larger data gaps remained, the daily total was calculated as 0.75 of the potential evapotranspiration values reported by Texas A & M University from a weather station at the City of Austin Davis Water Treatment Plant, based on an R2 correlation of 0.56. The accuracy of measuring an average evapotranspiration across the fetch area using eddy covariance with energy balance corrections is about ±5% [45] .
3. Results
The water balance for HQ Flat sink shows recharge and evapotranspiration percentages similar to karst areas across the world. Over a 505-day period, 68% of the rainfall returned to the atmosphere as evapotranspiration. The remaining 32% of the rainfall falling on the HQ Flat basin recharged with 26% infiltrating through the soils and percolating into the underlying bedrock (diffuse recharge) and about 6% flowing as discrete internal runoff recharging into the cave drain at the lowest point of the sinkhole (Figure 2). The 160 cm of rainfall measured over the 1.4 year reference interval was 42% above the local annual average rainfall of 81 cm. Volumetric soil moisture was 20% ± 2% at the start and end of the selected water balance interval, so no significant change in soil moisture storage occurred.

Figure 2. Water balance results for HQ Flat microbasin from April 2, 2004 to August 20, 2005 (505 days).
4. Discussion
The results from the 505-day water balance at HQ Flat Sink are strikingly similar to results a similar water balance study reported by Dugas et al. [34] where 65% of rainfall left as ET, 5% of precipitation became runoff, and 30% of precipitation recharged the Trinity Aquifer.
While measurements of ET were 68% of precipitation and discrete internal runoff into the cave entrance was 6% over an interval where precipitation was 42% higher than average, how much do these parameters, as well as diffuse recharge, vary at other sites and under climatic conditions? Over a single 2002 rain event, during which the ground was near saturation prior to precipitation, the amount of discrete internal runoff to HQ Flat Cave was 42% of the rainfall. Over a 1140-day interval under average precipitation conditions, discrete internal runoff to both HQ Flat Sink Cave and Flint Ridge Cave diminished to 3% of precipitation.
In order to examine variation in ET with precipitation conditions across Central Texas, ET/precipitation ratios reported from other climate towers were compiled and compared with annualized precipitation (Figure 3). These climate towers utilized either Bowen ratio or eddy covariance systems. Comparison of ET flux tower results indicate, as Dugas et al. [34] anticipated, that ET/precipitation ratios are inversely related to precipitation totals.
Distinct trends are indicated for above average and below average precipitation conditions. An equation that describes the relation between annual ET and precipitation during above average precipitation conditions is:
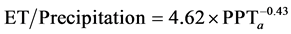 (3)
(3)
where PPTa = annualized precipitation in centimeters.
For below average precipitation, the relation between annual precipitation and ET may be steeper such as:
 (4)
(4)
While the towers are widely spaced both on the Edwards Aquifer and Trinity Aquifer, with variation in vegetation and soils, the trend has surprisingly limited variation. At average and above annual rainfall conditions, the data points for the ratio of ET/precipitation lie within 10% of the trend line. Under average Austin precipitation of 81 cm, an ET/precipitation ratio of 69% is indicated, although measured ET/precipitation ratio data points within 5 cm of 81 cm annual average precipitation actually range between 78% and 65%.
With 69% of rainfall lost to ET (ranging 65% to 78%) and 3% of rainfall allocated to runoff, the remaining 28% (ranging 19% to 32%) of precipitation would be expected to percolate into the underlying aquifer as autogenic recharge under average annual precipitation, based on the Equations (2) and (3) and actual data points under average conditions.
Aquifer recharge is focused during intervals of higher precipitation. In intervening areas between major creek channels, most autogenic recharge is expected to be focused for short periods around precipitation events. Shortterm ET measurements from the HQ Flat research station demonstrate that ET is minimal during the intervals where most autogenic recharge occurs (Figure 4). On an annual scale, most autogenic recharge occurs during
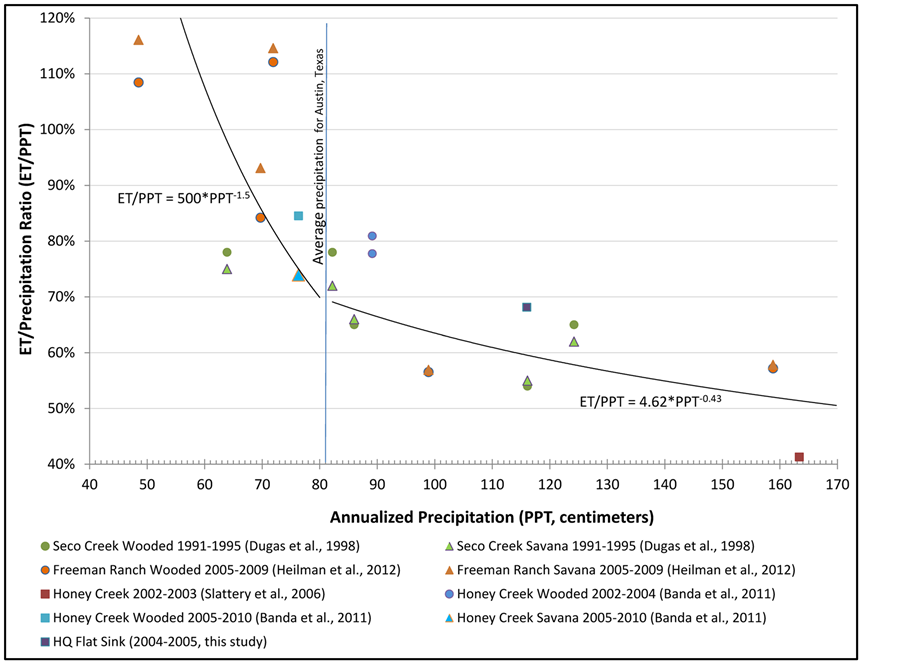
Figure 3. Central Texas ET flux tower data and annual precipitation.
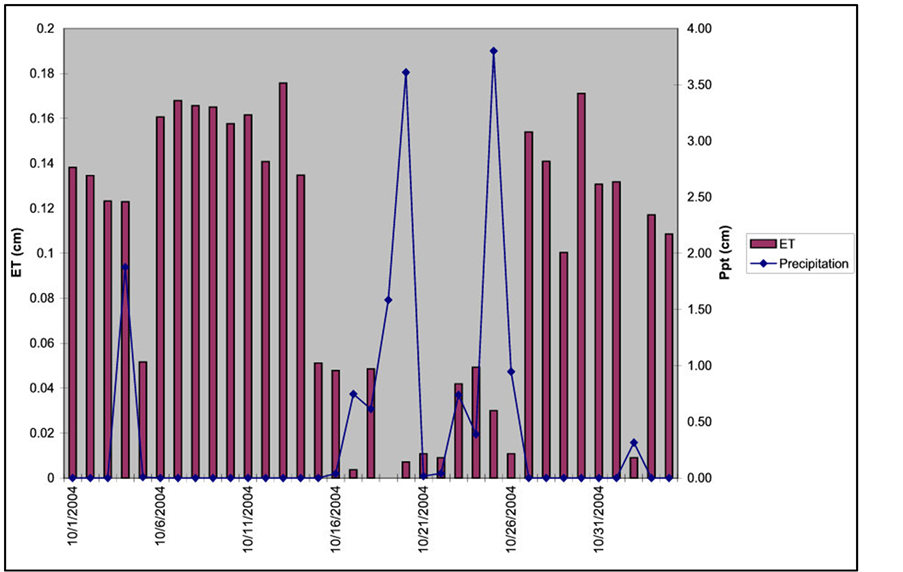
Figure 4. HQ Flat short-term response of ET to precipitation.
years of higher than average precipitation when measured ET/precipitation ratios ranged from 70% to 55%, allowing 30% to 45% of precipitation to be distributed as the combination of recharge and runoff. Over sufficiently large intervals, the climate tower approach to measuring recharge accurately accounts at a site scale for the later release of water from storage in soil and plants as ET.
5. Conclusions
As the largest component of precipitation water balance, measurement of ET using eddy covariance climate tower provides one of the most precise measurements of recharge, the next largest component of the water balance. Precipitation, ET, runoff, and soil moisture were monitored over a 505-day water balance interval, during which time precipitation was 42% higher than average and volumetric soil moisture was 20% ± 2% at the beginning and end. ET measured 68% of precipitation and internal runoff into the cave drain was 5%, and diffuse recharge was 26%. While internal runoff recharge and diffuse recharge totaled 32% over the water balance interval within the HQ Flat Sink research site, since internal drainage basins constitute only about 10% of the recharge area of the Barton Springs Segment, the diffuse recharge component of precipitation may be more representative overall of autogenic recharge over the Barton Springs Segment.
Based on compilation of ET data from other flux towers in Central Texas under a wide variety of annual precipitation conditions, it can be estimated that under average precipitation conditions, 69% of rainfall leaves as ET; 28% of rainfall percolates as autogenic recharge into the Edwards Aquifer. Based on a longer 1140-day measurement of internal runoff at HQ Flat and Flint Ridge under average rainfall conditions, the remaining 3% of rainfall is representative for runoff in intervening in the recharge area. During years which precipitation is greater than average, ET decreases to between 55% and 70% of precipitation as recharge and runoff proportionally increases to the remaining 30% to 45% of precipitation.
Acknowledgements
The expertise and experience of Dr. Marcy Litvak, currently of University of New Mexico, was critical for constructing and operating the flux tower, including flux sensor calibration and data analysis. William Asquith of the US Geological Survey assisted in establishing the flux tower. The University of Texas provided use of Li Cor LI-7500 flux sensors. The City of Austin Watershed Protection Department provided a majority of purchased supplies and labor, including concrete foundation, aluminum flumes, rain gauges, and ISCO 3230 flow meters. The Hill Country Conservancy provided $10,000 in supplies for the tower, including data logger and laptop. The University of Texas Lady Bird Johnson Wildflower Center provided a net radiometer used in the study. The City of Austin Water Quality Protection Land program provided the research site, assisted in site security, and provided supplies including the Rohn tower. City of Austin Electric Department provided use of a crane and crew to lift the tower. David Johns of the City of Austin Watershed Protection Department provided valuable review comments for this paper.
References
- White, D.E. (1965) Saline Waters in Sedimentary Rocks. In: Young, P. and Galley, J.E., Eds., Fluids in the Subsurface Environment, American Association of Petroleum Geologists Memoirs, 4, 342-365.
- Sukhija, B.S., Reddy, D.V., Nagabhushanam, P., Hussain, S., Giri, V.Y. and Patil, D.J. (1996) Environmental and Injected Tracers Methodology to Estimate Direct Precipitation Recharge to a Confined Aquifer. Journal of Hydrology, 177, 77-97. http://dx.doi.org/10.1016/0022-1694(95)02788-2
- Hendrickx, J.M. and Walker, G. (1997) Recharge from Precipitation, Chapter 2. In: Simmers, I., Ed., Recharge of Phreatic Aquifers in (Semi)-Arid Areas, IAH Contributions to Hydrogeology Series, Taylor and Francis, Balkema, Rotterdam.
- Scanlon, B.R. (2000) Uncertainties in Estimating Water Fluxes and Residence Times Using Environmental Tracers in an Arid Unsaturated Zone. Water Resources Research, 36, 395-409. http://dx.doi.org/10.1029/1999WR900240
- Moller, P., Weise, S., Tesmer, M., Dulski, P., Pekdeger, A., Bayer, U. and Magri, F. (2008) Salinization of Groundwater in the North German Basin: Results from Conjoint Investigation of Major, Trace Element and Multi-Isotope Distribution. International Journal of Earth Science, 97, 1057-1073. http://dx.doi.org/10.1007/s00531-007-0211-1
- White, W.B. (1977) Conceptual Models for Carbonate Aquifers: Revisited. In: Diliamarter, R.R. and Csallany, S.C., Eds., Hydrologic Problems in Karst Regions, Western Kentucky University, Bowling Green, 176-187.
- Zebidi, H. (1984) Chapter 4 Hydrology of Carbonate Areas, 4.3 Infiltration. In: La Moreaux, P., Wilson, B.M. and Memon, B.A., Eds., Guide to the Hydrology of Carbonate Rocks, Studies and Reports in Hydrology 41, UNESCO, Paris, 134.
- Lerner, D.N., Issar, A.S. and Simmers, I. (1990) Groundwater Recharge: A Guide to Understanding and Estimating Natural Recharge. IAH International Contributions to Hydrogeology, 8, Taylor and Francis, Balkema, Rotterdam.
- De Vries, J.J. and Simmers, I. (2002) Groundwater Recharge: An Overview of Processes and Challenges. Hydrogeology Journal, 10, 5-17. http://dx.doi.org/10.1007/s10040-001-0171-7
- Atkinson, T.C. (1977) Diffuse Flow and Conduit Flow in Limestone Terrain in the Mendip Hills, Somerset, UK. Journal of Hydrology, 35, 1-2, 93-110. http://dx.doi.org/10.1016/0022-1694(77)90079-8
- Dublyanskii, V.N., Pribluda, V.D. and Kodzhaspirov, A.A. (1984) Evaluation of the Karst-Water Balance of the Southwestern Upland Crimea. In: Castany, G., et al., Eds., Hydrogeology of Karstic Terrains, Case Histories, 1, 18-20.
- Mink, J.F. and Vacher, H.L. (1997) Hydrogeology of Northern Guam. In: Vacher, H.L. and Quinn, T., Eds., Geology and Hydrogeology of Carbonate Islands, Elsevier Science, Amsterdam, 743-761.
- Jocson, U., Jenson, J.W. and Contractor, D.N. (2002) Recharge and Aquifer Response: Northern Guam Lens Aquifer, Guam, Mariana Islands. Journal of Hydrology, 260, 231-254. http://dx.doi.org/10.1016/S0022-1694(01)00617-5
- Tixeront, J., Berkaloff, E., Caine, A. and Mauduech, E. (1951) Biland’eau des massifs calcaires en Tunisie Gaz des captages de Tumis et de Bizerte. IAHS, Assemblee de Bruxelles.
- Schoeller, H. (1948) Le regime hydrogeologique des calcaires, Eocene du synclinal du Dyr El Kef (Tunisie). Bulletin de la Societe Geologique de France, 5, 167-180.
- Zebidi, H. (1963) Contribution a l’etude du Bilan Hydrogeologique du Djebel Bargou. These Publication, B.I.P.H., Tunisie.
- Mero, F. (1958) Hydrological Investigations of the Na’aman Spring Region. Unpublished Water Planning for Israel Limited Report, Tel Aviv, Tahal.
- Goldschmidt, M.J. and Jacobs, M. (1958) Precipitation over and Replenishment of the Yarqon and Nahal Hatteninim Underground Catchments. Hydrological Service, Ministry of Food Agriculture, Israel.
- Mandel, S. and Shiftan, Z.L. (1981) Groundwater Resources: Investigation and Development. Academic Press, New York.
- Burdon, D.J. (1961) Groundwater Development and Conservation in Syria. FAO/ETAP Report 1270.
- Voute, C. (1961) A Comparison between Some Hydrological Observations Made in the Jurassic and Cenomian Limestone Mountains Situated to the West and to the East of the Ghab Graben. In: Eaux souterraines dans les zones arides: Colloque d’Ath è nes, Association international d’hydrologie scientii que, Gentbrugge, 160-166.
- Al-Charide, A. (2012) Recharge Rate Estimation in the Mountain Karst Aquifer System of Figeh Spring, Syria. Environmental Earth Sciences, 65, 1169-1178.
- Hoetzl, H. (1995) Groundwater Recharge in an Arid Karst Area (Saudi Arabia). International Association for Housing Science, 195-207.
- Aronis, G., Burdon, D.J. and Zeris, K. (1961) Development of a Karst Limestone Spring in Greece. Report from UNESCO, Ground Water Resources, Athens.
- Burdon, D.J. and Papakis, N. (1963) Handbook of Karst Hydrogeology with Special Reference to the Carbonate Aquifers of the Mediterranean Region: Athens, Greece. United Nations Special Fund Karst Groundwater Investigations, Institute for Geology and Subsurface Research, 276.
- Hauwert, N.M. (2009) Groundwater Flow and Recharge within the Barton Springs Segment of the Edwards Aquifer, Southern Travis County and Northern Hays County, Texas. PhD Dissertation, University of Texas at Austin, Austin, 328. http://repositories.lib.utexas.edu/handle/2152/14107
- Hill, R.T. (1892) On the Occurrence of Artesian and Other Underground Waters in Texas, New Mexico, and Indian Territory: Together with the Geology and Geography of Those Regions. US Geological Survey Report, 166.
- De Cook, K.J. (1957) Geology of San Marcos Quadrangle, Hays County, Texas. MA Thesis, University of Texas at Austin, Austin, 90.
- Garza, S. (1962) Recharge, Discharge, and Changes in Ground-Water Storage in the Edwards and Associated Limestones, San Antonio Area, Texas—A Progress Report on Studies, 1955-59. Texas Board of Water Engineers Bulletin 6201.
- Slade, R., Dorsey, M. and Stewart, S. (1986) Hydrology and Water Quality of the Edwards Aquifer Associated with Barton Springs in the Austin Area, Texas. US Geological Survey Water-Resources Investigations Report 86-4036, Austin.
- Woodruff, C.M. (1984) Water Budget Analysis for the Area Contributing Recharge to the Edwards Aquifer, Barton Springs Segment. In: Woodruff, C. and Slade, R., Eds., Hydrogeology of the Edwards Aquifer-Barton Springs Segment, Travis and Hays Counties, Texas, Austin Geological Society Guidebook 6, 36-42.
- Harrison, A. (1996) Recharge Mechanisms of Swelling Clays and Shales, Central Texas. MS Thesis, Baylor University, Waco.
- Slade, R. (2014) Documentation of a Recharge-Discharge Water Budget and Main Streambed Recharge Volumes, and Fundamental Evaluation of Groundwater Tracer Studies for the Barton Springs Segment of the Edwards Aquifer. Texas Water Resources Institute, Austin. Texas Water Resources Journal, 5, 12-23.
- Dugas, W.A., Hicks, R.A. and Wright, P. (1998) Effect of Removal of Juniperus ashei on Evapotranspiration and Runoff in the Seco Creek Watershed. Water Resources Research, 34, 1499-1506. http://dx.doi.org/10.1029/98WR00556
- Huang, Y. and Wilcox, B.P. (2005) How Karst Features Affect Recharge—Implications for Estimating Recharge to the Edwards Aquifer.10th Multidisciplinary Conference on Sinkholes and the Engineering and Environmental Impact of Karst, Geotechnical Special Publication No. 144, 201-206.
- Slattery, R.N., Furlow, A.L. and Ockerman, D.J. (2006) Hydrologic and Water-Quality Data, Honey Creek State Natural Area, Comal County, Texas, August 2001-September 2003. US Geological Survey Data Series 200.
- Banta, J.R. and Slattery, R.N. (2011) Effects of Brush Management on the Hydrologic Budget and Water Quality in and Adjacent to Honey Creek State Natural Area, Comal County, Texas, 2001-10. US Geological Survey SRI Report 2011-5226, Reston, 34.
- Heilman, J.L., Litvak, M.E., McInnes, K.J., Kjelgaard, J.F., Kamps, R.H. and Schwinning, S. (2012) Water-Storage Capacity Controls Energy Partitioning and Water Use in Karst Ecosystems on the Edwards Plateau, Texas. Ecohydrology, 7, 127-138.
- Kimball, B.A. and Jackson, R.D. (1979) Modification of the Aerial Environment of Crops: Soil Heat Flux. ASAE Monograph 2, American Society of Agricultural Engineers, 211-229.
- Black, C.A. (1965) Methods of Soil Analysis: Part I Physical and Mineralogical Properties. American Society of Agronomy, Madison.
- Burba, G. (2013) Eddy Covariance Method for Scientific, Industrial, Agricultural and Regulatory Applications: A Field Book on Measuring Ecosystem Gas Exchange and Areal Emission Rates. Li-Cor Biosciences, Lincoln.
- Monteith, J.L. and Unsworth, M.H. (1990) Principles of Environmental Physics. 2nd Edition, Butterworth-Heinemann, Elsevier, Oxford.
- Litvak, M.E., Miller, S., Wofsy, S.C. and Goulden, M. (2003) Effect of Stand Age on Whole Ecosystem CO2 Exchange in the Canadian Boreal Forest. Journal of Geophysical Research, 108. http://dx.doi.org/10.1029/2001JD000854
- Twine, T.E., Kustas, W.P., Norman, J.M., Cook, D.R., Houser, P.R., Meyers, T.P., Prueger, J.H., Starks, P.J. and Wesely, M.L. (2000) Correcting Eddy-Covariance Flux Underestimates over a Grassland. Agricultural and Forest Meteorology, 103, 279-300. http://dx.doi.org/10.1016/S0168-1923(00)00123-4
- Ham, J.M. and Heilman, J.L. (2003) Experimental Test of Density and Energy Balance Corrections on Carbon Dioxide Flux as Measured Using Open-Path Eddy Covariance. Agronomy Journal, 95, 1393-1403. http://dx.doi.org/10.2134/agronj2003.1393

