Journal of Water Resource and Protection
Vol.6 No.5(2014), Article ID:45304,10 pages DOI:10.4236/jwarp.2014.65046
Mass Transfer in a Centrifugal Turbine Agitator-Pump
Valery Katz*, Gedalya Mazor
SCE—Sami Shamoon College of Engineering, Beer-Sheva, Israel
Email: *elidad@012.net.il
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 22 December 2013; revised 23 January 2014; accepted 22 February 2014
ABSTRACT
This article is a continuation of the research, centering on a vacuum-filtration system, which is designed to reduce the concentration of calcium in water; a process is also known as—water softening. The problem of solving the concentration distribution of the initial (embryonic) particles of CaCO3-particles, which were introduced into the limited volume of the apparatus with a turbine agitator-pump, is addressed through the use of diffusion and deterministic-stochastic models of mass transfer. The solution of the extreme problem allows determining the most important process parameters, such as time of dispersions homogenization and the dispersion mass flow rate to the surface of a special filter. For these parameters a comparative analysis of the adequacy of the theory was found through experiments, performed in the study. We found that uniform distribution of concentrations along the height of the apparatus is achieved by the angular velocity of the rotation 400 rpm for the turbine with 6 - 7 blades at the time of homogenization 14s. In this case, the dispersion mass flow to the surface of the cylindrical filter is ( 50 mg/s at an average concentration of the introduced CaCO3 particles, which is equal to 10 g/L. We determined that the accuracy of the results depends on: the coordinates of the material input in the apparatus volume, the surface shape of the filter and the volumetric flow rate of the liquid (water), being discarded by the turbine blades in the normal direction to their surface.
Keywords:Calcium Removal, Dispersion, Mass Transfer, Modeling, Adequacy

1. Introduction
A vacuum-filtration system, designed to reduce the concentration of calcium in the water during the water softening process was developed at the Applied Research Institute of Ben-Gurion University of the Negev (Israel) (Figure 1) [1] . The most important part of this system is centrifugal turbine agitator-pump, sucking and discarding flows of liquid (water) with suspended particles of CaCO3 (dispersed flow, dispersion, suspension) to the surface of a special filter. Hydrodynamics and mass transfer in such a turbine agitator-pump were studied and presented in [2] [3] . We calculated the main hydrodynamic parameters, which characterize the dynamic interaction of turbine blades with the flows of a viscous liquid. Based on the empirical Equation: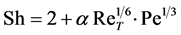 , the coefficients of mass transfer
, the coefficients of mass transfer  and diffusion (dispersion) coefficients
and diffusion (dispersion) coefficients  of the CaCO3 substance by mass transfer from liquid (water) to the surface of the initial (embryonic) spherical particles CaCO3, introduced in the apparatus with turbine agitator-pump, were calculated.
of the CaCO3 substance by mass transfer from liquid (water) to the surface of the initial (embryonic) spherical particles CaCO3, introduced in the apparatus with turbine agitator-pump, were calculated.
The purpose of this paper is:
 To present a solution to problem of distribution of CaCO3 particles in a limited volume of the apparatus with a turbine agitator-pump;
To present a solution to problem of distribution of CaCO3 particles in a limited volume of the apparatus with a turbine agitator-pump;
 To determine the most important technological process parameters, such as time of dispersion homogenization
To determine the most important technological process parameters, such as time of dispersion homogenization 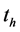 and the dispersion mass flow rate to the filter surface
and the dispersion mass flow rate to the filter surface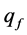 ;
;
 To use experimentation to conduct an analysis of the adequacy of the theory.
To use experimentation to conduct an analysis of the adequacy of the theory.
2. Models of Mass Transfer
2.1. Diffusion Model
To determine the function of the concentration distribution  for dispersed particles of CaCO3 in a limited volume of the apparatus with a turbine agitator-pump, in the absence of mass exchange, we use the following three-dimensional Equation:
for dispersed particles of CaCO3 in a limited volume of the apparatus with a turbine agitator-pump, in the absence of mass exchange, we use the following three-dimensional Equation:
 (1)
(1)
with initial and boundary conditions in the following form:
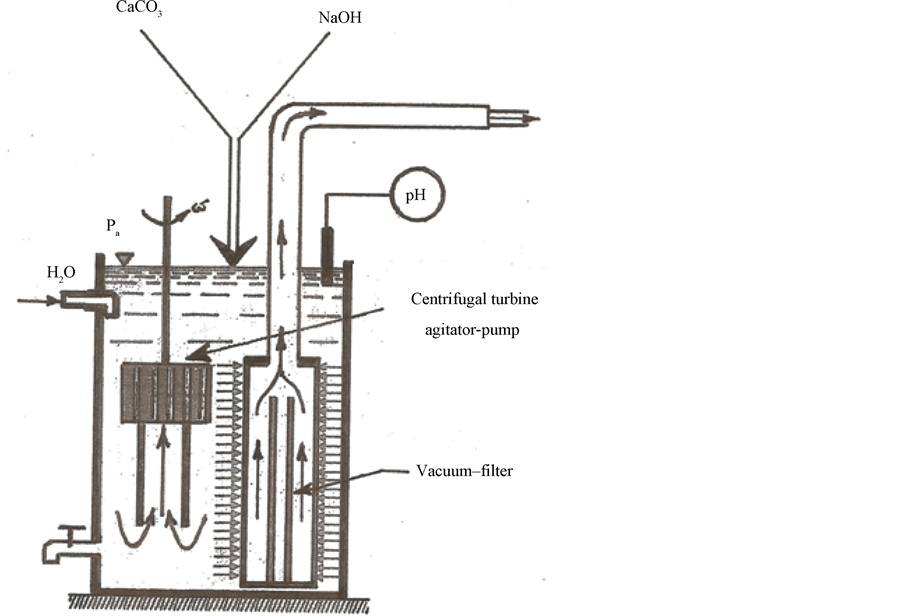
Figure 1. Vacuum-filtration system.

where ![]() represents the relative velocity of the particle;
represents the relative velocity of the particle; , which is the diffusion (dispersion) coefficients;
, which is the diffusion (dispersion) coefficients;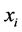 , which are cylindrical coordinates (
, which are cylindrical coordinates (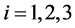 and match
and match ). The
). The 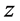 axis is directed vertically upward from the center of the apparatus bottom.
axis is directed vertically upward from the center of the apparatus bottom. 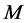 is the mass of all CaCO3 particles, introduced into the apparatus volume
is the mass of all CaCO3 particles, introduced into the apparatus volume 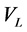 at point
at point ![]() in order to be distributed.
in order to be distributed. —represents specific dispersion fluxes to the bounding surface
—represents specific dispersion fluxes to the bounding surface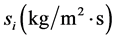 ;
;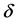 —being the Dirac delta function [4] . The function
—being the Dirac delta function [4] . The function 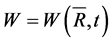 in (1) is the probability of finding the particles group, moved and do not interacting with each other at time
in (1) is the probability of finding the particles group, moved and do not interacting with each other at time 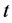 at point
at point ![]() where
where 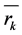 represents the movements of individual particles.
represents the movements of individual particles. 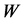 serves as a diffusing component (particles) concentration
serves as a diffusing component (particles) concentration 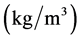 at point
at point 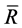 in the time
in the time .
.
The conclusion and solution of the equation (1) in the case of wandering particles with constant speeds 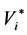 and coefficient
and coefficient 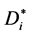 in the infinite volume are given, for example, by Chandrasekhar [5] . A similar approach to the description of the diffusion in the liquid suspended particles was used by Landau and Lifshitz [6] . Thus, the solution of the Equation (1) with the above mentioned initial conditions is represented in form [7] :
in the infinite volume are given, for example, by Chandrasekhar [5] . A similar approach to the description of the diffusion in the liquid suspended particles was used by Landau and Lifshitz [6] . Thus, the solution of the Equation (1) with the above mentioned initial conditions is represented in form [7] :
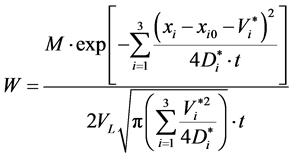 (2)
(2)
The dimension of the distribution function of the concentration 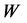 is
is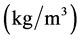 . The parameter
. The parameter 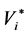 and
and 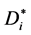 averaged velocities
averaged velocities 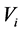 and diffusion coefficients
and diffusion coefficients 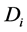 in the relative (to the liquid) motion of the particles. They are determined as:
in the relative (to the liquid) motion of the particles. They are determined as:
 (3)
(3)
Here  is the number of displacements of particles per unit of time;
is the number of displacements of particles per unit of time; —respectively, the average displacements and mean square displacements of the diffusing particles. It is known, that they represent the first and second initial moments of the regulatory function
—respectively, the average displacements and mean square displacements of the diffusing particles. It is known, that they represent the first and second initial moments of the regulatory function 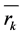 for displacement of individual particles.
for displacement of individual particles.
2.2. Deterministic-Stochastic Model
The problem of determining such a function is reduced to the solution of the stochastic differential Langevin Equation [8] for the motion of dispersed particles in an external force field:
 (4)
(4)
This is derived from the most general Meshcherskij Equation [9] . Here ![]() are active forces, acting on the particles;
are active forces, acting on the particles;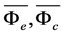 , which are the inertial forces in the portable motion of particles with the liquid and Coriolis force of inertia, respectively;
, which are the inertial forces in the portable motion of particles with the liquid and Coriolis force of inertia, respectively;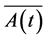 —is the perturbing acceleration, which is characteristic of the random effects on the particle by the surrounding liquid. The function
—is the perturbing acceleration, which is characteristic of the random effects on the particle by the surrounding liquid. The function  has the following statistical properties: it does not depend on the relative velocity
has the following statistical properties: it does not depend on the relative velocity 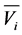 and it changes quite rapidly, when compared with the
and it changes quite rapidly, when compared with the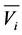 .
.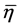 —change correction vector, which theoretically depends on the geometry of the apparatus with the turbine, the kinematical and the physical parameters of the process.
—change correction vector, which theoretically depends on the geometry of the apparatus with the turbine, the kinematical and the physical parameters of the process.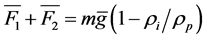 —represents particle weight and the lifting Archimedes force;
—represents particle weight and the lifting Archimedes force;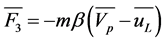 —describes resistance force, involved in the relative motion of the particles.
—describes resistance force, involved in the relative motion of the particles.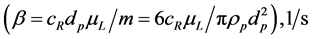 ;
;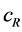 —being the resistance coefficient, which depends on the concentration of the dispersed phase (particles of CaCO3) and the mass transfer from the liquid to the surface of the particles (for the Stokes resistance force
—being the resistance coefficient, which depends on the concentration of the dispersed phase (particles of CaCO3) and the mass transfer from the liquid to the surface of the particles (for the Stokes resistance force ).
). 
where![]() —represents the centripetal acceleration and rotation acceleration of the carrier medium respectively;
—represents the centripetal acceleration and rotation acceleration of the carrier medium respectively; ![]() by
by 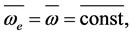
![]() ,
,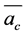 —Coriolis acceleration;
—Coriolis acceleration;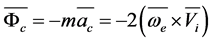 . Equation (4) models the Brownian motion of dispersed particles in the presence of external force fields as a Markov process in phase velocity space
. Equation (4) models the Brownian motion of dispersed particles in the presence of external force fields as a Markov process in phase velocity space . We write further the Equation (4) in the projection on the axis of the moving coordinate system
. We write further the Equation (4) in the projection on the axis of the moving coordinate system  showing it to be rigidly attached to a rotating turbine and neglecting the Coriolis force, as shown below:
showing it to be rigidly attached to a rotating turbine and neglecting the Coriolis force, as shown below:
 (5)
(5)
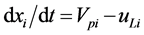 the relative velocity of the particle, projected on the axis
the relative velocity of the particle, projected on the axis 
 .
.
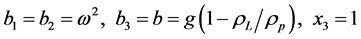 .
.
The first two Equations in (5) are identical in appearance. From these equations we must find the probability distributions  and
and 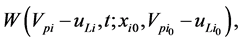 which respectively mean the probability of finding the relative displacement
which respectively mean the probability of finding the relative displacement 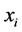 and the relative velocity
and the relative velocity  of the particle at a time
of the particle at a time , if initially at
, if initially at 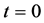 the particle was in position
the particle was in position 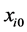 and had an initial speed
and had an initial speed . To get this distribution we must first find a formal solution of the Equation (5). This can be done, for example, by the method of variation of parameters [5] , considering Equation (5) as an ordinary differential equation. We can then bring the solution to the following form:
. To get this distribution we must first find a formal solution of the Equation (5). This can be done, for example, by the method of variation of parameters [5] , considering Equation (5) as an ordinary differential equation. We can then bring the solution to the following form: , where
, where 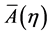 has the same properties as
has the same properties as 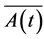 in (4)
in (4)
and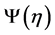 —is the function, that is specified by a decision (5). Then, according to (5), the probability distribution of the vector
—is the function, that is specified by a decision (5). Then, according to (5), the probability distribution of the vector 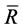 is given by:
is given by:
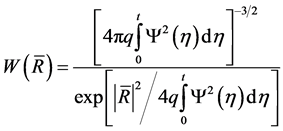 (6)
(6)
where 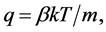
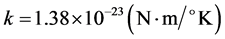 —is the Boltzmann constant [8] . Using the above findings and omitting the intermediate calculations, we write the expression for the displacement of the individual particles
—is the Boltzmann constant [8] . Using the above findings and omitting the intermediate calculations, we write the expression for the displacement of the individual particles 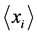 and their relative velocities
and their relative velocities  in the form [7] :
in the form [7] :
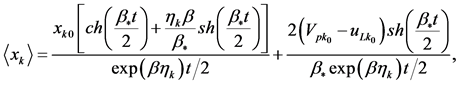 (7)
(7)
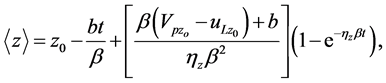
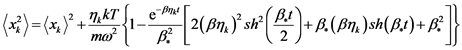
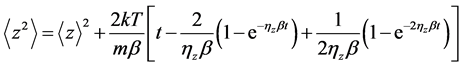
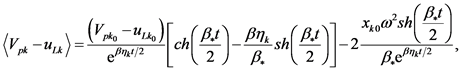
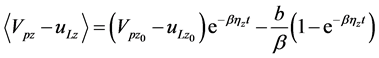 .
.
There  and corresponds to the direction of the axes
and corresponds to the direction of the axes 
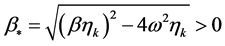 ;
;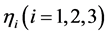 —are correction vector projections on axes of cylindrical coordinate system
—are correction vector projections on axes of cylindrical coordinate system 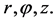
2.3. Calculation of Diffusion Coefficients. Relative Velocities of Particles We first determine the number of positive displacements of particles per unit of time 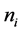 along the axes
along the axes 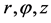
as follows: . Using Equations (3) and (7), for the diffusion (dispersion) coefficient
. Using Equations (3) and (7), for the diffusion (dispersion) coefficient 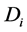 we have:
we have:
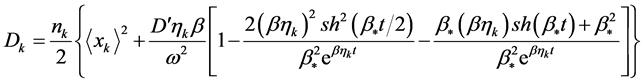 (8)
(8)
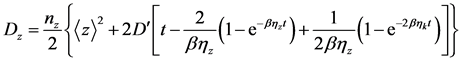
 —is the coefficient of Brownian diffusion, having, for example, the value:
—is the coefficient of Brownian diffusion, having, for example, the value: 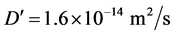 for parameters of [3] :
for parameters of [3] :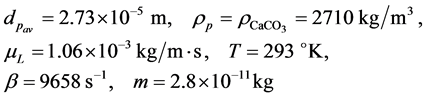 .
.
Due to the smallness of the , second summands in (8) can be neglected. Then the formulas
, second summands in (8) can be neglected. Then the formulas 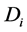 will take the form of:
will take the form of:
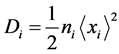 (9)
(9)
The combination of Equation (9) with Equation (7) shows, that, if the initial velocities  of the particles coincide with the carrier medium velocities
of the particles coincide with the carrier medium velocities 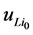 (in the case
(in the case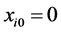 ,
,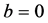 ) the diffusion coefficient
) the diffusion coefficient  This is consistent with the physical meaning of the process. Formula (9) are valid for the values of the coefficients
This is consistent with the physical meaning of the process. Formula (9) are valid for the values of the coefficients 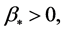 that is, when
that is, when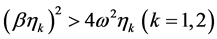 . If
. If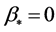 , then
, then 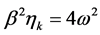 and for the diameter of the diffusing particles CaCO3 we have the relations:
and for the diameter of the diffusing particles CaCO3 we have the relations:
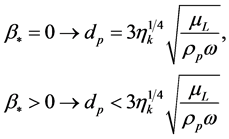 (10)
(10)
Therefore for a water softening process the value of the particle diameter  and the correction factor
and the correction factor 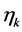 can be estimated. For the data from [3] we have:
can be estimated. For the data from [3] we have: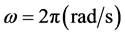
 ; hence, the approximate value of the coefficient
; hence, the approximate value of the coefficient  at
at 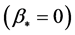 is:
is: . Because the distribution function
. Because the distribution function 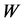 of Equation (2) consists of the relative velocity with the diffusion coefficients having constant value, the expression obtained for
of Equation (2) consists of the relative velocity with the diffusion coefficients having constant value, the expression obtained for  from Equation (7) and for
from Equation (7) and for 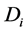 from Equation (9) should be averaged over time. We take as an averaging time interval the time of dispersion homogenization
from Equation (9) should be averaged over time. We take as an averaging time interval the time of dispersion homogenization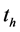 , that is, the time to reach an average concentration
, that is, the time to reach an average concentration 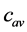 of the diffusing component throughout the apparatus volume, while:
of the diffusing component throughout the apparatus volume, while:
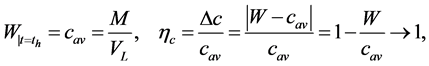
where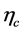 —is the coefficient of heterogeneity of the concentration of the component in the volume of the apparatus. We have:
—is the coefficient of heterogeneity of the concentration of the component in the volume of the apparatus. We have:
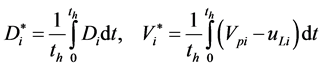 (11)
(11)
Replace the exponential terms in Equations (7) and (9) at their approximate values [9] :
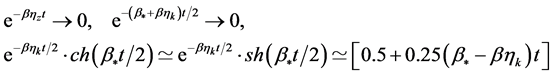
Then at the point of mass 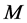 input
input 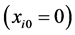 for average
for average  from Equation (11) we obtain:
from Equation (11) we obtain:
 (12)
(12)
A further task is to determine the time of dispersion homogenization .
.
3. Process Parameters and Adequacy
3.1. Time Homogenization of Dispersion
Consider the following extreme problem: .
.
Substituting the function  from Equation (2), for the dispersion homogenization time
from Equation (2), for the dispersion homogenization time 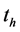 we obtain the following expression:
we obtain the following expression:
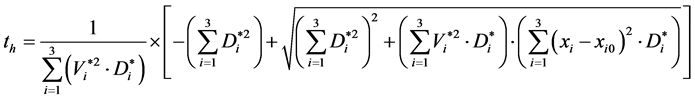 (13)
(13)
The diffusion coefficient 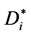 and the relative velocities
and the relative velocities 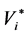 in Equation (13) also contain unknown parameter
in Equation (13) also contain unknown parameter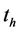 . Therefore, the calculation of
. Therefore, the calculation of 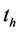 is required in order to carry out an iterative method. As a first approximation we can use parameter values from [3] and the dimensionless Equation for the time of homogenization
is required in order to carry out an iterative method. As a first approximation we can use parameter values from [3] and the dimensionless Equation for the time of homogenization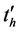 , obtained by study of the suspensions homogenization process in apparatuses with stirrers [7] , as follows:
, obtained by study of the suspensions homogenization process in apparatuses with stirrers [7] , as follows:
 (14)
(14)
Here 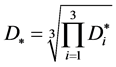 is the average value of the diffusion (dispersion) coefficient;
is the average value of the diffusion (dispersion) coefficient; 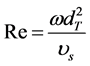 is the Rey nolds number for turbine;
is the Rey nolds number for turbine; ,
,
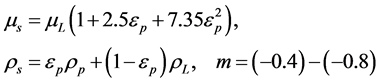 Due to component CaCO3 concentration
Due to component CaCO3 concentration 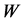 at the time of homogenization
at the time of homogenization 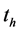 tends to its average value
tends to its average value 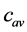 throughout the apparatus volume and does not depend on the coordinates shown in (Figure 2). The exponential term in Equation (2) can be neglected and for controlled precision of calculation
throughout the apparatus volume and does not depend on the coordinates shown in (Figure 2). The exponential term in Equation (2) can be neglected and for controlled precision of calculation 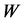 we can use the following simple formula:
we can use the following simple formula:
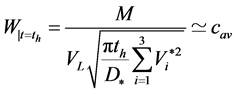 (15)
(15)
Table 1, we present the values of homogenization time 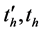 and the average concentration
and the average concentration 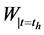 which
which

Figure 2. Distribution of  concentration.
concentration.
Table 1. Time of homogenization and average concentration.
are calculated by the empirical data of [2] [3] , Equations (14) and (15) and the analytical formulas shown in Equations (12) and (13).
As seen from Table 1, using the formulas in Equations (13) and (14) for calculating the homogenization time , gives almost perfectly matched results for the above presented values of the geometrical and phy-sical parameters. An important role is played by the coordinates
, gives almost perfectly matched results for the above presented values of the geometrical and phy-sical parameters. An important role is played by the coordinates  of the substance input point in the volume of the apparatus. Calculation results for average concentration
of the substance input point in the volume of the apparatus. Calculation results for average concentration , according to formula in Equation (15), are consistent with the experimental data, presented in Figure 2, for turbine agitator-pumps numbered 1
, according to formula in Equation (15), are consistent with the experimental data, presented in Figure 2, for turbine agitator-pumps numbered 1 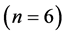 and 2
and 2  at angular velocities of rotation
at angular velocities of rotation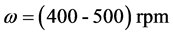 . Deviation values
. Deviation values 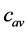 of about
of about  correspond to a turbine agitator-pump number
correspond to a turbine agitator-pump number 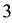 with the number of blades shown as
with the number of blades shown as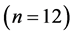 .
.
3.2. Mass Flows of Dispersion
We describe in Equation (16) the dynamic boundary conditions for the dispersed flow of particles, flowing through the turbine agitator-pump, with the achievement of the homogenization time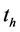 :
:
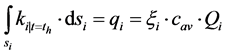 (16)
(16)
Here 
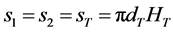 —is the lateral surface of the turbine;
—is the lateral surface of the turbine;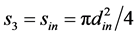 —is the cross-section area of the turbine suction tube;
—is the cross-section area of the turbine suction tube;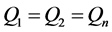
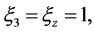 —is the volumetric flow of liquid (water) discharged by the turbine blades in the normal direction to their surface,
—is the volumetric flow of liquid (water) discharged by the turbine blades in the normal direction to their surface,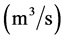 ;
;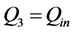 —is the flow rate at the inlet to the turbine suction pipe; and
—is the flow rate at the inlet to the turbine suction pipe; and —represents proportionality factors. Expressions in the Equation (16) are dispersion mass flows in
—represents proportionality factors. Expressions in the Equation (16) are dispersion mass flows in  in the inlet
in the inlet  and outlet
and outlet 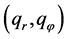 of the turbine agitator-pump. At the same time should be valid the law of mass conservation, then:
of the turbine agitator-pump. At the same time should be valid the law of mass conservation, then: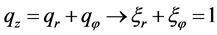 .
.
Using the results of the experiments, presented in [2] [3] , we can determine the mass flow rate of the dispersion to the filter surface 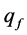 with use of the formula, shown in the Equation (17):
with use of the formula, shown in the Equation (17):
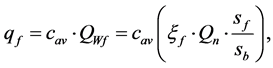 (17)
(17)
where![]() —is the volumetric flow rate of water, cleaned from CaCO3—particles, passing through the filter surface and
—is the volumetric flow rate of water, cleaned from CaCO3—particles, passing through the filter surface and  represents the proportionality factor for the filter;
represents the proportionality factor for the filter; —represents lateral surface of the filter;
—represents lateral surface of the filter;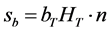 —represents the surface of
—represents the surface of 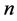 turbine blades and
turbine blades and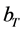 —represents the distance between the centers of macro vortices, formed in the rear region after screws [3] . Table 2, below, is an example of calculating the mass flows of dispersion
—represents the distance between the centers of macro vortices, formed in the rear region after screws [3] . Table 2, below, is an example of calculating the mass flows of dispersion 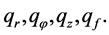
Table 2. Mass flows of dispersion: example of calculation.
From Table 2 and Equation (17) we see, that in order to increase the mass flow rate of dispersion to the surface of the filter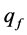 , we must first increase its surface
, we must first increase its surface 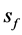 and increase the normal flow rate of liquid
and increase the normal flow rate of liquid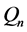 . The boundary conditions, expressed through Equation (16), can be used for analytical determination of the correction
. The boundary conditions, expressed through Equation (16), can be used for analytical determination of the correction . For that to take effect, we need to substitute into Equation (16) the distribution function of the concentration
. For that to take effect, we need to substitute into Equation (16) the distribution function of the concentration  from Equation (2) and the relative velocity
from Equation (2) and the relative velocity 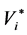 and the diffusion coefficient
and the diffusion coefficient 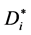 from Equation (12). However, the expressions for
from Equation (12). However, the expressions for 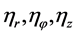 are too cumbersome. Therefore, the calculation of
are too cumbersome. Therefore, the calculation of 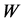 should be guided by the values of the coefficients in Table 1.
should be guided by the values of the coefficients in Table 1.
4. Conclusions The result of this research shows that the diffusion and deterministic-stochastic models of the substance transfer (particles of CaCO3) in a limited volume of apparatus with the turbine agitator-pump can be used as an attachment to the issue of the removal of calcium from water, a process often called water softening. The main results of the use of the developed mathematical and physical models are:
 Optimal distribution of CaCO3 particles concentrations within the volume of the apparatus is achieved by the angular velocity of rotation
Optimal distribution of CaCO3 particles concentrations within the volume of the apparatus is achieved by the angular velocity of rotation 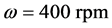 for the turbine with 6 - 7 blades and homogenization time of
for the turbine with 6 - 7 blades and homogenization time of  At that dispersion, mass flows to the surface of the cylindrical filter are
At that dispersion, mass flows to the surface of the cylindrical filter are 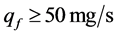 at an average concentration of
at an average concentration of ![]()
 The accuracy of the calculation process parameters for homogenization time
The accuracy of the calculation process parameters for homogenization time  and mass flow rate
and mass flow rate 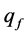 affects the coordinates of the input point
affects the coordinates of the input point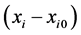 , the shape and surface of the filter
, the shape and surface of the filter 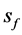 and the volumetric flow of liquid (water)
and the volumetric flow of liquid (water) 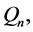 as discarded by turbine blades in the normal direction to their surface. Some hydrodynamic parameters involved in the calculation, such as the speed of the carrier medium (water)
as discarded by turbine blades in the normal direction to their surface. Some hydrodynamic parameters involved in the calculation, such as the speed of the carrier medium (water) , volumetric flow rates
, volumetric flow rates 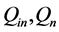 were calculated on the basis of the vortex hydrodynamic model, described in [2] . Mass transfer parameters, described as the average diffusion (dispersion) coefficients
were calculated on the basis of the vortex hydrodynamic model, described in [2] . Mass transfer parameters, described as the average diffusion (dispersion) coefficients 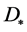 and the average diameters of the diffusing particles
and the average diameters of the diffusing particles , used in the calculations are taken from [3] , preceding to this study.
, used in the calculations are taken from [3] , preceding to this study.
 Some formulas, such as Equations (13)-(15), can be used in calculations of homogenization time for suspensions. They can also be used to determine average concentrations of diffusing components in various types of mixing devices and dispersion homogenizers.
Some formulas, such as Equations (13)-(15), can be used in calculations of homogenization time for suspensions. They can also be used to determine average concentrations of diffusing components in various types of mixing devices and dispersion homogenizers.
Acknowledgments
The authors are grateful to Professor J. Oren and Engineer N. Daltorphe (Ben-Gurion University of the Negev, Beer-Sheva, Israel) for help in carrying out experimental studies in a laboratory installation, designed for water softening (Figure 1).
Notations
 —accelerating the carrier medium (water),
—accelerating the carrier medium (water),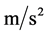 ;
;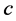 —concentration,
—concentration,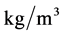 ;
;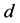 —the diameter of the particle, the turbine,
—the diameter of the particle, the turbine,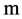 ;
;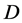 —the diffusion (dispersion) coefficient,
—the diffusion (dispersion) coefficient,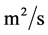 ;
; —the force,
—the force, ;
;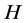 —the height,
—the height,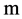 ;
;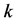 —the specific flow of the dispersion,
—the specific flow of the dispersion,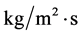 ; the mass transfer coefficient,
; the mass transfer coefficient,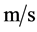 ;
;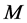 —mass,
—mass,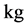 ;
;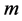 —mass,
—mass,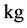 ; index;
; index; —the number of turbine blades;
—the number of turbine blades;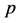 —pressure,
—pressure,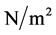 ;
;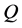 —volumetric flow rate of liquid (water),
—volumetric flow rate of liquid (water),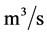 ;
;  -mass flow rate,
-mass flow rate,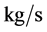 ;
;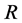 —radius,
—radius,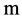 ;
;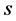 —surface,
—surface,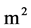 ;
;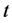 —time,
—time,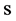 ;
; — temperature,
— temperature, ;
; —speed of the carrier medium (water),
—speed of the carrier medium (water),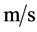 ;
; —the particle velocity,
—the particle velocity, ; the volume of the apparatus,
; the volume of the apparatus,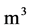 ;
;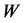 —the concentration of particles CaCO3,
—the concentration of particles CaCO3,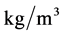 ;
;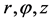 —coordinates,
—coordinates,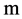 .
.
Greek symbols: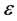 —the concentration of the initial (embryonic) particles of CaCO3, introduced into the volume of the apparatus,
—the concentration of the initial (embryonic) particles of CaCO3, introduced into the volume of the apparatus, ;
; —the dynamic viscosity coefficient,
—the dynamic viscosity coefficient,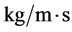 ;
;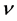 —the coefficient of kinematical viscosity,
—the coefficient of kinematical viscosity,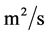 ;
; —density,
—density,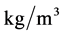 ;
;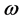 —angular velocity of the turbine,
—angular velocity of the turbine,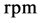 .
.
Indices: —apparatus;
—apparatus; —the average value;
—the average value; —the entrance to a suction tube of the turbine agitatorpump;
—the entrance to a suction tube of the turbine agitatorpump; —lateral surface;
—lateral surface; —Coriolis force of inertia;
—Coriolis force of inertia; —portable motion together with the turbine;
—portable motion together with the turbine; — filter;
— filter; —homogenization;
—homogenization; —liquid (water);
—liquid (water); —normal direction;
—normal direction; —particle of CaCO3
—particle of CaCO3 —resistance;
—resistance; —surface;
—surface; —turbine;
—turbine; —water;
—water; —radial, tangential and axial directions; 0—the initial value; *— the averaged value.
—radial, tangential and axial directions; 0—the initial value; *— the averaged value.
Criteria
 —Reynolds number;
—Reynolds number;
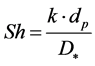 —Sherwood number;
—Sherwood number;
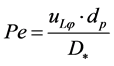 —Peclet number.
—Peclet number.
References
- Oren, V.K. and Daltorphe, N. (2001) Improved Compact Accelerated Precipitation Softening. A Pretreatment for Membrane Processes. Ben-Gurion University of the Negev, Institute for Applied Research, Beer-Sheva, Israel.
- Katz, V.Y. and Mazor, G. (2011) Hydrodynamics of a Centrifugal Turbine Agitator-Pump. Russian Journal of Applied Chemistry, Modeling and Calculation of Technological Processes, 84, 1655-1669. http://dx.doi.org/10.1134/S1070427211090345
- Katz, V.Y. and Mazor, G. (2013) Hydrodynamics and Mass Transfer in a Turbine Pump-Mixer. Proceedings of XXVI International Scientific Conference on Mathemati-cal Methods in Technique and Technologies-MMTT-26, May 27-30, 2013, N. Novgorod State Technical University named after Alekseev, N. Novgorod, Russia.
- Tikhonov, V.I. and Mironov, M.A. (1977) Markov Processes. Soviet Radio.
- Chandrasekhar, S. (1947) Stochastic Problems in Physics and Astronomy. Moscow.
- Landau, L.D. and Lifshitz, E.M. (1988) Theoretical Physics: A Training Manual, Vol. 6, Hydrodynamics. 4th Edition, Science, Moscow.
- Katz, V.Y. (1990) Doctoral Sci. (Tech.) Dissertation. KKhTI, Kazan.
- Kutepov, A.M. (1987) Stochastic Analysis of Hydro-Mecha-Nical Processes of Separation of Heterogeneous Systems. Theoretical Foundations of Chemical Engineering, 21, 147-153.
NOTES

*Corresponding author.


