Journal of Water Resource and Protection
Vol.5 No.1(2013), Article ID:27101,8 pages DOI:10.4236/jwarp.2013.51006
Tritium/Helium-3 Dating of River Infiltration: An Example from the Oderbruch Area, Berlin, Germany
Physics Department, Faculty of Science, Assiut University, Assiut, Egypt
Email: elgamal99@yahoo.com
Received November 5, 2012; revised December 5, 2012; accepted December 13, 2012
Keywords: Groundwater Dating; Bank Infiltration; Excess Air
ABSTRACT
The concentrations of tritium, helium isotopes and neon have been measured in groundwater samples from a shallow and deep groundwater system recharged by bank infiltration from the Oder River in northeastern Berlin, Germany. The apparent 3H/3He ages show a distinct variation. They increased from only a few months to >40 years along the flow path. The farthest wells from the river have high concentration of 4He terrigenic which is around 5 × 10−5 (ccSTP/kg). The highest values for stable 3H (3H + 3Hetrit) were encountered at a 2.6 km distance from the river.
1. Introduction
Both tritium and helium isotopes have been used as environmental tracers of groundwater flow in a variety of hydrogeologic settings. The 3H/3He ratio has been used successfully in dating groundwater less than 50 years old [1-4], while 4He has been used to quantify groundwater flow rates at both long [5] and intermediate travel times [6]. These studies focused either on the use of the 3H/3He ratio or on the use of 4He in their investigations. Although 4He must be measured along with 3He in order to determine the nontritiogenic amount of 3He [7], the concentration of 4He does not tend to be used in the interpretation of groundwater flow patterns.
In this paper, the 3H/3He dating method [1,8] was used to determine the travel time of groundwater to the monitoring screen. 3H/3He groundwater dating is based on the radioactive decay of tritium and the containment of the decay product 3He in groundwater. 3H/3He directly yields a travel time and can be applied to a single sample, whereas 3H alone requires a depth profile to locate the 3H-bomb peak [1]. Groundwater travel times were determined from 3H and 3He samples collected in 2001 and measured by the Bremen Mass Spectrometric Facility for the measurement of helium isotopes, neon, and tritium in water [9]. The groundwater travel times were calculated based on the ratio between tritiogenic helium and tritium [1,8,10,11] according to:
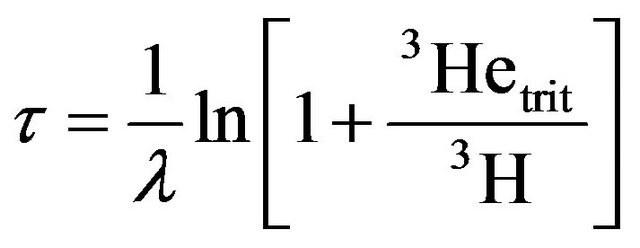 (1)
(1)
where λ = 0.0556 yr–1 is the decay constant of 3H and [3H] is the measured tritium concentration. It is usually expressed in tritium units (TU). 1 TU corresponds to a 3H/1H ratio of 10–18. [3Hetrit] is defined as the fraction of the total 3He produced by 3H decay. It was calculated by the difference between the measured concentration [3Hemeas] and the concentrations of all other 3He components: [3Heeq]: equilibrium, [3Heexc]: excess air, and [3Heterr]: terrigenic
3Hetrit = 3Hemeas – 3Heeq – 3Heexc – 3Heterr (2)
The equilibrium concentration in water [3Heeq] is determined by the water temperature and the ambient air pressure (altitude) during recharge. Solubility data for He and Ne isotopes are taken from Weiss (1970) [12] and from Benson and Krause (1980) [13]. The atmospheric excess [3Heexc] can be calculated from the Ne or from the 4He excess, provided that the latter is exclusively of an atmospheric origin. Isotopic and elemental compositions of the atmosphere are taken from Ozima and Podosek (1983) [14]. If the water sample contains 3Heterr, which may be present in aquifers where rocks are enriched in U or Th, or in groundwater samples in which young water has mixed with relatively old water containing terrigenic, and in some cases, mantle He, in these cases, the Ne concentration must be measured and can be used to calculate the additional 3Heterr [15].
4Heterr = 4Hemeas – (Nmeas – Neeq) × (4He/Ne)atm – 4Heeq (3)
where 4Heterr is the terrigenic 4He concentration, Nemeas is the measured neon concentration, Neeq is the neon concentration in water in equilibrium with air, and (4He/Ne)atm is the atmospheric ratio (0.288), then 3Hetrit can be calculated by
3Hetrit = 4Hemeas·Rmeas – (4Hemeas – 4Heterr) × Ra
– 4Heeq × (Ra – Req) – 4Heterr × Rterr (4)
where Ra is the atmospheric 3He/4He, Req = αRa, α is a fractionation factor of about 0.983 [13] and Rterr is the average 3He/4He production ratio in crustal rocks of 2 × 10–8 [16].
The 3He/4He and 4He/Ne ratios are usually assumed to be atmospheric; this assumption is not completely right, because of the measurements of noble gases in paleo groundwater shows that excess air can be fractionated relative to atmospheric air [17].
2. Hydrogeology of the Field Sites
The Oderbruch is the Germany’s largest enclosed river polder area. It is located in eastern Brandenburg at the Border to Poland; about 50 km north east of Berlin and it covers an area of more than 800 km2 (Figure 1). The region has been artificially drained during the past 250 years. Melioration activities included the redirection of the former riverbed further towards the east, the installation of an extensive drainage ditch and pumping station system and the building of a levee along the entire river. Today, as a result of the initiated changes, a major part of the region lies below the river water table. The steep hydraulic gradient between the water table of the Oder River and the aquifer results in the permanent lateral infiltration of river water into the shallow upper aquifer, which is confined along the riverbanks. An overview on the hydraulic situation with the drainage-ditch system and the groundwater potentials is given in Figure 2.
The Bahnbrueke field-site is a 1 km2 and is located adjacent to the Oder River in the northern Oderbruch (Figure 1). Major hydrological features, schematically shown in (Figure 2), include the river, the dike at about 50 - 100 m distance from the river and the main draining ditch further inland at about 150 m distance from the

Figure 1. Location of the Oderbruch river polder including the field site “Bahnbrueke”.
river, all running parallel to one another. The potentiometric surface shows steep gradients directed to the polder centre. During the first 500 m distance, the gradient decreases rapidly due to the pressure release from drainage. The groundwater shows high upward gradients in the direction towards the drainage channel. There are 26 conventional piezometers and 2 multilevel wells were installed at Bahnbrueke in 1999 at a distance of 3 to 620 m from the river. The screen depths are either shallow (3 - 8 m below ground) or deep (15 - 21 m below ground). Further inland, several piezometers were built in flow direction up to a distance of 5 km from the Oder.
The Oder River is 200 m wide and relatively shallow (1 - 2 m). The river base is highly permeable and consists of coarse-grained sands and gravel (kf = 1.0 - 1.7 × 10–3 m·s–1) [18]. Hence, the hydraulic contact between river and groundwater is unrestrained.
The aquifer is of Pleistocene glaciofluvial origin and on average about 20 - 30 m thick [19]. It consists of fine to medium sized sands which get coarser and more gravelly towards the base above the underlying till (Figure 3).
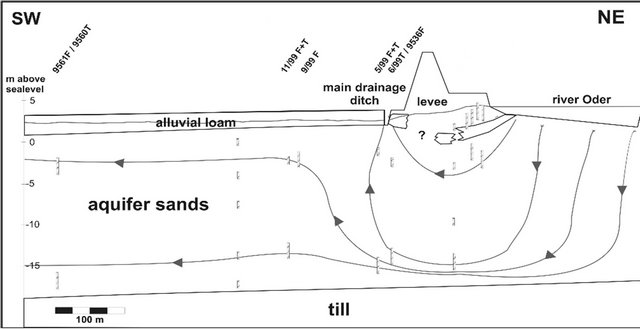
Figure 2. An overview of the hydraulic situation with the drainage-ditch system and the groundwater potentials (updated from Massmann, 2002 [18]).

Figure 3. Geological cross-section of Oderbruch area based on data of various geological investigations.
The hydraulic permeability is in the range of 5.5 × 10–5 to 1.8 × 10–3 m·s–1 [18]. Very thin (cm-range) layers of impermeable silts or clay may exist within the aquifer but have no effect on the hydraulic regime. The thickness of the overlying alluvial or flood plain loam varies from 0.2 to 4.0 m. The loam is clayey, sometimes sandy organic rich silt with strong variations in the hydraulic conductivity.
The bank filtrates to a large extent into the main drainage ditch running parallel to the levee at 100 - 200 m river distance. More than 80% of the infiltrate is discharged into this ditch. Flow velocities between river and ditch generally lie between 0.5 and 1.5 m·day–1 but can be as high as 5 m·day–1 locally. The bottom of the main drainage ditch is highly heterogeneous. It can be covered with up to 2 m of clayey silt or organic rich hydrous sediment while at some locations, the ditch cuts directly into the aquifer sands. Because of its heterogeneity, the efficiency of the ditch varies strongly, resulting in even more complicated flow patterns [18].
The groundwater is confined up to 2 - 3 km inland and, depending on the river water level, artesian for the first 300 m. The hydraulic situation in the central polder strongly deviates from the situation near the river. The groundwater is largely unconfined. Recharge through the soil is generally rather small values around 50 - 70 mm·a–1 and largely inhibited by the impermeable loam. However, human interference due to the levee construction, agriculture (ploughing) and lowering of groundwater levels have reduced the clay content of the soil. Drainage activities have reportedly caused volume changes in the soils due to shrinking, leading to morphological texture changes which influence the recharge rates since precipitation might percolate quickly along shrinking fissures, circumventing the primary pore system [20].
3. Sample Collection and Measurements
Seventeen samples of surface water and groundwater were collected for analysis of helium and neon isotopes in the study area. The samples were collected in special pinch-off copper tubes (containing about 40 cc of water, and fitted with stainless steel pinch-off clamps at each end). The copper tube was fixed in an aluminum channel holding the stainless steel pinch-off clamps. By closing the clamps, the copper tube was shut absolutely gas tight and it was stored till the time of measurement.
Water samples were analyzed for helium (He) and neon (Ne) isotopes at the noble gas laboratory of the Institute of Environmental Physics, University of Bremen. In the laboratory, the copper tubes were connected to a high vacuum system and permanent gases were separated from water and stored in glass ampoules. Leak checks and residual gas checks assured transfer efficiency greater than 99.9%. The glass ampoules were opened in a high vacuum inlet system. Water vapor transferred gases to a cryo system kept at 25 K to separate Ne from other gases. 20Ne and 22Ne were analyzed with a quadrupole mass spectrometer (Balzer QMG112A). Overall calibration with air aliquots and internal water standards assured accuracies for Ne concentrations in water higher than 1.0%. The 1r-standard deviation of 22Ne/20Ne was less than 0.2%. For most samples double measurements were conducted. More details on the measurement techniques can be found in Sültenfuβ et al. (2004) [9].
Tritium samples were collected in 1 litre glass bottles and were extracted from water samples by the gas extraction system described by Sültenfuß et al. (2004) [9]. The extraction efficiency of the system is at least 99.95%. The degassed water was flame sealed in glass bulbs, which were stored in a freezer for nearly four weeks until a sufficient amount of tritiogenic 3He had accumulated to allow determination of tritium content by the 3He-ingrowth method. More details on the measurement techniques can be found in Sültenfuβ et al. (2004) [9].
4. Results and Discussion
4.1. 4He and Ne Concentration
The observed 4He and Ne concentrations (Table 1) appear to have two major sources: 1) gas exchange between river water and the atmosphere, resulting in gas concentrations close to the solubility equilibrium with the atmosphere for the river water temperature; and 2) complete dissolution of small air bubbles possibly caused by water table fluctuation in the recharge area (“excess air”, [21]). Figure 4 shows that some samples have considerable excesses of both noble gases relative to the solubility equilibrium with the atmosphere under conditions typical for the aquifer. Most data point fall on or near the line that represents addition of excess air with an atmospheric Ne/He ratio such as 9560T and 5/99F (the labels T and F respectively describe the deep and shallow wells of the study area). This strongly indicates that excess air component is not fractionated [11].Several samples are marked by additional 4He component of terrigenic origin such as wells 2144F, 2144T, 955F, 955T, 1/01T and 2/01T (Figures 4 and 5).
The analysis of 4He components (Figure 4) shows that the portion of additionally enclosed air (excess air) amounts is less than 20%. The nearest wells from the river (<1000 m) have very small portions of 4He terrigenic and sometimes zero 4He terrigenic concentration (Table 1). The zero values of 4He terrigenic concentrations appear in calculations as a negative values reflect that assumption of excess air formed by complete dissolution of small air bubbles trapped in the soil during infiltration, and therefore composition of excess air is identical to air, is not significant in most cases and the He/Ne ratio of excess
Table 1. Tritium, Helium, Neon Data, and calculated 3H/3He Ages (*NM: Means not measured).
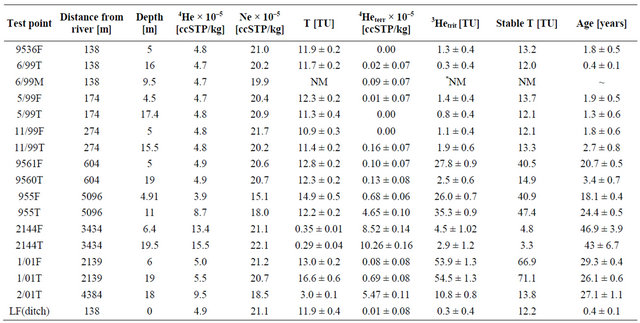
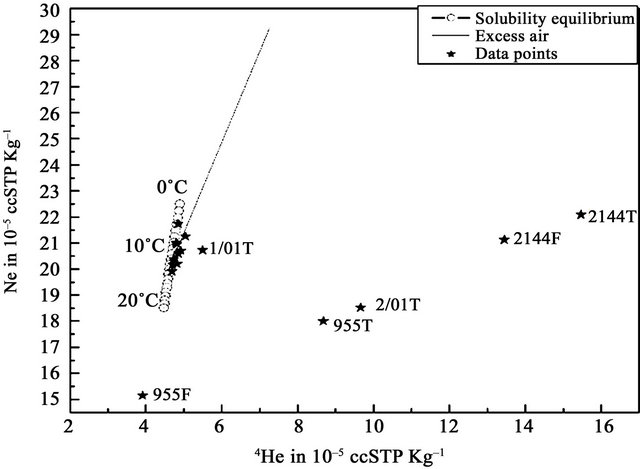
Figure 4. Neon concentration in 10–5 ccSTP/kg versus helium concentration in 10–5 ccSTP/kg.The circle line represents water in solubility equilibrium with atmosphere for a temperature range of 0˚C to 20˚C. The solid line represents excess air at 10˚C.

Figure 5. The analysis of 4He components for the study area.
air is not equal to the atmospheric value of 0.2882. Instead, it is lower, and to determine the appropriate value of He/Ne ratio additional information from other noble gases concentrations is needed. In the recent study only He and Ne data are available so that the assumption of zero concentration of 4He terrigenic is considered to facilitate the calculation of 3He tritiogenic by Equation (4).
Only the furthest wells from the river (2144T, 214 Fand 2/01T) contain a high portion of 4He terrigenic whether these wells are shallow or deep. For these wells Equation (4) was used to calculate 3He tritiogenic. In general, some of the young water samples (<5 years, <1000 m) have zero 4He terrigenic and some others have very small quantities of 4He terrigenic, when compared to the concentration of solubility equilibrium. Some of the 20 - 30 years old samples contain high quantities of 4He terrigenic but less than that of the very old sample >40 years.
4.2. Tritium/3He Data
The calculated 3H/3He ages show distinct variation with distance from the river (Figure 6). The samples from the nearest wells from the river (<1000 m) have ages less than five years. Only the samples from the well 9561 not verify this situation because this is a shallow well inland of the water divide where the flow stagnates, the water flows into the ditch and inland of the ditch it gets very slow. Then the groundwater ages increase nonlinearly with increasing the distance from the river. The highest ages are those of wells 2144T and 2144F, which are located 3434 m from the river. Although, the well 2/01T is the furthest well from the river it has an age 27.1 year this because the water in this well was mixed with water from another sources other than bank filtration.
The initial tritium or stable tritium (3H + 3Hetrit) is plotted versus the calculated 3H/3He ages (Figure 7), where three clearly separated regimes can be recognized: 1) Young water (<5 years) with tritium concentrations of 10 - 15 TU; 2) Old water aged 20 - 30 years with tritium concentrations of 40 - 70 TU. Only the water sample from the well 2/01T has an age from 20 - 30 years but with a tritium concentration from 10 - 15 TU; and 3) 45 years old water with a tritium concentration less than 5 TU.
In case of low water ages (<5 years) and approximately constant 3H concentrations, and if He/3H  1, Equation (1) can be linearized using Taylor expansion to the first order to give:
1, Equation (1) can be linearized using Taylor expansion to the first order to give:
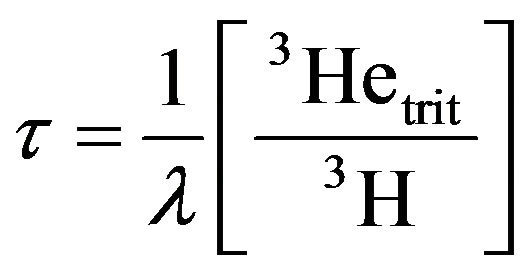 (5)
(5)
The 3He tritiogenic is related linearly to the calculated 3H/3He ages only for water ages less than five years (Figure 8); in this case the age error induced by the measured 3H is negligible. In general, the age errors were calculated using the methods of error propagation and it is mainly caused by the errors of 3He/4He ratio and the concentration of He and Ne. The error of both of them is 1% of its measured values.

Figure 6. The calculated 3H-3He ages against distance from the river Oder.
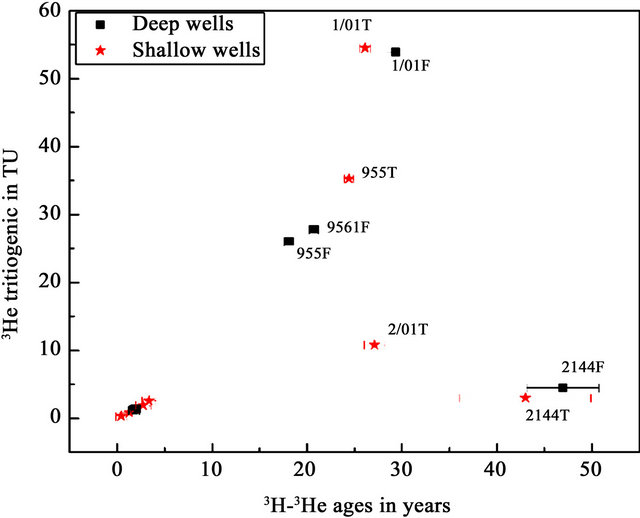
Figure 7. Initial (stable) tritium in TU against the calculated 3H-3He ages in years.

Figure 8. The calculated 3H-He ages against 3He tritiogenic.
The main point of the calculated 3H/3He ages of some samples is that they definitely are the result of mixing of water from different sources other than bank filtration, which have different tritium and 3He concentrations. The 3H/3He ages of a mixture of different water parcels is not a linear function of the ages of the individual parcels, especially if they have different tritium concentrations [22]. The addition of pre-bomb water virtually free of both tritium and tritiogenic 3He would only dilute the concentrations of tritium and tritiogenic 3He, but wouldn’t alter their ratio. Therefore, the 3H/3He ages of the mixture would be the same as that of the young, tritium bearing component. In general the 3H/3He age of mixture deviates from the true mixing age towards the component with the higher tritium concentration [11].
Mixing has significantly influenced the 3H/3He ages from groundwater samples, which can be noticed by comparing the reconstructed original tritium content of the water samples (initial tritium) with historical records of the tritium concentration in precipitation, the tritium records from the IAEA (International Atomic Energy Agency) network are used to do this comparison.
The data points from the sampling location in Oderbruch area are superimposed on the input function (Figure 9) in the following ways:
1) If the water infiltrated with the tritium contents as described by the input function, and subsequently were not influenced by mixing, all initial tritium points should fall on the input curves. The samples, which have 3H/3He ages less than five years, fall on the input curve, these samples have initial tritium concentrations of 10 - 15 TU and the infiltration time is from 1998-2002. Also, we can notice that some samples, which have ages from 20 - 30 years (9561F, 1/01T and 1/01F) fall on the input curves. This means that these samples were not influenced by mixing.
2) If the initial tritium falls below the input curves this means that the groundwater was mixed by an additional input of younger seepage water. The sample from well 2/01T, which has an age of 27.1 years, was mixed by young water infiltrated through the fissures in the alluvial loam. These fissures are formed as a result of the hydraulic situation and the transition from confined to unconfined conditions, which cause the loam to dry out and form fissures [18].
3) The sample from well 2144F falls below and before the input curves, which means, this sample was formed in a pre-bomb era and it has an age greater than 45 years. The initial tritium concentration of this sample is nearly 5
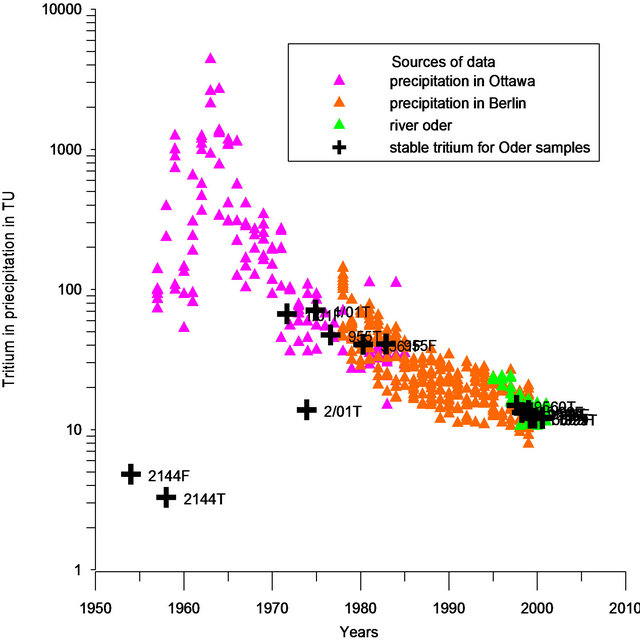
Figure 9. Comparison of the initial tritium concentration and the input function.
TU, which fulfilled the result deduced by Kaufman and Libby in 1954 [23]. The sample from well 2144T falls below the input curves but one can consider that the sample from this well was also formed in a pre-bomb era and not affected by mixing this because it is in the range of its calculated error. The samples from wells 2144T and 2144F are characterized by a relatively high component of 4He terrigenic, which is a good indication of the presence of a significant component of old water.
The samples from wells 955T and 955F locate in the unconfined area like the well 2/01T, so one can assume that the samples from these wells are mixed with young water like that for 2/01T and one can expect that it should also fall below the input curves. But the initial tritium points for these samples fall on the input curves, which gives a bad indication of whether these samples were mixed or not. The calculated 3H/3He ages of these two samples are misleading ages and also their initial tritium, this is because they are highly degassed as a result of formation of H2S in the aquifer due to sulfate reduction [18].
5. Conclusions
This study describes the time scales of groundwater systems in the location Oderbruch area northeastern Berlin, Germany by using the 3H/3He method. This study demonstrates that 3H/3He dating method provides valuable information on the recharge dynamics and residence time of a river bank infiltration on the groundwater system. It also provides valuable information for the management of the water resources.
The assumption of excess air formed by complete dissolution of small air bubbles trapped in the soil during infiltration, and therefore the composition of excess air is identical to air, sometimes leads to negative concentrations of 4He terrigenic. This means that this assumption is not significant in most cases and the He/Ne ratio of excess air is not equal to the atmospheric value of 0.2882. Instead, it is lower, and to determine the appropriate value of He/Ne ratio additional information from other noble gases concentration is needed. In the recent study only He and Ne data are available so that the assumption of zero concentration of 4He terrigenic is considered to make calculations.
The calculated 3H/3He ages for water samples show distinct variation, where some samples have very young water less than five years, some others have water of ages 20 - 30 years. These samples have a part which mixed with young water from different sources. The effects of mixing can be discussed by comparing the reconstructed initial tritium (3H + 3He) content of samples with the temporal evolution of tritium in precipitation. The last set of samples is water with ages greater than 40 years. These samples only occurred in the large distances from the Oder River and one can expect these waters were formed before the hydrogen bomb test and have initial tritium of approximately 5 TU.
The occurrence of a high 4He terrigenic in the groundwater samples gives a good indication to the presence of a significant component of old water.
The infiltration temperature, which was used to determine the equilibrium components of He and Ne is required to apply the 3H/3He method. If the infiltration temperature is unknown, additional noble gases measurements other than He and Ne are required to determine the infiltration temperature. This might be one of the disadvantages of this method. One clear disadvantage of this method is the degassing process, which perhaps occurred during the sampling process or as a result of other gases like H2S or CO2 in the aquifer. This process leads to a misleading age like the samples from wells 955T and 955F in the study area.
6. Acknowledgements
I would like to thank Dr. J. Sueltenfuss for measuring 3H, He and Ne samples in the Institute of Environmental Physics, University of Bremen. My deep thanks to Prof. Dr. G. Massmann, in the Institute of Hydrogeology at Free University of Berlin, for supporting me with the hydrogeological information about the study areas. She also offered significant advice during the interpretation of my results.
REFERENCES
- P. Schlosser, M. Stute, C. DÖrr, C. Sonntag and K. O. Münnich, “Tritium/3He-Dating of Shallow Groundwater,” Earth and Planetary Science Letters, Vol. 89, No. 3-4, 1988, pp. 353-362. doi:10.1016/0012-821X(88)90122-7
- B. Ekwurzel, P. Schlosser,W. M. Smethie, L. N. Plummer, E. Busenberg, R. L. Michel, R. Weppernig and M. Stute, “Dating of Shallow Groundwater: Comparison of the Transient Tracers 3H/3He, Chloroflourocarbons, and 85Kr,” Water Resources Research, Vol. 30, No. 6, 1994, pp. 1693-1708. doi:10.1029/94WR00156
- A. Szabo, D. E. Rice, L. N. Plummer, E. Busenberg, S. Drenkard and P. Schlosser, “Age Dating of Ground Water Using Chlorofluorocarbons, Tritium/Helium: 3, and Flow Path Analysis in an Unconfined Aquifer of the New Jersey Coastal Plain,” Water Resources Research, Vol. 32, No. 4, 1996, pp. 1023-1038. doi:10.1029/96WR00068
- L. N. Plummer, E. Busenberg, S. Drenkard, P. Scholosser, B. Ekwurzel, R. Weppirnig, J. B. McConnell and R. L. Michel, “Flow of River Water into a Karstic Limestone Aquifer. 2. Dating the Young Fraction in Groundwater Mixtures in the Upper Floridan Aquifer near Valdosta, Georgia,” Applied Geochemistry, Vol. 8, 1988, pp. 1017- 1043.
- E. Mazor and A. Bosch, “Helium as a Semi-Quantitative Tool for Groundwater Dating in the Range of 104 to 108 Years,” In: Isotopes of Noble Gases as Tracers in Environmental Studies, International Atomic Energy Agency, Vienna, 1992, pp. 163-178.
- D. K. Solomon, H. Hunt and R. J. Poreda, “Source of Radiogenic Helium 4 in Shallow Aquifers: Implications for Dating Young Ground-Water,” Water Resources Research, Vol. 32, No. 6, 1996, 1805-1813. doi:10.1029/96WR00600
- D. K. Solomon and P. G. Cook, “3H and 3He,” In: P. Cook and A. L. Herczeg, Eds., Environmental Tracers in Subsurface Hydrology, Kluwer Academy, Norwell, 2000, pp. 397-424.
- I. N. Tolstikhin and I. L. Kamenskiy, “Determination of Groundwater Ages by the T-3He Method,” Geochemistry International, Vol. 6, 1969, pp. 810-811.
- J. Sültenfuß, W. Roether and M. Rhein, “The Bremen Mass Spectrometric Facility for the Measurement of Helium Isotopes, Neon, and Tritium in Water,” IAEA, Vienna, IAEA-CN-119/7, 2004.
- D. K. Solomon, R. J. Poreda, S. L. Schiff and J. A. Cherry, “Tritium and Helium 3 as Groundwater Age Tracers in the Borden Aquifer,” Water Resources Research, Vol. 28, No. 3, 1992, pp. 741-755. doi:10.1029/91WR02689
- W. Aeschbach-Hertig, P. Schlosser, M. Stute, H. J. Simpson, A. Ludin and J. F. Clark, “A 3H/3He Study of Groundwater Flow in a Fractured Bedrock Aquifer,” Ground Water, Vol. 36, No. 4, 1998, pp. 661-670. doi:10.1111/j.1745-6584.1998.tb02841.x
- R. F. Weiss, “The Solubility of Nitrogen, Oxygen and Argon in Water and Seawater,” Deep Sea Research, Vol. 17, 1970, pp. 721-735.
- B. B. Benson and D. Krause, “Isotopic Fractionation of Helium during Solution: A Probe for the Liquid State,” Journal of Solution Chemistry, Vol. 9, No. 12, 1980, pp. 895-909. doi:10.1007/BF00646402
- M. Ozima and F. A. Podosek, “Noble Gas Geochemistry,” Cambridge University Press, Cambridge, 1983.
- R. Bayer, P. Schlosser, G. Bönisch, H. Rupp, F. Zaucker and G. Zimmek, “Performance and Blank Components of a Mass Spectrometric System for Routine Measurement of Helium Isotopes and Tritium by the 3He in Growth Method,” Sitzungsber der Heidelberger Akademie der Wissenschaften, Mathematisch Naturwissenschaftliche Klasse, Jahrgang Springer Verlag. 5, 1989, pp. 241-279.
- B. A. Mamyrin and I. N. Tolstikhin, “Helium Isotopes in Nature,” Elsevier, Amsterdam, 1984.
- M. Stute, M. Forster, H. Frischkorn, A. Serejo, J. F. Clark, P. Schlosser, W. S. Broecker and G. Bonani, “Cooling of Tropical Brazil (58˚C) during the Last Glacial Maximum,” Science, Vol. 269, No. 5222, 1995, pp. 379-383. doi:10.1126/science.269.5222.379
- G. Massmann, “Infiltration of River Water into the Groundwater Investigations and Modelling of Hydraulic and Geochemical Processes in the Oderbruch Aquifer, Germany,” Ph.D. Disseration, Free University, Berlin, 2002.
- M. Hannemann, “Neue Ergebnisse zur Relief Gestaltung, Stratigraphie und glazigenen Dynamik des Pleistozaens in Ostbrandenburg,” Ph.D. Disseration, Humboldt University, Berlin, 1966.
- G. Massmanna, A. Pekdegera and C. Merzb, “Redox Processes in the Oderbruch Polder Groundwater Flow System in Germany,” Applied Geochemistry, Vol. 19, No. 6, 2004, pp. 863-886. doi:10.1016/j.apgeochem.2003.11.006
- T. H. E. Heaton and J. C. Vogel, “Excess Air in Groundwater,” Journal of Hydrology, Vol. 50, 1981, pp. 201-216. doi:10.1016/0022-1694(81)90070-6
- W. J. Jenkins and W. B. Clarke, “The Distribution of 3He in the Western Atlantic Ocean,” Deep Sea Research, Vol. 23, 1976, pp. 481-494.
- S. Kaufman and W. F. Libby, “The Natural Distribution of Tritium,” Physical Review, Vol. 93, No. 6, 1954, pp. 1337-1344. doi:10.1103/PhysRev.93.1337

