Received 25 January 2015; accepted 13 February 2015; published 15 February 2015

ABSTRACT

The cross-gradients joint inversion technique has been applied to multiple geophysical data with a significant improvement on compatibility, but its numerical implementation for practical use is rarely discussed in the literature. We present a MATLAB-based three-dimensional cross-gradients joint inversion program with application to gravity and magnetic data. The input and output information was examined with care to create a rational, independent design of a graphical user interface (GUI) and computing kernel. For 3D visualization and data file operations, UBC-GIF tools are invoked using a series of I/O functions. Some key issues regarding the iterative joint inversion algorithm are also discussed: for instance, the forward difference of cross gradients, and matrix pseudo inverse computation. A synthetic example is employed to illustrate the whole process. Joint and separate inversions can be performed flexibly by switching the inversion mode. The resulting density model and susceptibility model demonstrate the correctness of the proposed program.

Keywords:

Joint inversion, Cross gradients, Gravity and magnetic data, Numerical implementation, Graphic user interface

1. Introduction

The 3D joint inversion (i.e., imaging) technique of multiple geophysical data often reveals a subsurface structure more accurately than an individual inversion of single dataset. The joint inversion process relies on a certain linkage among various models, for which several methodologies have been proposed [1] - [7] . One conventional scheme takes sample property measurements when available, and determines their statistical interrelationships to restrict the inversion process. Unlike this, structural link methods are widely used to perform joint inversion without requiring rock property data. The cross-gradients technique is one such method, and its structural similarity criterion has been shown to give good results [8] . First proposed by Gallardo and Meju [9] , the method was based on the assumption that, although petrophysical correlation varies, implicitly common bound- aries exist. The method has been successfully applied to both synthetic and real data, but the relevant numerical implementation for practical use has rarely been discussed in previous work.

We now present a simple and general numerical implementation of 3D cross-gradients joint inversion frame- work for gravity and magnetic data in the MATLAB programming environment, noted for its powerful scientific computing capability (especially for matrix solution) and its graphical utilities. First, the joint inversion theory is briefly reviewed, and the separate design of a graphical user interface (GUI) and computing kernel is analyzed. Second, some key issues concerning numerical emplementation are discussed (e.g., forward difference of cross- gradients, and matrix inverse computation). A synthetic joint inversion experiment was carried out to demon- strate the basic use of the proposed program. A comparative example is presented to indicate the practicality of the program.

2. General framework of cross gradients joint inversion

2.1. Inputs and outputs

Generally, an inversion converts acquired geophysical data into a physical property model, which is then as- signed geological information to explain the nature of the subsurface material or its geological structure. Cross- gradients joint inversion uses two or more types of data to reproduce physical models. This is often found to be more accurate than dealing with each data type separately because of the constraints offered by the additional structural information. Figure 1 shows the basic input and output of a cross-gradients joint inversion of gravity and magnetic data. This data is obviously necessary for the inversion to be carried out, but other information― reference models, boundary constraints and inversion parameters needed to control the procedure―is optional. The standard output comprises 3D density and susceptibility distribution and their corresponding predictions.

The input and output (I/O) dataset is usually stored as observational data, configurations and 3D model files. A commonly adopted approach to organizing such datasets is to use the University of British Columbia Geophysical Inversion Facility (UBC-GIF) format (ASCII encoding) [10] . In this format, observational data is arranged in columns along with observation locations and estimated errors. The models are ordered and sorted into columns with the associated mesh configuration file. To handle the frequent use of the I/O operations of these file formats, several MATLAB functions are written (listed in Table 1). These import the revelant datasets that are then processed utilizing a computing kernel module (described below). UBC-GIF tools are again invoked by these functions to export files and 3D graphics of the resultant models and predictions.

a. For more information about UBC-GIF tools, please refer to [10] .

2.2. Graphical user interface design

Cross-gradients joint inversion involves different kinds of observed data, different physical models and various choices of inversion parameters, all of which may cause confusion to users and make the program difficult for them. Some inversion parameters, such as regularization and the structural coupled factor, are usually chosen by trial and error; however, the results may be distorted if incorrect parameters are used, neccessating a data experiment before the inversion is performed. A GUI has been designed to encourage users to perform easy inversions and data experiments without confusion [11] .

Figure 2 shows the main interface of this program. The files and their corresponding parameters need to be completed in the editing box controls on the panel. Four graphical box controls display inversion data during processing (blank while initializing). All the available operations are arranged as menu bars above the panel.

The inversion parameters and input file directions are recorded by a customized project file that can be either loaded or saved using the first menu item Project. The View menu is used to visualize the observational data or the 3D models using UBC-GIF tools, which produce 3D visuals of higher qualitythan the built-in MATLAB functions. The Inversion menu contains two modes―joint inversion, and separate inversion without structural constraints. The Tests menu helps the user to carry out data experiments and assists in the selection of correct inversion parameters such as depth weighting and regularization. Finally, the Help menu is linked to a user’s manual and an About dialogue box. There is also a status bar displaying the local time and current state of the program.

2.3. Compute-intensive module design

The computation kernel module has been designed to be separate from the GUI for its strict requirement of computing resources, including the CPU loadings and memory allocations. Following Fregoso and Gallardo [8] , the inversion equation may be expressed with some slight modification as:

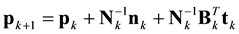, (1)

where

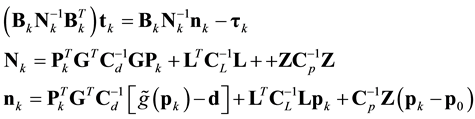. (2)

Here subscript k denotes the iteration number; 0 is a priori information; d is a data vector; p is a model vector transformed from property model m (in combined manner); matrix Z is a weighting matrix; L is a Laplacian matrix; C is a covariance matrix with respect to subscript d, L and p, which indicate data, smoothness and smallness terms; t is a column vector of assembled cross-gradients components in 3D space; B is a Jacobian matrix of cross-gradients; and P is a Jacobian matrix of transform function. The final models m₁ and m₂ are extracted from p by the inverse transform function when the iteration procedure satisfies the given data and structural misfit thresholds. For more details of Equation (1), please refer to [8] . The parameters (Table 2) to be assigned in the GUI partly constitute the arrays described above. The cross-gradients joint inversion procedure for this iterative scheme is illustrated in Figure 3.

There are several key considerations when numerically implementing the iterative Equation (1). First, the gradient operator involved in t, L and B must be calculated in a 3D difference scheme, preferably by using forward differences to eliminate the chessboard pattern [12] . The discretization of t_x, t_y and t_z are, from [8] .

, (3)

where subscripts x, y, z denote the cell adjacent to the center in each direction, and c is the center cell (Figure 4). The exact value of B is difficult to compute directly, but by discretizing t, an approximate value is obtained by a Taylor’s expansion of the cross gradients at the zero point and neglecting the higher orders. For most cases, t takes a value close to zero, so the approximate solution is always sufficiently precise (the reader is referred to [8] [9] for more details). Note that, since the computation for each element is independent, it is suggested that the code be vectorized in order to utilize the full potential of MATLAB’s matrix computing capability [13] [14] . A built-in function “sparse” is employed to perform efficient assembling of these matrices [15] .

Second, matrix N is inverted by a standard inverse algorithm when its condition number is not too large; fortunately, matrix C_p plays a regulator role to eliminate the ill-conditioned problem [16] . It can generally be solved by the standard inverse solver “inv” with high precision, but the inverse of the composed matrix [BN⁻¹B^T] is usually difficult to compute because the production of several of the involved matrices makes it singular. In previous work, truncated singular values decomposition (SVD) has been used to calculate the pseudo inverse [8] ; however, here we prefer to resolve the problem using a damped least-squares technique in which a damping factor is introduced:

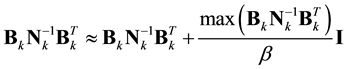. (4)

where I is the identity matrix, and β is a structural coupling factor. The second term on the right-hand side of Equation (4) in effect makes the total matrix well-posed. Taken together with the composed array [BN⁻¹n-t] on the right-hand side, a linear system emerges which may be solved using the built-in CG solver “bicg” [15] .

3. Synthetic example

A synthetic experiment was carried out to illustrate the basic use of this program. The whole standard iterative process is shown in Figure 5. The textboxes are locked until the process is complete. The gravity and magnetic data (Figure 6) are generated on a synthetic geological model (Figure 7), and with 2.5% Gaussian noise added. The model consisted of two anomalies, A and B, with density contrast 0.5 g/cm³, 1 g/cm³ and susceptibility 1 (SI unit, similarly hereinafter) and 0.5, respectively. The mesh comprised 20 × 20 × 10 regular prisms of 50 m side length. All of the observed and geometry data were collected into the relevant files. The depth weighting parameters were chosen by UBC-GIF tools [10] , and the regularization parameters were selected by trial and error aided by L-curve optimization [16] .

When the process was complete, the View menu invoked UBC-GIF tools to visualize the resulting models and data shown in Figure 6 and Figure 7. It is seen that the inverted density model and susceptibility model reproduced the data very well, indicating the accuracy of the fitting feature of this process. When compared to the true density and susceptibility models, the recovered values reflected the relative amplitude and locations correctly.

To demonstrate the significant improvement produced by joint inversion, we also conducted a comparative experiment by changing the inversion mode parameter from joint to separate. The recovered models are shown in Figure 8, which show that the anomalies were recovered in the correct location but with low resolution. Note that the boundary between the two anomalies is blurred, making it hard to identify the two independent targets in the separate images.

4. Conclusion

A MATLAB-based numerical implementation of cross-gradients joint inversion of gravity and magnetic data is presented. A user-frendly GUI has also been designed for flexible handling of multiple observations, models and inversion control parameters. The inversion process is carried out using an independent module. Some important issues are discussed, such as cross-gradients computing and matrix inverting. The use of this program has been illustrated by a simple example using synthetic data. The correctness and accessibility of this program have been demonstrated. Although this program is available for both research and practical use, we suggest porting this MATLAB-based program to other professional software platforms (e.g., ArcGIS) for more integrating and convenient applications in the future work.

Acknowledgements

This work was funded by National Natural Science Foundation of China, Beijing Higher Education Young Elite Teacher Project (YETP0650), The National High Technology Research and Development Program (“863” Program) of China (No. 2013AA063901-4 and 2013AA063905-4), R & D of Key Instruments and Technologies for Deep Resources Prospecting (The National R&D Projects for Key Scientific Instruments) (No.ZDYZ2012-1- 02-04), Constrained multi-parameter inversion of geophysical technology and software systems (No. 2014AA06 A613), and The Fundamental Research Funds for the Central Universities. We thank the UBC-GIF and Roman Shekhtman, the developer of Meshtools3D and gm-data-viewer, for making the programs available to the scientific community.

References

NOTES

^*Corresponding author.