Journal of Software Engineering and Applications
Vol.07 No.10(2014), Article ID:49990,10 pages
10.4236/jsea.2014.710078
Overlapping Community Detection in Dynamic Networks
Nathan Aston, Jacob Hertzler, Wei Hu*
Department of Computer Science, Houghton College, Houghton, USA

*Corresponding author.
Email: *wei.hu@houghton.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 11 July 2014; revised 8 August 2014; accepted 2 September 2014

ABSTRACT
Due to the increasingly large size and changing nature of social networks, algorithms for dynamic networks have become an important part of modern day community detection. In this paper, we use a well-known static community detection algorithm and modify it to discover communities in dynamic networks. We have developed a dynamic community detection algorithm based on Spea- ker-Listener Label Propagation Algorithm (SLPA) called SLPA Dynamic (SLPAD). This algorithm, tested on two real dynamic networks, cuts down on the time that it would take SLPA to run, as well as produces similar, and in some cases better, communities. We compared SLPAD to SLPA, LabelRankT, and another algorithm we developed, Dynamic Structural Clustering Algorithm for Networks Overlapping (DSCAN-O), to further test its validity and ability to detect overlapping communities when compared to other community detection algorithms. SLPAD proves to be faster than all of these algorithms, as well as produces communities with just as high modularity for each network.
Keywords:
Community Detection, Modularity, Dynamic Networks, Overlapping Community Detection, Label Propagation

1. Introduction
In the current world we live, interactions between individuals have become far easier than before due to online media. Massive social networks, such as Facebook, Twitter, and LinkedIn, have allowed individuals to connect with one another on a vast level. These interactions can be modelled with networks by turning the individuals on the network into nodes, and showing their communication between other individuals as edges between nodes, as modelled by Figure 1. Networks can be described as either static or dynamic: a stationary structure or a continually changing structure over time. Nodes from these networks tend to group closely with each other, forming communities. Communities can be described as distinct groups of nodes that are very well connected between other closely related nodes and only loosely connected between other groups of well-connected nodes inside the network.
Communities can take on several different characteristics, ranging from small, such as a close-knit group of friends on Facebook, to large, such as millions of individuals following an international star on Twitter, as well as being able to include several different types of people within the community. Another important aspect of these communities is their ability to overlap. A single node can belong to several different communities, such as a node on Facebook being friends with nodes from a workplace as well as nodes from a sports team, creating more dynamic interaction between communities than what would be allowed otherwise.
Research has produced a variety of methods to analyze these massive networking sites, creating opportunities to study and discover the dynamics, habits, and general rules of social network communities. What are commonly used to study these networks are community detection algorithms, which use various techniques to group and produce collections of nodes that form communities. Algorithms that detect communities in dynamic networks use several snapshots, or timestamps, of the network, taking into account the changes of the network that happen naturally between consecutive timestamps, and from there also produce communities.
In Section 2, we will introduce other community detection algorithms. Some of which we build upon to develop our algorithm, and others we used as baselines on which to test our algorithm. Following this, Section 3 will describe the basic concepts in detecting community structures in dynamic networks. Section 4 is where we describe our contributed algorithm SLPAD. Then to compare the overlapping community detection of our algorithm, Section 5 describes the modifications we made to two other community detection algorithms to allow them to discover overlapping communities. Section 6 introduces the datasets we used to perform community detection and the measures we used to quantify the performance of their discovered communities. Then finally, Section 7 explains the results of our algorithm compared to the baseline algorithms run on the datasets we introduce. Section 8 will conclude this paper.
2. Relate Works
In the pursuit of community detection, there are several algorithms present today that offer a variety of techniques to process networks and find communities. One such algorithm is Label Propagation Algorithm (LPA), which discovers communities by allowing a random node to become a receiver, taking on the most popular label of all its neighbors. If there is a tie between two or more labels, which happens often in the first few iterations, a label is selected at random from them. The process ends when each node’s label does not change, or if the algo-
Figure 1. A network of eight nodes with two communities.
rithm arrives at a user-set number of iterations, and the community membership is determined based on the labels the nodes have received [1] .
LPA can only find disjoint communities, or communities with no overlap. Another algorithm, Speaker-Lis- tener Label Propagation Algorithm (SLPA), uses the same propagation method as LPA, but allows for nodes to hold more than one label, unlike LPA’s one label allowance. This gives nodes the opportunity to be part of more than one community, thus allowing for the detection of overlap [2] .
Another algorithm, LabelRank, uses the idea of label propagation for its community detection, but instead of propagating labels at random, LabelRank uses the probability that a node will receive a label from a neighbor, which removes the randomness that is seen in LPA and SLPA. Due to this avoidance of randomness, LabelRank produces more stable community structures than LPA and SLPA. LabelRank also uses a stop criterion, which ensures a safe termination that also produces good results. The stop criterion, however, does not always guarantee the best runtime, but LabelRank is still very efficient despite this [3] .
LabelRank updates all of its nodes at the same time, which can be inefficient. An algorithm based on LabelRank, LabelRankT, solves this problem by using local operations, working incrementally and only updating nodes that have changed in consecutive timestamps. This allows for greater efficiency, as well as being able to track a community through a change in time, due to its deterministic results [3] .
Another development for community detection in static networks is Structural Clustering Algorithm for Networks (SCAN), derived from DBSCAN (Density Based Spatial Clustering of Applications with Noise). Unlike DBSCAN, which uses distance between nodes to determine community placement, SCAN uses a user-defined threshold ε to determine a node’s neighbors, using this information to incorporate the node into a community. Nodes that share similar neighbors in their ε-neighborhood (the user-defined threshold) can be grouped and formed into a community. SCAN also allows for the detection of hubs and outliers, hubs being nodes that don’t belong to a community, but connect two or more communities, and outliers being nodes outside of communities that have neighbors from only one community [4] .
To detect communities in dynamic networks efficiently, DSCAN (Dynamic SCAN) was created as an improved version of SCAN that, instead of updating the entire network with each iteration, finds the difference in edges between consecutive timestamps, and updates only the nodes involved in the changed edges. DSCAN also no longer requires a user-input for the ε threshold, instead finding an average for ε between the values of 0.4 and 0.8. DSCAN, when dealing with larger communities, tends to perform quicker than SCAN, while at the same time maintaining the same quality of SCAN in modularity, a common benchmark for determining the strength of a community [4] .
Another approach to community detection is based on Genetic Algorithms (GA). GA imitates evolution to find the optimal solution to a problem. GA starts by generating a random population of solutions, measuring each solution’s strength based on a fitness function, then mutating the population to form a new generation of solutions. The process repeats until either the maximum amount of iterations is reached, or an acceptable level for the fitness function has been reached, indicating an optimized solution to the problem at hand. Applying GA to community detection would mean using this same process to develop a community structure that would satisfy a fitness function for community strength [5] .
One algorithm that uses GA for community detection is GA-Net, which uses a system of assigning all the values to genes (which serve as nodes) to form communities. GA-Net starts by randomly generating genotypes for the network, as well as performing a check to make sure each individual can be regarded as safe, meaning there is an edge between the gene and the allele value assigned to it as well as protecting against improper grouping. GA-Net then performs uniform crossover, which creates a random binary vector, then uses that vector to select genes from each parent to pass on to the child. Since both parents are assumed to be safe due to the check, the child can also be assumed to be safe. After this, the fitness function, in GA-Net’s case community score, is computed for each member, and then a new population is created from the old members, eventually converging on a solution to the problem [5] .
3. Community Detection in Dynamic Networks
In a static network, let G = {V, E} be a network where V is the set of nodes and E is the set of edges consisting of node pairs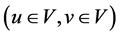 . In a dynamic network, let Gt = {Vt, Et} be a network at timestamp t with Vt and Et being its corresponding node and edge sets respectively.
. In a dynamic network, let Gt = {Vt, Et} be a network at timestamp t with Vt and Et being its corresponding node and edge sets respectively.

Changes in a dynamic network from 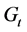 to
to 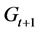 are seen in the changes from
are seen in the changes from 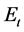 to
to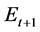 . Any new or removed nodes in
. Any new or removed nodes in 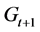 will be connected to an edge, which will be found in
will be connected to an edge, which will be found in 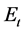 or
or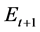 ; if a node does not contain any incident edges, then the community structure of a network would not be affected by the disjoint node. Our approach to community detection in dynamic networks focuses on this idea of updating a community structure around the nodes that have seen edge changes between two consecutive timestamps.
; if a node does not contain any incident edges, then the community structure of a network would not be affected by the disjoint node. Our approach to community detection in dynamic networks focuses on this idea of updating a community structure around the nodes that have seen edge changes between two consecutive timestamps.
4. SLPAD
Our study is based upon the algorithm SLPA and incorporates the ability for this algorithm to handle dynamic networks. We propose the algorithm SLPAD (Speaker-Listener Label Propagation Algorithm Dynamic) which uses SLPA’s label propagation technique to propagate labels only throughout portions of the network, reducing runtime. Algorithm 1 illustrates the pseudo-code for SLPAD.
For each graph Gi, SLPAD obtains the edges, ∆E, that have changed between two consecutive timestamps and acquires all nodes incident to them, ∆V. This set of nodes is then expanded to include all nodes belonging to communities of these nodes. The SLPA algorithm is then run on these nodes, with T as number of iterations and r as the cutoff threshold. Essentially, SLPAD involves running SLPA on communities that change from one timestamp to the next. One condition for the selected listener node is that the only speakers it can receive from must be within the node set that is being updated. In our algorithm, along with the idea of the listener node receiving a random label from a speaker, the speaker can also be able to send their highest frequency label to the listener. This helps the SLPA algorithm converge quicker and produce more stable results when run multiple times.
Before SLPA is run on the nodes that will be updated, two cleanup techniques must be performed. First, labels of nodes that disappeared from the previous timestamp to the current are removed from all nodes in the network. This helps to clean out labels of nodes that no longer exist, because these nodes can no longer propagate their labels through the network. The final step before running SLPA is to reset the labels of the nodes that are about to be updated. This is essentially the initialization phase of SLPA, but only on the nodes that will be updated.
One of the ways SLPAD helps to improve modularity and tighten community structure is by using our community repair function. Community repair works by checking each node’s neighbors and moving that node to the community with the highest neighbor count, effectively making sure that nodes belong to the same community that the majority of its neighbors belong to.
A potential problem for SLPAD is finding the right overlap for a node. If an edge between a node and its community disappears, its degree to the community decreases, which can possibly bring its degree down close to that of a different community. Since SLPAD only updates based on edge changes, a problem can arise from only one community involved in the edge change being updated, which can complicate finding an overlapping node between two communities if only one community of two in a possible overlap is updated. To combat this, we use a simple technique to repair overlapping in SLPAD, which works by finding the nodes attached to removed edges in the network, determining how many neighbors of each community the nodes have, and then deciding which communities the node belongs to.
Due to the large size of many networks, runtime can become a problem for many algorithms. For some algorithms, threading can be used to cut down on this problem. SLPAD allows for threading, where each node can independently ask its neighbors for label’s and obtain the maximum occurring label of the received labels. Threading can also handle the removal of low frequency labels and the community repair of nodes.
5. Overlapping Community Algorithms
For a benchmark on overlapping community detection, we modified two disjoint community detection algorithms and equipped them with the ability to find overlapping community structure. Due to how these two algorithms form communities, performing overlapping discovery was a simple task.
We modified DSCAN to detect overlapping communities, calling the product DSCAN Overlapping (DSCAN- O). To detect nodes that connect overlapping communities, after DSCAN’s community detection, DSCAN-O checks every node and acquires each of their maximum similarity of all incident edges. A user specified similarity-decrease value defines the overlapping threshold. Any node with an edge that is incident to another community with a similarity greater than the node’s maximum similarity minus the similarity decrease becomes part of the other community and signifies overlap between the two communities.
As well as DSCAN-O, we modified LabelRankT to be able to detect overlapping communities. Essentially, when the highest probability label is found, a threshold is introduced, and if any other label is within the highest label probability minus the threshold, the node takes on that label as well. We gave LabelRankT and DSCAN-O very similar overlapping community detection modifications.
6. Dynamic Network Datasets
To test our new algorithm compared to other commonly used algorithms, we employed three real world networks ranging from small to large. The first and largest, the arXiv HEP-TH physics network, is a citation graph that includes 27,770 papers and 352,807 citations between papers. This data in the graph is comprised of papers written between January 1993 and April 2003 [6] . Due to the gradual collection of the papers during the 10 years, we were able to generate timestamps for the graph to test with SLPAD.
The next network, the MIT Social Evolution Call-SMS network, is much smaller than the physics network, being made up of only 80 nodes and 273 edges. In this dataset, nodes are undergraduate students, and the edges between them represent calls or SMS text messages between students. The time period it includes is between October 2008 and May 2009 [7] .
The final network we used is similar to the Call-SMS network described above. The MIT Friends and Family-SMS Network tracks mobile phone usage between individuals. However, unlike the Call-SMS network above, this network only tracks SMS messaging. These interactions were recorded between March 2010 and June 2011 [8] .
For evaluating the effectiveness of communities, we use modularity [9] . Modularity measures the difference between the number of edges found in a community to the expected number of edges in a randomly generated community structure. Modularity can be described as:
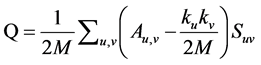
where M is the number of edges, A is the adjacency matrix, kx is the degree of node x, and Suv returns 1 if u and v are in the same community and 0 otherwise. Since our algorithms can detect overlapping communities, we will also use EQ [10] . EQ can be described as:
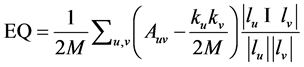
where M, A, and kx are the same, and lx is the set of communities of x. EQ is modularity that evaluates all common communities between nodes. When no overlaps exist in a network timestamp, then EQ is modularity. Both modularity and EQ produce values in the range of 0 to 1, where higher values indicate a better community structure.
7. Results
To test SLPAD, we ran it on the aforementioned networks along with SLPA, LabelRankT, and DSCAN-O. SLPAD ran faster than all three other algorithms and community repair improved modularity when SLPAD without community repair was not enough. All algorithms tested detect overlapping nodes with a slight degree of similarity.
As noted previously, SLPAD provides the option for a listener to obtain either a random label or the most frequent label from a speaker. SLPAD using most frequent label, called SLPAD-Frequent, outperforms SLPAD using random label, called SLPAD-Random, on the Call-SMS network. Figure 2 shows that SLPAD-Frequent outperforms SLPAD-Random on modularity over almost all timestamps of the Call-SMS network. We also ran this same test on the Friends and Family-SMS network, producing very similar results to the Call-SMS network. Each version of SLPAD was average over twenty runs, due to the randomness of the SLPAD algorithm. Because of these results, both SLPA and SLPAD will be assumed to use the frequent label feature for the rest of the section.
SLPAD performs comparably and faster than SLPA, LabelRankT, and DSCAN-O. On the physics network, represented by Figure 3 and Figure 4, SLPAD without community repair performs just below SLPA in modularity, but with a lower runtime. When community repair was added to SLAPD, it remained faster than SLPA, as well as boosted results far above regular SLPAD and above SLPA. DSCAN-O’s runtime matches SLPAD’s runtime in the first half of the timestamp, but as the network increases in size, DSCAN’s runtime increase quicker than SLPAD’s runtime. SLPAD was able to run faster than any algorithm we tested. This is due to the complexity of SLPAD, which is no longer that of SLPA’s O(Tn), but instead comes down to the nodes of communities that saw edge changes. So SLPAD has a complexity of O(Tx) where x <= n. SLPAD and LabelRankT both have a fluctuating runtime curve in Figure 4, due to the efficiency of each algorithm to only update segments of the network where changes occurred; the amount of changes from one timestamp to another is the cause of the fluctuating runtimes. Note that tests on SLPAD were averaged over ten runs to account for the fluctuating results due to randomness of the algorithm. DSCAN-O suffers in modularity due to its detection of hubs and outliers, making modularity comparison inefficient to compare DSCAN-O to other algorithms.
Figure 5 and Figure 6 show the modularity and EQ of the community structures found by these same algorithms on the Call-SMS network. SLPAD produced similar modularity to SLPA and better than LabelRankT and DSCAN-O, as well as generating similar EQ to SLPA, and DSCAN-O. SLPAD with community repair did not improve SLPAD’s community structure as significantly on the Call-SMS network as it did on the Physics network, due to SLPAD not needing as much repair for this network. DSCAN-O is still hindered in both modularity and EQ because of detecting hubs and outliers, which decrease these two measures.
When comparing SLPAD and SLPA, we can also compare how they detect overlapping nodes. Figure 7 and Figure 8 show the similarity in overlapping nodes found by SLAPD and SLPA for each timestamp of the Physics network and the Call-SMS network respectively. We can see that SLPAD and SLPA are somewhat similar in overlapping node detection. It is important to note the beginning of both graphs; at first, both graphs are perfectly similar, which is caused by neither graph having found any overlapping nodes yet, and is followed by a sudden drop to zero, which occurs when one algorithm finds overlapping nodes while the other still has not. After these two irregularities, both algorithms start detecting overlapping nodes, and normal results are produced. Similarity is defined as:
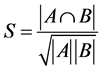
where A and B are the sets of overlapping nodes being compared by two algorithms on the same timestamp.
As noted before, SLPAD can be run as a threaded algorithm. Features of SLPAD that can run synchronously are: nodes can receive labels from its neighbors for one iterator at a time, removing low frequency labels from each node, and our community repair function. In view of large networks, performing these operations synchronously greatly increases overall runtime. Figure 9 shows the comparison between SLPAD being threaded and unthreaded, or SLPAD-Threaded and SLPAD-Unthreaded, runtimes for each timestamp on the physics network. As depicted, a low number of changes results in inefficiency from threading due to the memory overhead needed for threading, making SLPAD-Unthreaded ideal for small edge changes. For a large number of edge changes, SLPAD-Unthreaded’s runtime increases at a greater rate than SLPAD-Threaded. Figure 10 and Figure 11 show the number of edges changed and the number of nodes that will need to be updated for each timestamp. Node changes reflect all nodes of communities that saw edge changes and will be updated. As the number of edge and node changes increases, the runtime for SLPAD-Unthreaded increases while SLPAD-Threaded has a slower increase in runtime.
8. Conclusion
When discovering communities in dynamic networks, SLPAD performs faster than any other algorithm we tested and produces comparable, if not better, results in terms of modularity and EQ almost all the time. When running on the Call-SMS network, SLPAD produced about equal communities of similar modularity with both SLPA and LabelRankT. SLPAD was also able to produce better modularity with a shorter runtime than Labe-
Figure 2. Modularity of communities in the Call-SMS network found by SLPAD-Random and SLPAD-Frequent.
Figure 3. Runtime of each algorithm took to process the physics network. SLPAD takes less time than SLPA, LabelRankT, and DSCAN-O.
Figure 4. Modularity of communities in the physics network found by each algorithm.
Figure 5. Modularity of communities in the Call-SMS network found by each algorithm.
Figure 6. EQ of overlapping communities in the Call-SMS network found by each algorithm.
Figure 7. Similarity in overlapping nodes detected by SLPAD and SLPA in the physics network, with 1 representing exact similarity and 0 representing no similarity.
Figure 8. Similarity in overlapping nodes detected by SLPAD and SLPA in the Call-SMS network, with 1 representing exact similarity and 0 representing no similarity.
Figure 9. Runtime comparison between SLPAD-Threaded and SLPAD- Unthreaded.
Figure 10. Edge changes occuring in the physics network.
Figure 11. Node changes occuring in the physics network.
lRankT on the physics network. On both the physics and Call-SMS networks, SLPAD was also able to detect a mildly similar amount of overlapping nodes when compared to SLPA. SLPAD proves to be a fast and reliable dynamic community detection algorithm that is capable of producing communities of similar or better quality when compared to existing algorithms.
Acknowledgements
We would like to thank Houghton College for its financial support.
References
- Raghavan, U.N., Albert, R. and Kumara, S. (2007) Near Linear Time Algorithm to Detect Community Structures in Large-Scale Networks. Physical Review E, 76, Article ID: 036106. http://dx.doi.org/10.1103/PhysRevE.76.036106
- Xie, J.R., Szymanski, B.K. and Liu, X.M. (2011) Slpa: Uncovering Overlapping Communities in Social Networks via a Speaker-Listener Interaction Dynamic Process. 2011 IEEE 11th International Conference on Data Mining Workshops (ICDMW), Vancouver, 11-11 December 2011, 344-349.
- Xie, J.R. (2012) Agent-Based Dynamics Models for Opinion Spreading and Community Detection in Large-Scale Social Networks. Diss. Rensselaer Polytechnic Institute, Troy.
- Aston, N. and Hu, W. (2014) Community Detection in Dynamic Social Networks. Communications and Network 6.02, 124.
- Pizzuti, C. (2008) GA-Net: A Genetic Algorithm for Community Detection in Social Networks. Parallel Problem Solving from Nature—PPSN X. Springer, Berlin Heidelberg, 1081-1090.
- Leskovec, J., Kleinberg, J. and Faloutsos, C. (2005) Graphs over Time: Densification Laws, Shrinking Diameters and Possible Explanations. In: Proceedings of the Eleventh ACM SIGKDD International Conference on Knowledge Discovery in Data Mining, ACM, New York, 177-187.
- Hristova, D., Musolesi, M. and Mascolo, C. (2014) Keep Your Friends Close and Your Facebook Friends Closer: A Multiplex Network Approach to the Analysis of Offline and Online Social Ties. arXiv preprint arXiv:1403.8034
- Aharony, N., et al. (2010) Tracing Mobile Phone App Installations in the “Friends and Family” Study. Proceedings of the 2010 Workshop on Information in Networks (WIN’10).
- Newman, M.EJ. (2006) Modularity and Community Structure in Networks. Proceedings of the National Academy of Sciences, 103, 8577-8582. http://dx.doi.org/10.1073/pnas.0601602103
- Shen, H.W., et al. (2009) Detect Overlapping and Hierarchical Community Structure in Networks. Physica A: Statistical Mechanics and its Applications, 388, 1706-1712.












