Journal of Software Engineering and Applications
Vol.5 No.4(2012), Article ID:18573,7 pages DOI:10.4236/jsea.2012.54032
Comparative Study of the Performance of M5-Rules Algorithm with Different Algorithms
![]()
Department of Information Technology, Chandigarh Engineering College, Mohali, India.
Email: hitikaduggal@gmail.com, singh.parminder06@gmail.com
Received September 28th, 2011; revised February 5th, 2012; accepted March 1st, 2012
Keywords: Software Cost Estimation; Effort Estimation; Effort Estimation Models; Rule Generation; COCOMO Model; Conjunctive Rule Learner; Decision Table; M5-Rules Learner
ABSTRACT
The effort invested in a software project is probably one of the most important and most analyzed variables in recent years in the process of project management. The determination of the value of this variable when initiating software projects allows us to plan adequately any forthcoming activities. As far as estimation and prediction is concerned there is still a number of unsolved problems and errors. To obtain good results it is essential to take into consideration any previous projects. Estimating the effort with a high grade of reliability is a problem which has not yet been solved and even the project manager has to deal with it since the beginning. In this study, performance of M5-Rules Algorithm, single conjunctive rule learner and decision table majority classifier are experimented for modeling of Effort Estimation of Software Projects and performance of developed models is compared with the existing algorithms namely Halstead, Walston-Felix, Bailey-Basili, Doty in terms of MAE and RMSE. The proposed techniques are run in the WEKA environment for building the model structure for software effort and the formulae of existing models are calculated in the MATLAB environment. The performance evaluation criteria are based on MAE and RMSE. The result shows that the M5-Rules have the best performance and can be used for the effort estimation of all types of software projects.
1. Introduction
Software effort estimation is the critical part of software projects. Effective development of software is based on accurate effort estimation. Many quantitative software cost estimation models have been developed and implemented by practitioners in the past three decades. These include predictive parametric models such as Boehm’s COCOMO models [1], Price S [2] and analytical models such as those introduced in [3-5]. An empirical model uses data from previous projects to evaluate the current project and derives the basic formulae from analysis of the particular database available. An analytical model, on the other hand, uses formulae based on global assumptions, such as the rate at which developer solves problems and the number of problems available [6]. A good software cost estimate should be conceived and supported by the project manager and the development team. It is accepted by all stakeholders as realizable. It is based on a welldefined software cost model with a credible basis. It is based on a database of relevant project experience and it should be defined in enough detail so that its key risk areas are understood and the probability of success is objectively assessed [7].
In this paper, the performance of single conjunctive rule learner, M5-Rules Algorithm and decision table majority classifier is compared for Modeling of Effort Estimation of Software Projects. The dataset is based on the cost factors in COCOMO II. The performance of the developed model was tested on NASA software project dataset and compared to the models presented in [8-11]. The developed models were able to provide good estimation capabilities as compared to other models provided in the literature.
The remainder of this paper can be described as follows:
Section 2 outlines the literature review about the techniques that are used for effort and cost estimation. Section 3 discusses the methodology adopted for generating and comparing a number of models. Section 4 highlights results of implementation. It discusses the results of the various models used for the effort estimation and Section 5 is all about conclusions of this research work.
2. Related Work
One of the most important problems faced by software developers and users is the prediction of the size of a programming system and its development effort. Software effort estimation stands as the oldest and most mature aspect of software metrics towards rigorous software measurement. Considerable research had been carried out in the past, to come up with a variety of effort prediction models. The background information of various software effort and estimation models to be used in this research work is discussed as follows:
• M. H. Halstead [11] in 1977 proposed the model which predicts the rate of error and do not require the in-depth analysis of programming structure. It proposed the code length and volume metrics. Code length is used to measure the source code program and volume corresponds to the amount of required storage space. Numerous industry studies support the use of Halstead in predicting programming effort and mean number of programming bugs. However it depends on completed code and has little or no use as a predictive estimating model.
• Walston-Felix Model developed by C. E. Walston and C. P. Felix in 1977 at IBM provides the relationship between delivered lines of source code (L in thousands of lines) and effort E (E in person-month).
• Doty Model [12] published in 1977, is used to estimate efforts for Kilo lines of code (KLOC). This model constitutes various aspects of the software development environment such as user participation, customeroriented changes, memory constraints etc.
• Bailey and Basily [13] in 1981 described a meta-model which allows the development of effort estimation equations which are best adapted to a given development environment. The resultant estimation model will be similar to that of IBM and COCOMO is based on data collected by organization which captures its environmental factors and the differences among given projects.
• Albrecht has developed a methodology to estimate the amount of the “function” the software is to perform, in terms of the data it is to use (absorb) and to generate (produce). The “function” is quantified as “function points,” essentially, a weighted sum of the numbers of “inputs”, “outputs”, “master files”, “inquiries” provided to, or generated by, the software. Albrecht-Gaffney model established by IBM DP Services Organization, uses function point to estimate efforts.
Typical major models that are being used as benchmarks for software effort estimation are:
• Halstead
• Walston-Felix
• Doty (for KLOC > 9)
• Bailey-Basili All these models have been derived by studying large number of completed software projects from various organizations and applications to explore how project sizes mapped into project effort. But still these models are not able to predict the effort estimation accurately.
As the exact relationship between the attributes of the effort estimation is difficult to establish, so machine learning approaches could serve as an automatic tool to generate model by formulating the relationship based on its training. In this proposed study, it is tried to build a more accurate model that can provide accurate estimates of effort required to build a software system when compared with the other models provided in the literature.
Cost Estimation Model
COnstructive COst MOdel (COCOMO) [14,15] is used to estimate the software cost. It was first published in 1981 (COCOMO 81) and in 1997 (COCOMO II). Some differences between COCOMO 81 and COCOMO II are as follows: COCOMO 81 has 63 data points, uses Kilo Deliverable Source Instructions (KDSI) to measure the project size and three development modes to be represented by scale factors. In contrast, COCOMO II has 161 data points, uses KSLOC project size, and five scale factors.
The COCOMO software cost model measures effort in calendar months of 152 hours (and includes development and management hours). COCOMO assumes that the effort grows more than linearly on software size; i.e. months = a*KSLOC^b*c. Here, “a” and “b” are domainspecific parameters; “KSLOC” is estimated directly or computed from a function point analysis; and “c” is the product of over a dozen “effort multipliers” i.e. months = a*(KSLOC^b)*(EM1* EM2 * EM3 * ...). In COCOMO I, the exponent on KSLOC was a single value ranging from 1.05 to 1.2.
In COCOMO II, the exponent “b” was divided into a constant, plus the sum of five “scale factors” which modeled issues such as “have we built this kind of system before?”. The COCOMO I, effort multipliers are similar but COCOMO II dropped one of the effort multiplier parameters; renamed some others; and added a few more (for “required level of reuse”, “multiple-site development”, and “schedule pressure”). The effort multipliers fall into three groups: those that are positively correlated to more effort; those that are negatively correlated to more effort; and a third group containing just schedule information. In COCOMO I, “sced” have a U-shaped correlation to effort; i.e. giving programmers either too much or too little time to develop a system can be detrimental. The actual development effort is expressed in months (one month = 152 hours and includes development and management hours). The cost factors are shown in Table 1.
3. Used Methodology
The following steps are used for the comparative study:
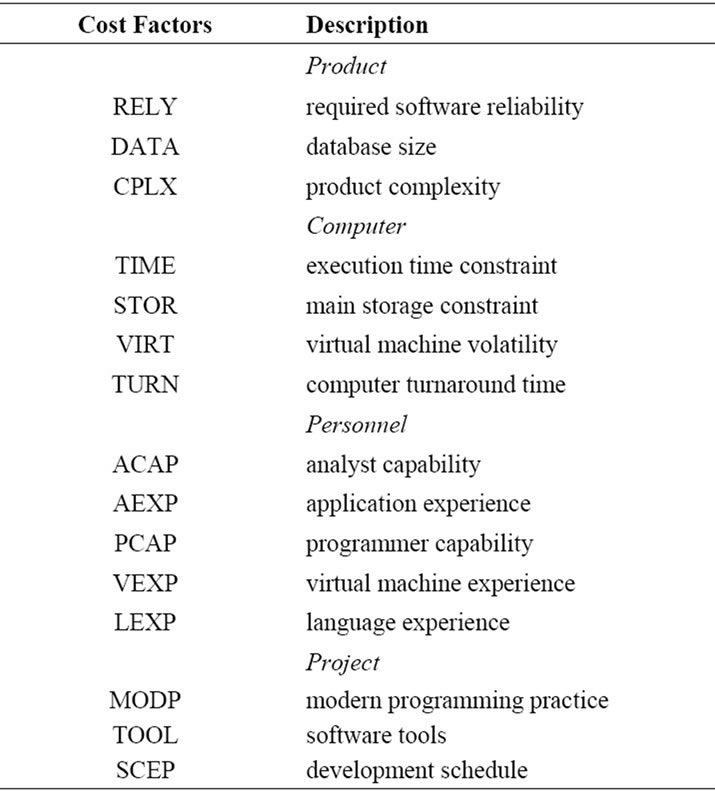
Table 1. Cost factors in COCOMO II.
3.1. Preliminary Study
First, Survey of the existing Models of Effort Estimation is to be performed.
3.2. Data Collection
Secondly, Historical Data being used by various existing models for the cost estimation is collected.
3.3. Effort Calculation Using Different Models
The following models are used for the data collected in the previous step and the effort for each developed approach is calculated.
• M5-Rules Algorithm
• Decision Table Majority Classifier
• Single Conjunctive Rule Learner
• Halstead Model
• Walston-Felix Model
• Bailey-Basili Model
• Doty Model In addition to single conjunctive rule learner, M5- Rules Algorithm and decision table majority classifier, the different existing models: Halstead Models, WalstonFelix Model, Bailey-Basili Model and Doty Model are also used for the comparison of results. The equations for the existing models are as under: (Table 2)
3.4. Performance Evaluation Criteria for Comparison of Models
The following performance criteria’s are adapted to ac-
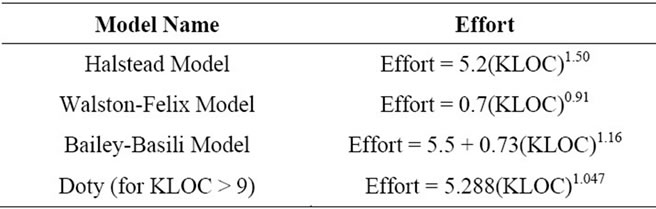
Table 2. Existing effort estimation models.
cess and evaluate the performance of effort estimation models.
Mean absolute error (MAE)

where actual output is a, expected output is c.
Mean absolute error, MAE, is the average of the difference between predicted and actual value in all test cases; it is the average prediction error [16].
Root Mean-Squared Error (RMSE)
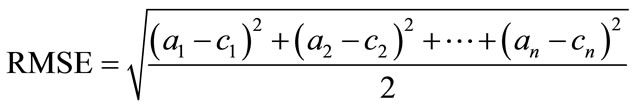
where actual output is a, expected output is c.
Root Mean Square Error, RMSE is frequently used measure of differences between values predicted by a model or estimator and the values actually observed from the thing being modeled or estimated [16]. It is just the square root of the mean square error.
The mean-squared error, MSE is one of the most commonly used measures of success for numeric prediction. This value is computed by taking the average of the squared differences between each computed value and its corresponding correct value.
The root mean-squared error is simply the square root of the mean-squared-error. The root mean-squared error gives the error value the same dimensionality as the actual and predicted values. The mean absolute error and root mean squared error is calculated for each machine learning algorithm.
4. Results & Discussion
The implementation of used methodology is done in WEKA open source software [17], and certain calculations are performed in the MATLAB environment. Different steps discussed in the methodology are implemented and the comparative analysis of various models is done in terms of MAE and RMSE values.
Table 3 shows the publicly available PROMISE Software Engineering Repository data set which is used for the experimentation. It consists of 93 instances each with 23 input attributes and one output attribute named as effort. Figures 1-3 describes the statistical analysis of different input attributes.
Table 3. COCOCMO NASA 2 data set.
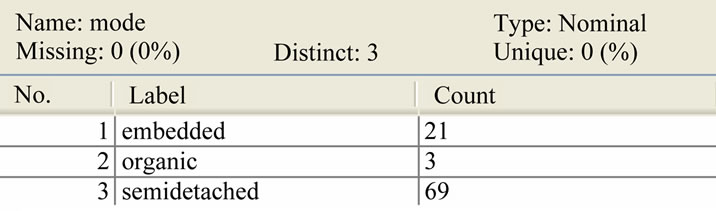
Figure 1. Statistical analysis of input attribute (mode) used in dataset.
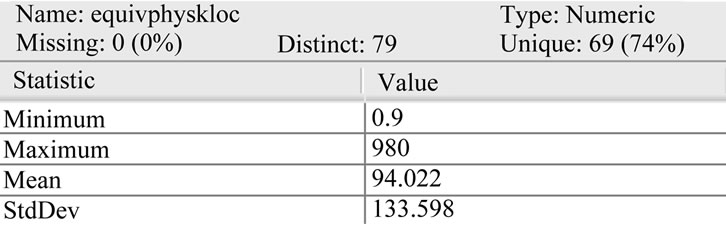
Figure 2. Statistical analysis of input attribute (equivphysloc) in dataset.
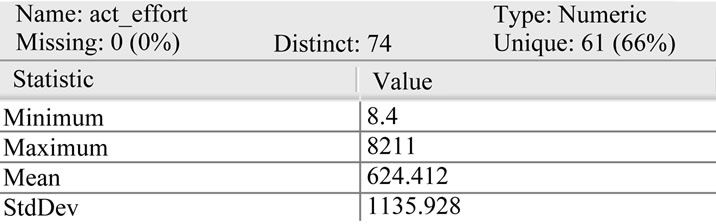
Figure 3. Statistical analysis of input attribute (act_effort) in dataset.
COCOMO attributes expressed in terms of classes {vl, l, n, h, vh, xh} is described in Figure 4.
Experimental Results of Machine Learning Algorithms
Historical COCOMO NASA 2/Software cost estimation dataset for the effort estimation is collected and used for

Figure 4. Effort multipliers of COCOMO II model.
the modeling in WEKA environment. The dataset consists of 93 NASA projects from different centers. The single conjunctive rule learner, M5-Rules Algorithm and decision table majority classifier are run in the WEKA environment and are evaluated by the cross validation using the 10 number of folds.
The Mean Absolute Error is taken as the average of the difference between predicted and actual value. Root Mean Square Error is taken as the measure of the differences between values predicted by a model and values actually observed from the thing being modeled. It is the average of the squared differences. The performance of the models is tested on the NASA software project data shown in Table 3.
Table 4 shows that the M5-Rules learner has the least MAE and RMSE value in comparison to Conjunctive Rule Learner and Decision table classifier. Hence the M5-Rules algorithm is the best methodology for classification as shown in Figure 5.
The 2d plot between the actual effort and the predicted actual effort shown in Figure 6 gives the classifier errors. It gives the result of classification. Crosses represent the correctly classified instances.
The existing effort estimation models namely Halstead Model, Waltson-Felix Model, Bailey-Basili Model, Doty (for KLOC > 9) are run in the MATLAB environment. Effort Estimation for these models are evaluated by using the formulas mentioned in the Table 2. The Historical COCOMO NASA 2 dataset is used for effort estimation by existing models. Table 5 describes the KLOC and actual effort pair used for the effort estimation. The KLOC is the Kilo lines of Code. E is effort in manmonths. The performance of the machine learning algorithms and existing algorithms measured in MAE and RMSE values is shown in Table 6. Figure 7 depicts the
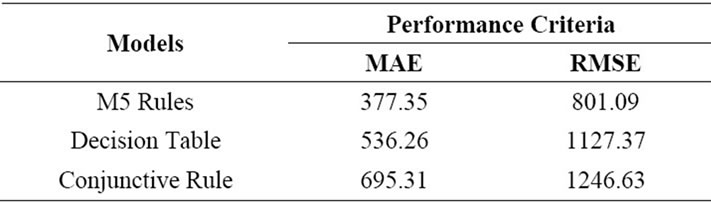
Table 4. Performance of machine learning algorithms
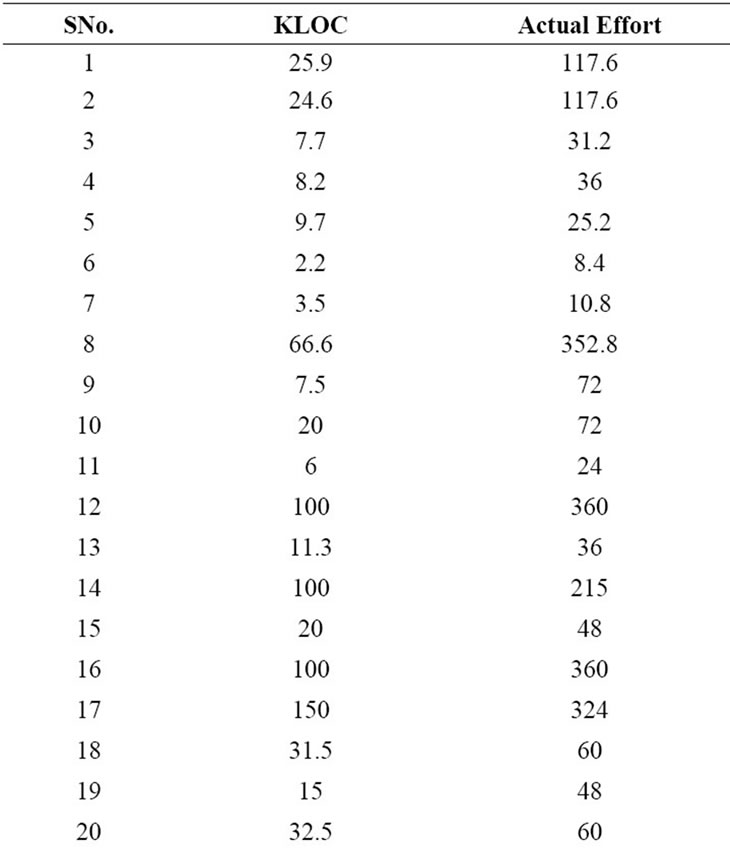
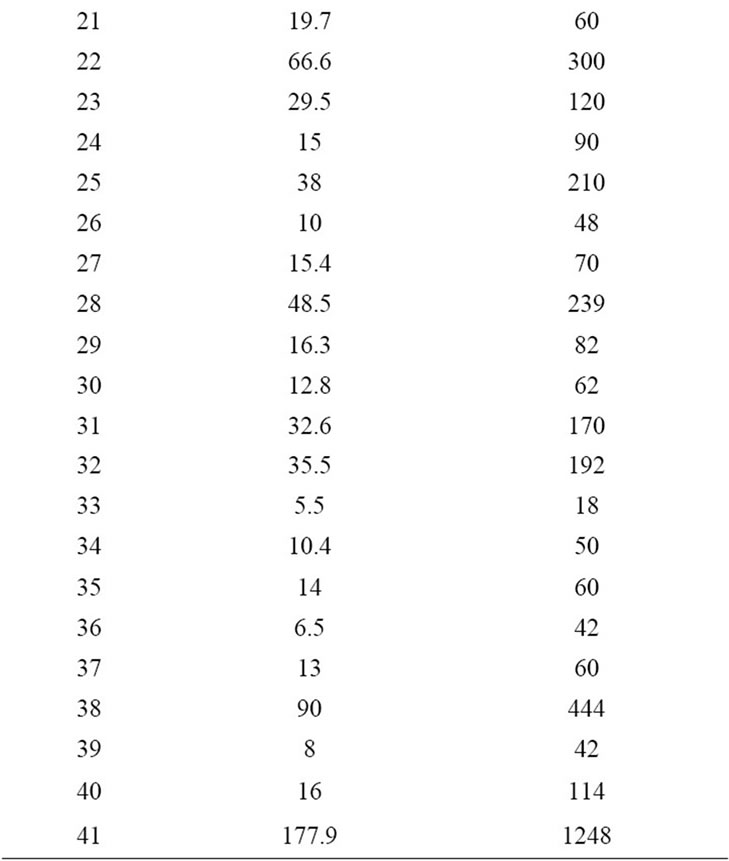

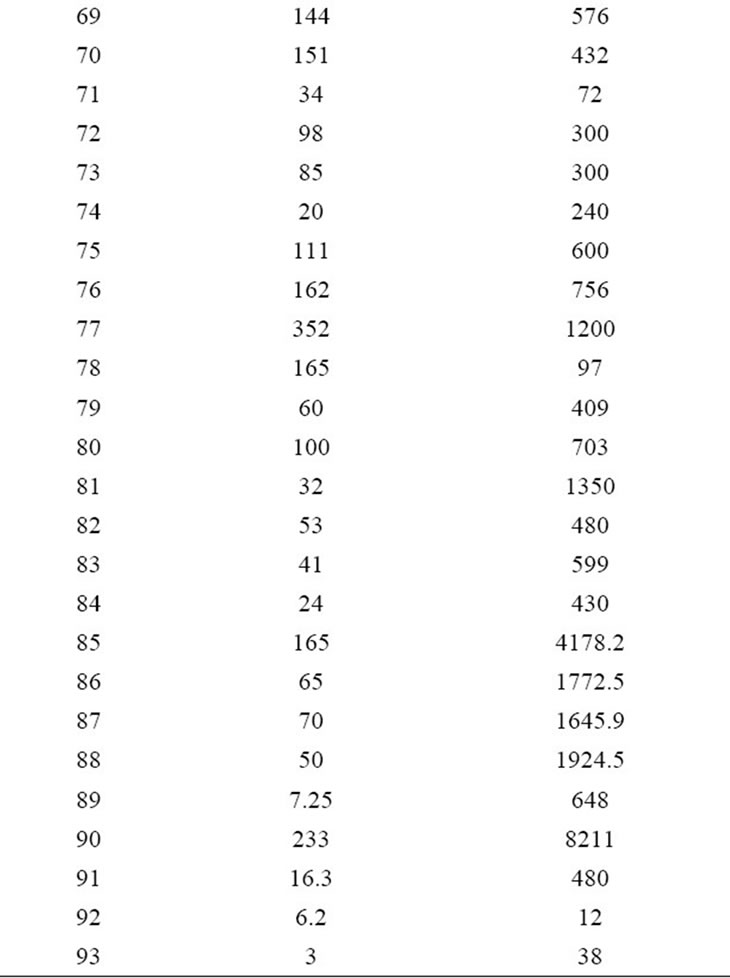
Table 5. KLOC and actual effort pair for effort estimation.
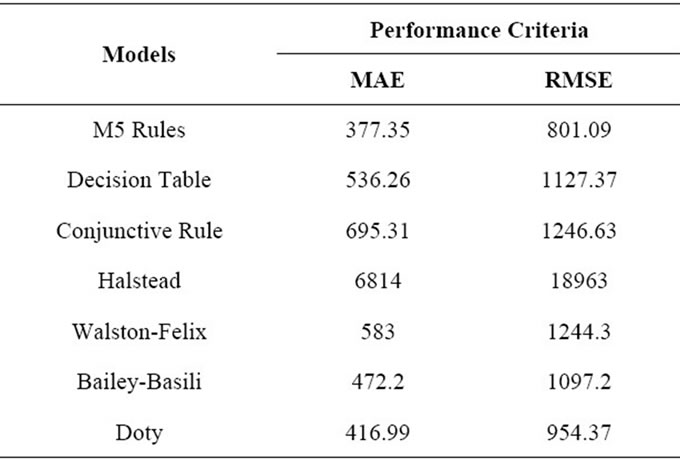
Table 6. Performance of machine learning algorithms along with other existing models.
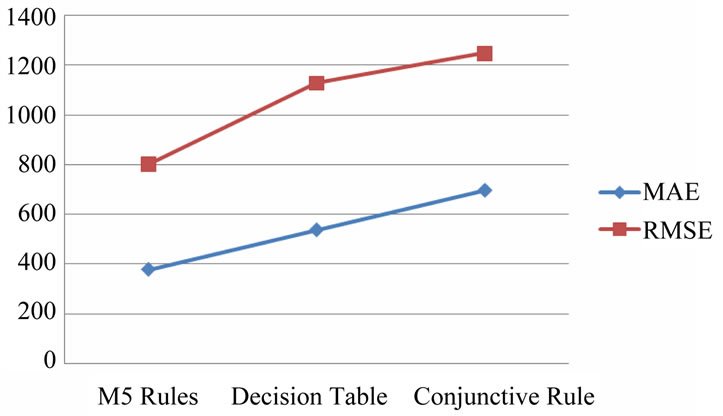
Figure 5. Comparison among machine learning models in terms of MAE and RMSE.
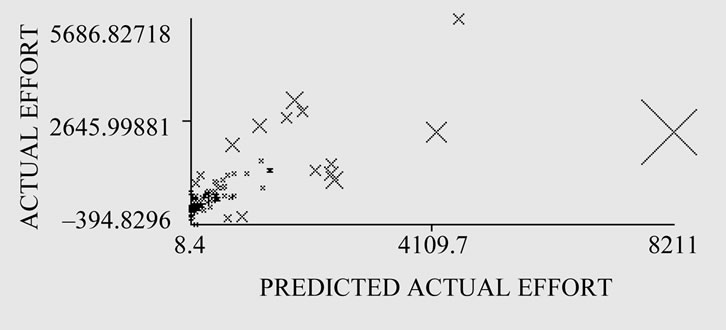
Figure 6. 2-d plot between the actual effort and the predicted actual effort for M5 rules learner.

Figure 7. Comparison among different models.
comparison in terms of mean absolute error and root mean square error for different models.
5. Conclusion
In this paper, various Machine learning Algorithms, Conjunctive Rule Learner, M5-Rules algorithm and Decision Table Majority Classifier are experimented to estimate the software effort for projects. Performances of these models are tested on NASA Software Project Data and the results are compared with the Halstead, WalstonFelix, Bailey Basili, Doty Models mentioned in the literature. The proposed M5 Rule learner shows best results than among other algorithms experimented in the study with lower values of MAE and RMSE calculated as 377.35 and 801.09 respectively and able to provide good estimation capabilities as compared to other models. Hence, it is suggested to use of M5-Rules technique to build suitable model structure for the software effort.
REFERENCES
- B. W. Boehm, “Software Engineering Economics,” 1st Edition, Prentice-Hall, Englewood Cliffs, 1981.
- S. Price, 2007. http://www.pricesystems.com
- G. Cantone, A. Cimitile and U. De Carlini, “A Comparison of Models for Software Cost Estimation and Management of Software Projects,” In: Computer Systems: Per- formance and Simulation, Elsevier Science, Amsterdam, 1986, pp. 123-140.
- L. H. Putnam, “A General Empirical Solution to the Macro Software Sizing and Estimating Problem,” IEEE Transactions on Software Engineering, Vol. SE-4, No. 4, 1978, pp. 345-361. doi:10.1109/TSE.1978.231521
- N. A. Parr, “An Alternative to the Raleigh Curve Model for Software Development Effort,” IEEE Transactions on Software Engineering, 1980, pp. 77-85.
- P. S. Sandhu, M. Prashar, P. Bassi and A. Bisht, “A Model for Estimation of Efforts in Development of Software Systems,” World Academy of Science, Engineering and Technology, Vol. 56, 2009.
- W. Royce, “Software Project Management: A Unified Framework,” Addison Wesley, Boston, 1998.
- B. W. Boehm, et al., “The COCOMO 2.0 Software Cost Estimation Model,” American Programmer, 1996, pp. 2- 17.
- C. E. Walston and C. P. Felix, “A Method of Programming Measurement and Estimation,” IBM Systems Journal, Vol. 16, No. 1, 1977, pp. 54-73. doi:10.1147/sj.161.0054
- J. Albrecht and J. E. Gaffney, “Software Function, Source Lines of Codes, and Development Effort Prediction: A Software Science Validation,” IEEE Transactions on Software Engineering, Vol. SE-9, No. 6, pp. 639-648. doi:10.1109/TSE.1983.235271
- M. H. Halstead, “Elements of Software Science,” Elsevier, New York, 1977.
- Doty Associates, Inc., “Software Cost Estimates Study,” Vol. 1, 1977, pp. 77-220.
- J. W. Bailey and V. R. Basili, “A Meta-Model for Soft Ware Development Resource Expenditures,” Proceedings of the 5th International Conference on Software Engineering, 1981, pp. 107-116.
- J. Baik, B. Boehm and B. Steece, “Disaggregating and Calibrating the CASE Tool Variable in COCOMO II,” IEEE Transactions on Software Engineering, Vol. 28, No. 11, 2002, pp. 1009-1022. doi:10.1109/TSE.2002.1049401
- S. Devnani-Chulani, B. Clark and B. Boehm, “Calibration Results of COCOMO II.1997,” 22nd Annual Software Engineering Workshop, NASA Goddard Space Flight Center, 1997.
- V. U. B. Challagulla, F. B. Bastani, I.-L. Yen and R. A. Paul, “Empirical Assessment of Machine Learning Based Software Defect Prediction Techniques,” 10th IEEE International Workshop on Object-Oriented Real-Time Dependable Systems, Sedona, 2-4 February 2005, pp. 263-270. doi:10.1109/WORDS.2005.32
- WEKA, 2007. http://www.cs.waikato.ac.nz/~ml/weka

