Journal of Service Science and Management
Vol.08 No.01(2015), Article ID:53746,10 pages
10.4236/jssm.2015.81006
Bayesian Conjoint Analysis in Water Park Pricing: A New Approach Taking Varying Part Worths for Attribute Levels into Account
Stephanie Löffler, Daniel Baier
Brandenburg University of Technology Cottbus-Senftenberg, Cottbus, Germany
Email: Stephanie.loeffler@tu-cottbus.de
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 January 2015; accepted 31 January 2015; published 3 February 2015
ABSTRACT
Nowadays, the application of conjoint analysis for measuring customers’ preferences for goods and services is wide-spread in marketing. A sample of customers is confronted with fictive offers and asked for evaluations. From these responses part worths for attribute levels of the offers are estimated and used to develop an optimal design and pricing for an offer. However, especially in tourism, it can be observed that attribute importance not only differs between customers but also varies over a single customer’s usage situations and her/his mood. In this paper, we propose a measurement approach that respects this variation. Part worths are stochastically modeled and estimated using Bayesian procedures. The approach is applied to design and price a water park.
Keywords:
Bayesian Conjoint Analysis, Choice-Based Conjoint, Water Park, Pricing

1. Introduction
Since the 1970s conjoint analysis has been intensively used by tourism managers to design and price competing multi-attributed goods or services. Maybe the best known early application was Marriot’s introduction of the new hotel chain “Courtyard by Marriot” in 1982 [1] : To support the hotel chain managers, 50 important hotel chain attributes and altogether 167 levels were selected during workshops. So, e.g., for the attribute “Building shape” the levels “L-shaped w/landscape” and “Outdoor courtyard” were specified, for the attribute “Pool type” the levels “No pool”, “Rectangular shape”, “Free form shape”, and “Indoor/outdoor”. After this, a sample of business and nonbusiness travelers was asked to evaluate fictive offers―characterized by these attributes and levels―with respect to their willingness to stay overnight. The responses were analyzed using regression-like procedures, the resulting part worths later formed the basis for market share prediction and for the development of design and pricing recommendations. In 1988, six years after this data collection and analysis, already 111 “Courtyard by Marriot” hotels had been opened according to these recommendations. The guest-tracking studies showed that the travelers were highly satisfied with the hotel chain’s design and pricing. Also, the market share of the chain was within four percentage points of the predicted market share [1] . From then on, Marriot as well as other researchers and managers used this successful methodology. The applications range, e.g., from modeling tourists’ selection of holiday resorts [2] - [5] over the design and pricing of package tours [6] - [8] to the design of travel brochures and other advertising material [9] .
So, nowadays, conjoint analysis is widespread in tourism and other application fields. Selka and Baier [9] describe 1899 commercial applications over the last ten years alone in Germany. In most cases design (59%) and pricing problems (88%) were in the focus (multiple assignments allowed). Most of the applications used choice- based conjoint analysis (94%) and web interviewing (74%). However, Selka and Baier [9] also found out that the average validity of these applications has deteriorated over time. Selka and Baier [10] ascribe this deterioration partly to the advancement of online data collection: Respondents perform their evaluation tasks in changing environments with many distraction possibilities and therefore are not able to give unambiguous answers. As one possible solution to this problem often [11] [12] the usage of Bayesian procedures has been proposed where the respondents’ part worths are modeled in a more flexible (stochastic) manner than in traditional conjoint analysis. In this paper, we discuss this proposition in more detail and apply it to simulated and to real data in tourism. In section 2 the approach is motivated and discussed, section 3 summarizes an application to simulated data, section 4 describes an application where a major German water park wants to rethink the pricing. The paper closes with conclusions and outlook.
2. Bayesian Conjoint Analysis: Data Collection, Data Analysis, and Market Share Prediction
For measuring customers’ preferences with respect to multi-attributed goods and services, conjoint analysis is well-known and wide-spread [13] [14] . All variants of conjoint analysis have in common, that a sample of respondents is confronted with fictive offers―described conjointly by attribute levels. From the evaluations of these fictive offers part worths for the attribute levels are estimated and used to predict choice decisions in different market scenarios. The conjoint analysis variants differ with respect to the data collection formats and estimation procedures. However, since many years [15] [10] , the choice-based variant CBC (abbreviation for choice-based conjoint analysis, see [16] [17] ) is the most popular one. This popularity holds for all application fields, also for tourism research [5] [7] [18] .
2.1. Traditional Estimation of the Respondents’ Part Worths Using CBC
CBC is also known under the name discrete choice [18] [19] and received its popularity due to the wide-spread CBC software system [20] . This software system―like other CBC systems―supports that a sample of 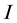 respondents
respondents 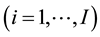 is subsequently confronted with
is subsequently confronted with 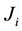 sets
sets 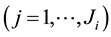 of
of 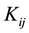 fictive offers
fictive offers 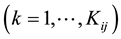 . The respondents are asked to select a most preferred fictive offer in each set. Let
. The respondents are asked to select a most preferred fictive offer in each set. Let 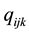 denote the results of these selections with
denote the results of these selections with 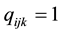 if
if  was the preferred fictive offer in set
was the preferred fictive offer in set 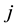 for respondent
for respondent  and
and  if not. The fictive offers and the sets of fictive offers are constructed in a balanced manner with respect to pre-defined attributes and levels. Typically, the levels of the attributes are nominal scaled with few values, but―for part worth estimation―are converted to interval scaled values using a dummy coding with respect to
if not. The fictive offers and the sets of fictive offers are constructed in a balanced manner with respect to pre-defined attributes and levels. Typically, the levels of the attributes are nominal scaled with few values, but―for part worth estimation―are converted to interval scaled values using a dummy coding with respect to 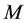 dimensions
dimensions 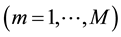 which indicate whether an offer has a specific level for each attribute (=1) or not (=0) leaving out one level per attribute as the reference level. So, e.g., let in the following, the
which indicate whether an offer has a specific level for each attribute (=1) or not (=0) leaving out one level per attribute as the reference level. So, e.g., let in the following, the 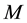 -dimensional vector
-dimensional vector 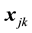 denote the dummy coded presence of
denote the dummy coded presence of 







as the probability that customer 







2.2. Estimation of an Empirical Distribution of the Respondents’ Part Worths
Bayesian procedures for conjoint analysis now differ from the above described modeling insofar that the model parameters 










The underlying idea for this modeling assumption is that the part worths of the respondents can vary over choices and that this variation has to be taken into account. So, e.g., when asked to evaluate a set of water park offers, a respondent can have different situations in mind, e.g., a short visit to go swimming alone or a day trip with the family. Depending on the situation in mind, the part worths for the attribute levels can vary. So, e.g., in the first situation the “low distance” has a higher and the “good quality” of the saunas and fun pools has a lower importance. The components allow modeling these different situations, the normal distribution allows to model unambiguous evaluations. The version with 

In order to estimate the model parameters 





• At the higher layer, we assume that respondents’ part worths 





• At the lower layer we assume that, given a respondent’s part worths 

The parameters are estimated by an iterative process where in each of these steps one set of parameters is re- estimated conditionally, given current values of the other sets, using Gibbs sampling. As a result we receive from each iteration a draw of all parameters. The draws across all iterations form joint empirical distributions of the model parameters. So, e.g., when 


The details of this iterative procedure generalize the estimation procedure given in Sawtooth Software [21] and are not given here (see Baier [22] for details in a similar setting), but it should be mentioned that Baier [22] has shown―in a similar setting for Bayesian procedures in metric conjoint analysis―that the version (with

2.3. Usage of the Empirical Distribution of the Respondents’ Part Worths for Design and Pricing
The empirical distribution of the respondents’ part worths can now be used also to predict choice probabilities of the respondents in an assumed market scenario with 



a similar formulation to (1) as the probability that respondent 

3. Application to Simulated Data
3.1. Generation of Empirical Part Worth Distributions
The first application is used to demonstrate the usefulness of the new approach. The simulated application domain is water park design and pricing. We assume that the competing offers can be described by 
Further, empirical part worth distributions for 
• segment 1 are “sport enthusiasts” (that usually go swimming but sometimes like also to visit a water park for relaxation),
• segment 2 are “families with children”,
• segment 3 are “working singles” (that like to swim in the morning but visit a water park on weekends),
• segment 4 are “retired persons” (with a small income that like to swim).
The chosen segments reflect the customer structure as reported by the management of the focused water park to create the most realistic result. For each segment two usage situations are assumed, one with a focus on “just swimming” and one with a focus on “a longer visit of a water parks. As discussed in the last section, we assume that the part worths across segments and usage situations may differ, so, the empirical distributions are generated by drawing values from mixtures of multivariate normal distributions with 

One can easily see that, e.g., all segments have in the usage situation “swim” a stronger focus on the attribute level “low distance” and that, e.g., the segment “family with children” has in the usage situation “visit” a stronger focus on “low price”. The weights reflect the proportions of the eight components across the sample, e.g., the segments “sports enthusiasts” and “family with children” are more important than “working singles” and “retired persons”. As additional distributional assumptions for the components a standard deviations of 1 was assumed. According to these settings, for each respondent an empirical distribution with 25 draws was generated. The results are shown in Figure 1. Additionally, in Figure 2, the mean part worths for the 20 persons are given. It should be mentioned that these averaged part worths in Figure 2 normally form the basis for the subsequent market simulation.
3.2. Market Simulation on Basis of the Empirical Part Worth Distributions and of the Means
The generated empirical part worth distributions are now used for market simulation. We assume a water park
Table 1. Mean part worths across segments and usage situations (8 components).
Figure 1. Empirical part worth distribution across all persons.
Figure 2. Mean part worths for all persons.
market scenario as described in Table 2. The table contains the actual 

Basing on the market prediction equation (3) sales predictions can be made for varying attribute levels “low price” and “high quality” with respect to the sample of respondents now.
Figure 3 reflects these predictions in percent of the status quo sales (with 
Table 2. Water park market scenario with four competing offers.
Figure 3. Sales depending on variations of the attribute levels “low price” and “high quality”.
4. Application to Real Data
Since the last years nearly 90 new water parks have been opened in Germany which offers bathing areas and wellness including saunas [24] . For a sustainable and successful competition in the leisure market, preferences should be measured especially in this branch in order to take appropriate measures for customer acquisition and customer retention. The regional water park of interest faces with this strong competition.
The main application tasks were to measure the customers’ preferences via a customer survey based on CBC and to predict market shares and sales under varying pricing and design options. In order to create realistic product profiles focus group interviews [14] were conducted with customers and water park managers. Additionally, an internet-based analysis of all regional water parks and a comparison of the services offered were made. But also, the attributes and levels were also selected in front of the background of former studies in tourism. So, e.g. Schroeder and Louviere [25] , Jurowski and Gursoy [26] , Moutinho [27] , and Nicolau and Más [28] discussed the importance of the attribute “low distance”, Milman [29] , Morley [30] , Nicolau [31] , Nicolau and Más [28] Pracejus and Olsen [32] Schroeder and Louviere [25] and Stevens [33] the attribute “low price”, Moutinho [27] , Thach and Axinn [34] and McClung [35] the attributes “fun pool” or “brine bath”, or Mueller and Kaufmann [36] the attribute “many saunas”. The corresponding levels were defined to reflect the status quo market scenario in the region but also to give hints for necessary improvements. So, e.g., for the “low price” attribute the levels “26 Euro” (dummy coded as “0”, for the day ticket) to “15 Euro” (dummy-coded as “1”) were specified. For the attribute “many saunas” the levels “5 Saunas” (dummy-coded as “0”) to “14 saunas” (as “1”) were selected.
For data collection, a CBC web interviewing approach was selected. The respondents were sampled using regional social networks and banners on websites were sports activities were promoted. A quota controlling was performed according to the water park management’s demands. So, e.g., the respondents were mainly sampled from residents of a near-by major town that forms the main customer reservoir for the water park. To fulfill the quota with respect to elderly people, also personal interviews were conducted. Each respondent had to deliver 16 choice tasks, each with three competing offers and an additional “none” alternative. Finally, a total of 201 interviews could be performed. Also, the respondent’s usage intensity of waterparks was collected to distinguish heavy from light users when predicting market shares. So, e.g., an adult that goes swimming one time a year got a weight of 1 whereas a family with two adults and more than one child that go swimming several times a weak received a weight of 300. The data collection took the different usage situations of the respondents into account by offering varying usage possibilities.
4.1. Part Worth Estimation
For part worth estimation, Sawtooth Software’s CBC/HB system was used that allows to derive for each respondent an empirical part worth distribution. The data validity was tested by using the averaged root likelihood value (RLH). This measure indicates how good the observed data are reproduced. A value of 1 indicates a perfect fit, a naïve model would result into a value of 1 divided by the number of alternatives in the choice sets. The collected data showed after calibration an averaged RLH Value of 0.613, which is clearly superior to 1/4―the value of a naïve model. Table 3 gives the resulting means of the empirical distribution of the part worths. One can easily see the high importance of the attribute “low price” but also―as in the simulated data application from above―the reduced information if we only take the mean part worths for each respondent.
Note that the estimated part worths are given in Table 3 just by their means and their standard deviations (one standard deviation with respect to all draws, one with respect to the means for each respondent). From the given means we can easily see that―on average―some of the attributes have a negative impact on the utility for a water parc (e.g. “Fun pool”), whereas most of the attributes have a positive impact (e.g. “Low distance”, “Low price” and so on). Also the “None” option also has a negative value (−5.719). This values can be interpreted as follows: In a market scenario with only one water park having level “1” for all attributes (except the “None” having a 0), the average utility for this water park would be 7.753, the average probability to select this water
park against the “None” option (having “0” at all attributes except “None”) would be
However, this would be a high quality offer at a very low price and would take into account that some respondents have higher “None” part worths and lower other part worths. Here, the usefulness of the introduced methodology can be easily seen: The empirical distribution of the draws across respondents and possible usage situations results in variation. It should be mentioned that the Bayesian procedures have the flexibility to model this inter- and intra-individual variations as discussed in the last section.
4.2. Market Simulation on Basis of the Empirical Part Worth Distributions and of the Means
Now, again as in the simulated application, we can predict market shares and sales in an assumed market scenario of competing water parks as defined in Table 4. Again, the table contains the actual 

Figure 4 gives the respective improvements in contrast to the actual sales. Again, there are some improvement possibilities (up to 113 %) and the results show that taking the means would lead to a suboptimal result.
Table 3. Means and standard deviations (SD) of the estimated empirical distribution of the part worths (“across all draws” and solely “across the means”).
Table 4. Waterpark market scenario with three competing and a “no choice” alternative.
Figure 4. Sales of water park 1 depending on variations of the attri- bute levels “low price” and “many saunas”
5. Conclusion and Outlook
The paper has presented a new approach to predict market shares in tourism on the basis of conjoint analysis. Instead of using the mean part worths for each respondent, the empirical distributions are used.
However some limitations of the study must be mention. The first point is the sample size. For a generalization more respondents needed. The second point is the chosen segments. Further analysis should use more differentiated or other customer segments to create more realistic results at all. The third point is the chosen attributes and attributes levels. Other researchers may use another set of attributes.
In conclusion it was demonstrated that the conjoint analysis proves to be a useful approach for pricing and design of water parks. The methodology has some advantages. The first is the use of the draws instead of mean part worths for each respondent. As presented the usual use of mean part worths lead to reduced information― therefore this technique is associated with a bias in the results. The second is the consideration of the combination of differentiated customer usage intensities and current family status whereby the customer value can be mirrored.
The results are promising, both in the simulated as well as the real data settings, but―of course―must be further analyzed.
References
- Wind, J., Green, P.E., Shifflet, D. and Scarbrough, M. (1989) Courtyard by Marriott: Designing a Hotel Facility with Consumer-Based Marketing Models. Interfaces, 19, 25-47. http://dx.doi.org/10.1287/inte.19.1.25
- Haider, W. and Ewing, G.O. (1990) A Model of Tourist Choices of Hypothetical Caribbean Destinations. Leisure Sciences, 12, 33-47. http://dx.doi.org/10.1080/01490409009513088
- Huybers, T. (2003) Domestic Tourism Destination Choices―A Choice Modelling Analysis. International Journal of Tourism Research, 5, 445-459. http://dx.doi.org/10.1002/jtr.450
- Kemperman, A., Borgers, A.W., Oppewal, H. and Timmermans, H.J. (2000) Consumer Choice of Theme Parks: A Conjoint Choice Model of Seasonality Effects and Variety Seeking Behavior. Leisure Sciences, 22, 1-18. http://dx.doi.org/10.1080/014904000272920
- Kemperman, A., Borgers, A.W., Oppewal, H. and Timmermans, H.J. (2003) Predicting the Duration of Theme Park Visitors’ Activities: An Ordered Logit Model Using Conjoint Choice Data. Journal of Travel Research, 41, 375-384. http://dx.doi.org/10.1177/0047287503041004006
- Chiam, M., Soutar, G. and Yeo, A. (2009) Online and Off-Line Travel Packages Preferences: A Conjoint Analysis. International Journal of Tourism Research, 11, 31-40. http://dx.doi.org/10.1002/jtr.679
- Dellart, B., Borgers, A. and Timmermans, H. (1995) A Day in the City: Using Conjoint Choice Experiments to Model Urban Tourists’ Choice of Activity Packages. Tourism Management, 16, 347-353. http://dx.doi.org/10.1016/0261-5177(95)00035-M
- Mazanec, J.A. (2002) Tourists’ Acceptance of Euro Pricing: Conjoint Measurement with Random Coefficients. Tourism Management, 23, 245-253. http://dx.doi.org/10.1016/S0261-5177(01)00086-3
- Huertas-Garcia, R., Laguna Garcia, M. and Consolation, C. (2012) Conjoint Analysis of Tourist Choice of Hotel Attributes Presented in Travel Agent Brochures. International Journal of Tourism Research, 16, 65-75. http://dx.doi.org/10.1002/jtr.1899
- Selka, S. and Baier, D. (2014). Kommerzielle Anwendung auswahlbasierter Verfahren der Conjointanalyse: Eine empirische Untersuchung zur Validitätsentwicklung. Marketing Zeitschrift für Forschung und Praxis, 1, 54-64.
- Baier, D. and Polasek, W. (2003) Market Simulation Using Bayesian Procedures in Conjoint Analysis. In: Schwaiger, M. and Opitz, O., Eds., Exploratory Data Analysis in Empirical Research, Springer, Berlin, 413-421. http://dx.doi.org/10.1007/978-3-642-55721-7_42
- Baier, D. and Gaul, W. (2007) Market Simulation Using a Probabilistic Ideal Vector Model for Conjoint Data. In: Gustafsson, A., Herrmann, A. and Huber, F., Eds., Conjoint Measurement: Methods and Applications, Springer, Berlin, 97-120. http://dx.doi.org/10.1007/978-3-540-71404-0_3
- Green, P.E., Krieger, A.M. and Wind, Y. (2001) Thirty Years of Conjoint Analysis: Reflections and Prospects. Interfaces, 31, 56-73. http://dx.doi.org/10.1287/inte.31.3s.56.9676
- Green, P.E. and Srinivasan, V. (1978) Conjoint Analysis in Consumer Research: Issues and Outlook. Journal of Consumer Research, 5, 103-123. http://dx.doi.org/10.1086/208721
- Sawtooth Software (2013) Results of 2013 Sawtooth Software User Survey. http://www.sawtoothsoftware.com/about-us/news-and-events/sawtooth-solutions/ss35-cb
- Desarbo, W.S., Ramaswamy, V. and Cohen, S.H. (1995) Market Segmentation with Choice-Based Conjoint Analysis. Marketing Letters, 6, 137-147. http://dx.doi.org/10.1007/BF00994929
- Louviere, J.J. and Woodworth, G. (1983) Design and Analysis of Simulated Consumer Choice or Allocation Experiments: An Approach Based on Aggregate Data. Journal of Marketing Research, 20, 350-367. http://dx.doi.org/10.2307/3151440
- Ben-Akiva, M. and Lerman, S.R. (1985) Discrete Choice Analysis: Theory and Application to Travel Demand. MIT Press, Cambridge.
- Ben-Akiva, M., Mcfadden, D., Abe, M., Böckenholt, U., Bolduc, D. and Gopinath, D. (1997) Modelling Methods for Discrete Choice Analysis. Marketing Letter, 8, 273-286. http://dx.doi.org/10.1023/A:1007956429024
- Sawtooth Software (2013) The CBC System for Choice-Based Conjoint Analysis. Version 8, Sawtooth Software. http://www.sawtoothsoftware.com/download/techpap/cbctech.pdf
- Sawtooth Software (2013) The CBC/HB System for Hierarchical Bayes Estimation. Version 5.0, Technical Paper. http://www.sawtoothsoftware.com/download/techpap/hbtech.pdf
- Baier, D. (2014) Bayesian Methods for Conjoint Analysis-Based Predictions: Do We Still Need Latent Classes? Studies in Classification, Data Analysis, and Knowledge Organization, 103-113. http://dx.doi.org/10.1007/978-3-319-01264-3_9
- Otter, T., Tüchler, R. and Frühwirth-Schnatter, S. (2004) Capturing Consumer Heterogeneity in Metric Conjoint Analysis Using Bayesian Mixture Models. International Journal of Research in Marketing, 21, 285-297. http://dx.doi.org/10.1016/j.ijresmar.2003.11.002
- European Waterpark Association (2014) Waterparks in Germany. http://www.freizeitbad.de/en/waterparks/waterparks-overview/germany.html
- Schroeder, H.W. and Louviere, J. (1999) Stated Choice Models for Predicting the Impact of User Fees at Public Recreation Sites. Journal of Leisure Research, 31, 300-324.
- Jurowski, C. and Gursoy, D. (2004) Distance Effects on Residents’ Attitudes toward Tourism. Annals of Tourism Research, 31, 296-312. http://dx.doi.org/10.1016/j.annals.2003.12.005
- Moutinho, L. (1988) Amusement Park Visitor Behavior―Scottish Attitudes. Tourism Management, 9, 291-300. http://dx.doi.org/10.1016/0261-5177(88)90003-9
- Nicolau, J.L. and Mas, F.J. (2006) The Influence of Distance and Prices on the Choice of Tourist Destinations: The Moderating Role of Motivations. Tourism Management, 27, 982-996. http://dx.doi.org/10.1016/j.tourman.2005.09.009
- Milmann, A. (2001) The Future of the Theme Park and Attraction Industry: A Management Perspective. Journal of Travel Research, 40, 139-147. http://dx.doi.org/10.1177/004728750104000204
- Morley, C.L. (1994) Discrete Choice Analysis of the Impact of Tourism Prices. Journal of Travel Research, 33, 8-14. http://dx.doi.org/10.1177/004728759403300202
- Nicolau, J.L. (2008) Characterizing Tourist Sensitivity to Distance. Journal of Travel Research, 47, 43-52. http://dx.doi.org/10.1177/0047287507312414
- Pracejus, J.W. and Olsen, G.D. (2004) The Role of Brand/Cause Fit in the Effectiveness of Cause-Related Marketing Campaigns. Journal of Business Research, 57, 635-640. http://dx.doi.org/10.1016/S0148-2963(02)00306-5
- Stevens, B.F. (1992) Price Value Perceptions of Travelers. Journal of Travel Research, 31, 44-48. http://dx.doi.org/10.1177/004728759203100208
- Thach, S.V. and Axinn, C.N. (1994) Patron Assessments of Amusement Park Attributes. Journal of Travel Research, 32, 51-60. http://dx.doi.org/10.1177/004728759403200308
- Mcclung, G.W. (1991) Theme Park Selection: Factors Influencing Attendance. Tourism Management, 12, 132-140. http://dx.doi.org/10.1016/0261-5177(91)90068-5
- Mueller, H. and Kaufmann, E.L. (2001) Wellness Tourism: Market Analysis of a Special Health Tourism Segment and Implications for the Hotel Industry. Journal of Vacation Marketing, 7, 5-17. http://dx.doi.org/10.1177/135676670100700101








