Journal of Biomedical Science and Engineering
Vol.10 No.05(2017), Article ID:76400,14 pages
10.4236/jbise.2017.105021
Comparison of Mathematical Equations Applicable to Tolerance of Total Body Irradiation in Humans and Decay of Isotopes, Uranium and Thorium: Differences and Similarity
Sung Jang Chung
Morristown-Hamblen Healthcare System, Morristown, TN, USA

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 2, 2017; Accepted: May 21, 2017; Published: May 24, 2017
ABSTRACT
A clear and exact quantitative relationship between dose of total body irradiation and mortality in humans is still not known because of lack of human data that would enable us to determine LD50 for humans in total body irradiation. Analysis of human data has been primarily from radiation accidents, radiotherapy and the atomic bomb victims. The author published the general mathematical equations of LD50 constructed on the basis of data presented by Cerveny, MacVittie and Young, employing the probacent formula model. In this study, the author compared the equations of tolerance of total body irradiation and decay of isotopes, uranium and thorium. Differences and similarity in these equations of the two groups are presented. The significance of similarity is specially described.
Keywords:
Total Body Irradiation; Formula of LD50, Decay of Isotopes, Half-Life of Isotopes, Safety in Radiotherapy and Space Flight, Probacent Model, Ultron-Logotron Theory, Theory of Everything

1. Introduction
A clear and exact quantitative relationship between dose of total body irradiation and mortality in humans is still not known because of lack of human data that would enable us to determine LD50 for humans in total body irradiation. Analysis of human data has been primarily from radiation accidents, radiotherapy and the atomic bomb victims [1] - [9] .
The author published a mathematical equation of LD50 constructed on the basis of the data published by Cerveny, MacVittie and Young [1] .
In decay of isotopes, an empirically constructed law is currently used to estimate their physical changes [10] [11] . It seems to the author that there are no articles in the literatures that compare the equations of total body irradiation in humans and decay of isotopes such as LD50 in humans and half-life in isotopes [10] [11] . In this study, the author compared these equations for humans and isotopes, uranium and thorium, and attempted to clarify differences and similarity in the equations of both groups.
1.1. General Mathematical Formula of the Probacent-Probability Equation in Biological Phenomena
The author published a general mathematical formula, Equation (1) that calculates probabilities of mortality or survival as a function of intensity of stimulus and duration of exposure in humans and other living organisms exposed to hazardous environments or noxious agents, overcoming the risk in biological phenomena [12] [13] [14] [15] [16] .
 (1a)
(1a)
 (1b)
(1b)
where i is intensity of stimulus, external stressor or noxious agent; t is duration of exposure; a, b, c, d and n are constants. P is ‘probacent’ (abbreviation of percent probability), a relative amount of internal stress caused by an external stressor or a relative amount of loss of reserve for survival. Probacent values of 0, 50 and 100 correspond to (mean-5 SD), mean and (mean + 5 SD), respectively; the unit of ‘probacent’ is 0.1 SD. In addition, 0, 50 and 100 probacents seem to correspond to 0, 50 and 100 percent probability, respectively in mathematical prediction problems in terms of percentage. Q is mortality probability (%). Survival probability (%) is (100 ? Q). Equation (1) can be used for survival probability problems.
An actual example of the relationship between the external stressor and the internal stress is the case of carbon monoxide poisoning in humans [17] . P values in the formula, Equations (2) and (3) express the carboxyhemoglobin levels in blood (the amount of internal stress) caused by inspired carbon monoxide in air (the external stressor) at rest (Equation (2)) and at light work(Equation (3)), respectively.
 (2)
(2)
 (3)
(3)
where C is concentration of CO in air (%) and t is duration of exposure (minute).
Equation (1) is fundamentally based on Gaussian normal distribution.
Equation (4) represents a general formula that expresses the probability of survival and mortality of US adult population, 2001 [14] [15] [18] . Data on the survival, mortality and life expectancy reported by the National Center for Health Statistics [19] are used to construct the equations.
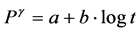 (4a)
(4a)
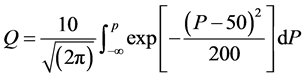 (4b)
(4b)
where P is probacent; t is age; Q is mortality (%); a, b and γ are constants. Survival probability (%),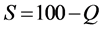 . The above distribution of Gaussian normal distribution becomes Weibull distribution if γ value = 1.
. The above distribution of Gaussian normal distribution becomes Weibull distribution if γ value = 1.
In general, as the first step of calculation in order to determine the constants, a, b and γ in Equation (4a), P-values are obtained from experimental data or clinical data, consulting the table of conversion of percent probability into probacent (see the author’s previous publications [12] [13] [16] ), then the constants can be determined with insertion of P-values into Equation (4a).
As the second step of calculation to obtain Q-values, a computer program of nonintegral calculation (Equation (6)) written by the author [13] [18] is used because the computer cannot perform integral. The program is written on the basis of an approximation equation, Equation 6 for a specific integral equation, Equation (5) [19] .
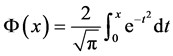 (5)
(5)
The digital computer used the following equation as an approximation for 0 ≤ X<∞.
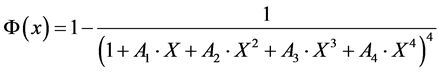 (6)
(6)
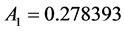
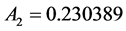
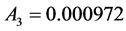
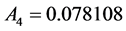
Mathematical transformation of Equation (4b) to Equation (6) is described in the author’s previous publication [13] and its detail is presented in the author’s book [20] .
Equation (7) of death rate D is derivable from Equation (4a) (see the author’s previous publication [14] [16] and Appendix of the current article).
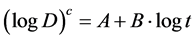 (7)
(7)
where D is death rate, t is age; A, B and c are constants.
Formulas of death rate (D) for US older adults are expressed by Equations (8) and (9).
Age group of 60 - 85 years:
 (8)
(8)
Age group of 85 - 100 years:
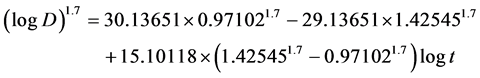 (9)
(9)
The probacent formula model has been applied to data in the biomedical literature; to express a relationship among plasma acetaminophen concentration, time after ingestion and occurrence of hepatotoxicity in man [21] ; to express survival probability in patients with heart transplantation [22] ; to express survival probability in patients with malignant melanoma [23] and to express relationship among age, height and weight, and percentile in Saudi and US children of ages 6 - 16 years [24] .
Mehta and Joshi [25] successfully applied the probacent-probability equation model to use model-derived data as an input for radiation risk evaluation of Indian adult population in their studies.
2.2. Equations of Tolerance of Total Body Irradiation in Humans
To my knowledge, there seem to be no general mathematical models in the literature that express the quantitative relationship among dose rate of radiation, duration of exposure and mortality and/or LD50 of lethal dose for humans in ionizing total body irradiation.
Data on LD5, LD10, LD50, LD90 and LD95 versus dose rate shown in a table of animal-model predictions of lethal radiation doses to humans published by Cerveny, MacVittie and Young [1] are used to construct predictive formulas. A general formula Equation (10) to express the relationship among dose rate, duration of exposure and mortality in humans exposed to total body irradiation is constructed, employing the general probcent model, Equation (4a) where the constant γ = 1 in Equation (10).
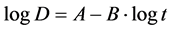 (10)
(10)
where D is dose rate (rad/min); t is duration of exposure (min); A and B are constants.
Equations (11)-(15) express relationships among dose rate in rad/min, duration of exposure in minutes and mortality probability in percentage, employing Equation (10) [26] [27] .
Various lethal dose values, LD5, LD10, LD50, LD90 and LD95in ionizing total body irradiation in humans can be calculated from these equations.
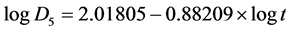 (11)
(11)




where D is dose rate (rad/min) and t is duration of exposure (minute).
If the duration of exposure, time t is given or at any given time t, then the dose rate D50 and lethal dose LD50 (a product of D50 x t) can be expressed by Equations (16) and (17), respectively.


Table 1 and Figure 1 illustrate the results and reveal a close agreement between formula-derived and animal-model-predicted data on lethal radiation doses, LD5-95 for humans in the total body irradiation (p > 0.995 in χ² test). The lines representing Equations (11)-(15) in Figure 1 are straight lines with different slopes.
There is a remarkable agreement between formula-predicted and published estimated LD50 and mortality probabilities [26] .
The t values in Equations (13), (16) and (17) seem to mathematically correspond to the half-life of isotopes in decay. The half-life t1/2 (=T1/2) (the duration of
Figure 1. Relationship among dose rate of radiation, duration of exposure and lethal radiation dose (LD5-95) in total body irradiation in humans. The abscissa represents duration of exposure in minutes (log scale). The ordinate represents dose rate in rad/min (log scale). Data points indicate lethal doses of LD5-95 and appear to fall on the five formula- predicted straight lines in each group, respectively (see text).
Table 1. Comparison of formula-derived and animal-model-predicted lethal radiation doses to humans.
Formula-derived lethal radiation doses are calculated from Equations (11)-(15), obtaining total dose (rad) by dose rate (rad/minute) D multiplied by duration of exposure, time t (minute). p > 0.995 in χ² test.
exposure for 50% survival, 50% life expectancy) can be expressed by Equation (18) and (19).


The formulas of the above equations, LD50 and mortality probability in lethal radiation exposure for humans might be helpful in preventing radiation hazard and injury, and further for safety in radiotherapy.
2.3. Equations of Decay in Radioisotopes, Uranium and Thorium
All radioactive decay in any isotopes follow the experimental law expressed by Equation (20) [10] [28] .

where N0 is the number of radioisotope atoms which have not decayed at present. N is the number of remaining atoms after time t. Consequently, the rate of decay each second is proportional to the number present and expressed by Equation (21).

The constant λ represents the probability that any given nucleus will decay in any given unit interval of time. λ is independent of the age of the nucleus of radioisotopes. λ values of uranium and thorium are 0.154 ´ 109 years and 0.049 ´ 109 years, respectively.
The half-life, T1/2, of any radioisotopes is given by Equation (22).

The half-life T1/2 of uranium-238 and thorium-232 is 4.5 billion years and 14.1 billion years, respectively.
Equation (23) expresses a relationship between half-life and energy of emitted alpha particle from isotopes.

where E is the energy of emitted alpha particle, A (slope) and B (intercept) are constants. Equation (24) is the equation for thorium-232 [10] . If empirical data on half-life T1/2 against E-1/2( in terms of E) of uranium or thorium are plotted on a log-log scale graph paper, each data of the two groups show a straight line, respectively [10] [11] [29] .

2. Differences in Equations of Total Body Irradiation in Humans and Decay in Isotopes
General equations of tolerance of total body irradiation in humans (A group) and decay of isotopes, uranium and thorium (B group) are compared as follows:
1. Mortality
Mortality in humans:


Decay in isotopes:

2. Survival probability (S):
Survival probability in humans:


Remaining probability after Decay in isotopes:

3. Death rate
Death rate in humans:

Decay rate:

The above comparison indicates clear differences in the equations of both groups, (A) and (B). The differences are considered to be due to the differences between non-uniformity vs uniformity in their structural organizations and sensitivities against the external stressor and/or internal stress of both groups under observations. Structural organizations of human bodies are complex and their sensitivities under observations are non-uniform. In contrast, the structural organization of radioisotope atoms is considered to be uniform and their sensitivity (response) against yet unknown internal stress or external stressor is uniform.
If LD5, LD10, LD50, LD90 and LD95 against time (duration of exposure) are plotted on a log-log scale graph paper, those data reveal multiple straight lines (Figure 1). In contrary, the data on isotopes, uranium-238 and thrium-232 reveal a single straight line, respectively [10] [11] .
3. Similarity in Equations of Tolerance of Total Body Irradiation in Humans and Decay in Isotopes
The energy of the emitted alpha particle can be deduced by using Einstein’s formula (E = mc2).

where mp is the mass of the parent nucleus, md is the mass of the daughter nucleus, and ma is the mass of the alpha particle (which is the He2 nucleus).


The relationship between dose rate D and duration of exposure t in total body irradiation in humans is expressed by Equation 26 [26] .

The relationship between dose rate and half-life (50% life expectancy for 50% survival probability) is expressed by Equation (27).

The half-life (the duration of exposure for 50% survival, 50% life expectancy) is inversely proportional to the dose rate.
Equation (28) expresses the relationship between the half-life of isotopes and the energy of emitted alpha particle.



If logT1/2 versus logE in Equation (30) instead of Equation (29) are plotted on a log-log graph paper, the data points reveal virtually a straight line [10] [11] as shown in Figure 1 that illustrates a similar straight line representing the data points of logT1/2 versus logD50. Consequently, Equation (27) for mortality in humans and Equation (30) for decay in isotopes reveal a similarity in their forms as well as in the straight lines in their graphic plottings. Both equations, Equations (27) and Equation (30) indicate a similar form. This result may indicate that the equation of decay of isotopes in quantum physics is derivable from the equation of mortality of total body irradiation in humans. The internal stress amount caused by the external stressor, total body irradiation reflects the dose rate. The energy of the emitted alpha particle reflects the internal stress amount in isotope atoms. The internal stress amount is thus common in both phenomena and seems to make the similarity in the forms of Equations (27) and (30).
The internal stress (energy) is proportional to the dose rate D50 , and the internal stress of the isotope atom is reflected in the energy E of the emitted alpha particle. On the basis of the similarity in both Equations (27) and (30) and the straight line in both graphic plotting of both equations, Equation (27A) is assumed to express the above relation.



Equation (27C), (27) and (30) reveal a remarkable similar mathematical form.
The general formulas of the probacent-probability equation are experimentally (experimental data with animals) [12] [30] [31] [32] and/or empirically (clinical data) constructed by the author and his coworkers [12] [13] [14] [15] [16] . Equations related to decay of isotopes are primarily empirically constructed [10] [11] .
The probacent model is applicable to express the relationship between dose rate and survival time in mice exposed to total body irradiation (p-value> 0.995 in χ² test) [33] . The probacent model was applied to the data on low dose rate versus cancer mortality risk, published by the United Nations (UNSCEAR, 2010) and other investigators, to construct general formulas expressing a relationship between dose and solid cancer or leukemia mortality probability after exposure to acute low dose ionizing radiation in humans. There is a remarkable agreement between formula-derived and published values of low dose and solid cancer or leukemia mortality probability (P > 0.997) [34] .
The probacent formula may provide a mathematical bridge connecting biology and quantum physics. The probacent formula gave a special momentum to the author to develop the hypothesis of the ultron-logotron theory related to mind and matter, consciousness and quantum physics (Theory of Everything), and further the possible deeper structure of leptons and quarks on the basis of quantum physics and Confucian philosophy [35] [36] [37] .
It has been recently discovered that electrons split into two separate parts: a spinon (a neutral magnet behaving as a tiny compass needle) and an orbiton carrying its electron motion (negative electrical charge) around the nucleus [38] [39] [40] . The spinon and orbiton seem to correspond to the neutral part of yin- and yang-ultrons composite and the negative part of yin-ultron as predicted in the ultron-logotron theory, respectively [37] . Yin- and yang-ultrons in a spinon are postulated to line up in a tiny series magnet arrangement with a south and a north pole in one direction that can generate spin. This substructure of electron suggests that a quark in a proton is likewise composed of two separable particles, a magnetic (of yin-and yang-ultrons composite) and an electrical particle (of yin- or yang-ultrons) [37] [44] [45] .
Hematopoietic cells of bone marrow, the intestinal tract, and the central nervous system are most vulnerable to radiation effects [5] [8] [41] . Death is caused by multi-organ failure. In case of relatively high doses, infection and hemorrhage are earliest contributing factors to death, resulting from the damage to the most sensitive hematopoietic cells in total body irradiation [1] [42] .
It has been recently proven in neuroscience that radiation caused pathologic cell changes in neurons of brain [43] . The hazard of total body irradiation to astronauts in a possible future long space flight to the mars or other stars would be very significant and serious so that the problems regarding safety of astronauts should be investigated [43] .
Further research would be needed for verification of the author’s formulas related to tolerance of total body irradiation in humans.
4. Conclusions
In this study, the mathematical equations applicable to tolerance of total body irradiation in humans and decay in isotopes, uranium and thorium are compared. The following differences and similarity as well as the significance in the equations of both groups are presented. A general formula of the probacent- probability equation is experimentally and empirically constructed and applicable as an approximation method to calculate probabilities of survival, mortality and death rate in humans and animals exposed to hazardous environments or noxious agents, overcoming the risk.
(1) Differences are present between the equations of tolerance of total body irradiation and decay of isotopes due to differences in uniformity of subjects under observations.
(2) There is a remarkable similarity between the forms of the equations of LD50 of total body irradiation in humans and half-life of isotopes.
(3) The equation of decay of isotopes seems to be derivable from the equation of dose rate of total body irradiation in humans.
(4) The mathematical probacent model may provide a mathematical bridge connecting biology and quantum physics.
(5) The equation of tolerance of total body irradiation in humans would be hopefully helpful in radiotherapy and in case of astronauts in a possible future long space flight in estimating their safety.
(6) Electrons split into two particles, a neutral particle (spinon) and a particle with a negative electrical charge (orbiton) [38] [39] [40] as predicted in the author’s ultron-logotron theory. This substructure of electron suggests that a quark is likewise composed of two separable particles, a magnetic (of yin- and yang-ultrons composite) and an electrical particle (of yin-or yang-ul- trons) [37] [44] [45] .
Further research would be needed for verification of the above findings and presentation.
Cite this paper
Chung, S.J. (2017) Comparison of Mathematical Equations Applicable to Tolerance of Total Body Irradiation in Humans and Decay of Isotopes, Uranium and Thorium: Differences and Similarity. J. Biomedical Sci- ence and Engineering, 10, 273-286. https://doi.org/10.4236/jbise.2017.105021
References
- 1. Cerveny, T.J., MacVittie, T.J. and Young, R.W. (1989) Acute Radiation Syndrome in Humans. In: Walker, R.J. and Cerveny, T.J., Eds., Medical Consequences of Nuclear Warfare, TMM Publications, Office of Surgeon General, Ellis Church, Virginia.
- 2. Jones, T.J., Morris, M.D., Wells, S.M. and Young, R.W. (1986) Animal Mortality Resulting from Uniform Exposure to Photon Radiation: Calculated LD50 and a Compilation of Experimental Data. Oak Ridge National Laboratory, Oak Ridge, TN.
https://doi.org/10.2172/6940829 - 3. Nènot, J. (2009) Radiation Accidents over the Last 60 Years. Journal of Radiological Protection, 29, 301-329.
https://doi.org/10.1088/0952-4746/29/3/R01 - 4. Abrahamson, S., Bender, M.A., Boecker, R.B. and Smith, J.M. (1993) Heath Effects Models for Nuclear Power Plant Accident Consequence Analysis. Government Printing Office, Washington DC.
- 5. Donnelly, E.H., Nemhauser, J.B., Smith, J.M., Kazzi, J.N., Fārfan, E.B., Chang, A.S. and Naeem, S.E. (2010) Acute Radiation Syndrome: Assessment and Management. Southern Medical Journal, 103, 541-544.
- 6. Baverstock, K and Williams, D. (2006) The Chernobyl Accident 20 Years on: An Assessment of the Health Consequences and the International Response.
http://www.scielo.br/pdf/csc/v12n3/19.pdf - 7. Baverstock, K.F. and Ash, F.J.D. (1983) A Review of Radiation Accidents Involving Whole Body Exposure and the Relevance to the LD50/60 for Man. British Journal of Radiology, 56, 837-849.
https://doi.org/10.1259/0007-1285-56-671-837 - 8. Warren, S. (1961) The Pathology of Ionizing Radiation. Charles C. Thomas Publishers, Springfield.
- 9. Van Middlesworth, L. (1989) Worldwide Iodine Fallout in Animal Thyroid, 1954-1987. In: Radiation and the Thyroid, Excerpta Media, Amsterdam, Princeton, Hong Kong, Tokyo, Sydney, 36-56.
- 10. Park, D. (2005) Introduction to Quantum Theory. 3rd Edition, Dover Publications, Inc., New York.
- 11. Griffiths, D. (2013) Introduction to Quantum Mechanics. Pearson, New Delhi.
- 12. Chung, S.J. (1960) Studies on a Mathematical Relationship between Stress and Response in Biological Phenomena. Republic of Korea Journal of National Academy of Sciences, 2, 115-162.
- 13. Chung, S.J. (1986) Computer-Assisted Predictive Mathematical Relationship among Metrazol and Time and Mortality in Mice. Computer Methods and Programs in Biomedicine, 22, 275-284.
https://doi.org/10.1016/0169-2607(86)90004-0 - 14. Chung, S.J. (1995) Formulas Expressing Life Expectancy, Survival Probability and Death Rate in Life Table at Various Ages in US Adults. International Journal of Bio-Medical Computing, 39, 209-217.
https://doi.org/10.1016/0020-7101(94)01068-C - 15. Chung, S.J. (2007) Computer-Assisted Predictive Formulas Expressing Survival Probability and Life Expectancy in US Adults, Men and Women, 2001. Computer Methods and Programs in Biomedicine, 86, 197-209.
https://doi.org/10.1016/j.cmpb.2007.02.009 - 16. Chung, S.J. (2013) Mathematical Relationship of “Probacent”-Probability Equation among Exogenous Stressor, Stress and Response in Biomedical Phenomena. International Journal of Education and Research, 1, 1-32.
http://www.ijern.com/September-2013.php - 17. Chung, S.J. (1988) Formula Expressing Carboxyhemoglobin Resulting from Carbon Monoxide Exposure. Veterinary and Human Toxicology, 30, 528-532.
- 18. Chung, S.J. (2011) Computer Program of Nonlinear, Curved Regression for “Probacent”-Probability Equation in Biomedicine. Journal of Biomedical Science and Engineering, 4, 620-630.
http://www.scirp.org/journal/jbise
https://doi.org/10.4236/jbise.2011.49078 - 19. Hastings Jr., C. (1955) Approximation for Digital Computer. Princeton University Press, Princeton, NJ, 185.
https://doi.org/10.1515/9781400875597 - 20. Chung, S.J. (2009) Seeking a New World: A New Philosophy of Confucius and Kim Hang. iUniverse, Bloomington, Indiana, 68-76.
- 21. Chung, S.J. (1989) Computer-Assisted Predictive Mathematical Relationship among Plasma Acetaminophen Concentration and Time after Ingestion and Occurrence of Hepatotoxicity in Man. Computer Methods and Programs in Biomedicine, 28, 37-43.
https://doi.org/10.1016/0169-2607(89)90179-X - 22. Chung, S.J. (1993) Formula Predicting Survival Probability in Patients with Heart Transplantation. International Journal of Biomedical Computing, 32, 211-221.
https://doi.org/10.1016/0020-7101(93)90015-X - 23. Chung, S.J. (1994) Formulas Expressing Relationship among Lesion Thickness and Time after of Diagnosis and Survival Probability in Patients with Malignant Melanoma. International Journal of Biomedical Computing, 37, 171-180.
https://doi.org/10.1016/0020-7101(94)90139-2 - 24. Chung, S.J. (1994) Formulas Expressing Relationship among Age, Height and Weight, and Percentile in Saudi and US Children of Aged 6 - 16 Years. International Journal of Biomedical Computing, 37, 259-272.
https://doi.org/10.1016/0020-7101(94)90124-4 - 25. Mehta, S.C. and Joshi, H.C. (2004) Model Based Point Estimates of Survival/Death Rates: An Input for Radiation Risk Evaluation in Indian Context. Indian Journal of Nuclear Medicine, 19, 16-18.
- 26. Chung, S.J. (2011) Predictive Formulas Expressing Relationship among Dose Rate, Duration of Exposure and Mortality Probability in Total Body Irradiation in Humans. Journal of Biomedical Science and Engineering, 4, 497-505.
http://www.scirp.org/journal/jbise
https://doi.org/10.4236/jbise.2011.47063 - 27. Chung, S.J. (2013) Computer Program of Linear Regression for “Probacent” Model Predicting Human Tolerance to Total Body Irradiation. International Journal of Education and Research, 1, 1-12.
http://www.ijern.com/images/May-2013/01.pdf - 28. Oregon State University. Radiation Decay Kinetics.
http://oregonstate.edu/instruct/ch374/ch418518/Chapter%203.pdf - 29. Perlman, I. and Rasmussen, J. (1957) Alpha Radioactivity. In: Encyclopedia of Physics, Vol. 42, Springer, New York.
https://doi.org/10.1007/978-3-642-45878-1_2 - 30. Chung, S.J. (1959) Studies of Positive Radial Acceleration on Mice. Journal of Applied Physiology, 14, 52-54.
- 31. Kim, C.C. and Chung, S.J. (1962) Studies on Relationship between Intensity of Stress, Duration of Exposure and Occurrence of Response in Goldfish Exposed to Single, Double and Triple Stress of Acceleration, Electroshock, Heat, Chemical and Osmotic Stimuli. Theses of the Catholic Medical College, Republic of Korea, 5, 257-336. (In Korean and English)
- 32. Hur, B. and Chung, S.J. (1962) Studies on Relationship between Dose, Time, and Percentage of Occurrence of Response in Drugs. New Medical Journal Korea, 5, 141-188.
- 33. Chung, S.J. (2011) Predictive Formulas Expressing Relationship between Dose Rate and Survival Time in Total Body Irradiation in Mice. Journal of Biomedical Science and Engineering, 4, 707-718.
http://www.scirp.org/journal/jbise
https://doi.org/10.4236/jbise.2011.411088 - 34. Chung, S.J. (2012) Computer-Assisted Formulas Predicting Cancer Mortality Risk after Exposure to Acute Low Dose Ionizing Radiation in Humans. Journal of Biomedical Science and Engineering, 5, 176-185.
http://www.scirp.org/journal/jbise
https://doi.org/10.4236/jbise.2012.54023 - 35. Chung, S.J. (2014) Self and Consciousness: Mind and Matter. International Journal of Education and Research, 2, 1-28.
http://www.ijern.com/March-2014.php - 36. Chung, S.J. (2014) Parallels between Confucian Philosophy and Quantum Physics. Open Journal of Philosophy, 4, 192-206.
http://www.scirp.org/journal/ojpp - 37. Chung, S.J. (2015) On the Possible Deeper Structure of Leptons and Quarks: A Review of the “Ultron”-“Logotron” Theory. Open Journal of Philosophy, 5, 302-314.
http://www.scirp.org/journal/ojpp/
https://doi.org/10.4236/ojpp.2015.55038 - 38. Palus, S. (2017) Electrons “Split” in New Form of Matter. Discover, January/February, Oak Ridge National Laboratory, Oak Ridge, TN, 27.
http://discovermagazine.com/2017/January/18-electrons-split-in-new-form-of-matter - 39. Piazza, B.D., Mourigal, L., Christensen, N.B., Nilsen, G.J., Trigenna-Piggott, P., Perring, T.G., Enderle, M., McMorrow, D.F., Ivanov, D.A. and Rφnnow, H.M. (2015) Fractional Excitations in the Square-Lattice Quantum Antiferromagnet. Nature Physics, 11, 62-68.
https://arxiv.org/abs/1501.01767 - 40. Paul Scherrer Institut (2012) Physicists Observe the Splitting of an Electron inside a Solid.
http://www.psi.ch/media/physicists-observe-the-splitting-of-an-electron-inside-a-solid - 41. Cui, Y., Hisha, H., Yang, G., Fan, T., Jin, T., Li, Q., Lian, Z. and Ikehara, S. (2002) Optimal Protocol for Total Body Irradiation for Allogenic Bone Marrow Transplantation in Mice. Bone Marrow Transplantation, 30, 843-849.
https://doi.org/10.1038/sj.bmt.1703766 - 42. Sacher, G.A. (1960) On the Relation of Radiation Lethality to Radiation Injury and Its Relevance for the Prediction Problem. IXth International Congress of Radiology, München, 23-30 December 1959, 1223-1232.
- 43. Limoli, C.L. (2017) Deep-Space Deal Breaker. Scientific American, 316, 54-59.
https://doi.org/10.1038/scientificamerican0217-54 - 44. Chung, S.J. (2017) A Review of the Ultron-Logotron Theory: Consciousness and Quantum Physics. International Journal of Humanities and Social Science, 7, in progress.
- 45. Shee, S.B. (2017) How Did the Proton Get Its Spin?
https://phys.org/news/2017-03-proton.html
Appendix
Equation (31) is derived from Equation (4a) (see the author’s previous publication [14] .


where P is probacent; D is death rate, t is time (age), a, b, A’, B’, γ and c are constants.


Equation (7) and Equation (32) are thus derived from Equation (4a).
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jbise@scirp.org










