Journal of Biomedical Science and Engineering
Vol.08 No.03(2015), Article ID:54825,13 pages
10.4236/jbise.2015.83017
Reliability and Precision Are Optimal for Non-Uniform Distributions of Presynaptic Release Probability
Jean-Marc Fellous1,2*, Nadia S. Corral-Frías1
1Graduate Interdisciplinary Program in Neuroscience, University of Arizona, Tucson, USA
2Department of Psychology and Applied Mathematics, University of Arizona, Tucson, USA
Email: *fellous@email.arizona.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 December 2014; accepted 12 March 2015; published 19 March 2015
ABSTRACT
Most conceptual and computational models assume that synaptic transmission is reliable, a simplification rarely substantiated by data. The functional consequences of the recruitment of high and low initial release probability synapses on the reliability and precision of their postsynaptic targets are studied in a multi-compartmental model of a hippocampal CA1 pyramidal cell. We show that changes in the firing rate of CA3 afferent inputs (rate remapping) are not reflected in the firing rate of the CA1 cell but in the reliability and precise timing of some of its action potentials, suggesting that a signature of remapping may be found in the precise spike timing of CA1. Our results suggest that about half of the action potentials produced by a CA1 cell can potentially carry reliable information in their precise timing with about 25 ms precision, a time scale on the order of the gamma cycle. We show further that reliable events were primarily elicited by CA3 synapses in a state of low probability of release. Overall, our results suggest that the non-uniform distribution of initial release probabilities observed experimentally achieves an optimum yielding simultaneously high precision and high reliability, and allows large populations of CA3 synapses to contribute to the production of reliable CA1 spiking events.
Keywords:
Spike Timing, Hippocampus, Computational Model, Synapses

1. Introduction
In vivo, hippocampal and cortical cells receive a large amount of background subthreshold synaptic inputs in addition to information rich inputs to which they respond by emitting action potentials. CA1 pyramidal cells are well known to contribute to a precise code for spatial location. Several lines of experimental evidence suggest that the precise generation of action potentials in the hippocampal region CA1 may have functional significance.
Studies in vitro suggest that the precise timing (10 - 20 ms) of pre and post synaptic activation may result in long-term increases or decreases in synaptic strength [1] [2] . Precise and reliable firing can be achieved in vitro by current injection at the soma [3] and is highly dependent on the frequency content of the stimulus [4] . There is evidence in vivo that information about the position of an animal within a CA1 place field might be carried by the precise timing of action potential generation with respect to theta oscillations, a phenomenon termed phase precession [5] . For a CA3 or CA1 place cell to phase-precess, the firing displacement from cycle to cycle should be tightly controlled within temporal windows on the order of 10 - 20 ms. Finally, it has been shown that pyramidal cells in hippocampus or cortex can precisely fire relative to each other during periods of reactivation in sleep or quiet wakefulness [6] - [8] , again on time scales of a few tens of milliseconds.
Several theories have been proposed to explain how reliability and precision emerge from presynaptic correlations or strong synapses [9] [10] . Only a few of these theories take into account the stochastic and highly dynamical nature of the synaptic probability of release and its heterogeneity among synapses impinging upon the same cell [11] [12] . How this probability of release and its short term dynamics allow for the reliable and precise generation of action potentials in the face of large amounts of background noise is still poorly understood. One possibility is that reliable firing events occur if the average probability of release of background information- poor and signal information-rich synapses is different.
To study the conditions in which stochastic synaptic transmission allows for the generation of reliable and precise spikes trains, we use the well-studied CA3-CA1 pathway where the biophysical details of synaptic trans- mission, synaptic integration and action potential generation are well understood and quantified. In this system, CA3 Schaffer collateral synapses (CA3 to CA1 axons in the stratum radiatum) have an average release probability on the order of 25% [13] [14] and exhibit a non-uniform distribution of initial probability of release, with some synapses significantly more reliable than others [13] - [16] . We built a multi-compartmental biophysical model of a reconstructed CA1 pyramidal cell contacted by CA3 AMPA/NMDA stochastic synapses that included facilitation and depression. We investigated the functional consequences of the recruitment of high and low initial release probability CA3 synapses on the reliability and precision of CA1 pyramidal cells.
2. Materials and Methods
All simulations were performed using the NEURON simulator [17] with a time step of 0.1 ms. Data analyses were conducted in Matlab using custom written software.
2.1. Cell Morphology
To illustrate the consequence of recruiting high or low probability synapses on the output of a cell, we use a simplified single compartment model (Figure 1). This “ball neuron” contains all the currents of the multi-com- partment cell, tuned so that input resistance and membrane potential are within 5% of that of the multi-com- partment cell. We then used a reconstructed multi-compartmental CA1 cell from the Duke/Southampton cell archive (cell n180). This cell was chosen to represent the typical cell population available in terms of surface area and branching structure (cells n400 and n123 were also studied, but are not discussed here for simplicity). The cell membrane area was 74,686 μm2, and contained about 600 compartments (Figure 2(b)). The cell surface was corrected to account for spines [18] . Further details are given in Supporting Information.
2.2. Cell Physiology
The dendritic compartments were devoid of active currents, except for their aggregate influence on the membrane potential near rest (sigmoid leak conductance). This modeling choice was motivated by the desire to stay simple and independent from particular assumptions on the nature and densities of the many currents known to be present in dendrites [19] , and by the finding that in spite of all these currents, the synaptic summation in CA1 dendritic trees was essentially linear [20] . Also, most of the simulations were performed with small numbers of synapses, under conditions where spontaneous background synaptic activity was minimal. In these conditions, the dendritic membrane potential was presumably undergoing small fluctuations near rest, and hence
Figure 1. Response (50 trials) of a simplified model neuron to a signal embedded in background noise. The signal is carried by 30/500 AMPA/NMDA synapses (inset). The initial probability of release (p0) of all Background or all Signal inputs are set at two levels (Low: p0 = 0.28, High: p0 = 0.65) and the four combinations of Background/Signal probability of release are shown in the four panels and graphically depicted under each rastergram. (a) Background-High, Signal-Low; (b) Background-High, Signal-High; (c) Background- Low, Signal-Low; (d) Background-Low, Signal-High. In all panels the signal-to-noise (SNR) ratio is indicated and the gray areas mark the time interval when the response of the cell is expected and where the SNR is computed.
was unlikely to trigger significant active voltage-dependent excursions beyond those captured by the non-uni- form leak conductance. Further work would be needed to assess the role of specific dendritic current combinations [21] . Quantitative details on the cell physiology parameters are given in Supporting Information.
As will be described below, the model of the synapse was tuned on the basis of in vitro experimental work. Our simulations, however, aim at explaining in vivo phenomena. We assume that synaptic releases dynamics are similar in vivo and in vitro, but we adjust the intrinsic parameters of the CA1 cells to what is known from in vivo experiments. Details on these adjustments are given in Supporting Information.
2.3. Synaptic Physiology
2.3.1. Time Scale Limitations
In CA1, excitatory synapses exhibit short term facilitation and depression that are mainly the result of short term changes in the probability of release. These changes can occur at time scales in the range of 8 - 25 ms [15] [22] . At these time scales the effects of facilitation and depression are highly variable at individual synapses and a
Figure 2. (a) Distribution of initial release probability of 5000 model synapses (see methods). The red curve shows the gamma curve obtained experimentally [35] ; (b) Reconstructed CA1 multi-compartmental cell used in this study (Duke/Sou- thampton cell archive, n180). Dashed lines indicate the sections of the dendritic tree where CA3 synapses were distributed; (c) CA1 mean in-field firing rate for 10 random distributions (remappings) of CA3 presynaptic spike times on 500 synapses. Synapse locations are identical. Presynaptic CA3 spike times were taken from the experimental data of Leutgeb et al. 2004. There are no significant differences in firing rates between any two of the 10 firing rates. P > 0.05 for all pairs (student t-tests); (d) Sample rastergrams from two of the remappings 1 and 2 in C showing that while firing rates are nearly identical, precise spike timing events spontaneously emerge in the course of the simulations. Closed arrows: reliable spike time event common to the two remappings, open arrows reliable spike time events specific to each remappings. Reliability (R) and Precision (P) are indicated for each rastergram (see methods).
clear understanding of the underlying mechanism is yet to be achieved. At time scales larger than 40 ms, consistent data on facilitation and depression can be found in the hippocampus [13] [23] . Synaptic dynamics also change on the time scales of seconds to minutes. Post-tetanic potentiation, augmentation and other long term effects (LTP and LTD) have been extensively studied, and may be of importance for long lasting phenomena such as those implicated in learning, or for conditions where long presynaptic spike trains are evoked. Because we focus on neural activity that last at most 2 or 3 seconds and involve short spike trains (2 - 20 spikes, traversal of a place field), we restrict our model to synaptic dynamics that have time constants in the 40 ms - 2 sec time range. Note also that in choosing specific sets of in vitro experimental data to tune our model, care was taken to only use experimental conditions that are compatible, especially when pertaining to extracellular concentrations of calcium and magnesium.
2.3.2. Modeling Assumptions and Choices
The dynamic stochastic synapse we used was based on previous experiments using minimal stimulation and inspired by other theoretical formulations [24] [25] . The model assumes that at most one vesicle is released per presynaptic action potential [26] [27] , and that if one afferent axon makes multiple synapses on the same postsynaptic target, these synapses are independent.
As for all models, a balance needs to be stricken between complexity (biophysical realism) and explanatory power. In designing the model, we opted for a formulation in which facilitation and depression are two independent entities, each with their own time constant and magnitude (4 parameters), that can be fully constrained by physiological data. Furthermore, because experimental evidence suggested that the heterogeneity of synaptic dynamics in CA1 glutamatergic synapses was related to initial release probability, we made this probability an explicit variable [28] . We did not explicitly model synaptic calcium dynamics, which is an important factor underlying these two forms of short term plasticity [29] - [31] partly because our emphasis is on single synapse stochasticity and because data on calcium dynamics are mainly applicable to phenomenological (average) models. However, we show below that after proper parameter adjustment, this model gave good fits to data that were not used to tune it.
Most of the experimental data gathered on synaptic transmission in vitro was obtained at room temperature (e.g. [13] [15] [32] ). Accordingly, we built, tuned and validated our model of synaptic transmission using datasets obtained at room temperature from different laboratories. We note that some differences in tuning may result if the temperature is raised to physiological levels [33] . We did not find sufficient published data obtained at physiological temperatures to simultaneously tune and validate our model, especially using the minimal stimulation technique. We however compensated for the temperature discrepancy by adjusting the physiological characteristics of CA1 firing to mimic that obtained in vivo in the anesthetized animal (see “cell physiology” above).
Finally, because we intend to make quantitative predictions about the relationship between the stochasticity of Schaffer collateral synapses and the firing of CA1 pyramidal cells, we use different datasets from different laboratories to separately adjust and validate the model parameters. Validation is taken here to mean the generation of predictions that have been confirmed experimentally in studies and protocols that have not been used to adjust the model.
2.4. Model of Stochastic Release
The probability of release of a single synapse was given by the equation
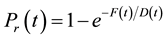 (1)
(1)
where F and D are time-dependent variables representing facilitation and depression, respectively. At each excitatory synapse, when a presynaptic spike is received at time t, a random number from a uniform distribution is drawn and the probability of release, Pr(t), is calculated based on the current release history S (the subset of presynaptic spike times at which the synapse has indeed released). If the random number is larger than Pr(t), a postsynaptic potential is generated, and S is updated. Note that it is not necessary to update Pr(t) for each synapse at every simulation time increment but only when a presynaptic spike occurs at that synapse.
Each individual synapse had five parameters: The unitary conductance, the initial amount of facilitation and depression (F0 and D0 respectively), the amount of facilitation produced by a single presynaptic action potential (Fmag), and the amount of depression resulting from a single release (Dmag). Details on the explicit formulations for F(t) and D(t), and on the tuning of their parameters are given in Supporting Information.
2.5. Distribution of Initial Release Probabilities
The initial release probability (p0) is not uniform across hippocampal synapses in the same CA1 pyramidal cell (Figure 2(b) shows the cell used in this study), as well as on average across many such cells [22] [34] -[36] . The distribution is well described by a gamma function of the form:
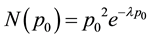 (2)
(2)
where N(p0) is the number of synapses with initial probability p0, and λ (here λ = 10.7) is a constant such that the average probability across all synapses of this distribution is about 0.28 [35] . With D0 = 1 by convention,
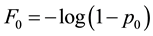 and the distribution of F0 is completely defined by the distribution of initial release probabilities p0.
and the distribution of F0 is completely defined by the distribution of initial release probabilities p0.
Figure 2(a) shows the distribution of initial release probabilities resulting from the random draw of 5000 F0 values constrained by p0 as described above, together with the fit given by experimental data [35] .
2.6. Postsynaptic Synaptic Currents
Excitation: The dynamics of the postsynaptic AMPA current was obtained upon release using a two state kinetic scheme, NMDA channels were similarly modeled with 5 states, including desensitization and re-sensitization [37] .
Inhibition: The simulations conducted here used real CA3 spike trains recorded in vivo while animals traversed a place field. Inhibitory cells in the cell body layer typically do not show place specificity [38] , and in the time course of the traversal can be considered tonically active. Due to the complexity of the inhibitory cell population and the lack of detailed data on GABAergic synaptic transmission (e.g. depression, facilitation), we opted for a simplified implementation of feed forward inhibition. Inhibition was represented by an Ornstein- Uhenbeck process inserted in all compartments of the soma, as in previous work [39] [40] .
Details on the tuning of the synaptic conductances and their validation are given in Supporting Information.
2.7. Input Spike Trains
In order to provide our model with realistic inputs, we use data provided by S. Leutgeb and published elsewhere [41] . The inputs spike trains to our model CA1 cells were taken from a population of 37 CA3 pyramidal cells recorded simultaneously in four 10 minutes sessions, as the animal was exploring a rectangular box [41] . In most simulations we chose random sets of 500 of these real spike trains to simulate a realistic CA1 input. Details on the input spike trains, and justification for this number of spike trains are given in Supporting Information.
2.8. Reliability and Precision
In order to assess the extent to which the response of a CA1 cell is reliable, we repeat all simulations 40 times, with the same presynaptic CA3 spike trains, but with different seeds for the stochasticity of the synapses. It is unlikely that, in vivo, the exact same presynaptic pattern of activation reoccurs, so these simulations are not meant to represent a realistic case. The goal of these repeated stimulations is to identify which spikes (if any) of the CA1 cell are potentially specific to the presynaptic pattern of activation, and therefore potential carrier of in- formation about the input. These CA1 spikes would be re-emitted more often than chance during the 40 presen- tations. Other spikes would not. These reliable patterns of spiking are visually detectable as alignments in the rastergram of the CA1 response across the 40 trials (“Events”, Figure 3 arrows). To quantify their occurrence we use the “direct method” for the computation of reliability and precision [10] . Details on these computations are given in Supporting Information.
3. Results
To investigate how the short term dynamics of the probability of release allow for the reliable and precise generation of action potentials, we first used the simplified biophysical ball neuron (Figure 1, center inset, see methods for details). The simulations show that the worst Signal-to-Noise Ratio (SNR) is achieved when background synapses have high release probability and signal synapses have low release probability (Panel A, BkgHigh/SigLow, SNR
Figure 3. Reliability and precision for three different distributions of initial probability of release. (a) GP is the Gamma distribution obtained experimentally (Figure 1(b)), LP is a Gaussian distribution of the same mean as GP but not including high probability synapses (tail of GP), HP is a Gaussian distribution of mean 0.65 which does not include low probability synapses; (b) Reliability; (c) Precision. All simulations results were obtained with 500 synapses. Each bar is obtained on the basis of 15 different presynaptic spike patterns obtained from the CA3 data (see methods and supplemental information), repeated 40 times. *p < 0.05, **p < 0.01 (student t-tests).
= 0.03). Note the emergence of spurious reliable events as alignments across multiple trials (arrows). These events are due to the random occurrence of nearly synchronous spike times in several background synapses (the synapses responsible for the different events are not necessarily identical). If the probability of signal synapses is raised to the same level as that of the background, the cell emits a reliable event at the appropriate time (Figure 1(b), gray box), but several others at unwanted times, yielding a low SNR (Panel B, BkgHigh/SigLow, SNR = 0.13). If both background and signal synapses are low, very few spikes are emitted, the cell is unresponsive except on a very few trials and the SNR is again low (Panel C, BkgLow/SigLow, SNR = 0.26). The best SNR is obtained when the background probability of release is low and the signal probability of release is high (Panel D, BkgLow/SigHigh, SNR = 0.61). These results suggest that for precisely and reliably timed events to be produced in a population of synapses of identical potency (same somatic EPSC size), the information has to be selectively routed on synapses with high release probability. This result is puzzling on three accounts: First it is difficult to imagine how such a specific synapse selection might occur dynamically, accounting for dendritic filtering and for the highly variable process of information transmission. Second, the population of high probability synapses, at least in the hippocampus CA3-CA1 pathway, is very small, severely limiting the amount of “signal” channels available (Figure 2(a)). Third, the synaptic probability of release is a highly dynamical variable that changes on the times scale of milliseconds as synapses undergo depression and facilitation, so that signal transmission should be appropriately timed to reach the synapse when its probability of release is high.
3.1. Spike Rate vs. Spike Timing
The CA3-CA1 pathway was used to study the conditions in which stochastic synaptic transmission allow for the generation of reliable and precise spikes trains. We assessed the response of a reconstructed CA1 cell to inputs representing the traversal of a place field. To ensure that the pattern of presynaptic inputs was as close as possible to in vivo data, the inputs spike trains to the model cell were taken from a population of 37 CA3 pyramidal cells recorded simultaneously in four 10 minutes sessions, as a rodent explored a rectangular box [41] . For each cell, place fields were characterized using video tracking data (single place fields, all data kindly provided by Dr. S. Leutgeb). Each traversal of each place field of each cell was isolated, and the corresponding spike trains were collected (992 spike trains, mean in field discharge was 4.7 Hz range 0.1 - 20 Hz, see supplemental material).
Figure 2(c) shows the firing rate variability of the CA1 cell across 10 different sets of presynaptic CA3 spike trains. Each spike train was randomly assigned to one of 500 synapses distributed randomly in the compartments of the CA1 cell within the stratum radiatum area. Forty trials per presynaptic spike time set were simulated (error bars). The 10 redistributions of presynaptic spike trains simulated 10 different rate remappings in CA3 [42] . No significant difference in CA1 firing rate were detected across any of the conditions (paired t-tests p > 0.1), suggesting that CA3 rate remapping cannot yield CA1 rate remapping through the type of stochastic synapses used here, consistent with experimental data [43] . We further used these 40 trials to assess the extent to which timing information may be present as “events” across trials. If indeed a subset of CA1 action potentials are a consequence of some specific aspects of the CA3 presynaptic inputs (e.g. synapse locations, pattern of presynaptic spike times, synapse initial release probability), then some of the CA1 spikes should occur reliably across multiple trials ran with identical CA3 presynaptic input patterns. Panel 2D shows the rastergrams resulting from two of the remappings shown in Panel A (1 and 2). It is clear from these simulations that, even though the CA1 cell firing rates are not different across the 40 trials, timing information is present (arrows), and some reliable spike times emerge, as with our simple model (Figure 1(a), Figure 1(b), Figure 1(d)). Some reliable spike times are common to the two rate remappings (dark arrows, Panel 2D), others are specific to the pattern of CA3 presynaptic times being used (open arrows, Panel 2D). This result suggests and predicts that while rate remapping in CA3 may not be reflected in the firing rate of a specific CA1 cell, some signature of the remapping may be found in its precise spike timing.
Since the nature of the “signal” and “background” is unknown, we used measures of reliability and precision to quantify the emergence patterns of spike times rather than SNR ([10] and see methods). Reliability measures the consistency of firing at specific times from trial to trial (0 < R < 1, 1 very reliable) and precision is inversely proportional to the average jitter of firing around reliable spike times (expressed in Hz, high frequency is high precision). The rastergrams in Figure 2(d) had a reliability and precision of 0.33 and 57 Hz (1, top) and 0.43 and 41.5 Hz (2, bottom) respectively. The mean reliability and precision for all the remapping simulations in Figure 2(c) were 0.47 ± 0.1 and 40 ± 15 Hz respectively. Almost half (47%) of all spikes belonged to events (alignments across trials, as in arrows in Figure 2(d)) and the average temporal jitter of these alignment was 25 ms. These results suggest that about half of the spikes produced by the modeled CA1 can potentially carry reliable information in their precise timing within 25 ms precision, a time scale on the order of the gamma cycle.
3.2. Contribution of High and Low Probability Synapses to Precision and Reliability
In this model, the variability of the CA1 response is due to the stochasticity of the synapses. Unlike most models, and compatible with experimental data, synapses here have different initial release probabilities distributed along a tailed gamma-like distribution function (Figure 2(a)). In this distribution, most synapses have a low probability of release (around 0.28), and a few synapses have a high release probability (above 0.5). In order to assess the extent to which reliability and precision depend on initial release probability, we repeated the simulations above using a Gaussian distribution of low initial probabilities (0.28, Figure 3(a), dotted line, LP) which did not include any high probability synapse, a gamma distribution as observed experimentally (Figure 3(a), continuous line, GP) and a Gaussian distribution with higher mean (0.65, Figure 3(a), dashed line, HP), which did not include low probability synapses. The conductances of all synapses were equal and adjusted so that the average firing rate of the CA1 cell was identical in the three conditions (about 3.5 Hz, as in the data, see supplemental methods). Perhaps counter-intuitively, the reliability of the CA1 response was lowest in the case of the Gaussian with high mean initial release probability (white bars HP), and highest in the case of the Gaussian distribution with the lowest initial release probabilities (LP) (Figure 3(b)). This result may stem from the fact that high probability synapses make the CA1 cell more sensitive to non-synchronous presynaptic inputs. Such spikes occur outside events, and hence decrease the reliability. On the other hand, low probability synapses only allow the CA1 cell to fire when it receives a sufficiently synchronous presynaptic input volley. The results presented here suggest that if a neural code uses synchrony as a way of conveying information, too many high probability synapse would make the CA1 cell sensitive to noise (i.e. non synchronous inputs), while low probability synapses would make the cell sensitive to the “signal” (i.e. synchronous inputs). Figure 3(c) also shows the precision for these three release probability distributions. Precision is highest for the HP distribution, and lowest for the LP distribution. The Gamma distribution (GP) therefore achieves a compromise between high and low values for both precision and reliability. This result is compatible with the results shown in the simple model (Figure 1(d), BkgLow/SigHigh) in which the SNR is the highest, and in which the distribution of presynaptic release probability is double peaked with the majority of synapses having low probability, and a few having high probability. In the CA1 simulation however, synaptic dynamics are such that the release probability of a synapse at the time of an event is not necessarily high, as in Figure 1(d).
In order to determine which synapses are responsible for events, we plotted the presynaptic CA3 spike trains around a representative CA1 event (Figure 4). This plot allows for the global visualization of when CA3 spikes were received at which synapses, just before the CA1 cell fired reliably (firing of CA1 is not shown for clarity, the time of reliable firing is indicated by the vertical red line). Figure 4(a) shows the CA3 spike trains for all 500 synapses, 100 ms around the time of occurrence of a CA1 event (vertical red line). In this plot, the initial probability of release is pulled from a Gaussian distribution of mean 0.28 (LP, black bars in 3B, C). The inset shows the distribution of initial probabilities. The synapses are sorted in increasing order of release probability at the time of the event, so that synapse #0 had the lowest release probability at the time marked by the vertical red line (here, p = 0.02), and synapse #500 had the highest probability of release (here, p = 0.77). This graph demonstrates that two distinct populations of synapses were involved in the triggering of this event: a small group of synapses in a state of low release probability (100 synapses, between indices 0 and 100, bottom grey box), and a group of synapses in a state of high probability (50 synapses between indices 450 and 500, top grey box). The other 350 synapses did not receive a significant number of presynaptic spikes and therefore did not contribute to the spiking at that specific event. This distribution of probability is similar to that of Figure 1(d) (BkgLow/SigHigh), even though all synapses started with low initial release probabilities (0.28, as in 1C, BkgLow/ SigLow). This result shows that the synaptic population self-organizes into an optimal (i.e. highest SNR) distribution of release probability and dynamically transitions from a BkgLow/SigLow type composition to a BkgLow/ SigHigh composition prior to a reliable event. Only a small fraction of synapses (150/500) actually contribute to each reliable event.
Figure 4(b) shows the presynaptic spike trains responsible for an event, when the initial probabilities of release were obtained from a Gaussian distribution of mean 0.65 (HP, white bars in Figure 3(b), Figure 3(c)). In
Figure 4. Presynaptic CA3 firing patterns before a representative CA1 event in the cases of synapses with initial probability of releases that are distributed as a Gaussian around 0.28 (a) and Gaussian around 0.65 (b). Synapses are ordered according to their instantaneous probability of release at the time of the event (red vertical line). Index 0 corresponds to the lowest probability. Insets are as in Figure 3(a). Grey boxes highlight the synapses and presynaptic spikes contributing to the event.
this case, the population of synapses that was responsible for this CA1 event is single-peaked and includes synapses in a state of low probability of release at the time of the reliable event (150 synapses, numbered between 0 to about 150, grey box), even though all synapses had initially a strong release probability (as in Figure 1(b), BkgHigh/SigHigh). At the time of the event, however, all synapses were strongly depressed. This result is analogous to that of Figure 1(c) ―BkgLow/SigLow, in that if an event occurs, its reliability is low but it is precise (Figure 3(b), Figure 3(c), HP). These results show that the population of synapses dynamically transitions from a population of type BkgHigh/SigLow (Figure 1(b)) to that of type BkgLow/SigLow (Figure 1(c)) just before an event. Again, only a small fraction of synapses (150/500) contribute to the event. Interestingly, the transition does not evolve further to type BkgLow/SigHigh (Figure 1(d)) as would be expected from the results of Figure 4(a), keeping the events precise but low reliability.
To quantify these observations, we collected simulation results across events, and across different presynaptic distributions (i.e., 10 rate remappings). In these simulations the membrane time constant of the CA1 cell was 24 ms, and the lowest event precision was about 40 Hz (i.e. jitter of 25 ms). This suggests that CA1 spiking is likely due to presynaptic CA3 inputs arriving less than 50 ms before a CA1 spike. We plotted the average number of spikes occurring 50 ms before an event at each of the 500 synapses for the low probability distribution (LP; 47 events, Figure 5(a)). The average number of spikes received at a synapse within these 50 ms represents a measure of the contribution of a particular synapse to an event. The plot shows two peaks at synapses with low (Pre ~ 0, inset) and high (Pre ~ 0.4, inset) release probabilities at the time of the event. The inset shows that the overall distribution of release probability of all synapses at the time of the events was Gaussian-like, centered on low release probabilities (0.15). This suggests that at the time of events all synapses were strongly depressed. Figure 5(b) shows that a high initial release probability distribution HP (51 events) leads to a smoothly decaying distribution of presynaptic spikes where synapses with low release probabilities received more presynaptic spikes than synapses with higher release probability. The inset shows that the distribution of release probabilities at the time of events was approximately uniform, but limited to low releases (Pre ~ <0.4). Although all synapses had high initial release probabilities (HP is centered at 0.65), almost all synapses were depressed and contributed equally to the events. This group data confirms the conclusions reached on the basis of the representative example shown in Figure 4 and further indicates that unlike in Figure 1, reliable events were primarily elicited by synapses in a state of low probability of release.
The Gamma distribution of initial release probabilities observed experimentally allows for a tradeoff between high reliability and high precision (Figure 3(b), Figure 3(c), gray bars, GP), recruiting BkgLow/SigHigh probability synapses (Figure 1(d)) which would be optimal if the events were only triggered by high probability sy- napses. However, the analysis of the synapses contributing to an event (Figure 5(c)) performed here reveals a more homogeneous recruitment. The synapses responsible for events are in various states of release probability, with a bias for lower probabilities. Figure 5(d) shows the distribution across 10 CA3 rate re-mappings. The distribution is significantly more uniform than in panels A and B, with a slight bias for probabilities in the lowest 20% range (Pre < 0.15). This distribution contains an approximately equal number of spikes received by synapses with release probabilities between 0.15 and 0.95 at the time of the events. The inset shows that the overall distributions of probabilities at the time of the events was gamma-like (peak Pre = 0.12) with a few synapses with strong release probability (Pre > 0.5).
These results show that both low and high initial release probability synapses are required for the generation of events that are both reliable and precise. If high probability synapses are eliminated (LP), precision decreases and reliability increases. Events occur in response to the recruitment of depressed synapses with release probabilities on either flank of a Gaussian distribution. If low probability synapses are eliminated, reliability decreases (HP), but precision increases. Events occur in response to the recruitment of synapses in various states of low probability of release. The gamma-shaped distribution of initial probability of release (GP) realizes a tradeoff between reliability and precision. In that case, events occur in response to the uniform recruitment of most synapses.
4. Discussion
Overall, the results shown here suggest that the variability of CA1 cell responses observed in vivo during place field traversals [44] is at least in part due to the stochasticity and short term dynamics of Schaffer collateral synapses. In general, short term synaptic dynamics and spike-history dependence may have functional consequences. They can act as frequency filters [12] , presynaptic spike patterns detectors [45] controllers of the input-output gain of individual cells [46] [47] , sources of bistability [48] , and in general, increase the computational power of neural networks [24] [25] [49] . Previous work has shown that an increase in the amount of information transmitted is possible through the elimination of presynaptic spike train redundancies, using depressing synapses [50] [51] . These studies, and most conceptual and computational models, assume that the stochasticity of CA3 to CA1 synapses is uniform. Our results suggest that these models may need to be re-eva- luated in the light of the heterogeneity of synaptic transmission.
Figure 5. Average number of presynaptic spikes before an event for initial probability of releases distributed as a Gaussian centered at 0.28 (a), centered at 0.65 (b) and for the gamma distribution (d). (c) Representative presynaptic pattern around an event for the Gamma distribution GP. Panels A, B and D were each obtained for 500 synapses stimulated by 10 presynaptic patterns 40 times. Synapses are ordered by their instantaneous probability of release at the time of each event. The distributions in Panels A, B and D are obtained by subtracting the analogous distributions computed for random (non-aligned) events.
Before place field traversal, CA3 cells are essentially silent, therefore, when entering the place field, the CA3- CA1 synapses will release according to their initial release probability. Since different synapses have different initial probabilities of release [22] [34] -[36] , their patterns of release, and therefore their contribution to postsynaptic firing, are likely to be significantly different during the course of place field traversal. Our model predicts that the gamma-like shape of the initial release probability distribution achieved an optimum such that, in principle, all synapses could contribute to the reliable spiking of the CA1 cell. Gaussian distributions resulted in a de facto selection of sub populations of synapses, leaving a significant portion of synapses unlikely to contribute to reliable CA1 firing. Our results demonstrate therefore that the gamma-shaped distribution of initial release probability “normalizes” the inputs to CA1 so that all synapses can contribute to CA1 firing, an assumption commonly made, but never documented, in most conceptual and computational models of the CA3-CA1 pathway.
It has been suggested that some of the memory acquisition and consolidation mechanisms could be partly understood through the study of rate and global remapping [42] . Our model makes two additional sets of predictions. During this type of remapping, at least two presynaptic features can affect the firing rate of a CA1 cell during place field traversal: the number of synapses recruited and the mean firing rate of the presynaptic cells. We showed that a differential of 75 - 125 CA3 synapses or a change by at least 1.3 Hz in CA3 firing rates were necessary for the model CA1 cell to generate significantly different firing rates (Supplemental material). Our results also show that if CA3 alone was involved in eliciting CA1 action potentials, the number of CA3 cells involved in the traversal of one CA1 place field would be about 500 ± 200. In the case of rate remapping, a redistribution of CA3 presynaptic spike trains with little change in mean firing rate (i.e. less than 1.3 Hz) did not result in changes in CA1 firing rate (Supplemental material). Altogether, these results suggest the existence of global and rate remapping “thresholds” bellow which the hippocampal spatial code of the animal remains relatively stable. We furthermore demonstrate that, below these thresholds, information about the remapping can potentially be carried by the precise timing of a subset of CA1 spikes (“events” in our terminology, Figure 2). Further experiments could test this prediction by controlling the trajectory of the animal before and after rate remapping.
Acknowledgements
We thank Stefan Leutgeb and the Moser laboratory for kindly providing the CA1 and CA3 data used in this study. Supported in part by ONR grant N000141310672, NSF CRCNS 1010172 and NSF 1117388 to JMF and a CONACYT predoctoral fellowship to NCF. Supplemental information and figures can be found of the corresponding author’s website.
Cite this paper
Jean-MarcFellous,Nadia S.Corral-Frías, (2015) Reliability and Precision Are Optimal for Non-Uniform Distributions of Presynaptic Release Probability。 Journal of Biomedical Science and Engineering,08,170-183. doi: 10.4236/jbise.2015.83017
References
- 1. Bi, G.Q. and Poo, M.M. (1998) Synaptic Modifications in Cultured Hippocampal Neurons: Dependence on Spike Timing, Synaptic Strength, and Postsynaptic Cell Type. Journal of Neuroscience, 18, 10464-10472.
- 2. Campanac, E. and Debanne, D. (2008) Spike Timing-Dependent Plasticity: A Learning Rule for Dendritic Integration in Rat CA1 Pyramidal Neurons. The Journal of Physiology, 586, 779-793.
http://dx.doi.org/10.1113/jphysiol.2007.147017 - 3. Mainen, Z.F. and Sejnowski, T.J. (1995) Reliability of Spike Timing in Neocortical Neurons. Science, 268, 1503-1506.
http://dx.doi.org/10.1126/science.7770778 - 4. Fellous, J.M., Houweling, A.R., Modi, R.H., Rao, R.P., Tiesinga, P.H., et al. (2001) Frequency Dependence of Spike Timing Reliability in Cortical Pyramidal Cells and Interneurons. Journal of Neurophysiology, 85, 1782-1787.
- 5. Maurer, A.P. and McNaughton, B.L. (2007) Network and Intrinsic Cellular Mechanisms Underlying Theta Phase Precession of Hippocampal Neurons. Trends in Neurosciences, 30, 325-333.
http://dx.doi.org/10.1016/j.tins.2007.05.002 - 6. Sutherland, G.R. and McNaughton, B. (2000) Memory Trace Reactivation in Hippocampal and Neocortical Neuronal Ensembles. Current Opinion in Neurobiology, 10, 180-186.
http://dx.doi.org/10.1016/S0959-4388(00)00079-9 - 7. Lee, A.K. and Wilson, M.A. (2002) Memory of Sequential Experience in the Hippocampus during Slow Wave Sleep. Neuron, 36, 1183-1194.
http://dx.doi.org/10.1016/S0896-6273(02)01096-6 - 8. Wilson, M.A. and McNaughton, B.L. (1994) Reactivation of Hippocampal Ensemble Memories during Sleep. Science, 265, 676-679.
http://dx.doi.org/10.1126/science.8036517 - 9. Wang, H.P., Spencer, D., Fellous, J.M. and Sejnowski, T.J. (2010) Synchrony of Thalamocortical Inputs Maximizes Cortical Reliability. Science, 328, 106-109.
http://dx.doi.org/10.1126/science.1183108 - 10. Tiesinga, P., Fellous, J.M. and Sejnowski, T.J. (2008) Regulation of Spike Timing in Visual Cortical Circuits. Nature Reviews Neuroscience, 9, 97-107.
http://dx.doi.org/10.1038/nrn2315 - 11. Rotman, Z. and Klyachko, V.A. (2013) Role of Synaptic Dynamics and Het-erogeneity in Neuronal Learning of Temporal Code. Journal of Neurophysiology, 110, 2275-2286.
http://dx.doi.org/10.1152/jn.00454.2013 - 12. Kandaswamy, U., Deng, P.Y., Stevens, C.F. and Klyachko, V.A. (2010) The Role of Presynaptic Dynamics in Processing of Natural Spike Trains in Hippocampal Synapses. Journal of Neuroscience, 30, 15904-15914.
http://dx.doi.org/10.1523/JNEUROSCI.4050-10.2010 - 13. Dobrunz, L.E. and Stevens, C.F. (1997) Heterogeneity of Release Probability, Facilitation, and Depletion at Central Synapses. Neuron, 18, 995-1008.
http://dx.doi.org/10.1016/S0896-6273(00)80338-4 - 14. Allen, C. and Stevens, C.F. (1994) An Evaluation of Causes for Unreliability of Synaptic Transmission. Proceedings of the National Academy of Sciences of the USA, 91, 10380-10383.
http://dx.doi.org/10.1073/pnas.91.22.10380 - 15. Dobrunz, L.E., Huang, E.P. and Stevens, C.F. (1997) Very Short-Term Plasticity in Hippocampal Synapses. Proceedings of the National Academy of Sciences of the USA, 94, 14843-14847.
http://dx.doi.org/10.1073/pnas.94.26.14843 - 16. Alabi, A.A. and Tsien, R.W. (2012) Synaptic Vesicle Pools and Dynamics. Cold Spring Harbor Perspectives in Biology, 4, Article ID: a013680.
http://dx.doi.org/10.1101/cshperspect.a013680 - 17. Hines, M.L. and Carnevale, N.T. (1997) The NEURON Simulation Environment. Neural Computation, 9, 1179-1209.
http://dx.doi.org/10.1162/neco.1997.9.6.1179 - 18. Major, G., Larkman, A.U., Jonas, P., Sakmann, B. and Jack, J.J. (1994) Detailed Passive Cable Models of Whole-Cell Recorded CA3 Pyramidal Neurons in Rat Hippocampal Slices. Journal of Neuroscience, 14, 4613-4638.
- 19. Stuart, G., Spruston, N. and Hausser, M. (1999) Dendrites. Oxford University Press, Oxford, 376 p.
- 20. Cash, S. and Yuste, R. (1999) Linear Summation of Excitatory Inputs by CA1 Pyramidal Neurons. Neuron, 22, 383-394.
http://dx.doi.org/10.1016/S0896-6273(00)81098-3 - 21. Volman, V., Levine, H., Ben-Jacob, E. and Sejnowski, T.J. (2009) Locally Balanced Dendritic Integration by Short-Term Synaptic Plasticity and Active Dendritic Conductances. Journal of Neurophysiology, 102, 3234-3250.
http://dx.doi.org/10.1152/jn.00260.2009 - 22. Huang, E.P. and Stevens, C.F. (1997) Estimating the Distribution of Synaptic Reliabilities. Journal of Neurophysiology, 78, 2870-2880.
- 23. Zucker, R.S. and Regehr, W.G. (2002) Short-Term Synaptic Plasticity. Annual Review of Physiology, 64, 355-405.
http://dx.doi.org/10.1146/annurev.physiol.64.092501.114547 - 24. Maass, W. and Zador, A.M. (1999) Dynamic Stochastic Synapses as Computational Units. Neural Computation, 11, 903-917.
http://dx.doi.org/10.1162/089976699300016494 - 25. Matveev, V. and Wang, X.J. (2000) Differential Short-Term Synaptic Plasticity and Transmission of Complex Spike Trains: To Depress or to Facilitate? Cerebral Cortex, 10, 1143-1153.
http://dx.doi.org/10.1093/cercor/10.11.1143 - 26. Hanse, E. and Gustafsson, B. (2001) Quantal Variability at Glutamatergic Synapses in Area CA1 of the Rat Neonatal Hippocampus. Journal of Physiology, 531, 467-480.
http://dx.doi.org/10.1111/j.1469-7793.2001.0467i.x - 27. Chen, G., Harata, N.C. and Tsien, R.W. (2004) Paired-Pulse Depression of Unitary Quantal Amplitude at Single Hippocampal Synapses. Proceedings of the National Academy of Sciences of the USA, 101, 1063-1068.
http://dx.doi.org/10.1073/pnas.0307149101 - 28. Hanse, E. and Gustafsson, B. (2001) Factors Explaining Heterogeneity in Short-Term Synaptic Dynamics of Hippocampal Glutamatergic Synapses in the Neonatal Rat. Journal of Physiology, 537, 141-149.
http://dx.doi.org/10.1111/j.1469-7793.2001.0141k.x - 29. Dittman, J.S., Kreitzer, A.C. and Regehr, W.G. (2000) Interplay between Facilitation, Depression, and Residual Calcium at Three Presynaptic Terminals. Journal of Neuroscience, 20, 1374-1385.
- 30. Sun, H.Y., Lyons, S.A. and Dobrunz, L.E. (2005) Mechanisms of Target-Cell Specific Short-Term Plasticity at Schaffer Collateral Synapses onto Interneurones versus Pyramidal Cells in Juvenile Rats. Journal of Physiology, 568, 815-840.
http://dx.doi.org/10.1113/jphysiol.2005.093948 - 31. Matveev, V. and Wang, X.J. (2000) Implications of All-or-None Synaptic Transmission and Short-Term Depression beyond Vesicle Depletion: A Computational Study. Journal of Neuroscience, 20, 1575-1588.
- 32. Dobrunz, L.E. and Stevens, C.F. (1999) Response of Hippocampal Synapses to Natural Stimulation Patterns. Neuron, 22, 157-166.
http://dx.doi.org/10.1016/S0896-6273(00)80687-X - 33. Klyachko, V.A. and Stevens, C.F. (2006) Temperature-Dependent Shift of Balance among the Components of Short-Term Plasticity in Hippocampal Synapses. Journal of Neuroscience, 26, 6945-6957.
http://dx.doi.org/10.1523/JNEUROSCI.1382-06.2006 - 34. Markram, H., Wang, Y. and Tsodyks, M. (1998) Differential Signaling via the Same Axon of Neocortical Pyramidal Neurons. Proceedings of the National Academy of Sciences of the USA, 95, 5323-5328.
http://dx.doi.org/10.1073/pnas.95.9.5323 - 35. Gandhi, S.P. and Stevens, C.F. (2003) Three Modes of Synaptic Vesicular Recycling Revealed by Single-Vesicle Imaging. Nature, 423, 607-613.
http://dx.doi.org/10.1038/nature01677 - 36. Murthy, V.N., Sejnowski, T.J. and Stevens, C.F. (1997) Heterogeneous Release Properties of Visualized Individual Hippocampal Synapses. Neuron, 18, 599-612.
http://dx.doi.org/10.1016/S0896-6273(00)80301-3 - 37. Destexhe, A., Mainen, Z.F. and Sejnowski, T.J. (1996) Kinetic Models of Synaptic Transmission. In: Koch, C., Segev, I., Eds., Methods in Neuronal Modeling, MIT Press, Cambridge.
- 38. Wilson, M.A. and McNaughton, B.L. (1993) Dynamics of the Hippocampal Ensemble Code for Space. Science, 261, 1055-1058.
http://dx.doi.org/10.1126/science.8351520 - 39. Destexhe, A., Rudolph, M., Fellous, J.M. and Sejnowski, T.J. (2001) Fluctuating Synaptic Conductances Recreate in Vivo-Like Activity in Neocortical Neurons. Neuroscience, 107, 13-24.
http://dx.doi.org/10.1016/S0306-4522(01)00344-X - 40. Fellous, J.M., Rudolph, M., Destexhe, A. and Sejnowski, T.J. (2003) Synaptic Background Noise Controls the Input/Output Characteristics of Single Cells in an in Vitro Model of in Vivo Activity. Neuroscience, 122, 811-829.
http://dx.doi.org/10.1016/j.neuroscience.2003.08.027 - 41. Leutgeb, S., Leutgeb, J.K., Treves, A., Moser, M.B. and Moser. E.I. (2004) Distinct Ensemble Codes in Hippocampal Areas CA3 and CA1. Science, 305, 1295-1298.
http://dx.doi.org/10.1126/science.1100265 - 42. Colgin, L.L., Moser, E.I. and Moser, M.B. (2008) Understanding Memory through Hippocampal Remapping. Trends in Neurosciences, 31, 469-477.
http://dx.doi.org/10.1016/j.tins.2008.06.008 - 43. Leutgeb, S., Leutgeb, J.K., Moser, E.I. and Moser, M.B. (2006) Fast Rate Coding in Hippocampal CA3 Cell Ensembles. Hippocampus, 16, 765-774.
http://dx.doi.org/10.1002/hipo.20201 - 44. Fenton, A.A. and Muller, R.U. (1998) Place Cell Discharge Is Extremely Variable during Individual Passes of the Rat through the Firing Field. Proceedings of the National Academy of Sciences of the USA, 95, 3182-3187.
http://dx.doi.org/10.1073/pnas.95.6.3182 - 45. Thomson, A.M. (2000) Molecular Frequency Filters at Central Synapses. Progress in Neurobiology, 62, 159-196.
http://dx.doi.org/10.1016/S0301-0082(00)00008-3 - 46. Abbott, L.F., Varela, J.A., Sen, K. and Nelson, S.B. (1997) Synaptic Depression and Cortical Gain Control. Science, 275, 220-224.
http://dx.doi.org/10.1126/science.275.5297.221 - 47. Rothman, J.S., Cathala, L., Steuber, V. and Silver, R.A. (2009) Synaptic Depression Enables Neuronal Gain Control. Nature, 457, 1015-1018.
http://dx.doi.org/10.1038/nature07604 - 48. Manor, Y. and Nadim, F. (2001) Synaptic Depression Mediates Bistability in Neuronal Networks with Recurrent Inhibitory Connectivity. Journal of Neuroscience, 21, 9460-9470.
- 49. Markram, H., Pikus, D., Gupta, A. and Tsodyks, M. (1998) Potential for Multiple Mechanisms, Phenomena and Algorithms for Synaptic Plasticity at Single Synapses. Neuropharmacology, 37, 489-500.
http://dx.doi.org/10.1016/S0028-3908(98)00049-5 - 50. Goldman, M.S. (2004) Enhancement of Information Transmission Efficiency by Synaptic Failures. Neural Computation, 16, 1137-1162.
http://dx.doi.org/10.1162/089976604773717568 - 51. Goldman, M.S., Maldonado, P. and Abbott, L.F. (2002) Redundancy Reduction and Sustained Firing with Stochastic Depressing Synapses. Journal of Neuroscience, 22, 584-591.
Appendix
http://amygdala.psychdept.arizona.edu/Publications.html
NOTES

*Corresponding author.






