Received 9 July 2014; revised 26 August 2014; accepted 10 September 2014

ABSTRACT

β-turn is one of the most important reverse turns because of its role in protein folding. Many com- putational methods have been studied for predicting β-turns and β-turn types. However, due to the imbalanced dataset, the performance is still inadequate. In this study, we proposed a novel over-sampling technique FOST to deal with the class-imbalance problem. Experimental results on three standard benchmark datasets showed that our method is comparable with state-of-the-art methods. In addition, we applied our algorithm to five benchmark datasets from UCI Machine Learning Repository and achieved significant improvement in G-mean and Sensitivity. It means that our method is also effective for various imbalanced data other than β-turns and β-turn types.

Keywords:

Beta-Turns, Beta-Turn Types, Class-Imbalance, Over-Sampling

1. Introduction

Secondary structure that includes regular and irregular patterns is important in protein folding study because it can be a building block of three-dimensional structures. The regular structures, which are sequences of residues with repeating φ and ψ values, are classified in α-helix and β-strand. While this group is well defined, the irregular structures that cover 50% of remaining protein residues are classified as coils. In fact, coils can be tight turns, bulges, or random coils. Among them, tight turn is the most important one from the viewpoint of protein structure as well as function [1] . Tight turns are categorized as δ-, γ-, β-, α-, and π-turns according to the number of consecutive residues in the turn.

β-turn is one of the most common tight turns. It is composed of four consecutive residues that are not in an α-helix and the distance between the first and the fourth C_α is less than 7 Å [1] . β-turns play an important role in the conformation as well as the function of protein, and make up around 25% of the protein residues. β-turns are the essential part of β-hairpins, provide the directional change of the polypeptide [2] , and take part in the molecular recognition processes [3] . In addition, the formation of β-turn is a vital step in protein folding [4] . Therefore, the knowledge of β-turn is necessary in the three-dimensional structure prediction of a given primary protein sequence.

In addition, β-turns are further classified into some types according to the difference in three-dimensional structures. Based on the dihedral angles of the second and third residues in a β-turn, Hutchinson and Thornton proposed nine types of β-turn: I, I’, II, II’, IV, VIa1, VIa2, VIb, and VIII [5] . Because the types VIa1, VIa2, and VIb are rare, they are often combined into one type and named VI [1] .

Prediction of β-turn by machine learning techniques have been studied actively, for instance, by Artificial Neural Network (ANN) [6] - [8] , Support Vector Machines (SVMs) [3] [9] - [14] , logistic regression [14] [15] , and so on. In the realm of β-turn types prediction, most methods are based on ANN [6] [16] , probabilities with multiple sequence alignments as COUDES [17] , or SVMs [9] [18] [19] . However, the quality of β-turns and β-turn types prediction is still inadequate. One of the reasons is the small proportion of β-turn-residues in protein sequence. This is so-called the class-imbalance problem and often appears in Bioinformatics. The class-imbalance problem, in the serious case, causes the undesirable result that only majority class is correctly predicted.

Among many methods to handle the class-imbalance problem, resampling-based techniques including under- sampling and over-sampling methods are said to improve the classification performance significantly [20] . In this study, we propose a novel over-sampling method to deal with the class-imbalance problem in predicting β-turns and their types. Our algorithm generates the synthetic samples flexibly, for samples with minority samples as nearest neighbors as well as samples surrounded by majority samples. In addition, the new samples are informative and synthesized in a safe area. We present the experimental results on three standard benchmark datasets compared with state-of-the-art β-turns and β-turn types prediction methods. We also evaluate the performance of the novel over-sampling algorithm on the five other datasets from UCI Machine Learning Repository.

2. Materials and Methods

2.1. Datasets

We chose a benchmark dataset BT426 for the performance evaluation of our β-turn prediction method. It has been used in many researches [3] [6] - [10] [12] [13] [15] as the standard dataset for the comparison. In addition, two more other datasets, BT547and BT823, that were constructed for training and testing COUDES [17] , were also used in our study. These datasets contain 426,547 and 823 protein sequences, respectively. All these protein chains have at least one β-turn and the similarity of each pair of chains is less than 25%. The observed turns and turn types in protein sequences were assigned by PROMOTIF program [21] . Table 1 presents the ratio of residues belonging to β-turn or β-turn type i to the non-β-turn or non-β-turn type i (i = I, I’, II, II’, IV, VI, VIII) in these datasets.

2.2. Features

In this work, PSSMs (Position Specific Scoring Matrices), predicted shape strings, and predicted protein blocks

were used as the input features to predict β-turns and their types.

2.2.1. PSSMs

PSSMs were generated by using PSI-BLAST [22] against National Center for Biotechnology Information (NCBI) non-redundant sequence database with default parameters. PSSM is a matrix of N rows corresponding to the length of the protein sequence and 20 columns corresponding to 20 kinds of standard amino acids.

2.2.2. Predicted Shape Strings

Each residue in a protein sequence can be categorized into one of eight groups that are symbolized by eight symbols (S, R, U, V, K, A, T, and G) according to the phi-psi torsion angles. A sequence of these symbols makes up a shape string of a corresponding protein. The authors in [14] [23] used predicted shape strings to enhance the beta-turn prediction result.

In this work, DSP program [24] was used to predict the shape strings. Besides the eight states above, N is used to represent the residue with undefined phi-psi angles. Each state was encoded as a vector of nine features (1,0,0,0,0,0,0,0,0) for S, (0,1,0,0,0,0,0,0,0) for R, and so on.

2.2.3. Predicted Protein Blocks

Though predicted secondary structures of protein were effective in predicting β-turns and their types [7] [9] [12] [14] [23] , the way of classifying a secondary structure of protein into three states of backbone conformation as α-helix, β-sheet, and coil leads to the circumstance that 50% total number residues are assigned as coils while they are believed to belong to a large set of distinct local structures [25] [26] . Therefore, the structural alphabets (SAs), that are sets of specific prototypes approximating the local protein structure, were developed to overcome this drawback [25] .

Protein blocks, that allow a good approximation of local protein 3D structures [27] [28] , have been utilized in many applications [26] [29] . SAs for protein blocks are sixteen pentapeptide motifs with labels A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, and P. Each of these prototypes represents a vector of eight average phi-psi angles.

In this research, predicted protein blocks were obtained from the website of PB-kPRED (http://www.bo-protscience.fr/pentapept/?page_id=9). Sixteen characters from A to P symbolize sixteen corresponding blocks and X for the other state. For each residue i in a protein chain, the corresponding predicted protein block was represented by a vector of seventeen features, where 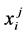was the probability of residue i as state j.

The feature vector of each query residue was generated by using a sliding window of size nine amino acids. Thus, one input vector contained 414 attributes, where each PSSM value x was scaled to the range by the logistic function:

(1)

and the other values were normalized.

2.3. Methods

2.3.1. Resampling Techniques

Resampling techniques are said to effectively improve classification accuracy of the imbalanced datasets. While under-sampling methods decrease the number of majority samples, over-sampling methods enlarge the number of minority samples to rebalance the imbalanced dataset. However, the removal of samples may cause the significant information loss for the majority class. This is the main drawback of under-sampling methods. In contrast, over-sampling methods synthesize new minority samples in various ways. The most naïve method is random over-sampling that randomly chooses and replicates some minority samples. This method is simple, but often results in over-fitting. Another well-known over-sampling method is SMOTE [30] , which generates the new samples by using the information of each minority sample and its randomly chosen minority nearest neighbor. The synthetic minority samples are located between these two minority samples considered. Therefore, SMOTE can improve the quality of synthetic samples; however, it may lead to the overlapping in classes. This problem becomes more serious when the original imbalanced dataset contains many isolated minority samples, which are the samples surrounded by the majority samples. To alleviate both problems of over lapping and over-fitting, we propose a novel over-sampling method named Flexible Over-Sampling Technique (FOST).

2.3.2. Flexible Over-Sampling Technique

The main idea of FOST is to improve the density of each minority sample flexibly depending on the number of its nearest neighbors which belong to minority class. First of all, as shown in the pseudo-code below, FOST finds k nearest neighbors for each minority sample x (line 3). Note that the k nearest neighbors here can be minority samples, majority samples, or synthetic samples generated by the function Self_sample_generation (line 6) or Sample_generation (line 12). FOST synthesizes the new samples for x as follows:

· If 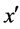is the nearest neighbor of x and and belongs to the majority class (line 5), FOST generates d synthetic samples opposite to 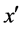so that the distances from these samples to x are less than the distance between x and 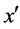(lines 16 - 22).

· If there are m (m < k) minority nearest neighbors of x and the distances from these samples to x are less than the distance from 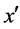to x (line 8), FOST synthesizes d new samples as follows: 1) computes the sample y that is the centroid of m minority nearest neighbors and x (line 9); 2) generates a sample between y and one randomly chosen sample among its (m + 1) nearest neighbors (lines 23 - 27).

· If all k nearest neighbors of x belong to the minority class, FOST does not generate any synthetic sample.

The pseudo-code for FOST algorithm is as follows:

2.3.3. FOST Algorithm

Input: Minority dataset M; Majority dataset N; ratio of generation d; threshold k;

Output: set of synthetic samples S;

Begin

1);

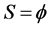2) For each;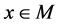

3) Find k nearest neighbors of x in;

4) If exists a majority nearest neighbor 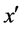among these k nearest neighbors of x;

5) If 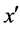is the most nearest neighbor of x;

6) Self_samples_generation;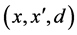

7) else;

8): m minority samples whose distances to x are smaller than the distance between x and, m < k;

9): the new minority sample where;

10) For l = 1:d;

11): is randomly chosen from;

12) Samples_generation;

13) end_for;

14) Update S;

15) End_for;

End

Function Self_samples_generation;

Input: samples;; number of new samples d;

Output: set of synthetic samples new_spls_arr of x;

Begin

16) For i = 1:d;

17) new_sample_CL = x_CL;

18) For j = 1:n;

19) new_sample_j =

20) end_for;

21) push (new_spls_arr, new_sample);

22) end_for;

End

Function Samples_generation;

Input: samples;;

Output: set of synthetic samples new_spls_arr of x;

Begin

23) new_sample_CL=x_CL;

24) for j = 1:n;

25) new_sample_j =

26) end_for;

27) push (new_spls_arr, new_sample);

End

2.3.4. Performance Evaluation of the Method

Since the ratio of β-turn to non-β-turn samples is around 1:3, the datasets are imbalanced. Support Vector Machine (SVM) was used as the basis classifier in this study since it is said to be better than other standard classifiers in dealing with imbalanced dataset. Specifically, ksvm function in kernlab package for R software [31] with Gaussian RBF kernel was employed.

We conducted seven-fold cross validation to evaluate the performance of our method. Each dataset was divided into seven parts that contained the same number of positive samples. Then, the feature selection based on information gain ratio [32] was applied to reduce the redundant features and achieve the highest MCC. After that, FOST was used to relax the imbalance ratio of the datasets. We set the threshold k = 10 for every case. The ratio of over-sampling d was chosen via grid search in each case.

To predict β-turn types, we created the same architecture as the prediction of β-turns, except the goal of the prediction was the β-turn type i (i = I, I’, II, II’, IV). It means that the non-β-turn residues and the residues belonging to β-turn type j, , were the negative samples. In the cases of type VI and VIII, due to the high imbalance ratio, we random-under-sampled to relax the imbalance ratio before applying feature selection and FOST.

Since a β-turn contains at least four consecutive residues, the output needed to be filtered by applying the following rules in order [6] :

1) Change isolated predicted non-turn to turn: tnt → ttt.

2) Change isolated predicted turn to non-turn: ntn → nnn.

3) Change the two non-turn neighbors of two successive turns to turns: nttn → tttt.

4) Change the two non-turn neighbors of three successive turns to turns: ntttn → ttttt.

These rules ensure that the length of every final predicted turn is at least four residues.

Figure 1 demonstrates the overall architecture of our prediction method.

2.3.5. Performance Metrics

As MCC, Q_total, Q_observed, Q_predicted are often used to measure the quality of β-turn prediction methods [17] , they are used to evaluate the performance of our method and are defined as below:

(2)

(3)

(4)

(5)

where TP, TN, FP, FN are the number of true positive, true negative, false positive and false negative samples, respectively.

MCC, which lies in is used to evaluate the correlation of the predicted and the observed class labels. Three values of −1, 0, 1 correspond to the worst, the random and the best predictor, respectively. It is the most robust measure for β-turn prediction [9] .

In addition, the threshold-independent measures ROC (Receiver Operating Characteristics) and AUC (Area Under the Curve), which are often used in bioinformatics [33] , are adopted.

3. Results and Discussions

3.1. Prediction of Turn/Non-Turn

The proper choice of sliding window size for extracting the feature vectors affects the performance of prediction. Shepherd [6] showed that window of seven or nine residues was optimal for β-turn prediction. In the experiments, we tested various sliding window sizes and selected the size of nine residues since it returns not only the highest MCC but also the highest Q_total, Q_observed, and Q_predicted.

We also performed experiments to evaluate the impact of evolutionary information PSSMs, predicted protein blocks, and predicted shape string combinations. Table 2 presents the effect of these feature groups on the BT426 dataset in predicting β-turn. The results show that using all three groups of features achieved the highest MCC, Q_total, Q_observed, Q_predicted, and AUC in comparison to using two of three of them. The highest performance results of the existing method that used PSSMs and predicted secondary structure as input features are 82.87%, 70.66%, 64.83%, 0.56, and 0.886 on Q_total, Q_observed, Q_predicted, MCC, and AUC, respectively [14] . In the case of using PSSMs and predicted protein blocks as input features, we achieved higher Q_total, Q_predicted, MCC, and AUC (1.85%, 5.01%, 0.03, and 0.007, respectively). It shows that predicted protein blocks are useful in identifying β-turns.

Figure 2 presents the ROC curves for predicting β-turn using the different combinations of feature groups on the BT426 dataset.

Our method outperformed the other competing methods with MCC of 0.66 except Tang et al. and H-SVM-LR. In comparison to Tang et al., though MCC of the both methods was 0.66, we attained higher Q_total (87.48% vs. 87.2%) and Q_predicted (75.26% vs. 73.8%). H-SVM-LR achieved higher MCC than us (0.01), but lower Q_total and Q_predicted (87.37% vs. 87.48% and 74.99% vs. 75.26%, respectively). Note that while we applied the filtering to make the predicted beta-turn more realistic, H-SVM-LR did not. Table 3 shows the results of all methods in detail.

Table 2 and Table 3 show that the use of feature selection for eliminating redundant features and FOST to relax the class-imbalance, not only increase Q_total (0.9%), Q_predicted (3.81%) but also MCC (0.02).

Figure 3 displays the ROC curve of our method, with the AUC was 0.921.

Besides the BT426 dataset, we performed the experiments on two more additional datasets, BT547 and BT823. Table 4 presents the results of our method on the datasets BT547 and BT823 with MCCs of 0.66 and 0.67, respectively. The ROC curves of these two datasets are shown in Figure 4.

3.2. Prediction of β-Turn Types

The performance of our method in predicting β-turn types on the three datasets BT426, BT547, and BT823 is shown in Table 5. All the AUC values are higher than 0.7, and most of them are higher than 0.85. It proves our method is acceptable in predicting β-turn types [15] .

Table 6 presents the MCCs of the competing methods. Only our method could predict type VI. While DEBT could not predict types I’ and II’, our method achieved the highest MCC in comparison with other methods on all three datasets (0.75 and 0.64 on BT426; 0.78 and 0.66 on BT547; 0.80 and 0.66 on BT823 for type I’ and II’, respectively). Our method also achieved the highest MCC in predicting type II and VIII (0.75 and 0.30 on BT426; 0.77 and 0.35 on BT547; 0.77 and 0.33 on BT823). For type I, our method resulted in lower MCC in comparison to Shi et al. on BT426 (0.61 vs. 0.71), and equally on BT823 (0.64), but higher on BT547 (0.63 vs. 0.53). In the case of type IV, Shi et al. was the winner on BT426 (0.46), but our method achieved the best MCCs on BT547 (0.40) and BT823 (0.40). ROC curves of our β-turn types prediction are shown in Figure 5.

3.3. Datasets from UCI Machine Learning Repository

In addition to three standard benchmark datasets above, we evaluated the performance of our novel over-sam- pling algorithm FOST on the five datasets which were obtained from UCI Machine Learning Repository [34] : Haberman’s Survival, Pima Indian Diabetes, Glass Identification, Landsat Satellite, and Yeast. The details of these datasets are described in Table 7.

The experiments were implemented to compare our method with the control method (i.e. no over-sampling) and SMOTE, using ksvm as the classifier with Gaussian RBF kernel and default parameters. We conducted the 10 independent times of 10-fold cross-validation on every dataset and averaged to get the performance of the methods. The optimal number of synthetic samples of each dataset for FOST algorithm was decided by grid

search, and then applied for SMOTE. Table 8 presents the Accuracy, Sensitivity, Specificity, and G-mean of the

competing methods. Specificity and G-mean are defined as follows:

(6)

(7)

We also performed the two-sample t-test with equal variance to assess if the average G-means of different methods are significantly different. Table 9 presents the p-values of these t-test comparisons between each pair of corresponding methods. All the p-values are smaller than 0.05, it means that our method achieves the better G-mean on all five benchmark datasets.

4. Conclusion

In this study, we presented a new method to identify β-turns and β-turn types in protein sequences. We showed that the use of predicted protein blocks as the input features well affected the prediction results. We also proposed a novel over-sampling algorithm FOST to relax the class-imbalance for the β-turn datasets effectively and improve the prediction performance. The combination of our new algorithm and the protein blocks features led to the significant improvement in prediction of β-turn types, especially, could predict type VI which is often

ignored by the previous methods. The experimental results on the UCI Machine Learning Repository datasets showed that FOST achieved better G-mean and Sensitivity than the control method and SMOTE with p-values less than 0.05. It means that our method is also effective for various imbalanced data other than β-turns and β-turn types.

Acknowledgements

In this research, the super-computing resource was provided by Human Genome Center, the Institute of Medical Science, The University of Tokyo. Additional computation time was provided by the super computer system in Research Organization of Information and Systems (ROIS), National Institute of Genetics (NIG). The authors also wish to thank Dr. Osamu Hirose, Graduate School of Natural Science and Technology, Kanazawa University, Japan for his valuable comments.

References