Journal of Biomedical Science and Engineering
Vol.7 No.4(2014), Article ID:43758,10 pages DOI:10.4236/jbise.2014.74024
ANFIS-PID Control FES-Supported Sit-to-Stand in Paraplegics: (Simulation Study)
Rufaida Hussain, Rasha Massoud, Moustafa Al-Mawaldi
Department of Biomedical Engineering, Electrical and Mechanical Engineering Faculty, Damascus University, Damascus, Syria
Email: rufaidahussain@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 16 January 2014; revised 20 February 2014; accepted 28 February 2014
ABSTRACT
Adaptive Neuro-fuzzy Inference System (ANFIS) controller was designed to control knee joint during sit to stand movement through electrical stimuli to quadriceps muscles. The developed ANFIS works as an inverse model to the system (functional electrical stimulation (FES)-induced quadriceps-lower leg system), while there is a proportional-integral-derivative (PID) controller in the feedback control. They were designated as ANFIS-PID controller. To evaluate the ANFIS-PID controller, two controllers were developed: open loop and feedback controllers. The results showed that ANFIS-PID controller not only succeeded in controlling knee joint motion during sit to stand movement, but also reduced the deviations between desired trajectory and actual knee movement to ±5˚. Promising simulation results provide the potential for feasible clinical application in the future.
Keywords:Adaptive Neuro-Fuzzy Inference System (ANFIS); Functional Electrical Stimulation (FES); Sit to Stand; Model; Simulation

1. Introduction
Sit to stand movement is necessary for many activities in human life. However, paraplegics have particular difficulty with this movement due to their lower limb paralysis caused by spinal cord injury (SCI) [1] . They consider it as a big challenge and often require an assistant [2] . Moreover, they use arm support to provide necessary forces during standing-up. Consequently, people practicing a fully arm supported standing-up face later shoulder complications [3] .
In addition to arm support, paraplegics can use functional electrical stimulation (FES). It is a promising technology that can facilitate sit to stand in paraplegia [4] [5] . It adjusts artificial electrical stimulation pulses to induce muscle contraction and the corresponding joint movement.
Achieving desired movement requires suitable electrical stimulation currents to the muscles [6] , but the control of multiple joints’ movement is difficult due to its complexity, non-linearity, and time-variance of the human body movement involved. Furthermore, physiological effects such as: muscle fatigue, spasticity, and limited force in the stimulated muscle are difficult to be modeled and controlled [7] .
The solution of FES control problems requires intelligent systems that emulate the way how human brain controls the muscles. Researchers used artificial neural network [8] and fuzzy logic [9] [10] to control different kinds of human movement like free swing legs, walking, and sit to stand in simulations in general and some rear studies in clinical laboratories. These techniques are quite different from conventional, and yet with unique capabilities in: specifying mathematical relationships in a complex system, performing mappings with degree of imprecision, and controlling of nonlinear system [4] . Simulation results indicated that it was feasible to provide significant improvements to the FES control sit to stand [8] -[10] . However, according to the results of studies [9] [10] , the fuzzy controllers not only required a lot of simulation trials for manual tuning but also applied high moments in knee joints during sit to stand movement. While the results of neural networks controllers affected by chance effects, over training and interpretation, until now neither fuzzy logic nor neural network controllers have put on the market.
To overcome the drawbacks of neural networks and fuzzy logic, Adaptive Neuro-Fuzzy Inference System (ANFIS) was successfully applied to robotic motion and controlling free leg swing during electrical stimuli to quadriceps muscles. The present study aims to develop an adaptive intelligent controller which calculates the required stimulus activation of quadricep muscles to assess the paraplegic sit to stand. It depends on ANFIS which is combining the adaptive learning capability of artificial neural network with the intuitive fuzzy logic of human reasoning formulated.
2. Methods
Figure 1 illustrates the block diagram of the control system. This system consists of two elements: an ANFIS controller and a fixed parameter proportional-integral-derivative (PID) controller, which designates the ANFISPID controller. The plant represents the humanoid model (quadriceps lower leg system). Once the ANFIS is successfully trained to mimic the inverse dynamics of the plant, it could calculate the required stimulus activation of the quadriceps muscle using the desired motion trajectories. However, some degree of modeling error is unavoidable, since modeling could never perfectly represent physiological musculoskeletal systems. Therefore, a PID feedback controller in parallel is incorporated into the design of the ANFIS control system to compensate for the residual tracking errors caused by the disturbances and modeling errors. This study uses three different control system configurations and compares their control performances during sit to stand movement: an ANFIS-PID controller, an ANFIS controller alone, and a PID controller.
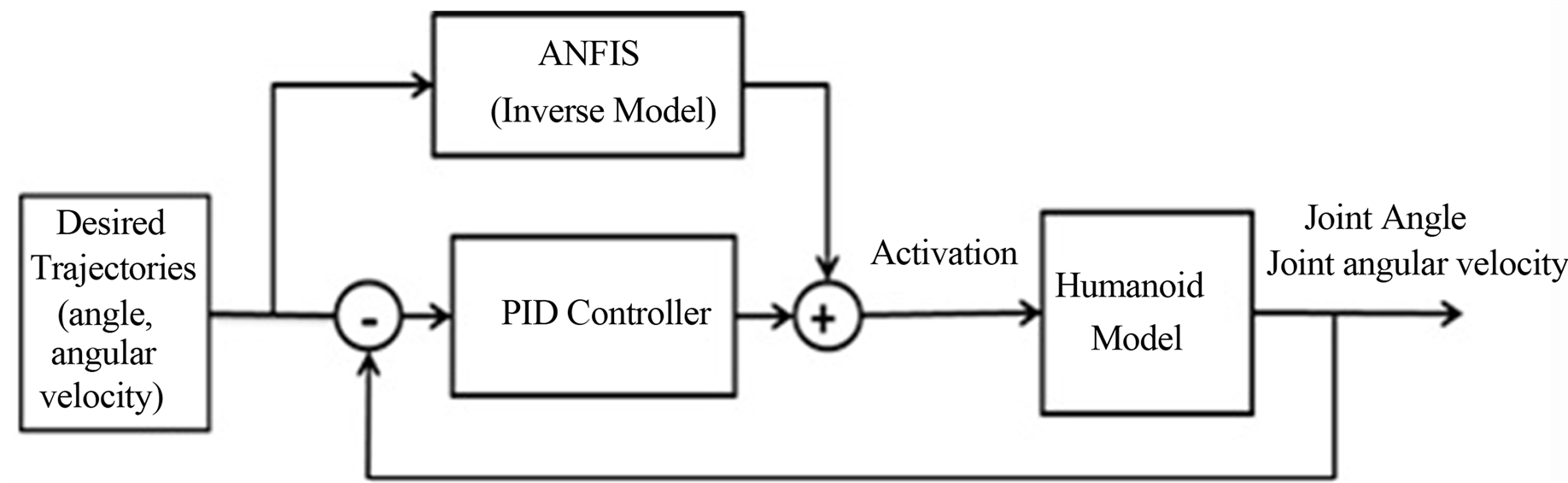
Figure 1. A block diagram of ANFIS-PID control system.
2.1. Model of the Paraplegic
Paraplegic model is essential for design FES controllers. A model for a patient height 1.80 m and weight 75.35 Kg was built. The model contains: body segments, muscles, and passive joint properties as is illustrated in Figure 2. The Input to the model is the activation produced by stimulator (pulse generator). The controlled variable is the Stimulation amplitude which ranged from 0 to 300 mA with fixed pulse width (250 µs) while the pulse frequencies fixed to 20 Hz. Model output is the knee angular trajectory as resulting from a given set of stimulation patterns delivered to the muscle group.
The body segments model was developed using Visual Nastran which is a powerful CAD tool used for 3-D modeling [11] . The human body segments were described by a simple geometrical model consisting of: feet, shanks, thighs, upper arms, forearms, hands, and trunk-neck -head. The body segments physical parameters were scaled to body mass and height according to Winter [12] . The body segments were connected by joints: one neck, two shoulders, two elbows, two wrists, two hips, two knees and two ankles. All joints are set to have only one degree of freedom (DOF) except for neck. Since the project is focused on sit to stand movement without upper body support, the most important joints are hips, knee and ankle, while the shoulders, elbows and wrists are considered as passive.
Quadriceps muscles group (which consists of four muscles: Rectus Femoris, Vastusmedialis, Vastus medium, and Vastuslateralis) was modeled in Virtual Muscle 4.0.1 by using muscles parameters from [13] . Virtual muscle builds realistic Simulink models of muscles responding to either natural recruitment or FES [14] . All modeled muscles have one activation signal as input. The active moment developed by a single muscle is calculated from its non-linear moment arm and the muscle force, which is the output of virtual muscle Simulink block [15] .
In the body-segmental dynamics, total joint moment is the sum of active, passive elastic and passive viscous joint moments. The latter has been modeled as a linear relation between the angular joint velocity and the damping coefficient [16] , while passive elastic joint moments have been modeled by double exponential equations, which account for the influence of the adjacent joint angles [16] . Active joint moment is the sum of the joint moments produced by each muscle [15] .
2.2. Adaptive Neuro-Fuzzy Inference System
The Adaptive Neuro-Fuzzy Inference System (ANFIS) technique was originally presented by Jang in 1993 [17] . It combines the benefits of the fuzzy logic and neural network systems into a single technique. An ANFIS applies neural network learning methods to tune the parameters of a Fuzzy Inference System (FIS).
ANFIS architecture consists of five layers with the output of the nodes layered architecture [17] as shown in Figure 3:
The first layer generates the membership grades.
The second generates the firing strengths by multiplying the incoming signals and outputs the t-norm operator results.
The third layers normalize the firing strengths.
The fourth layer calculates the first-order Takagi-Sugeno rules for each fuzzy rule based on the consequent parameters.
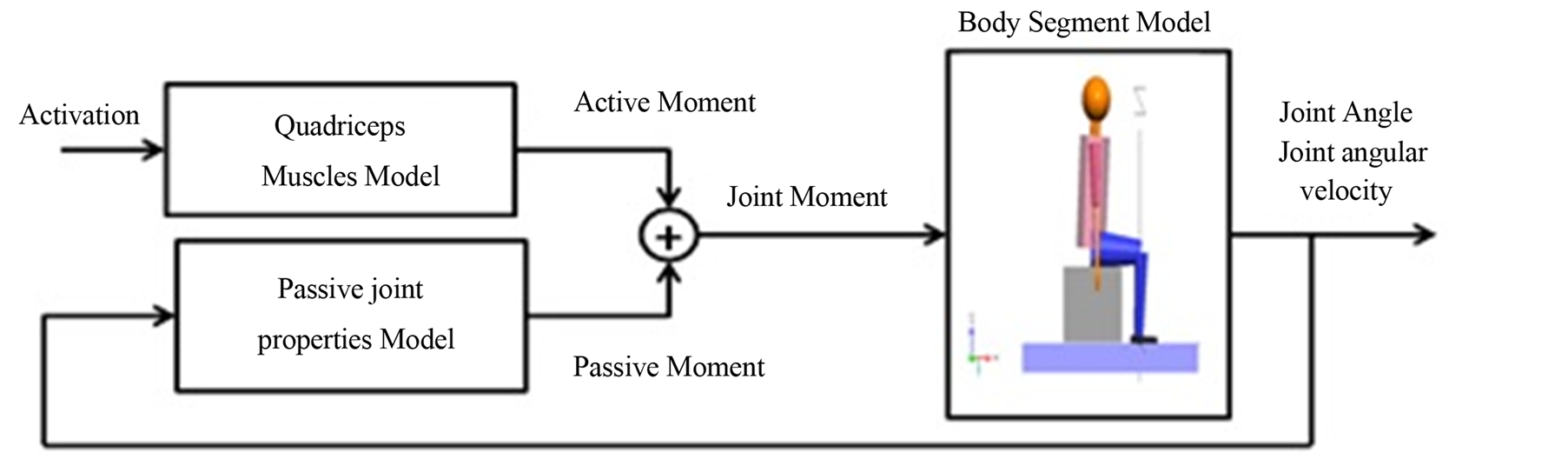
Figure 2. Paraplegic Patient model. The main parts of the model are: body segments, muscles, and passive joint properties.
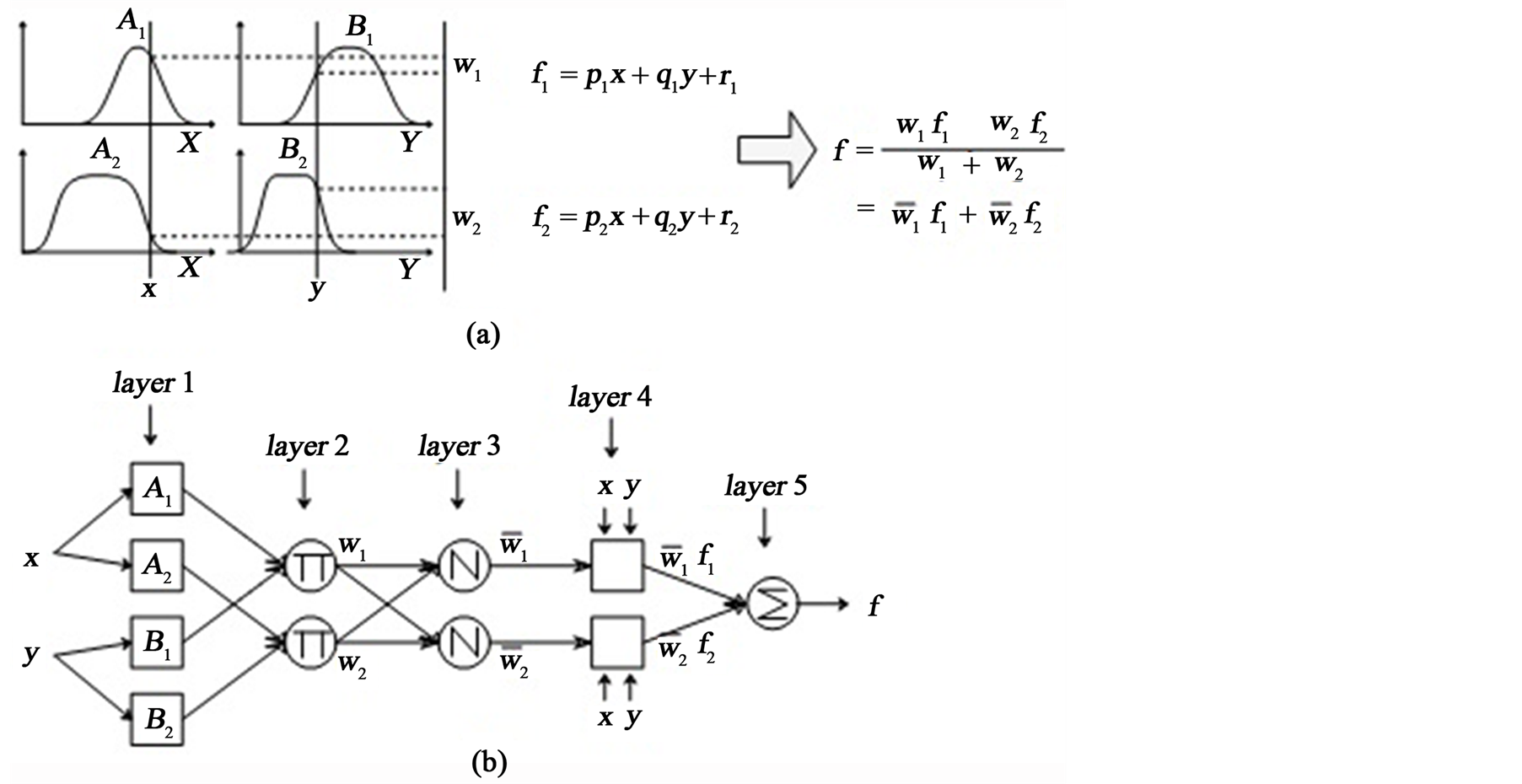
Figure 3. Two-input first-order Sugeno fuzzy model and (b) equivalent ANFIS architecture for two rules [11] .
The fifth layer—the output layer, calculates the weighted global output of the system as the summation of incoming signals [17] .
ANFIS uses back propagation learning to determine premise parameters and least mean squares estimation to determine the consequent parameters [11] . This is referred to as hybrid learning. A step in the learning procedure has got two passes:
• In the first or forward pass, the input patterns are propagated, and the optimal on consequent parameters are estimated by an iterative least mean square procedure, while the premise parameters are assumed to be fixed for the current cycle through the training set.
• In the second or backward pass the patterns are propagated again, and in this epoch, back propagation is used to modify the premise parameters, while the consequent parameters remain fixed. This procedure is then iterated until the error criterion is satisfied [11] .
2.2.1. ANFIS Based Modeling of Knee-Joint Dynamics
Figure 4 shows ANFIS architecture employed for modeling the knee-joint dynamics. The structure of ANFIS as part of Matlab’s Fuzzy Logic Toolbox has been used effectively for building a set of fuzzy if-then rules with appropriate membership functions.
ANFIS model has two inputs: knee joint angle and angular velocity, and the activation pattern as output. The implemented is based on:
• First-order Sugeno fuzzy model so the consequent part of fuzzy if-then rules is a linear equation.
• T-norms operator that performs fuzzy AND is algebraic product.
• The type of membership functions (MF) of the inputs are Gaussian functions.
• Each input has three membership functions which are chosen by trial and error, so the number of fuzzy rules is nine.
2.2.2. Training ANFIS
The ANFIS training off-line methodology using ANFIS GUI in Matlab Fuzzy Logic Toolbox is summarized in Figure 5. The process begins by obtaining a training data set (input/output data pairs). The training signals were formed by stimulating the implant model with several random and sinusoidal signals with amplitudes variable between 0 and 300 mA and recording knee joint response (knee angle and angular velocity). The training data set is used to find the premise parameters for the membership functions. A threshold value for the error between the actual and desired output is determined. The consequent parameters are found using the least squares me-
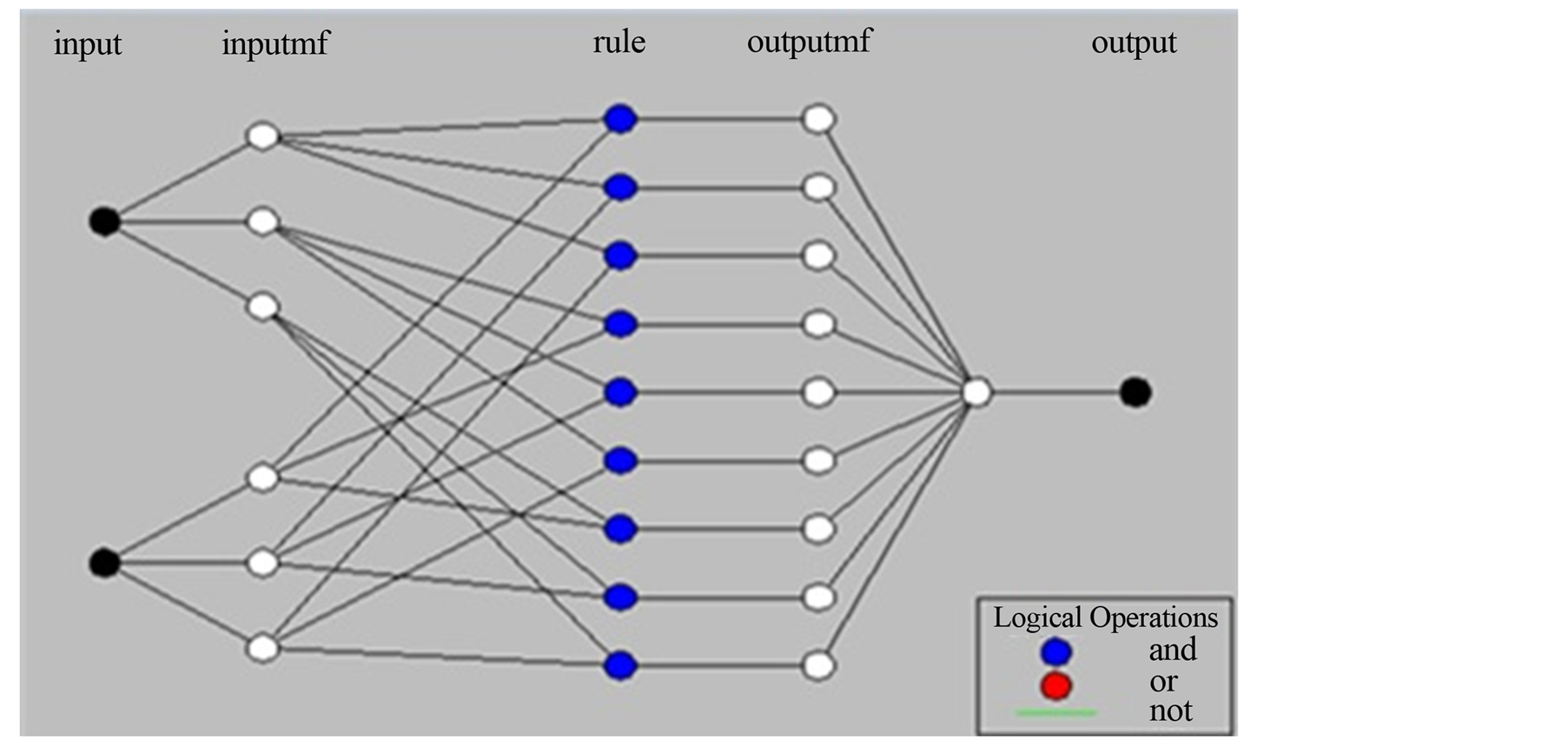
Figure 4. Structure of the proposed ANFIS model in Matlab.
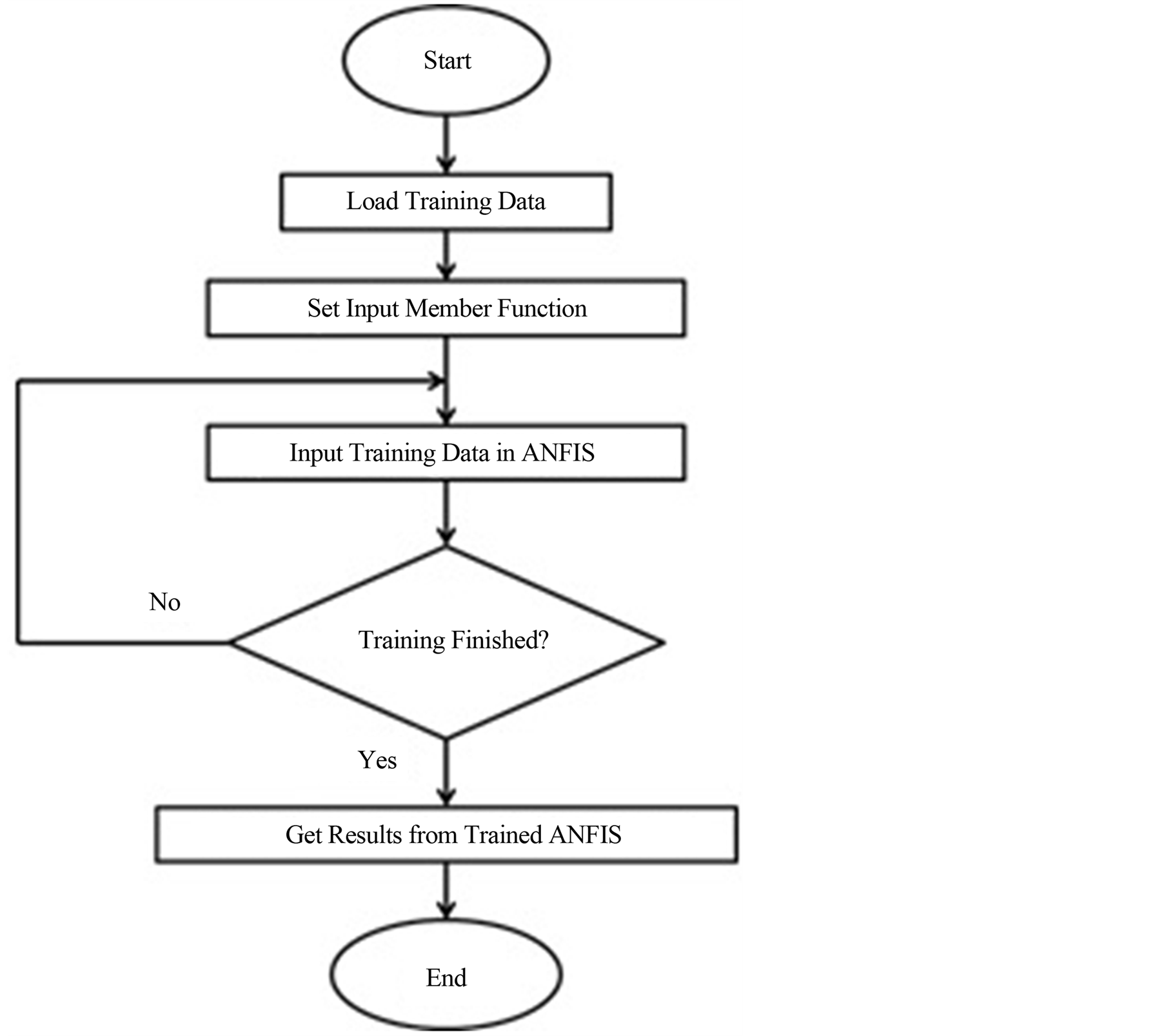
Figure 5. ANFIS training process [18].
thod. If this error is larger than the threshold value, then the premise parameters are updated using the gradient decent method (back propagation). The process is terminated when the error becomes less than the threshold value. The checking data set is then used to compare the model with the actual system [18] .
2.3. PID Controller
Proportional-integral-derivative (PID) controller may be the most widely used controller because of its simplicity and efficiency. The PID controller transfer function, F(s), is:
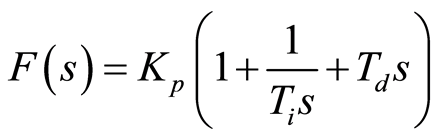 (1)
(1)
where:
KP is the proportional gain of the Controller.
KP/τi is the integral gain of the controller.
Kpτd is the differential gain of the controller.
The parameters of the PID controller were tuned using the Ziegler–Nichols’ method based on the step response of the open-loop system [19] , then they were adjusted using trial and error depending on the properties of the PID controller.
2.4. Controllers Design
Building FES controller-ANFIS-PID controller-as a tracking controller requires two steps:
1) Determine reference trajectory-the controller input-which represents the desired joint angles during sit to stand movement. This paper defined it based on [10] [16] . The desired knee joint angular trajectory was developed based on the initial position of standing-up movement while the model in seated position where the knee joint angle equals to 90˚ and the movement end when knee is in full extension and the body is in standing balance position.
2) Determine the control system configuration that makes the plant follows the desired trajectory. ANFIS-PID structure is used in this paper (Figure 6). The humanoid model in seated position is used as the plant model. The controller input is set as the kneed_ref block which generates the desired knee angular trajectory. The output of kneed_ref and its derivative are fed forward to the ANFIS model. While the differences between reference trajectory and the actual knee angles are fed to the PID controller which works as a feedback controller to compensate for model errors and/or any external or internal disturbances. Gain block is used as a signal amplifier while the saturation block is used for electrical current safety.
Then the study uses different control system configurations-ANFIS open loop controller, and a PID controller and compares their control performances during sit to stand movement to the ANFIS-PID controller
a) ANFIS open loop Controller:
The simplest approach for controller design is a completely open-loop control strategy, in which the controller is the inverse of the process. Figure 7 shows the controller as ANFIS model which is used in series with the plant.
b) PID controller:
Figure 8 shows Proportional-integral-derivative (PID) controller that the input of the PID controller is the error signal obtained from the difference between the reference trajectory and the actual trajectory. The controller is then produced the desired activation for muscles to perform the desired standing-up movement.
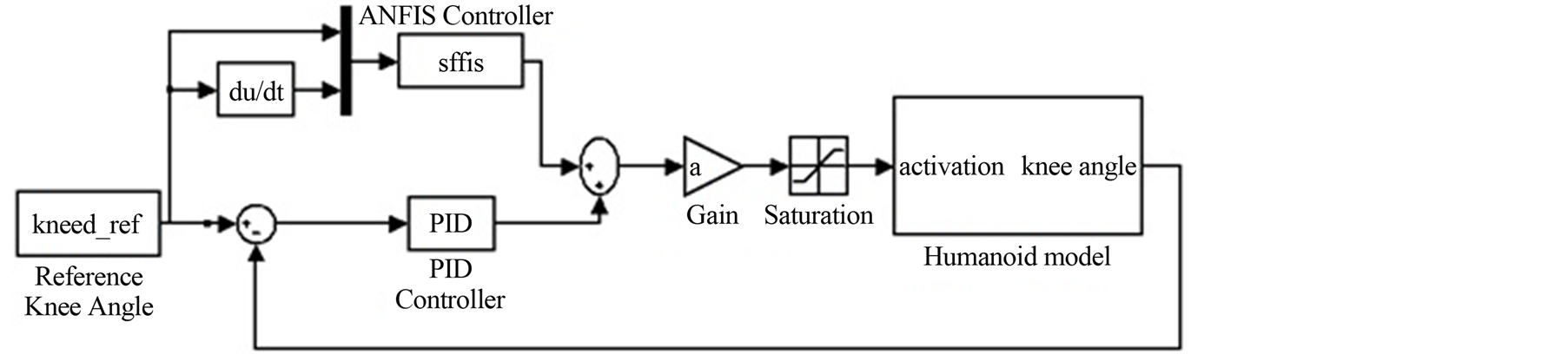
Figure 6. ANFIS-PID control system configuration.

Figure 7. ANFIS open loop control system configuration.
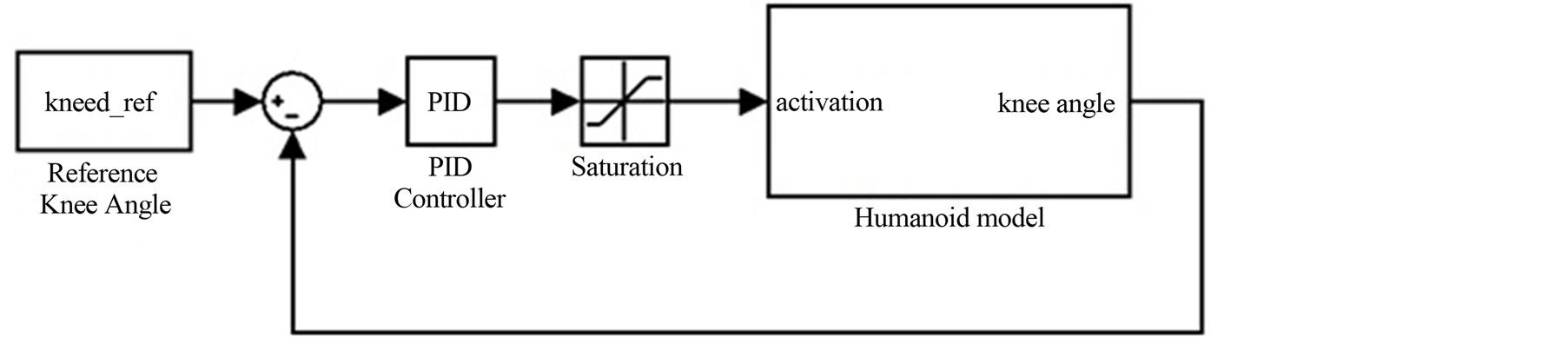
Figure 8. PID control system.
3. Results
Failing to control knee joint position during sit to stand causes a disaster accident to the body [13] , so the simulation study focused on design an ANFIS-PID control system to control knee joint position during quadriceps stimulation. The model successfully performs sit to stand activity with the three proposed controllers (PID, ANFIS open loop, ANFIS-PID controllers), where the control trajectories are tracked closely the desired trajectory and achieved full knee extension without upper body support. Figure 9 shows the simulation results of the knee joint angle control based on the PID controller, the ANFIS controller alone, and the ANFIS-PID controller for the humanoid model.
Figure 9(a) indicates that the trained ANFIS controller is capable of controlling the knee joint angle to follow the desired knee joint angle with small tracking differences. The performance of the PID controller alone is illustrates in Figure 9(b), where the knee joint trajectory poorly traced the desired trajectory. The response of position tracking by the ANFIS-PID controller is improved after combining the PID with the ANFIS controller to compensate the residual tracking errors caused by disturbances and modeling error (Figure 9(c)).
Figure 10 shows that the performances of the ANFIS open loop and the ANFIS-PID controller are significantly better than that of the PID controller. The ANFIS-PID controller demonstrates a slightly better performance than the ANFIS alone controller. Using ANFID-PID controller reduced the deviations between desired trajectory and actual knee movement trajectory-which is called tracking error-to ±0.0873 rad (the tracking error for the PID controller is ±0.2094 rad and for ANFIS alone controller is 0.1396 rad).
The moments given by controllers are varying between 0 - 104 N∙m (Figure 11). The positive moment is applied at the knee joint during initiation phase. The maximum positive torques is fired between seat unloading to quiet standing position. It’s clear from Figures 10 and 11 that both errors and knee joint moments are high, particularly during the range from 0.5 s to 1.4 seconds, because hip and knee joints have interrelated movements during this period.
4. Discussion
Simulation results confirm that ANFIS-PID improves sit to stand performance comparing with conventional control methods like open loop and PID controllers. The success of the ANFIS-PID control system in this evaluation indicates that it may provide significant improvements to existing FES control system. In comparison with other studies which use intelligent techniques such as Fuzzy logic [10] or Neural Network [8] , the results of this study show better performance regarding to minimizing errors during tracking desired motion.
According to simulation the paralysis subject model was leaning further forward at the hips and trunk during the movement to control knee angular velocity, which caused an increase in knee joint moment. If the model’s knee angular velocity can be reduced and better controlled by either stimulating hip extensors beside to quadriceps muscle group during the rising motion or damping knee flexion with an appropriately tuned Orthosis, then it should be possible to reduce the knee moment and reach smoother movement.
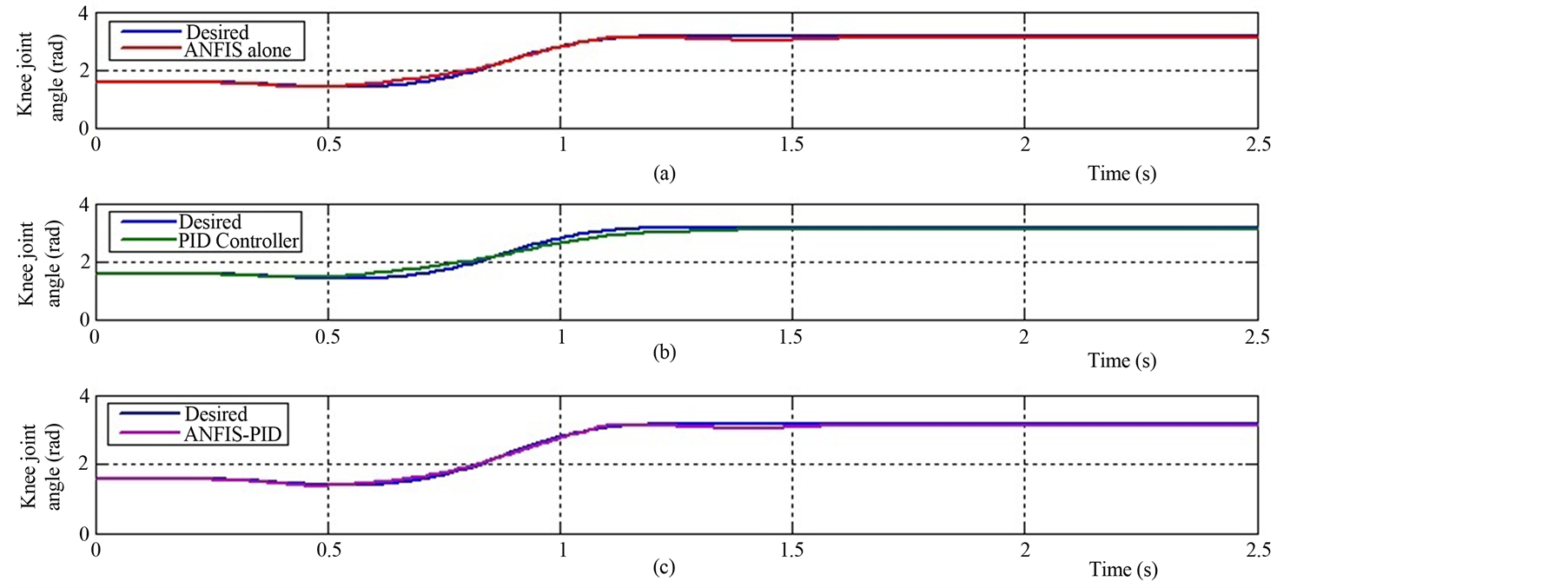
Figure 9. The simulation results of the knee joint angle control based on: (a) ANFIS controller alone; (b) the PID controller; and (c) ANFIS-PID controller for the humanoid model.
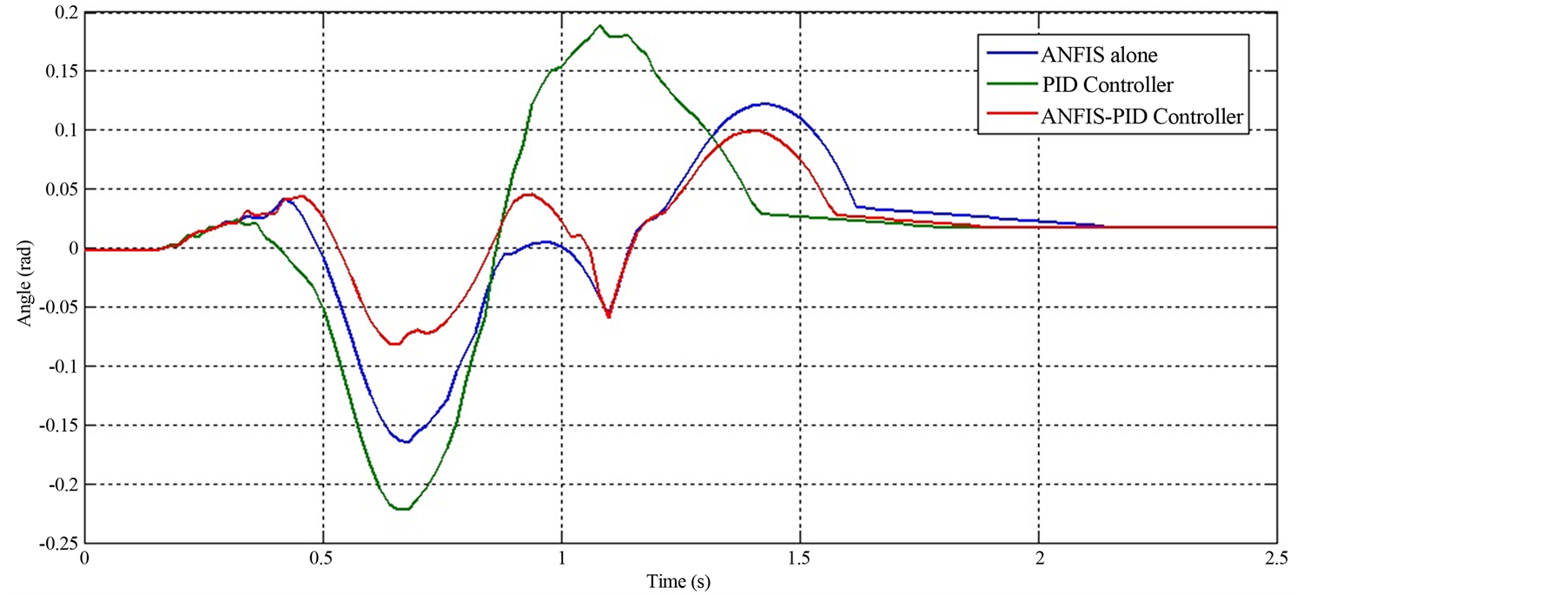
Figure 10. The tracking errors between desired trajectory and actual knee movement trajectory for three types of controllers.
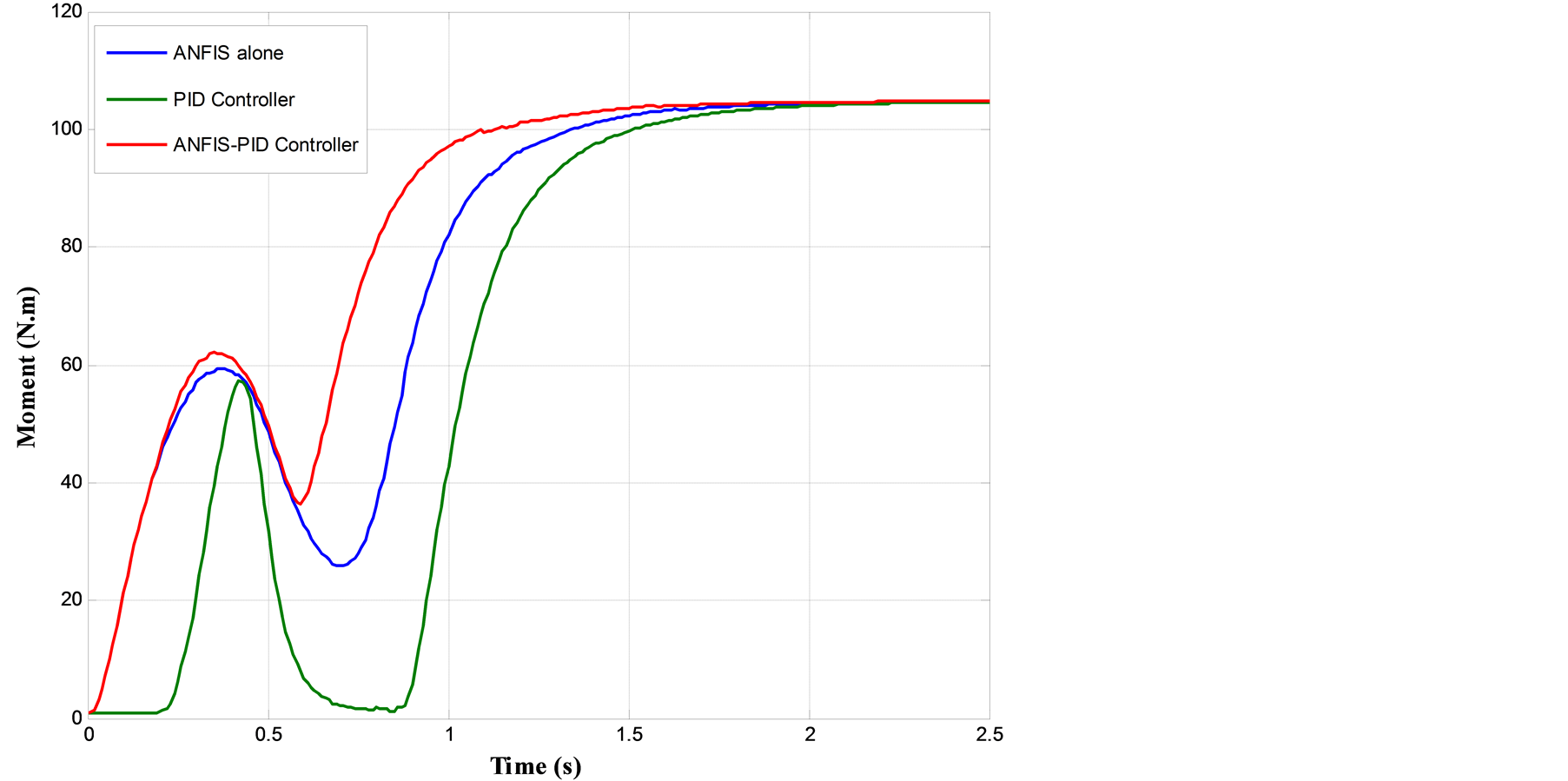
Figure 11. Moments profiles for knee joint based on three types of controllers.
However, since this study is in its preliminary stages, these theoretical results are encouraging and supporting the feasibility of FES for controlling sit to stand movement, a major obstacle to the development of a practical system that achieves this level of performance is that the reference trajectory is limited to sit to stand without upper body support which is not enough to generalize the control system result, in addition more studies are essential for investigating the controller performance during various sit to stand conditions like changing the initial position, using upper body effort, and stimulation more muscles group.
5. Conclusion
Computer simulation results indicate that ANFIS-PID control of sit to stand via using FES of the knee extensors in individuals with paralysis from SCI is feasible and may lead to improved movement stability. The use of computer simulations has provided a platform for iterative design and for this initial evaluation. While the results are encouraging, experimental evaluation on human subjects is required in order to thoroughly evaluate this technique. Since using ANFIS for controlling sit to stand is not studied thoroughly in previous studies, this study highlights the need to use such techniques to improve paraplegic’s daily activities like walking, standing, climbing stairs etc. So this study suggests using such intelligent modeling methods to improve FES control systems.
References
- Aissaoui, R. and Dansereau, J. (1999) Biomechanical Analysis and Modelling of Sit to Stand Task: A Literature Review. IEEE SMC’99 Conference Proceedings, Tokyo, 12-15 October 1999, 141-146.
- Gross, M., Stevenson, P., Charette, S., Pyka, G. and Marcus, R. (1998) Effect of Muscle Strength and Movement Speed on the Biomechanics of Rising from a Chair in Healthy Elderly and Young Women. Gait and Posture, 8, 175- 180. http://dx.doi.org/10.1016/S0966-6362(98)00033-2
- Bromley, I. (2006) Tetraplegia and Parapliegia: A Guide for Physiotherapists. Elsevier, Philadelphia.
- Kantrowitz, A. (1960) Electronic Physiologie Aids: A Report of the Maimonides Hospital. Brooklyn, New York.
- Lynch, C. and Popovic, M. (2008) Functional Electrical Stimulation: Closed-Loop Control of Induced Muscle Contractions. IEEE Control System Magazine, 28, 40-49. http://dx.doi.org/10.1109/MCS.2007.914692
- Kuzelicki, J., Kamnik, R., Bajd, T., Obreza, P. and Benko, H. (2002) Paraplegics Standing up Using Multichannel FES and Arm Support. Journal of Medical Engineering and Technology, 26, 106-110. http://dx.doi.org/10.1080/03091900210123919
- Horch, K. and Dhillon, G. (2004) Neuroprosthetics: Theory and Practice. World Scientific Publishing Co.
- Zhang, K. and Zhu, D. (2004) Simulation Study of FES-Assisted Standing up with Neural Network Control. 26th Annual International Conference of the IEEE EMBS, San Francisco.
- Davoodi, R. and Andrews, B. (1998) Computer Simulation of FES Standing up in Paraplegia: A Self-Adaptive Fuzzy Controller with Reinforcement Learning. IEEE Transactions on Rehabilitation Engineering, 6, 151-161. http://dx.doi.org/10.1109/86.681180
- Abu Bakar, N. and Abdullah, A. (2011) Dynamic Simulation of Sit to Stand Exercise for Paraplegia. IEEE International Conference on Control System, Computing and Engineering, Malaysia, 114-118.
- Wang, S.L. (2001) Motion Simulation with Working Model 2D and MSC. Visual Nastran 4D. Journal of Computer and Information Science and Engineering, 1, 193-196.
- Winter, D. (1990) Biomechanics and Motor Control of Human Movement. 2nd Edition, Wiley-Interscience, New York.
- Rustin, C. (2010) Physiological Modelling and Dynamic Simulation of Human Walking. Faculty Polytechnique de Mons, Mons University, Mons.
- Song, D., Cheng, E., Brown, I., Davoodi, R. and Loeb, G. (2008) Virtual Muscle 4.0.1: Muscle Model for Matlab User’s Manual. Alfred Mann Institute, California.
- Riener, R. and Fuhr, T. (1998) Patient-Driven Control of FES Supported Standing up: A Simulation Study. IEEE Transactions on Rehabilitation Engineering, 6, 113-124. http://dx.doi.org/10.1109/86.681177
- Edrich, T., Riener, R. and Quintern, J. (2000) Analysis of Passive Elastic Joint Moments in Paraplegics. IEEE Transactions on Biomedical Engineering, 47, 1058-1064. http://dx.doi.org/10.1109/10.855933
- Jang, J.-S.R. (1993) ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Transaction on Systems, Man, and Cybernetics, 665-685. http://dx.doi.org/10.1109/21.256541
- Al-Hmouz, A., Shen, J., Al-Hmouz, R. and Yan, J. (2012) Modeling and Simulation of an Adaptive Neuro-Fuzzy Inference System (ANFIS) for Mobile. IEEE Transaction on Learning Technologies, 5, 226-237. http://dx.doi.org/10.1109/TLT.2011.36
- Haugen, F. (2010) Ziegler-Nichols’ Open-Loop Method. TechTeach, 1-7. http://techteach.no/publications/articles/zn_closed_loop_method/zn_closed_loop_method.pdf

