Journal of Biomedical Science and Engineering
Vol.6 No.5A(2013), Article ID:32031,10 pages DOI:10.4236/jbise.2013.65A006
Glucose-stimulated insulin secretion in isolated pancreatic islets: Multiphysics FEM model calculations compared to results of perifusion experiments with human islets*
![]()
1Diabetes Research Institute, University of Miami, Miller School of Medicine, Miami, USA
2Department of Molecular and Cellular Pharmacology, University of Miami, Miller School of Medicine, Miami, USA
Email: #pbuchwald@med.miami.edu
Copyright © 2013 Peter Buchwald, Sirlene R. Cechin. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 5 March 2013; revised 8 April 2013; accepted 11 May 2013
Keywords: COMSOL Multiphysics; Diabetes Mellitus; FEM Model; Glucose-Insulin Dynamics; Hill Equation; Islet Perifusion; Islets of Langerhans
ABSTRACT
Because insulin released by the β-cells of pancreatic islets is the main regulator of glucose levels, the quantitative modeling of their glucose-stimulated insulin secretion is of obvious interest not only to improve our understanding of the processes involved, but also to allow better assessment of β-cell function in diabetic patients or islet transplant recipients as well as the development of improved artificial or bioartificial pancreas devices. We have recently developed a general, local concentrations-based multiphysics computational model of insulin secretion in avascular pancreatic islets that can be used to calculate insulin secretion for arbitrary geometries of cultured, perifused, transplanted, or encapsulated islets in response to various glucose profiles. Here, experimental results obtained from two different dynamic glucose-stimulated insulin release (GSIR) perifusion studies performed by us following standard procedures are compared to those calculated by the model. Such perifusion studies allow the quantitative assessment of insulin release kinetics under fully controllable experimental conditions of varying external concentrations of glucose, oxygen, or other compounds of interest, and can provide an informative assessment of islet quality and function. The time-profile of the insulin secretion calculated by the model was in good agreement with the experimental results obtained with isolated human islets. Detailed spatial distributions of glucose, oxygen, and insulin were calculated and are presented to provide a quantitative visualization of various important aspects of the insulin secretion dynamics in perifused islets.
1. INTRODUCTION
Quantitative models describing the dynamics of glucosestimulated insulin secretion are of obvious interest [1] for both type 1 (insulin-dependent or juvenile-onset) [2] and type 2 (non-insulin dependent or adult-onset) diabetes mellitus. Maintenance of glucose levels within the normal range (typically within 3.5 - 7.0 mM = 60 - 125 mg/ dL in healthy humans) is achieved via the finely-tuned glucose-insulin control system. This mainly relies on bcells located in pancreatic islets that act as a glucose sensor and adjust their insulin output as a function of the blood glucose level. Hence, quantitative models of how healthy b-cells release insulin in response to a change in glucose levels are of critical importance for many different fields such as, for example:
• The development of “artificial pancreas” systems [3] (including automated closed-loop insulin delivery systems [4,5]);
• The development of “bioartificial pancreas” systems [6] (including immune-isolated, encapsulated islets [7-9]);
• The improvement of existing models developed to describe the glucose-insulin regulatory system via organism-level concentrations that are widely used to estimate glucose effectiveness and insulin sensitivity from intravenous glucose tolerance tests (IVGTT) such as curve-fitting models (e.g., the “minimal model” [10] and many others [11-13]) or paradigm models (e.g., HOMA [14,15]);
• The identification of relatively simple indices that 1) are useful indicators of b-cell function in diabetic patients or islet transplant recipients and 2) can be derived from standard readouts such as C-peptide and A1C (e.g., b-score, HOMA-index of b-cell function, secretory unit of islets in transplantation SUIT, Cpeptide/glucose ratio CP/G, or transplant estimated function TEF-see [16] and references therein).
We have recently developed a complex, finite element method (FEM)-based computational insulin secretion model that focuses on the quantitative modeling of local, cellular-level glucose-insulin dynamics and is particularly well suited for the modeling of the insulin secretion of isolated, avascular islets [17]. The model assumes that all nutrient consumption and hormone release rates follow Hill-type sigmoid dependences on local concentrations with insulin secretion rates depending on both the glucose concentration and its time-gradient to account for the secondand first-phase of insulin release, respectively (Figure 1). Hill-type sigmoid dependence has been chosen because this allows a general, easily parameterizable functional dependence that can fit well various biological response curves, including that of insulin secretion in response to glucose (Figure 2). Because hypoxia is also an important limiting factor in avascular islets, oxygen concentrations were also incorporated into the model by extending our previous islet cell oxygen consumption model [18]. Because of the general FEMbased implementation of the model, simulations can be carried out for arbitrary geometries including cultured, perifused, transplanted, and encapsulated islets [17].
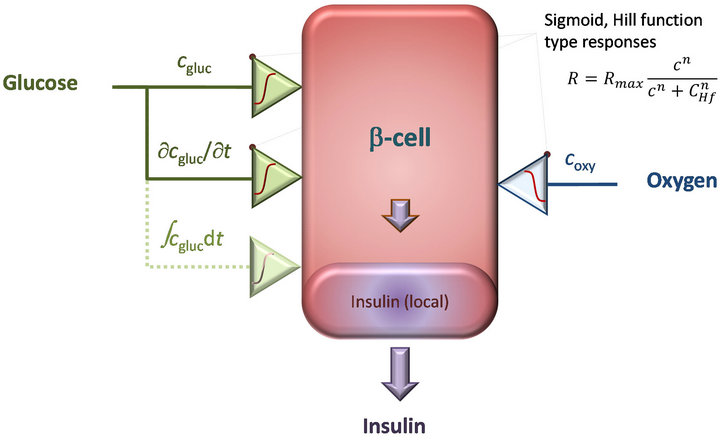
Figure 1. Schematic concept of the present local concentrationbased computational model of glucose-stimulated insulin release in b-cells [17]. The model is implemented within a general framework of sigmoid proportional-integral-derivative (SPID) controller [17] with insulin secretion determined by glucose concentrations, but also influenced by the local availability of oxygen.

Figure 2. Glucose-dependence of insulin secretion rate in perifused islets. The Hill-type sigmoid dependence used in the present local concentration-dependent FEM-based model (Equations (2) and (4); n = 2.5, CHf, gluc = 7 mM; blue line) [17] is shown here in comparison with the experimental data obtained for perifused human islets (blue diamonds, u) [24] and isolated rat pancreas (blue circles, ○) [25].
While there has been considerable work on modeling insulin secretion (especially for encapsulated islets, e.g., [19-23]), the present model has the unique advantage that allows the coupling of both convective and diffusive transport with reactive rates for arbitrary geometries with no symmetry restrictions. Furthermore, the present model also incorporates a comprehensive approach to account not only for firstand second-phase insulin responses, but also for both the glucoseand the oxygendependence of insulin release.
Here, we compare insulin secretion values calculated by the present model with experimental results obtained from two different dynamic glucose-stimulated insulin release (GSIR) perifusion studies performed in our Institute following standard procedures [26,27]. Such perifusion studies (Figure 3) allow the quantitative assessment of insulin release kinetics under fully controllable experimental conditions of varying external concentrations of glucose, oxygen, or other compounds of interest, and are now routinely used to assess islet quality and function [28-30].
2. MATERIALS AND METHODS
2.1. Islet Perifusion
Islets were isolated at the Diabetes Research Institute’s Cell Processing Facility or other centers participating in the National Institute of Health Islet Cell Resources (ICR) as described before [26,31,32]. Briefly, human pancreata were obtained from multi-organ cadaveric donors and processed with the automated Ricordi method [33]. The

Figure 3. The general concept of glucose-stimulated insulin secretion (GSIR) perifusion assays used to assess islet quality and function. The present simplified design with only one or two representative spherical islets has been used as the basic geometry of the present model [17] (cf. Figure 6).
pancreas is “cannulated” through the duct to allow for the enzyme to distend the organ. Then, it is placed into the Ricordi chamber and continuously digested in order to obtain fragments of progressively decreasing sizes [31]. The enzyme is activated by a heating circuit, and a continuous flow allows the islets to be collected [33]. Islets are purified using a computerized semi-automated cell processor (COBE) at a temperature of 4˚C and a Ficol-based density gradient [32]. The highly purified islets are generally contained in the top layer, while the less pure islets settle on the bottom layers of the gradient. Following isolation, islets are cultured at 37˚C in humidified mixed 95% air 5% CO2 in non-tissue treated flasks with Miami-defined media 1 (MM1; Mediatech) containing human serum albumin [27,34]. After 24 h of culture, islets are collected and divided in different culture conditions (1500 - 2000 IEQ per condition) for incubation with test compounds (here, loteprednol etabonate [26] or exenatide [27]) present at different concentrations.
The dynamic glucose-stimulated insulin release (GSIR) perifusion experiments were performed using a custom built apparatus (BioRep Technologies, Inc., Miami, FL). Islets aliquots were loaded in Perspex microcolums, between two layers of acrylamide-based microbead slurry (Bio-Gel P-4, Bio-Rad Laboratories, Hercules, CA). Perifusing buffer containing 125 mM NaCl, 5.9 mM KCl, 1.28 mM CaCl2, 1.2 mM MgCl2, 25 mM HEPES, 0.1% bovine serum albumin, and 3 mM glucose at 37˚C with selected glucose (low = 3 mM; high = 11 mM) or KCl (25 mM) concentrations was circulated through the columns at a rate of 100 mL/min. After 45 - 60 minutes of washing with the low glucose solution for stabilization, the islets were stimulated with the following sequence: 5 min of low glucose, 10 min of high glucose, 15 min of low glucose, 5 min of KCl, and 5 min of low glucose. Serial samples (100 mL) were collected every minute from the outflow tubing of the columns in an automatic fraction collector designed for a multi-well plate format. The sample container harboring the islets and the perifusion solutions were kept at 37˚C in a built-in temperature controlled chamber. The perifusate in the collecting plate was kept at <4˚C to preserve the integrity of the analytes in the perifusate. Insulin concentrations were determined with a commercially available ELISA kit (Mercodia Inc., Wiston Salem, NC); values used here are averages across the different conditions used in the two different experimental settings.
2.2. Computational Model
For computational modeling, our previously developed local concentration-based insulin secretion model has been used here; a detailed description of its implementation and parameterization has been published [17]. Here, only a brief summary, needed to interpret and understand the results, is included. A total of four concentrations are used for (convective and diffusive) mass transport modeling with their corresponding equations (application modes): glucose, oxygen, and “local” and released insulin (cgluc, coxy, cinsL, cins). Diffusion is assumed to be governed by the generic diffusion equation in its nonconservative formulation (incompressible fluid) [35]:
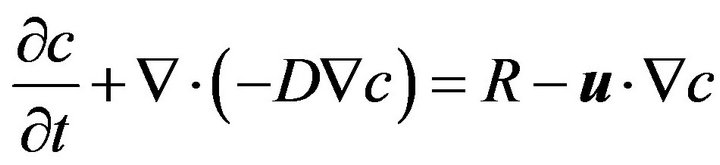 (1)
(1)
where, c denotes the concentration [mol×m−3] and D the diffusion coefficient [m2×s−1] of the species of interest, R the reaction rate [mol×m−3×s−1], u the velocity field [m×s−1], and Ñ the standard del (nabla) operator  . The following diffusion coefficients are used: oxygen, Doxy, w = 3.0 ´ 10−9 m2×s−1 in aqueous media and Doxy, t = 2.0 ´ 10−9 m2×s−1 in islet tissue; glucose, Dgluc, w = 9.0 ´ 10−10 m2×s−1 and Dgluc, t = 3.0 ´ 10−10 m2×s−1; insulin, Dins, w = 1.5 ´ 10−10 m2×s−1 and Dins, t = 5 ´ 10−11 m2×s−1.
. The following diffusion coefficients are used: oxygen, Doxy, w = 3.0 ´ 10−9 m2×s−1 in aqueous media and Doxy, t = 2.0 ´ 10−9 m2×s−1 in islet tissue; glucose, Dgluc, w = 9.0 ´ 10−10 m2×s−1 and Dgluc, t = 3.0 ´ 10−10 m2×s−1; insulin, Dins, w = 1.5 ´ 10−10 m2×s−1 and Dins, t = 5 ´ 10−11 m2×s−1.
As an important part of the model, all consumption and release rates are assumed to follow Hill-type dependence (generalized Michaelis-Menten kinetics) on the local concentrations because this provides a convenient and easily parameterizable mathematical function for biological/pharmacological applications:
 (2)
(2)
Parameters here are Rmax, the maximum reaction rate [mol×m–3×s–1], CHf, the concentration corresponding to half-maximal response [mol×m–3], and n, the Hill slope characterizing the shape of the response. The parameter values used for the different release and consumption functions (i.e., insulin, glucose, oxygen; e.g., CHf, glucCHf, oxy, etc.) are different; their values used in the model are summarized in Table 1 of [17].
For avascular islets, oxygen availability is a main limiting factor because the solubility of oxygen in culture media or in tissue is much lower than that of glucose; hence, available oxygen concentrations are usually much more limited (e.g., around 0.05 - 0.2 mM for oxygen vs 3 - 15 mM for glucose assuming physiologically relevant conditions). In this context, it is important to note that, to account for the increased metabolic demand of insulin release and production at higher glucose concentrations, the model also includes a dependence of the oxygen consumption (Roxy) on the local glucose concentration via a modulating function jo, g (cgluc):
 (3)
(3)
Undeniably, the most important part of the model is the functional form describing the glucose-dependence of the insulin secretion rate, Rins. For this purpose, a Hill equation providing a sufficiently abrupt sigmoid response proved adequate; the shape of its dependence on cgluc is shown in Figure 2. The corresponding function used here to describe the glucose-insulin dynamics of the second-phase response is a version of Equation (2):
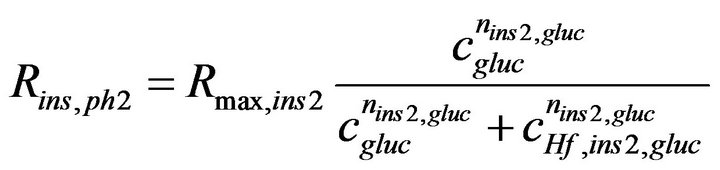 (4)
(4)
with nins2, gluc = 2.5, CHf, ins2, gluc = 7 mM, and Rmax, ins2 = 3.0 ´ 10−5 mol×m−3×s−1. For the first-phase response, a Hill-type sigmoid component that depends on the glucose time-gradient (ct = ¶cgluc/¶t) is incorporated into the model. This is non-zero only when the glucose concentration is increasing, i.e., only when ct > 0. For a correct time-scale of insulin release, an additional “local” insulin compartment had to be added (Figure 1); insulin is assumed to be first secreted into this compartment and then released from here following a first order kinetics 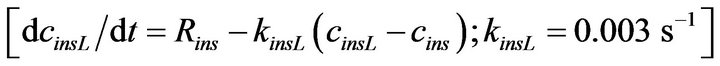 ; for details, see [17].
; for details, see [17].
Finally, to also incorporate media flow, these convection and diffusion models are coupled to a fluid dynamics model. For this purpose, the incompressible NavierStokes model for Newtonian flow (constant viscosity) is used to calculate the velocity field u resulting from convection [35]:
 (5)
(5)
The first equation is the momentum balance, and the second one is the equation of continuity for incompressible fluids. Standard notation is used with r denoting density [kg×m−3], h viscosity [kg×m−1×s−1 = Pa×s], p pressure [Pa, N×m−2, kg×m−1×s−2], and F volume force [N×m−3, kg×m−2×s−2]. The flowing media is assumed to be an essentially aqueous media at body temperature (37˚C). Incoming media is assumed to be in equilibrium with atmospheric oxygen and, thus, to have an oxygen concentration of coxy, in = 0.200 mol×m−3 (mM) corresponding to 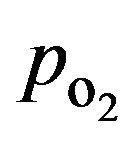 ≈ 140 mmHg.
≈ 140 mmHg.
All models were implemented in COMSOL Multiphysics 4.2 (COMSOL Inc., Burlington, MA) and solved as time-dependent (transient) problems allowing intermediate time-steps for the solver as described before. Two spherical islets of 100 and 150 mm diameter are used for modeling and they are placed in a 2D crosssection of a cylindrical tube with fluid flowing from left to right. Our recent analysis of the size distribution of (isolated) human islets based on data from more than 200 isolations [36] found that it is well-described by a Weibull distribution function and that while most islets are small, most islet mass is contributed by larger islets (Figure 4). The expected value of islet diameter was found to be 95 mm, whereas the expected value of islet volume was found to be 1.2 ´ 106 mm3, which corresponds to the volume of an islet with d = 133 mm; hence, the two sizes used for modeling here (d = 100 and 150 mm) can be considered as representative for human islets used in perifusion assays.
3. RESULTS AND DISCUSSION
The experimental insulin secretion data of isolated human islets used here were obtained from dynamic glucose-stimulated insulin release (GSIR) perifusion experiments performed using a custom built apparatus as described in the Materials and Method section. Such perifusion experiments are regularly used in our Institute for the quantitative assessment of islet quality and function [30] including these studies that were investigating the effects of loteprednol etabonate and exenatide, respectively on islet function [26,27]. Here, the experimental results obtained from these dynamic GSIR perifusion studies are compared with the insulin secretion values calculated by the present model [17]. Total insulin outflows following a 10-min high glucose (11 mM) stimulation from both experiments are shown in Figure 5 together with the model calculated prediction for a corresponding glucose step and assuming atmospheric oxygen (coxy = 0.2 mM; 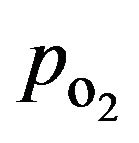 ≈ 140 mmHg).
≈ 140 mmHg).
As can be seen in Figure 5, there is good agreement between the model-calculated shape of the time-response of insulin secretion and that of the two different sets of experimental determinations in human islets. Because the

Figure 4. The size distribution of human pancreatic islets as found in our recent study of data from more than 200 isolations. The probability density of the number (N, blue) and volume or mass (V, red) of human islets is shown as a function of diameter (d) assuming a Weibull distribution function.
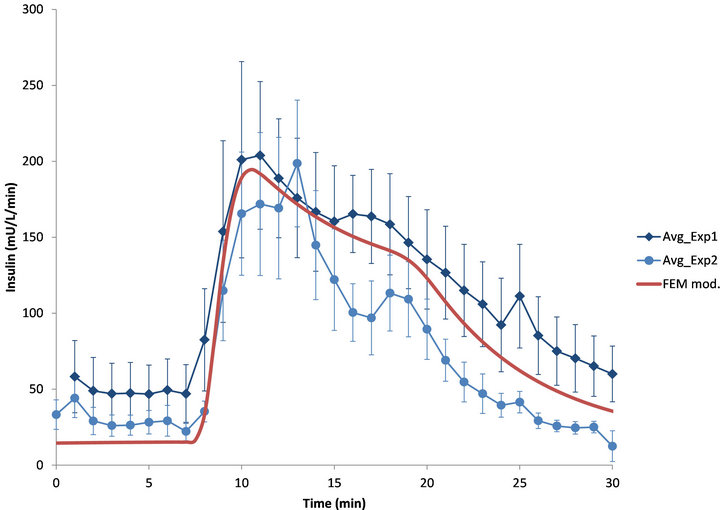

Figure 5. Experimental and model-calculated glucose-stimulated insulin release in perifused human islets in response to a 10-min glucose step (3 mM to 11 mM) in the perifusing solution. Values calculated with the present model (red line, –) are shown together with experimental data (average ± SD) from two different sets of experiments with human islets (blue diamonds u [27] and blue disks l [26]).
high-glucose stimulation used in these standard islet assessment protocols is of only a 10-min duration, the firstand second-phases of insulin secretion are not well separated, but the overall shapes of the insulin responses are in good agreement (calculated amplitude, which is a function of the actual islet mass present, was adjusted for best fit). The model seems to account well for both the rapid increase in insulin secretion following the glucose step-up (3 mM ® 11 mM) and the rate of its decline following the glucose step-down.
An important advantage of the present computational model is that it not only makes possible detailed simulations for arbitrary inflow conditions and islet arrangements, but also the easy generation of various corresponding 2D or 3D visualizations. For example, Figure 6 shows calculated insulin secretion rates at a time-point corresponding to an increase in glucose concentration as seen by the islets. It clearly shows a delay in response in the middle and back-sides of the larger islet that have not yet been reached by the higher glucose levels.
Figure 7 shows the calculated spatial distributions of insulin and oxygen concentrations within the islets and the perifusion chamber during the decrease of the incoming glucose concentration. For the present conditions (atmospheric oxygen; i.e.,  = 140 mmHg in the incoming media), the core regions of not too large islets (such as those shown here; d = 100 and 150 mm) are still sufficiently oxygenized; hence, their insulin secretions are not yet limited. However, we have shown before [17] that this is no longer true for hypoxic conditions or for larger islets. In such cases, the insulin secretion of the core regions could be severely limited and larger islets could perform less efficiently than smaller islets since the more severe oxygen limitation in their core region restricts insulin secretion to only the outside shell.
= 140 mmHg in the incoming media), the core regions of not too large islets (such as those shown here; d = 100 and 150 mm) are still sufficiently oxygenized; hence, their insulin secretions are not yet limited. However, we have shown before [17] that this is no longer true for hypoxic conditions or for larger islets. In such cases, the insulin secretion of the core regions could be severely limited and larger islets could perform less efficiently than smaller islets since the more severe oxygen limitation in their core region restricts insulin secretion to only the outside shell.
In conclusion, our local concentration-based multiphysics insulin secretion computational model can account well for the insulin secretion profile of isolated,

Figure 6. Calculated insulin secretion rate within the islets and the perifusion chamber for two illustrative perifused islets with diameters of 100 and 150 mm (flow from left to right) under normoxic conditions. Data shown as surface plot are total insulin secretion rates (color-coded from green for low to red for high. Streamlines show the flow of the perifusion fluid (color-coded for velocity) and colored contour lines show isolevels for the perifusing glucose (from light blue for low to light red for high). Model calculated insulin secretion is shown during the increase of the glucose concentration from 3 mM to 11 mM; the middle and back side of the larger islet has not yet been reached by the higher glucose hence insulin secretion there is less intense.

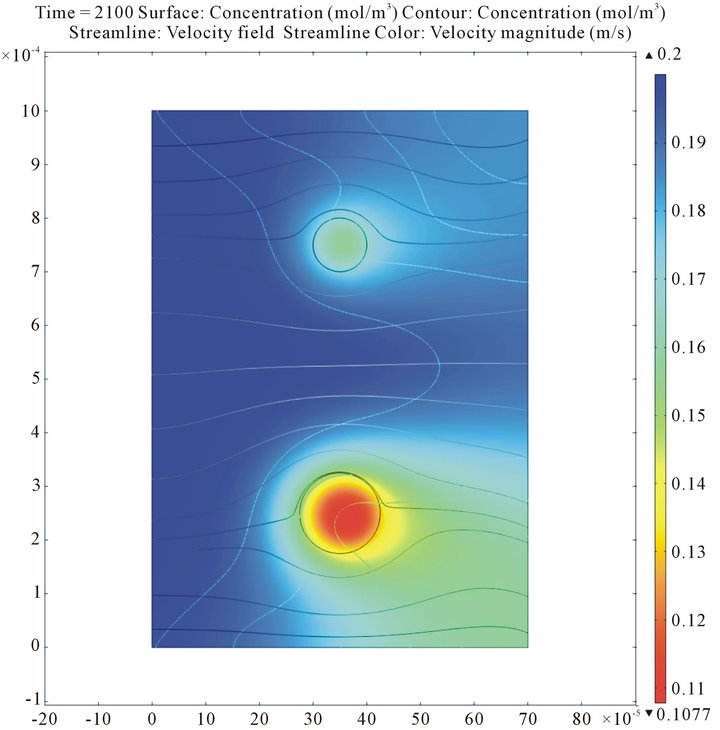

Figure 7. Calculated insulin and oxygen concentrations within the islets and the perifusion chamber during the decrease of the incoming glucose concentration. Data shown as surface plots are insulin concentrations (color-coded from blue for low to red for high; top figure, previous page), and oxygen concentrations (color-coded from red for low to blue for high; bottom figure, previous page). The figure above combines the same information into a 3D representation with the oxygen concentration as the color code and the insulin concentration incorporated as height data.
avascular human islets obtained in standard GSIR perifusion assays. Detailed spatial distributions of all concentrations of interest can be obtained and visualized making it possible to investigate the quantitative aspects of the insulin secretion dynamics in a much more convenient manner and allowing user-friendly computational modeling for arbitrary conformations of cultured, perifused, transplanted, or encapsulated islets.
4. ACKNOWLEDGEMENTS
The financial support of the Diabetes Research Institute Foundation (www.diabetesresearch.org) that made this work possible is gratefully acknowledged.
REFERENCES
- Hallgreen, C.E., Korsgaard, T.V., Hansen, R.N., and Colding-Jørgensen, M. (2008) The glucose-insulin control system. In: Bertau, M., Mosekilde, E. and Westerhoff, H.V., Eds., Biosimulation in Drug Development, WileyVCH, Weinheim, 141-196.
- van Belle, T.L., Coppieters, K.T. and von Herrath, M.G. (2011) Type 1 diabetes: Etiology, immunology, and therapeutic strategies. Physiological Reviews, 91, 79-118. doi:10.1152/physrev.00003.2010
- Galletti, P.M., Colton, C.K., Jaffrin, M. and Reach, G. (2006) Artificial pancreas. In: Bronzino, J.D., Ed., The Biomedical Engineering Handbook. Tissue Engineering and Artificial Organs, 3rd Edition, CRC Press, Boca Raton, 71.71-71.18.
- Steil, G.M., Panteleon, A.E. and Rebrin, K. (2004) Closed-loop insulin delivery-the path to physiological glucose control. Advanced Drug Delivery Reviews, 56, 125-144. doi:10.1016/j.addr.2003.08.011
- Hovorka, R. (2006) Continuous glucose monitoring and closed-loop systems. Diabetic Medicine, 23, 1-12. doi:10.1111/j.1464-5491.2005.01672.x
- Fort, A., Fort, N., Ricordi, C. and Stabler, C.L. (2008) Biohybrid devices and encapsulation technologies for engineering a bioartificial pancreas. Cell Transplantation, 17, 997-1003. doi:10.3727/096368908786991498
- Silva, A.I., de Matos, A.N., Brons, I.G. and Mateus, M. (2006) An overview on the development of a bio-artificial pancreas as a treatment of insulin-dependent diabetes mellitus. Medicinal Research Reviews, 26, 181-222. doi:10.1002/med.20047
- Teramura, Y. and Iwata, H. (2010) Bioartificial pancreas microencapsulation and conformal coating of islet of Langerhans. Advanced Drug Delivery Reviews, 62, 827- 840. doi:10.1016/j.addr.2010.01.005
- O'Sullivan, E.S., Vegas, A., Anderson, D.G. and Weir, G.C. (2011) Islets transplanted in immunoisolation devices: A review of the progress and the challenges that remain. Endocrine Reviews, 32, 827-844. doi:10.1210/er.2010-0026
- Bergman, R.N., Ider, Y.Z., Bowden, C.R. and Cobelli, C. (1979) Quantitative estimation of insulin sensitivity. American Journal of Physiology—Endocrinology and Metabolism, 236, E667-E677.
- Toffolo, G.M. and Cobelli, C. (2001) Insulin modeling. In: Carson, E. and Cobelli, C., Eds., Modeling Methodology for Physiology and Medicine, Academic Press, San Diego, 305-335. doi:10.1016/B978-012160245-1/50012-X
- Makroglou, A., Li, J. and Kuang, Y. (2006) Mathematical models and software tools for the glucose-insulin regulatory system and diabetes: An overview. Applied Numerical Mathematics, 56, 559-573. doi:10.1016/j.apnum.2005.04.023
- Boutayeb, A. and Chetouani, A. (2006) A critical review of mathematical models and data used in diabetology. BioMedical Engineering OnLine, 5, 43. doi:10.1186/1475-925X-5-43
- Matthews, D.R., Hosker, J.P., Rudenski, A.S., Naylor, B.A., Treacher, D.F. and Turner, R.C. (1985) Homeostasis model assessment: Insulin resistance and beta-cell function from fasting plasma glucose and insulin concentrations in man. Diabetologia, 28, 412-419. doi:10.1007/BF00280883
- Wallace, T.M., Levy, J.C. and Matthews, D.R. (2004) Use and abuse of HOMA modeling. Diabetes Care, 27, 1487-1495. doi:10.2337/diacare.27.6.1487
- Caumo, A., Maffi, P., Nano, R., Luzi, L., Hilbrands, R., Gillard, P., Jacobs-Tulleneers-Thevissen, D., Secchi, A., Keymeulen, B., Pipeleers, D. and Piemonti, L. (2011) Comparative evaluation of simple indices of graft function after islet transplantation. Transplantation, 92, 815- 821. doi:10.1097/TP.0b013e31822ca79b
- Buchwald, P. (2011) A local glucose-and oxygen concentration-based insulin secretion model for pancreatic islets. Theoretical Biology and Medical Modelling, 8, 20. doi:10.1186/1742-4682-8-20
- Buchwald, P. (2009) FEM-based oxygen consumption and cell viability models for avascular pancreatic islets. Theoretical Biology and Medical Modelling, 6, 5. doi:10.1186/1742-4682-6-5
- Reach, G. and Jaffrin, M.Y. (1990) Kinetic modelling as a tool for the design of a vascular bioartificial pancreas: Feedback between modelling and experimental validation. Comput. Computer Methods and Programs in Biomedicine, 32, 277-285. doi:10.1016/0169-2607(90)90110-U
- Pillarella, M.R. and Zydney, A.L. (1990) Theoretical analysis of the effect of convective flow on solute transport and insulin release in a hollow fiber bioartificial pancreas. Journal of Biomechanical Engineering, 112, 220-228. doi:10.1115/1.2891175
- Tziampazis, E. and Sambanis, A. (1995) Tissue engineering of a bioartificial pancreas: Modeling the cell environment and device function. Biotechnology Progress, 11, 115-126. doi:10.1021/bp00032a001
- Buladi, B.M., Chang, C.C., Belovich, J.M. and Gatica, J.E. (1996) Transport phenomena and kinetics in an extravascular bioartificial pancreas. AIChE Journal, 42, 2668-2682. doi:10.1002/aic.690420928
- Dulong, J.L., and Legallais, C. (2005) What are the relevant parameters for the geometrical optimization of an implantable bioartificial pancreas? Journal of Biomechanical Engineering, 127, 1054-1061. doi:10.1115/1.2073407
- Henquin, J.C., Dufrane, D. and Nenquin, M. (2006) Nutrient control of insulin secretion in isolated normal human islets. Diabetes, 55, 3470-3477. doi:10.2337/db06-0868
- Grodsky, G.M. (1972) A threshold distribution hypothesis for packet storage of insulin and its mathematical modeling. Journal of Clinical Investigation, 51, 2047- 2059. doi:10.1172/JCI107011
- Bocca, N., Pileggi, A., Molano, R.D., Marzorati, S., Wu, W., Bodor, N., Ricordi, C. and Buchwald, P. (2008) Soft corticosteroids for local immunosuppression: Exploring the possibility for the use of loteprednol etabonate in islet transplantation. Pharmazie, 63, 226-232.
- Cechin, S.R., Perez-Alvarez, I., Fenjves, E., Molano, R.D., Pileggi, A., Berggren, P.O., Ricordi, C. and Pastori, R.L. (2012) Anti-inflammatory properties of exenatide in human pancreatic islets. Cell Transplantation, 21, 633- 648. doi:10.3727/096368911X576027
- Dionne, K.E., Colton, C.K. and Yarmush, M.L. (1993) Effect of hypoxia on insulin secretion by isolated rat and canine islets of Langerhans. Diabetes, 42, 12-21. doi:10.2337/diabetes.42.1.12
- Sweet, I.R., Khalil, G., Wallen, A.R., Steedman, M., Schenkman, K.A., Reems, J.A., Kahn, S.E. and Callis, J.B. (2002) Continuous measurement of oxygen consumption by pancreatic islets. Diabetes Technology & Therapeutics, 4, 661-672. doi:10.1089/152091502320798303
- Cabrera, O., Jacques-Silva, M.C., Berman, D.M., Fachado, A., Echeverri, F., Poo, R.E., Khan, A., Kenyon, N.S., Ricordi, C., Berggren, P.-O. and Caicedo, A. (2008) Automated, high-throughput assays for evaluation of human pancreatic islet function. Cell Transplantation, 16, 1039- 1048. doi:10.3727/000000007783472408
- Pileggi, A., Ricordi, C., Kenyon, N.S., Froud, T., Baidal, D.A., Kahn, A., Selvaggi, G. and Alejandro, R. (2004) Twenty years of clinical islet transplantation at the Diabetes Research Institute—University of Miami. Clinical Transplantation, 2004, 177-204.
- Ichii, H., Pileggi, A., Molano, R.D., Baidal, D.A., Khan, A., Kuroda, Y., Inverardi, L., Goss, J.A., Alejandro, R. and Ricordi, C. (2005) Rescue purification maximizes the use of human islet preparations for transplantation. American Journal of Transplantation, 5, 21-30. doi:10.1111/j.1600-6143.2005.00698.x
- Ricordi, C., Lacy, P.E., Finke, E.H., Olack, B.J. and Scharp, D.W. (1988) Automated method for isolation of human pancreatic islets. Diabetes, 37, 413-420. doi:10.2337/diabetes.37.4.413
- Ichii, H., Sakuma, Y., Pileggi, A., Fraker, C., Alvarez, A., Montelongo, J., Szust, J., Khan, A., Inverardi, L., Naziruddin, B., Levy, M.F., Klintmalm, G.B., Goss, J.A., Alejandro, R. and Ricordi, C. (2007) Shipment of human islets for transplantation. American Journal of Transplantation, 7, 1010-1020. doi:10.1111/j.1600-6143.2006.01687.x
- Comsol, AB (2007) COMSOL multiphysics modeling guide, version 3.4. COMSOL AB.
- Buchwald, P., Wang, X., Khan, A., Bernal, A., Fraker, C., Inverardi, L. and Ricordi, C. (2009) Quantitative assessment of islet cell products: Estimating the accuracy of the existing protocol and accounting for islet size distribution. Cell Transplantation, 18, 1223-1235. doi:10.3727/096368909X476968.
NOTES
*Competing interests: There are nofinancial competing interests for this article.
Authors’ contributions: PB conceived the study and designed, calibrated, and implemented the computational model. SRC performed perifusion experiments and analyzed the corresponding data. All authors contributed to the writing and review of the manuscript.
#Corresponding author.

