Intelligent Information Management
Vol.2 No.7(2010), Article ID:2218,6 pages DOI:10.4236/iim.2010.27053
New Investigative Findings from the Debiased Converted-Measurement Kalman Filter
1Cobham Analytic Solutions, 401 Diamond Drive, Huntsville, USA
2Department of Electrical and Computer Engineering, University of Alabama in Huntsville, Huntsville, USA
E-mail: john.spitzmiller@cobham.com, adhami@ece.uah.edu
Received March 5, 2010; revised April 19, 2010; accepted May 27, 2010
Keywords: tracking, converted measurements, Kalman filter, debiased CMKF, polar-to-Cartesian conversion
Abstract
The original algorithm for the 2-D debiased converted-measurement Kalman filter (CMKF) specified, with incorrect mathematical justification, a requirement for evaluating the average true bias and covariance with the best available polar estimate, rather than exclusively with the polar measurement. Even though this original algorithm yields better tracking performance than the debiased-CMKF algorithm which evaluates the average true bias and covariance exclusively with the polar measurement, this paper shows the specified requirement compromises the statistical consistency between the debiased converted measurement’s error and the average true covariance. To resolve this apparent contradiction, this paper provides the correct empirical explanation for the tracking-performance improvement obtained by the specified requirement.
1. Introduction
In the original paper describing the 2-D debiased converted-measurement Kalman filter (CMKF) [1], Lerro and Bar-Shalom derived approximate but practical expressions for the converted measurement’s error bias and covariance that depend on only the polar target-position measurement and the polar measurement’s error statistics. They termed these quantities the “average true bias” and the “average true covariance,” respectively. In order to improve the practical debiased CMKF’s dynamic tracking performance, Lerro and Bar-Shalom further specified the additional requirement of evaluating the average true bias [2] and the average true covariance [1,2] using the best available polar estimate rather than evaluating them exclusively with the polar measurement. To provide a practical means of meeting this additional requirement, Lerro and Bar-Shalom presented a simple test which chooses the more accurate of the polar measurement and predicted polar estimate (obtained via nonlinear transformation of the CMKF’s predicted Cartesian position components) based on the sizes of the respective error covariances in Cartesian coordinates. (Note that, strictly speaking, [1] only calls for the average true covariance to be evaluated with the best available polar estimate. However, [2] confirms that both the average true bias and the average true covariance should be evaluated with the best available polar estimate; the omitted call for evaluating the average true bias with the best available polar estimate was a publishing oversight. Furthermore, the simulation results of [1] were obtained by evaluating both the average true bias and the average true covariance with the best available polar estimate [2].)
Lerro and Bar-Shalom demonstrated good statistical consistency between the debiased converted measurement’s error and the average true covariance for the “static case” when both the average true bias and covariance were evaluated exclusively with the polar measurement. They also demonstrated that, when compared with the previously dominant 2-D extended Kalman filter, the fully specified 2D debiased CMKF’s algorithm yields improved tracking performance and statistical consistency between the actual state-estimate error and the state-estimate-error covariance. However, they did not quantify the additional specification’s impact on the statistical consistency between the debiased converted measurement’s error and the average true covariance for the “dynamic case” when both the average true bias and covariance are usually [1] evaluated with the polar prediction—having error statistics significantly different from those of the polar measurement [3]— during tracking.
The stated reason in [1] for the additional requirement of using the best available polar estimate was that the average true covariance had been shown to be “a function of the [true] target range and bearing as well as the error in their respective measurements.” The average true covariance is in fact a function of the polar measurement whose components are respectively given by (1) of [1] as the sum of the true polar quantities and the polarmeasurement errors. However, the average true bias and covariance expressions were derived to properly account only for the fact that the polar measurement’s error components are zero-mean, Gaussian, and uncorrelated; the expressions do not properly account for the polar prediction’s error whose statistics are non-Gaussian and correlated [3]. From another point of view, whereas using the best available polar estimate in a function of the true polar position would be a mathematically justified approximation technique, substituting a more accurate polar estimate for the polar measurement of which the average true bias and covariance are functions is not mathematically justified. From either point of view, the only mathematically justified polar estimate to use in the evaluation of the average true bias and covariance is the polar measurement itself. Thus, the stated reason for the debiased CMKF’s additional requirement cannot be correct.
This paper provides the correct empirical explanation (rather than a mathematical justification) for the improved tracking performance in the simulated tracking scenarios of [1] obtained by evaluating the average true bias and covariance with a polar estimate less uncertain than the polar measurement. Specifically, we show that evaluating the average true bias and covariance with a polar estimate less uncertain than the polar measurement results in bias and covariance expressions which more closely approximate the ideal bias and covariance than does exclusively evaluating the average true bias and covariance with the polar measurement.
Section 2 provides a concise review of the 2-D debiased CMKF’s algorithm. In Section 3 we show three important, empirical performance characteristics resulting from evaluating the average true bias and covariance with polar estimates of varying quality. First, we confirm that, as claimed by [1], the tracking performance improves with the quality of the polar estimate used to evaluate the average true bias and covariance. Second, we demonstrate that statistical inconsistency between the debiased converted measurement’s error and the average true covariance results when the average true bias and covariance are evaluated with polar estimates having error statistics different from those of the polar measurement’s error. Third, we resolve the apparent contradiction between the tracking improvement and the statistical inconsistency which result when the average true bias and covariance are evaluated with polar estimates more accurate than the polar measurement by showing the average true bias and covariance actually become respectively closer, on average, to the true bias and covariance. This third characteristic underlies the superior tracking performance of the debiased CMKF of [1,2] over the debiased CMKF which evaluates the average true bias and covariance exclusively with polar measurement.
2. Technical Background
A sensor remotely measures a target’s position and produces the polar position measurement
 . (1)
. (1)
In (1), 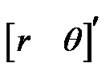 is the target’s true position in polar coordinates (range and bearing), and
is the target’s true position in polar coordinates (range and bearing), and 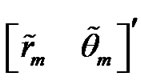 is [1] a white, zero-mean, Gaussian measurement noise with covariance
is [1] a white, zero-mean, Gaussian measurement noise with covariance
 . (2)
. (2)
Since the target’s true Cartesian position is
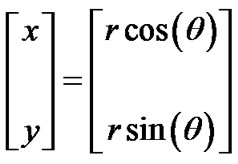 , (3)
, (3)
the error 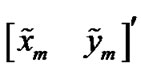 of the raw converted measurement
of the raw converted measurement
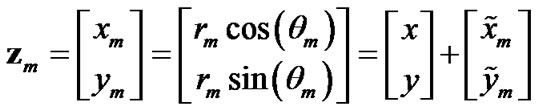 (4)
(4)
is
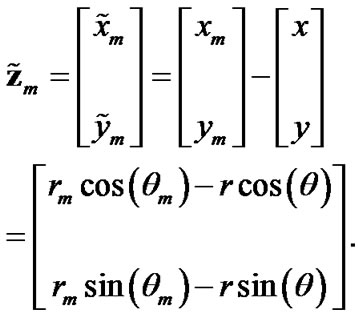 (5)
(5)
Lerro and Bar-Shalom [1] derived a closed-form expression for the raw converted measurement’s true error bias
 , (6)
, (6)
with which (4) can be debiased to produce an unbiased converted measurement. They also derived a closed-form expression for the corresponding debiased converted measurement’s true error covariance
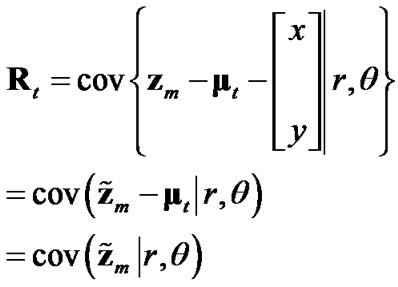 (7)
(7)
which is necessary for the standard Kalman-filter algorithm. However, since the closed-form expressions for (6) and (7) require the target’s true range and bearing [1], realizable CMKFs cannot use these expressions.
In response to the impracticality of using (6) and (7), Lerro and Bar-Shalom [1] proposed what is now known as the 2D debiased CMKF. The 2D debiased CMKF approximates the raw converted measurement’s true error bias with the “average true bias” of the convertedmeasurement error [1]
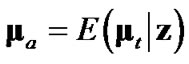 (8)
(8)
which requires the polar measurement rather than the target’s true position. Thus, the debiased converted measurement that is actually input to the 2D debiased CMKF’s tracking algorithm is
 . (9)
. (9)
Similarly, the 2D debiased CMKF approximates the debiased converted measurement’s true error covariance with the “average true covariance” of the convertedmeasurement error [1]
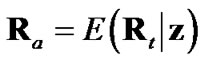 (10)
(10)
which, like the average true bias, requires the polar measurement rather than the target’s true position. Note that the procedure of first conditioning the bias and covariance on the target’s true position and then conditioning the resulting expressions’ means on the polar measurement is known as “nested conditioning” [4].
As a final specification for the 2D debiased CMKF, Lerro and Bar-Shalom called for using the best available polar estimate, 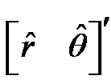 , for the evaluation of
, for the evaluation of 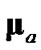 [2] and
[2] and 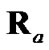 [1,2] during tracking. Lerro and Bar-Shalom identified the polar measurement itself and the polar position prediction (obtained via nonlinear transformation of the CMKF’s Cartesian position prediction) as the only such practically available polar estimates. Lerro and BarShalom specified a simple test that, at each processing index, chooses the polar estimate having the error covariance with the smaller “size” in Cartesian coordinates as measured by the matrix determinant. Mathematically, the employed polar estimate,
[1,2] during tracking. Lerro and Bar-Shalom identified the polar measurement itself and the polar position prediction (obtained via nonlinear transformation of the CMKF’s Cartesian position prediction) as the only such practically available polar estimates. Lerro and BarShalom specified a simple test that, at each processing index, chooses the polar estimate having the error covariance with the smaller “size” in Cartesian coordinates as measured by the matrix determinant. Mathematically, the employed polar estimate, 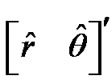 , is selected according to
, is selected according to
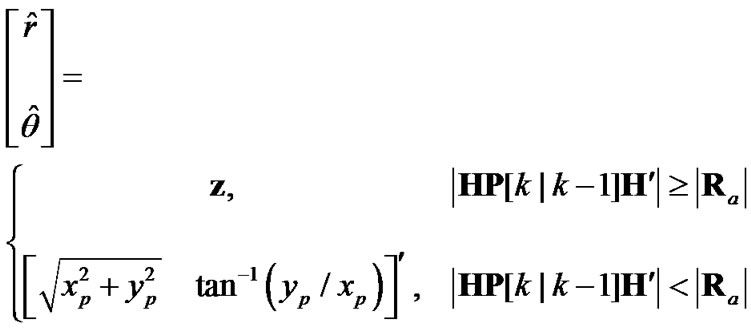
(11)
where 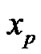 and
and 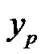 are the position components of the CMKF’s prediction in the x and y directions, respectively, H is the matrix which extracts the CMKF’s Cartesian position prediction from its Cartesian state prediction, and
are the position components of the CMKF’s prediction in the x and y directions, respectively, H is the matrix which extracts the CMKF’s Cartesian position prediction from its Cartesian state prediction, and 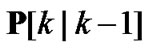 is the predicted state-estimate-error covariance. In (11),
is the predicted state-estimate-error covariance. In (11), 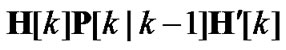 is used as a practically available approximation for the Cartesian position prediction’s error covariance.
is used as a practically available approximation for the Cartesian position prediction’s error covariance.
3. Debiased CMKF Performance Characteristics
This Section presents the results of a three-part investigation of the debiased CMKF’s performance in one simulated tracking scenario of [1]. For comparison purposes, we consider the four debiased-CMKF implementations summarized in Table 1. Debiased CMKF 1 is the ideal debiased CMKF which respectively uses 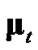 and
and 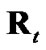 as the debiasing and covariance terms. Debiased CMKF 2 is the practical debiased CMKF which respectively uses
as the debiasing and covariance terms. Debiased CMKF 2 is the practical debiased CMKF which respectively uses 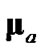 and
and —both of which are evaluated exclusively with the polar measurement—as the debiasing and covariance terms. Debiased CMKF 3 is the debiased CMKF of [1,2] which employs the test (11) to determine the polar estimate,
—both of which are evaluated exclusively with the polar measurement—as the debiasing and covariance terms. Debiased CMKF 3 is the debiased CMKF of [1,2] which employs the test (11) to determine the polar estimate, 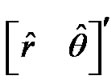 , with which to evaluate
, with which to evaluate 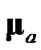 and
and 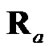 during tracking. Finally, debiased CMKF 4 is the debiased CMKF which exclusively uses the target’s true polar position,
during tracking. Finally, debiased CMKF 4 is the debiased CMKF which exclusively uses the target’s true polar position, 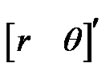 , to evaluate
, to evaluate 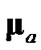 and
and  during tracking. Note that only the second and third considered debiased-CMKF implementations are practically realizable since the first and fourth implementations require the target’s true position.
during tracking. Note that only the second and third considered debiased-CMKF implementations are practically realizable since the first and fourth implementations require the target’s true position.
In all testing of the four debiased-CMKF implementations summarized in Table 1, we use the target-kinematics
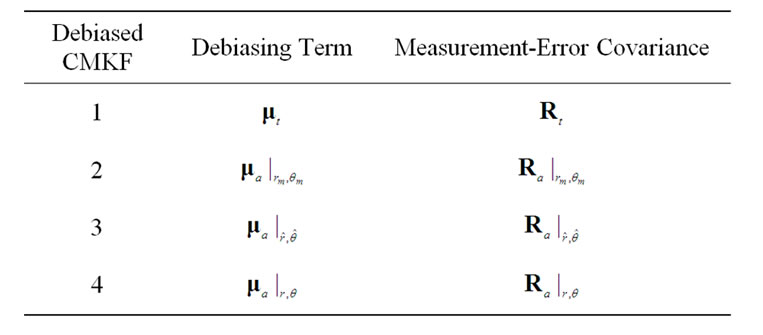
Table 1. Considered debiased-CMKF implementations.
model and the second test scenario (i.e., the case where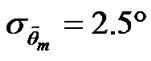 ) from the “Simulation Results” section of [1] (since the first test scenario yields qualitatively similar results). The presented results are those averaged over 100000 Monte-Carlo runs.
) from the “Simulation Results” section of [1] (since the first test scenario yields qualitatively similar results). The presented results are those averaged over 100000 Monte-Carlo runs.
3.1. Tracking Performance
Figure 1 shows the root-mean-squared (RMS) positiontracking errors of the four debiased-CMKF implementations specified in Table 1. With the exception of the first few measurement indices, the ideal debiased CMKF 1 yields the best tracking performance as expected. Consistent with the claim of [1], debiased CMKF 3 exhibits tracking performance superior to that of debiased CMKF 2. Debiased CMKF 4, which uses the best possible polar estimate, 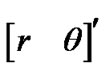 , to evaluate
, to evaluate 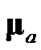 and
and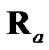 , nearly matches the performance of the ideal debiased CMKF 1 and in turn outperforms debiased CMKF 3 (after the first few measurement indices). Thus, these results support the tracking-performance claim made in [1] with regard to the use of better polar estimates for the evaluation of
, nearly matches the performance of the ideal debiased CMKF 1 and in turn outperforms debiased CMKF 3 (after the first few measurement indices). Thus, these results support the tracking-performance claim made in [1] with regard to the use of better polar estimates for the evaluation of 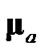 and
and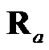 .
.
3.2. Statistical-Consistency Test
As stated earlier, in [1] Lerro and Bar-Shalom demonstrated that, for the static case in which  and
and  are evaluated exclusively with the polar measurement, the resulting
are evaluated exclusively with the polar measurement, the resulting 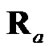 is statistically consistent with the actual debiased converted-measurement error for even fairly large bearing-measurement standard deviations (up to 10°). In addition, Lerro and Bar-Shalom showed the state-estimate error to be statistically consistent with the state-estimate-error covariance during tracking when using (11). However, no mention was made about the impact on the statistical consistency between the actual debiased converted-measurement error and
is statistically consistent with the actual debiased converted-measurement error for even fairly large bearing-measurement standard deviations (up to 10°). In addition, Lerro and Bar-Shalom showed the state-estimate error to be statistically consistent with the state-estimate-error covariance during tracking when using (11). However, no mention was made about the impact on the statistical consistency between the actual debiased converted-measurement error and 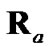 when both
when both 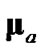 and
and 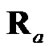 are evaluated with a polar estimate that is better than the polar measurement.
are evaluated with a polar estimate that is better than the polar measurement.
To quantify this effect, we use the statistical-consistency test outlined in Section III of [1] during tracking for the four previously specified debiased-CMKF implementations. Figure 2 shows the normalized error squared (NES) and the chi-square 0.99 probability bounds. Clearly, debiased CMKF 1 and debiased CMKF 2 both demonstrate the expected statistical consistency between their employed converted-measurement-error covariances and their respective actual debiased convertedmeasurement errors. Debiased CMKF 3 quickly loses statistical consistency between its 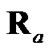 and its actual debiased converted-measurement error. Note that this loss of statistical consistency coincides exactly with the test (11) dictating the predicted polar estimate rather than the polar measurement be used to evaluate
and its actual debiased converted-measurement error. Note that this loss of statistical consistency coincides exactly with the test (11) dictating the predicted polar estimate rather than the polar measurement be used to evaluate 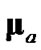 and
and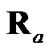 . Since
. Since 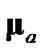 and
and 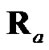 were originally derived from
were originally derived from 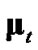 and
and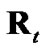 , respectively, by conditioning on the polar measurement, evaluating
, respectively, by conditioning on the polar measurement, evaluating 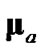 and
and 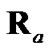 with a polar estimate having error statistics significantly different from those of the polar measurement compromises statistical consistency. For this same reason, debiased CMKF 4 never exhibits statistical consistency between its
with a polar estimate having error statistics significantly different from those of the polar measurement compromises statistical consistency. For this same reason, debiased CMKF 4 never exhibits statistical consistency between its 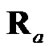 and its actual debiased converted-measurement error.
and its actual debiased converted-measurement error.
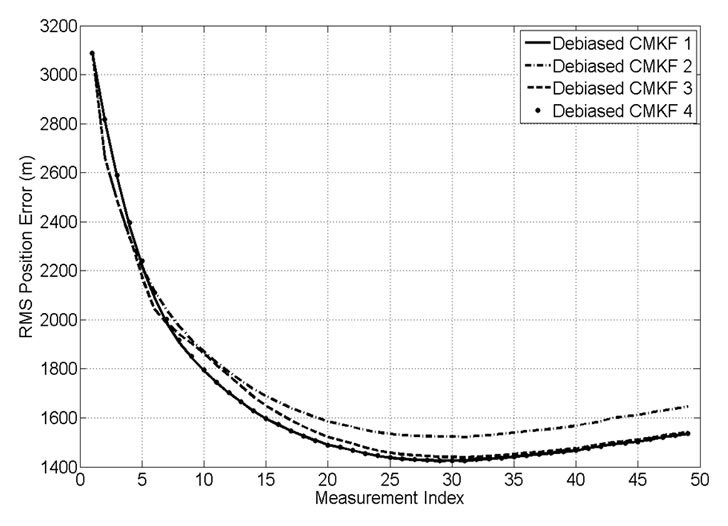
Figure 1. RMS position errors.
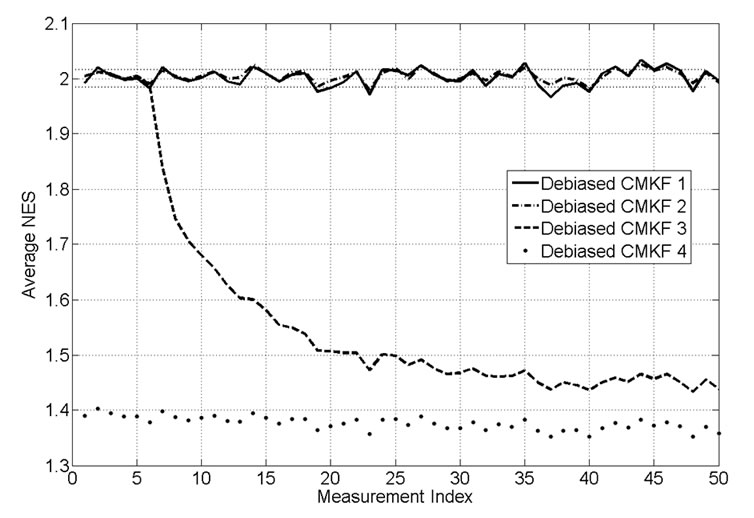
Figure 2. Average NES values.
3.3. Resolving the Apparent Contradiction
The four considered debiased-CMKF implementations of Table 1 are identical except for the employed debiasing terms and converted-measurement-error covariances. We thus postulate that debiased-CMKF implementations 3 and 4 achieve their superior tracking performance over debiased CMKF 2 because their employed debiasing terms and measurement-error covariances are “closer” to the respective “optimal” values. For the “optimal” debiasing terms and measurement-error covariances, we respectively propose 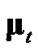 and
and  since using these ideal expressions ultimately yield the best debiasedCMKF tracking performance in simulation. We propose using
since using these ideal expressions ultimately yield the best debiasedCMKF tracking performance in simulation. We propose using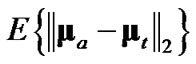 , the average 2-norm distance between each employed debiasing term and
, the average 2-norm distance between each employed debiasing term and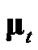 , as the metric for the employed debiasing term’s closeness to
, as the metric for the employed debiasing term’s closeness to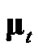 . Similarly, we propose using
. Similarly, we propose using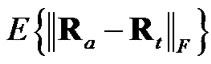 , the average Frobenius-norm distance between each employed measurement-error covariance and
, the average Frobenius-norm distance between each employed measurement-error covariance and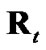 , as the metric for the employed measurement-error covariance’s closeness to
, as the metric for the employed measurement-error covariance’s closeness to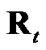 .
.
Figure 3 shows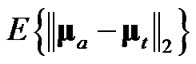 , obtained through simulation using a sample-mean approach, for the three non-ideal debiased-CMKF implementations specified in Table 1. While debiased CMKF 3 evaluates
, obtained through simulation using a sample-mean approach, for the three non-ideal debiased-CMKF implementations specified in Table 1. While debiased CMKF 3 evaluates 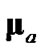 and
and 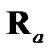 with the polar measurement, its
with the polar measurement, its 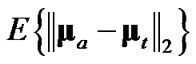 exactly equals the
exactly equals the 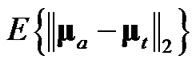 of debiased CMKF 2, as expected. However, as debiased CMKF 3 shifts to evaluating
of debiased CMKF 2, as expected. However, as debiased CMKF 3 shifts to evaluating 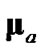 and
and 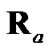 with the predicted polar estimate, its
with the predicted polar estimate, its 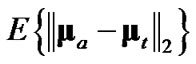 becomes smaller than the
becomes smaller than the 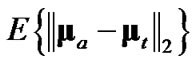 of debiased CMKF 2, indicating the
of debiased CMKF 2, indicating the 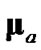 of debiased CMKF 3 is closer, on average, to
of debiased CMKF 3 is closer, on average, to 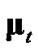 than is the
than is the 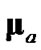 of debiased CMKF 2. By evaluating
of debiased CMKF 2. By evaluating 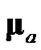 and
and 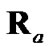 with the true position, debiased CMKF 4 achieves the smallest
with the true position, debiased CMKF 4 achieves the smallest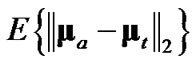 , indicating its debiasing term is the closest, on average, to
, indicating its debiasing term is the closest, on average, to 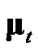 of all the considered non-ideal debiased-CMKF implementations.
of all the considered non-ideal debiased-CMKF implementations.
Figure 4 shows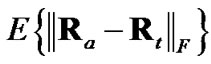 , obtained through simulation using a sample-mean approach, for the three non-ideal debiased-CMKF implementations specified in Table 1. While debiased CMKF 3 evaluates
, obtained through simulation using a sample-mean approach, for the three non-ideal debiased-CMKF implementations specified in Table 1. While debiased CMKF 3 evaluates 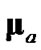 and
and 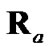 with the polar measurement, its
with the polar measurement, its 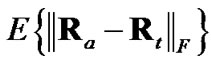 exactly equals the
exactly equals the 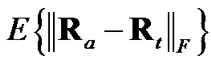 of debiased CMKF 2, as expected. However, as debiased CMKF 3 shifts to
of debiased CMKF 2, as expected. However, as debiased CMKF 3 shifts to
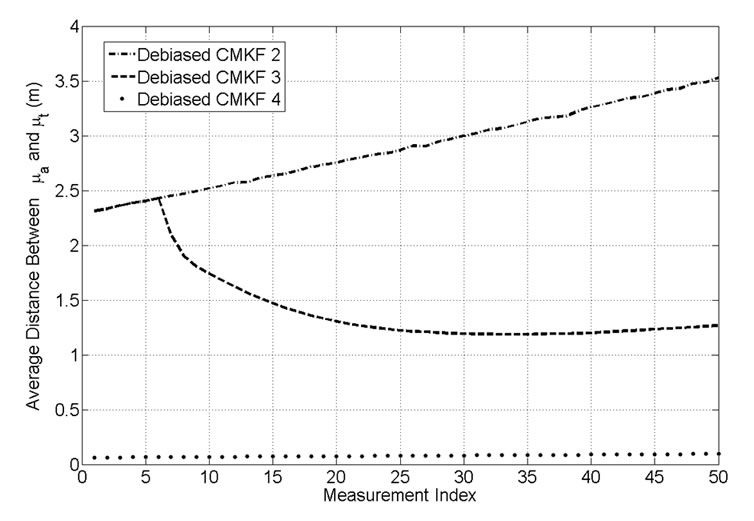
Figure 3. Average distance between the employed 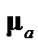 and
and .
.
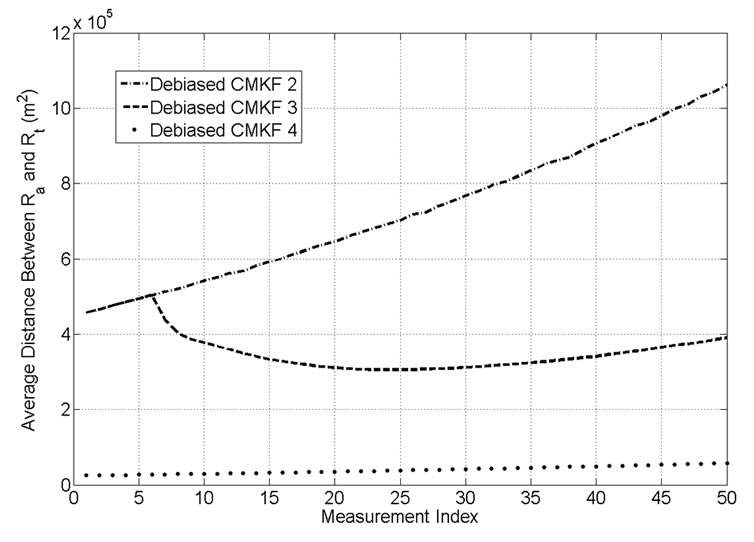
Figure 4. Average distance between the employed 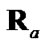 and
and .
.
evaluating  and
and 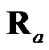 with the predicted polar estimate, its
with the predicted polar estimate, its  becomes smaller than the
becomes smaller than the 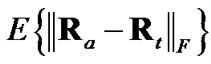 of debiased CMKF 2, indicating the
of debiased CMKF 2, indicating the 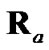 of debiased CMKF 3 is closer, on average, to
of debiased CMKF 3 is closer, on average, to 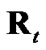 than is the
than is the 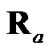 of debiased CMKF 2. By evaluating
of debiased CMKF 2. By evaluating 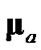 and
and 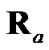 with the true polar position, debiased CMKF 4 achieves the smallest
with the true polar position, debiased CMKF 4 achieves the smallest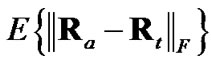 , indicating its measurement-error covariance is the closest, on average, to
, indicating its measurement-error covariance is the closest, on average, to 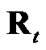 of all the considered non-ideal debiased-CMKF implementations.
of all the considered non-ideal debiased-CMKF implementations.
From Figures 3 and 4 it is apparent that the debiasedCMKF implementations which evaluate 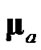 and
and 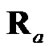 with polar estimates less uncertain than the polar measurements have both debiasing terms and convertedmeasurement-error covariances which are closer to the ideal
with polar estimates less uncertain than the polar measurements have both debiasing terms and convertedmeasurement-error covariances which are closer to the ideal 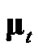 and
and , respectively.
, respectively.
4. Acknowledgements
J. N. Spitzmiller thanks Dr. D. Lerro for graciously making his computer programs available for review.
5. References
[1] D. Lerro and Y. Bar-Shalom, “Tracking with Debiased Consistent Converted Measurements Versus EKF,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 29, No. 3, 1993, pp. 1015-1022.
[2] D. T. Lerro, Alion Science and Technology, Private Communication, Mystic, CT, June 2008.
[3] D. T. Lerro, Alion Science and Technology, Private Communication, Mystic, CT, October 2008.
[4] X. R. Li and V. P. Jilkov, “A Survey of Maneuvering Target Tracking—Part III: Measurement Models,” Proceedings of SPIE Conference on Signal and Data Processing of Small Targets, San Diego, CA, USA, 2001, pp. 423-446.

