iBusiness
Vol.1 No.2(2009), Article ID:1052,7 pages DOI:10.4236/ib.2009.12013
Finding the Efficient Frontier for a Mixed Integer Portfolio Choice Problem Using a Multiobjective Algorithm
![]()
Democritus University of Thrace, Greece.
Email: kanagn@civil.duth.gr, gmamanis@pme.duth.gr
Received September 8, 2009; revised October 21, 2009; accepted November 29, 2009.
Keywords: Markowitz Model, Multiobjective Optimization, NSGA, Portfolio Selection
ABSTRACT
We propose a computational procedure to find the efficient frontier for the standard Markowitz mean-variance model with discrete variables. The integer constraints limit on the one hand the portfolio to contain a predetermined number of assets and, on the other hand, the proportion of the portfolio held in a given asset. We adapt the multiobjective algorithm NSGA for solving the problem. The algorithm ranks the solutions of each generation in layers based on Pareto non-domination. We have applied the procedure in sixty assets of ATHEX. We have also compared the algorithm with a single genetic algorithm. The computational results indicate that the procedure is promising for this class of problems.
1. Introduction
Every investor faces the problem of choice the appropriate assets in which he will invest his funds. To support such decisions, H. M. Markowitz set up some fifty years ago a quantitative framework, in which the selected portfolio is optimum with respect to both the expected return and the variance of return and maximizes the so-called utility function [1,2]. The optimal portfolio offers the highest level of expected return for a given level of risk and the minimum level of risk for a given level of return. All such portfolios are called efficient and constitute the efficient frontier. The assumption that asset returns follow the normal distribution allows the finding of efficient frontier via quadratic programming.
However, Markowitz mean-variance model has been criticised not only for the main assumptions it is based upon, but also because it neglects some important aspects of portfolio performance in real life situations. As a result, some other measures of risk have been used, e.g. Value-at-Risk [3,4]; and additional constraints were introduced in the standard model in order, for example, to avoid very small holdings, to restrict the total number of holdings and/or to take into consideration the roundlot of assets that can be bought or sold in a bunch [5].
Since these additional constraints lead to sets of discrete variables and constraints, the resulting optimization problem becomes quite complex as it exhibits multiple local extrema and discontinuities [4,6–8]. In such situations, especially in large-scale instances of the problem, classical optimization methods do not work efficiently and heuristic optimization techniques are the only alternatives for finding optimal or near-optimal solutions in a reasonable amount of time. Thus, researchers have experimented with the application of heuristic optimization techniques for finding the efficient frontier of the standard Markowitz model enriched with practical constraints. However, it must be noted that, although many metaheuristic algorithms have been developed in the past [9], “few authors seem to have investigated the application of local search metaheuristics for solving the portfolio selection problems” [7].
One of the first attempts for the use of heuristic optimization techniques to portfolio selection was made by Mansini and Speranza [10]. They have formulated the optimum portfolio choice with round lots as a mixed integer programming problem and they have proposed heuristics for its solution based upon the idea of constructing and solving mixed integer sub-problems, which consider subsets of the available investment choices. Chang et al. [6] have extended the standard Markowitz model to include cardinality constraints as well as upper and lower bounds on the proportion of the portfolio invested in each asset. For finding the cardinality constrained efficient frontier the authors have applied three heuristic algorithms based upon genetic algorithms, tabu search and simulated annealing. For the same problem, Anagnostopoulos et al. [11] have also proposed a GRASP algorithm enhanced by a learning mechanism and a bias function for determining the next element to be introduced in the solution. Crama and Schyns [7] have also applied a simulated annealing algorithm but they have extended the model to contain not only cardinality constraints and upper and lower bounds, but also trading and turnover constraints. Jobst et al. [8] investigated the shape of the efficient frontier of the mean-variance model including buy-in thresholds, cardinality constraints and round lot restrictions using a branch-and-bound algorithm combined with heuristics.
In any case, the construction of the efficient frontier via quadratic programming requires the optimization problem to be solved several times for various values of return. In this paper we confront the standard Markowitz model with cardinality constraints as a bi-objective optimization problem in order to find the efficient frontier in a single execution of the algorithm. The problem is solved by a multiobjective genetic algorithm, which uses a non-dominated sorting procedure to select the best parents. To the best of our knowledge, a few of the related studies in the literature use a proper multiobjective algorithm to construct the Pareto front within the context of a portfolio selection problem such as the one considered in this work. The algorithm was applied in 60 assets of ATHEX and a comparison with a variant of the single (as opposed to multiobjective) genetic algorithm, which has been proposed by Chang et al. [6], was realized. The computational results indicate that the procedure is very promising for this class of problems.
The rest of this paper is organized as follows. In Section 2, after a short review of the Markowitz model, the portfolio selection is defined as a multiobjective combinatorial problem. An adaptation of the Nondominated Genetic Algorithm (NSGA) for solving the problem is presented in Section 3. Section 4 is devoted to our numerical results, and some concluding remarks are presented in Section 5.
2. T he Formulation of the Problem
2.1 The Markowitz Mean-Variance Model
The problem of optimally selecting a portfolio among N assets was formulated by H.M. Markowitz in 1952. H. M. Markowitz based on the assumption that every investor has the desire to achieve a predetermined return and to minimize risk on investment. Mean or expected return is employed as a measure of return and standard deviation or variance of return is employed as a measure of risk. Among all portfolios there are special ones for which it cannot be said that one is better than the other. All such portfolios that are Pareto-optimal (or non-dominated) offer the maximum level of return for a given level of risk, or equivalently, the minimum level of risk for a given level of return. The investor should select a portfolio among the efficient portfolios. The proper choice among efficient portfolios depends on the willingness and ability of the investor to assume risk.
However, the main problem is to find this efficient frontier. Under the assumption of the normality of returns, this can be done by solving a quadratic optimization problem for all possible values of ρ, i.e. the desired level of return. The set of all optimal solutions constitutes the mean-variance frontier. It is usually displayed as a curve in the plane where the vertical axis denotes portfolio’s expected return, while the horizontal axis represents the variance of this return. Mathematically, the problem can be formulated as follows:
min  (1)
(1)
subject to
 (2)
(2)
 (3)
(3)
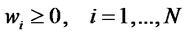 (4)
(4)
where:
 : the decision variable which denotes the proportion held of asset i
: the decision variable which denotes the proportion held of asset i
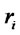 : the expected return of asset i
: the expected return of asset i
 : the covariance between assets i and j
: the covariance between assets i and j
 : the desired level of return
: the desired level of return
 : the number of assets available The objective function (1) minimizes the total variance (risk) associated with the portfolio, while Equation (2) ensures that the portfolio has an expected return of ρ. Equations (3) and (4) describe budget and non-negativity constraints respectively. Budget constraint ensures that 100% of the budget is invested in the portfolio, while non-negativity constraints ensure that no asset has a negative proportion.
: the number of assets available The objective function (1) minimizes the total variance (risk) associated with the portfolio, while Equation (2) ensures that the portfolio has an expected return of ρ. Equations (3) and (4) describe budget and non-negativity constraints respectively. Budget constraint ensures that 100% of the budget is invested in the portfolio, while non-negativity constraints ensure that no asset has a negative proportion.
An alternative form of the model is often used in practice (see, for example, [6,11] by removing the return constraint and replacing the objective Function (1) by
 (5)
(5)
Values of λ satisfying 0 lb λ lb 1 represent an explicit tradeoff between risk and return, and generate solutions between the two extremes λ = 0 and λ = 1. To draw the efficient frontier, the problem is repeatedly solved using several values of λ.
2.2 The Multiobjective Optimization Model
For more realistic portfolio selection several extensions of Markowitz standard model have been proposed. In real financial decision-making, it is useful to avoid very small holdings, and to restrict the total number of assets. These requirements can be modeled as threshold and cardinality constraints. In general, both lead to sets of discrete variables and constraints.
Threshold and cardinality constraints can be added to the model using a binary variable zi, which is equal to 1 if the asset i (1lbilbN) is held in the portfolio and 0 otherwise. Introducing finite upper and lower bounds εi, δi for the stock weight wi, threshold constraints are represented by the following inequality:

To facilitate portfolio management or to control transaction costs, some investors may wish to limit the number of assets held in their portfolio. The cardinality constraint, which limits the portfolio to contain predetermined number of assets K, can be added to the model by counting the binary variables zi. This constraint is expressed by the following equation:
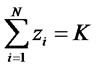
When such constraints are added, the resulting mixed integer program becomes larger in size and computationally more complex than the standard mean-variance model.
In this paper we reformulate the quadratic optimization problem into a two-objective optimization problem. This allows us to find the efficient frontier in a single execution of the algorithm. The vector objective function has as elements the portfolio return and the variance of return. Moreover our model has been enriched with threshold and cardinality constraints.
The problem to be solved is formulated as follows:
opt 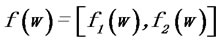
subject to


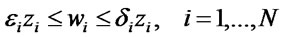
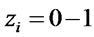
The objective function represents portfolio’s return while the objective function
represents portfolio’s return while the objective function  represents portfolio’s variance of return. The N-vector w denotes the set of decision variables wi.
represents portfolio’s variance of return. The N-vector w denotes the set of decision variables wi.
3. The Multiobjective Algorithm
Multiobjective genetic algorithms have gained much attention last years in solving optimization problems with multiple objectives [12,13]. The primary reason of these studies is the unique feature of genetic algorithms to use a population of solutions. This allows multiple Paretooptimal solutions to be found in a single simulation run. It appears that the first who tried to use genetic algorithms for finding the Pareto frontier in a multiobjective optimization problem was Schaffer [14]. Although his Vector Evaluated Genetic Algorithm (VEGA) gave encouraging results, it suffered from biasness towards some Pareto-optimal solutions. To overcome this problem, it is suggested the use of both techniques, a nondominated sorting procedure to move a population toward the Pareto front and some kind of niching technique to keep the GA from converging to a single point on the front. Based on this suggestion a number of independent GA implementations have been proposed, for example the MultiObjective Genetic Algorithm (MOGA) [15] and the Niched-Pareto Genetic Algorithm (NPGA) [16].
Srinivas and Deb [17] proposed the Nondominated Genetic Algorithm (NSGA) which is based on several layers of classifications of individuals. Before selection, a procedure ranks the solutions of each generation in layers based on Pareto non-domination. Firstly, the nondominated individuals are identified so that to constitute the first nondominated front; and they are assigned a large dummy fitness value, which is proportional to population size, to provide an equal reproductive potential to all these nondominated individuals. To maintain diversity in the population classified individuals are shared with their dummy fitness values. Sharing is achieved by dividing each individual’s dummy fitness value by a niche count which is proportional to the number of individuals one has in its neighborhood. The parameter niche count for every individual i in the front is calculated by the following equation:
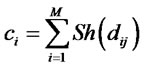
where Sh(dij) is the sharing function, dij is the phenotypic distance between individuals i and j, and M is the number of individuals in the current front. Sharing function is expressed by the equation

where usually α = 1, and σsh is the maximum distance allowed between two individuals.
Sharing function plays an important role in NSGA’s performance, and it is strongly depended on the appropriate selection of the parameter σsh. The method proposed by Deb and Goldberg for estimating σsh seems do not to work efficiently in our problem. This is probably due to the additional integer constraints which limit the search space. Thus, the algorithm was executed several times for different values of the parameter σsh, which was kept smaller than the initial value computed by Deb and Goldberg’s method, until the best efficient frontier was found. After sharing, these individuals are ignored temporarily and the second front of nondominated individuals is identified. These new set of points are assigned a new dummy fitness value which is kept smaller than the minimum shared fitness value of the first front (95% of the smallest shared fitness value of the previous front). The process continues until all individuals in the population are classified.
The population is then reproduced according to the shared fitness value. A stochastic remainder proportionate selection is used in this approach. Since individuals in the first front have the maximum fitness value, they always get more copies than the rest of the population. This allows the search for nondominated regions and sharing helps to distribute the population over this region. The efficiency of NSGA lies in the way multiple objectives are reduced to a dummy fitness function using nondominated sorting procedure. Another aspect is that any number of objectives can be solved and both minimization and maximization problems can be handled [17]. The pseudocode of the algorithm is shown in Figure 1.
A crucial aspect in genetic algorithms is how to represent a solution. The chromosome is divided into two parts. The first part is a set A of K distinct assets and the second one is a set B that includes K real numbers associated with each asset i.


Then, in order to find the proportion of each asset, the free portfolio proportion is calculated as follows

Thereafter, the proportion associated with each asset in the portfolio is calculated by the following equation

In this way all the constraints are satisfied.
The offspring are generated by uniform crossover as described below. If an asset is present in both parents it is present in the children with the corresponding associated value n. The remaining non-common assets are then selected randomly to fulfill children’s sets. An example can be seen in Table 1.

Table 1. Crossover example
Children are also subject to mutation by multiplying by 0.9 or 1.1 (chosen with equal probability) the value ni of a randomly selected asset i. The next generation of individuals completely replaces the current population.
4. Computational Results
The algorithm has been implemented in Visual Basic and run on a personal computer Pentium 4 at 2.4 GHz. To construct the data set, 60 assets of big και medium capitalization from Athens Exchange were considered and weekly prices from 10-5-2005 to 12-5-2006 were used to calculate returns and covariances. The weekly
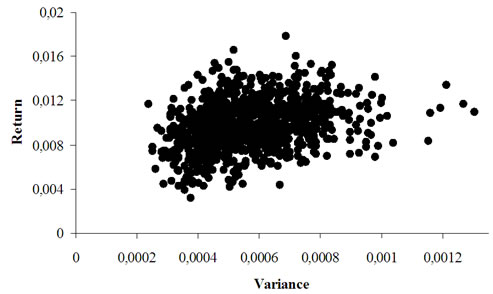
Figure 2. The initial population

Figure 3. The efficient frontier, K = 10
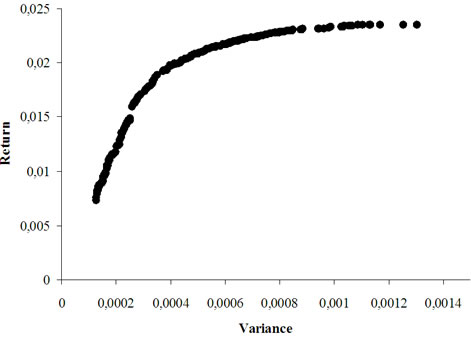
Figure 4. The efficient frontier, K = 5
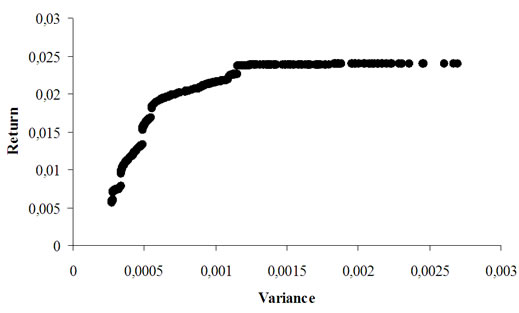
Figure 5. The efficient frontier, K = 2

Table 2. Parameters of the problem
return 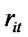 of the asset i in the period t was calculated according the equation
of the asset i in the period t was calculated according the equation
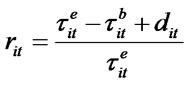
where 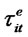 (
( ) is the closing price of asset i at the end (beginning) of period t and
) is the closing price of asset i at the end (beginning) of period t and  is the dividend paid to shareholders in period t.
is the dividend paid to shareholders in period t.
We tried to find the efficient frontier for different values of K and especially for K = 2, 5, 10. For all these problems lower and upper bounds were 1% and 100% respectively, i.e., .
.
In order to see the algorithm performance, an initial population has been randomly generated (Figure 1). Figures 2, 3 and 4 represent the cardinality constrained efficient frontier for K = 2, 5, 10 respectively. As we can see from these outputs, the algorithm has found many Pareto-optimal points with good distribution along the efficient frontier. The number of generated points and their distribution are crucial aspects in multiobjective optimization.
If the multiobjective algorithm converges in a small region near or on the true Pareto-optimal front, the purpose of multiobjective optimization is not served. This is because, in such cases, many interesting solutions with large trade-offs among the objectives and parameter values have been probably undiscovered. Table 1 illustrates this distribution of points for each problem instance, together with important parameters of the algorithm.
We have also implemented a variant of the genetic algorithm proposed in [6]. The differences between their genetic algorithm and our algorithm are, on the one hand, the complete replacing of the solutions (as in our multiobjective algorithm) versus the partial replacing and, on the other hand, the rank selection versus the tournament selection. Because of limited space, only some of the obtained results are presented.
In order to compare the quality of solutions obtained by the multiobjective genetic algorithm and the single objective genetic algorithm, we use the technique proposed in [18]. The multiobjective genetic algorithm is considered not worse than the single objective if

where sl is the scalarizing function, wsl the best solution obtained by optimization of sl with the single GA and wml the best solution on sl selected from the set of Paretooptimal solutions generated by the multiple objective GA.
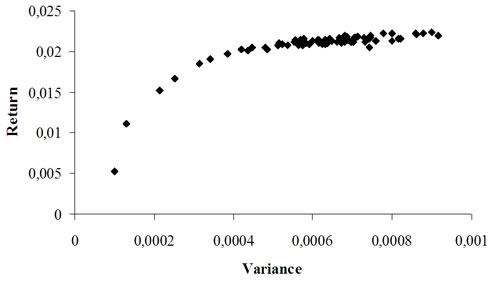
Figure 6. The efficient frontier generated by the single genetic algorithm, K = 10.
Figure 6 shows the solutions obtained by optimizing 81 objective functions (l = 1,…, 81) with single objective GA, defined for values λ = 0 to 1 with step 0.0125 (see Equation (5)). Since
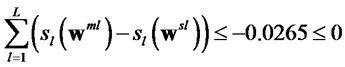
we may compare the computational requirements of the two approaches. The effectiveness index is equal to

where CTs is the average running time the single objective GA spent on optimization of sl and CTm the running time the multiobjective GA needs to generate the Paretooptimal solutions s1…sL. These results are based on the Pareto front generated from the multiobjective algorithm with 200 generations. If the generations are equal to 50 (although the Pareto front is slightly inferior), the equation is still verified and the EI is equal to 6,025. Thus we can conclude that the generation of the Pareto-optimal solutions with NSGA is competitive both from the computational effectiveness point of view and the quality of the Pareto front.
5. Conclusions
Constraints in the size of the portfolio and in lower and upper bounds on the proportion of the portfolio held in a given asset transform the standard Markowitz model in a mixed integer optimization problem and create discontinuities in the efficient frontier. In this paper we adapt the multiobjective algorithm NSGA for finding the cardinality constrained efficient frontier.
We argue that the proposed procedure solves efficiently the cardinality constrained portfolio optimization problem as it generates in relatively short computational time a large number of Pareto-optimal solutions, which are uniformly distributed along the efficient frontier. Even if the efficient frontier is not continuous and, then, competition among solutions may lead to extinction of some sub-regions, the algorithm finds a large number of Pareto-optimal solutions in every segment. On the other hand, the procedure is in general time consuming, since the quality of solutions depends on the population size, but this shortcoming is balanced by the fact that the efficient solutions are obtained after a small number of generations. Finally, a further difficulty is the appropriate selection of σsh as the algorithm performance is highly dependent on this value.
Constraints in the size of portfolio and in lower and upper bounds on the proportion of the portfolio in a given asset help the decision maker to facilitate its portfolio management; and to avoid excessive transaction costs on one hand, and to avoid holding very small/large amounts of any particular asset on the other. It is empirically known that much of the portfolio risk can be diversified by holding a rather small number of assets [4,19]. We have solved for the efficient frontier following the tradition of standard Markowitz approach, however, focusing on the case where the investor wants to invest in exactly K out of N number of assets. Furthermore, portfolios with positions in assets with very small amounts have been excluded through the use of threshold constraints. The resulting efficient frontier gives the best possible trade-off of risk against return for a particular number of assets (K). The investor then examines the trade-off points in the possibilities curve and selects the one particular point of interest. This may be the point with the lowest variance but having the lowest return, located in the lower left part of the frontier; or it may be the point with the maximum expected return but with the maximum risk, located in the right upper part of the frontier; or it may be any intermediate point. The proper selection of the particular point depends on the investor’s willingness to assume risk. In the next step, the investor implements the one particular portfolio whose image is the point in the nondominated frontier. Furthermore, solving for different values of K, the trade-off between risk, return and the number of assets of the portfolio could be examined.
Currently our research focus on a generalization of the cardinality constrained mean-variance problem, by including class constraints that limit the proportion of the portfolio that can be invested in assets in each class, such as bank stocks, telecommunication stocks etc. For its solution, procedures of the so called second generation multiobjective genetic algorithms are tested.
REFERENCES
- Markowitz, H. M., “Portfolio selection,” Journal of Finance, No. 7, pp. 77–91, 1952.
- Markowitz, H. M., “Portfolio selection, efficient diversification of investments,” Blackwell, Cambridge MA and Oxford UK, 1990.
- Benati, S. and Rizzi, R., “A mixed integer linear programming formulation of the optimal mean/value-at-risk portfolio problem,” European Journal of Operational Research, Vol. 176, No. 1, pp. 423–434, 2007.
- Gilli, M. and K"ellezi, E., “A global optimization heuristic for portfolio choice with VaR and expected shortfall,” in Kontoghiorghes, E. J., Rustem, B., and Siokos, S., Eds., Computational Methods in Decision-Making, Economics and Finance, Applied Optimization Series, Kluwer Academic Publishers, pp. 167–183, 2002.
- Mitra, G., “A review of portfolio planning: Models and systems,” in Satchell, S., Scowcroft, A., Eds., Advances in Portfolio Construction and Implementation, Butterworth-Heinemann, Amsterdam, pp. 1–39, 2003.
- Chang, T. J., Meade, N., Beasley, J. E., and Sharaiha, Y. M., “Heuristics for cardinality constrained portfolio optimization,” Computers & Operations Research, 27, pp. 1271–1302, 2000.
- Crama, Y. and Schyns, M., “Simulated annealing for complex portfolio selection problems,” European Journal of Operational Research, No. 150, pp. 546–571, 2003.
- Jobst, N. J., Horniman, M. D., Lucas, C. A., and Mitra, G., “Computational aspects of alternative portfolio selection models in the presence of discrete asset choice constraints,” Quantitative Finance, Vol. 1, pp. 1–13, 2001.
- Blum, C. and Roli, A., “Metaheuristics in combinatorial optimization: Overview and conceptual comparison,” ACM Computing Surveys, Vol. 35, No 3, pp. 268–308, 2003.
- Mansini, R. and Speranza, M. G., “Heuristic algorithms for the portfolio selection problem with minimum transaction lots,” European Journal of Operational Research, Vol. 114, No. 2, pp. 219–233, 1999.
- Anagnostopoulos, K. P., Chatzoglou, P. D., and Katsavounis, S., “A reactive greedy randomized adaptive search procedure for a mixed integer portfolio optimization problem,” in P.D. Chatzoglou, Ed., Proceedings of the 2nd International Conference on Accounting and Finance in Transition (CD), 2004.
- Coello, C. A., “An updated survey of GA-based multiobjective optimization techniques,” ACM Computing Surveys, Vol. 32, No 2, pp. 109–143, 2000.
- Deb, K., “Multiobjective genetic algorithms: Problem difficulties and construction of test problems,” Evolutionary Computation, Vol. 7, No. 3, pp. 205–230, 1999.
- Schaffer, J. D., “Multiple objective optimization with vector evaluated genetic algorithms,” in Grefenstette, J. J., Ed., Proceedings of the First International Conference on Genetic Algorithms and Their Applications, Lawrence Erlbaum, Hillsdale, New Jersey, pp. 93–100, 1985.
- Fonseca, C. M., and Fleming, P. J., “Genetic algorithms for multiobjective optimization: Formulation, discussion, and generalization,” in Forrest, S., Ed., Proceedings of the Fifth International Conference on Genetic Algorithms, Morgan Kaufmann, San Mateo, California, pp. 416–423, 1993.
- Horn, J., Nafpliotis, N., and Goldberg, G. E., “A niched Pareto genetic algorithm for multiobjective optimization, Piscataway,” IEEE Service Center, NJ, pp. 82–87, 1994.
- Srinivas, N. and Deb, K., “Multiobjective optimization using nondominated sorting in genetic algorithms,” Evolutionary Computation, Vol. 2, No. 3, pp. 221–248, 1994.
- Jaszkiewicz, A., “On the computational effectiveness of multiple objective metaheuristics,” in Proceedings of the Fourth International Conference on Multi-Objective Programming and Goal Programming MOPGP'00, Theory & Applications, Berlin-Heidelberg, Springer–Verlag, May 29–June 1, 2000.
- Maringer, D., “Portfolio management with heuristic optimization,” Springer, New York, 2005.


