Positioning
Vol.2 No.1(2011), Article ID:3900,4 pages DOI:10.4236/pos.2011.21006
Information Method for Synthesis of Optimal Data Subsystems Designated for Positioning, Location and Remote Sensing Systems
![]()
1Research Institute of Aerospace Informatics, Baku, Azerbaijan; 2National Aviation Academy, Baku, Azerbaijan.
Email: Hasadzade2001@yahoo.com
Received December 22nd, 2010; revised January 14th, 2011; accepted January 28th, 2011.
Keywords: Synthesis, Subsystems, Optimization, Remote sensing, Positioning, Location
ABSTRACT
The general classification of information systems of remote action, including such system as positioning systems, location systems and remote sensing systems is suggested. In view of formulated limitation conditions the common mathematical information model of data transfer subsystems of considered systems is suggested. The optimization of developed information model is carried out and the optimal operation regimes of these data transfer subsystems are synthesized.
1. Introduction
There are different types of information measuring systems, the operations of which are carried out using noncontact methods, from remote or stand-off positions. In these systems transfer of initial measuring information is carried out using different physical waves, such as electromagnetic, acoustic, gravitation ones. In this article we shall consider from common positions the data transfer subsystems designated for systems of remote action (RAS), i.e. such type of systems, which carry out one of following types of remote operations:
1) Remote sensing;
2) Location;
3) Positioning.
The above said remote operations are determined as follows:
1) Remote sensing systems carry out remote (standoff) measurements using physical waves to produce and transfer measuring data;
2) Location systems carry out localization of the object, which emits any type of physical waves, carrying information about geometric or geographic positions of the object;
3) Positioning systems carry out determination of its geometric or geographic position on the basis of measuring information on coordinates sent by several remote objects using physical waves.
In present article we shall describe the proposed table classification of data transfer subsystems, develop the universal information model of these subsystems, and carrying out optimization of the model we shall perform the synthesis of optimal operation regimes of them.
In previous our published papers [1-6] the similar approach was suggested, but generalization of this method for all data transfer subsystems designated for Remote action systems was not done.
2. Information Models of Data Transfer Subsystems
First of all we should develop the information models of above said types of subsystems. We shall use the common limitation condition for these subsystems, develop the generalized model of all three types of them and then carrying out optimization of this model we shall succeed synthesis of optimal operation regimes of data transfer.
The model of data transfer subsystems of positioning system is shown in Figure 1.
In this model (Figure 1) the receiver, located on the object О receives information about geometric or geographic coordinates of points “Transmitter 1”, “Transmitter 2”, “Transmitter 3” and analyzing that transfers it for further processing to determine its own geometric or geographic coordinates.
The model of the location system is shown in Figure 2. In this model the receivers, located on the objects О1, О2 and О3 receive the potential information on geographic coordinates of point P and transfer it for further processing to determine its location coordinates.
Models of data transfer subsystem designated for remote sensing systems are shown in Figures 3(а), (b).
In the first model (Figure 3(а)) the information coming from objects О1, О2 and О3 is received by single Receiver (sensor). In the second model (Figure 3(b)) the information coming from the object О is received by all Receivers, i.e. the group sensing is carried out.
The aim of remote sensing systems is to receive the maximum amount of information coming from studied objects.
The suggested general classification scheme of abovementioned types of remote action systems is given in the Table 1.
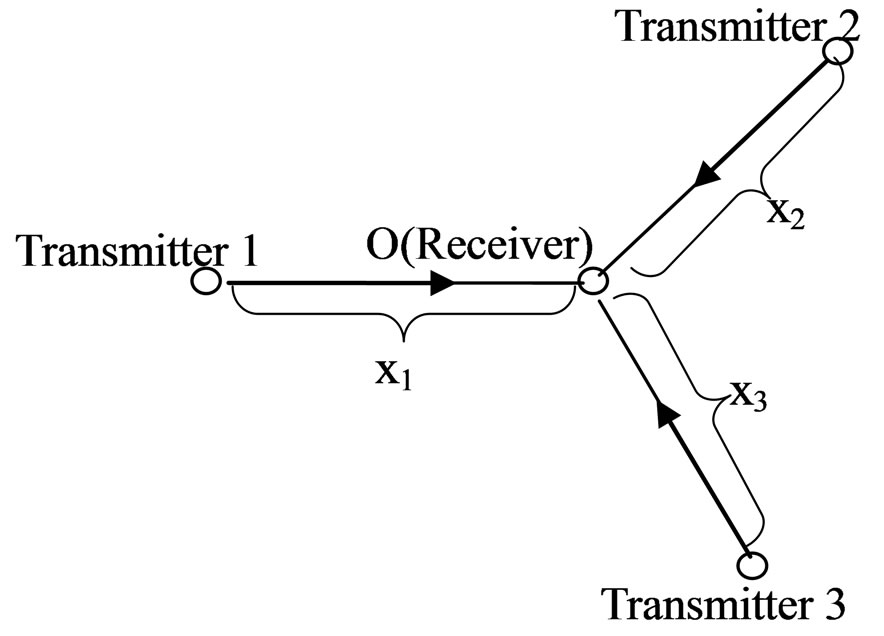
Figure 1. Model of data transfer subsystems of positioning system.
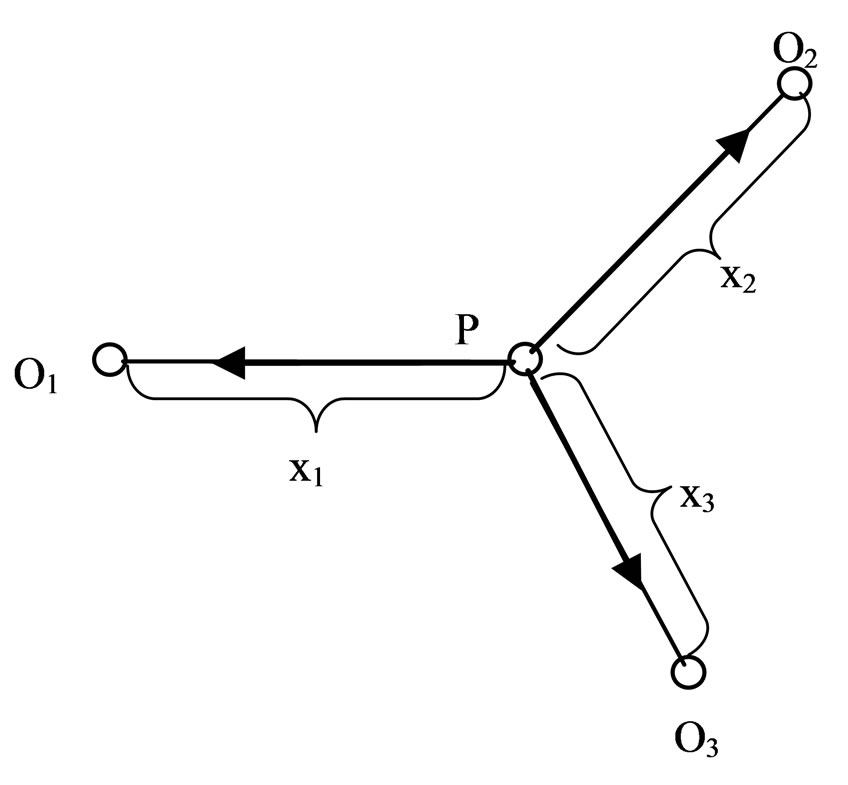
Figure 2. Model of data transfer subsystem designated for location system.
 (a)
(a)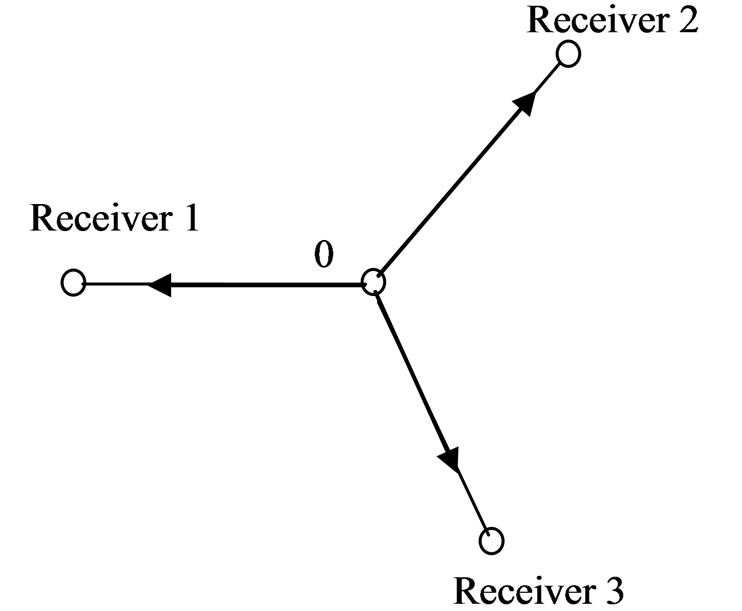 (b)
(b)
Figure 3. Models of data transfer subsystem designated for remote sensing systems.

Table 1. Classification scheme of remote action systems.
3. Optimization of Operation of Data Transfer Subsystems
On the basis of suggested classification scheme we shall develop the general mathematical model of data transfer subsystems for considered types of remote action systems. Then we shall optimize the optimal operation regime of said types of subsystems.
In order to develop the general information-mathematic model we accept following major limitation conditions:
1). General limitation condition concerning sum of distances xi, which should be constant, i.e.
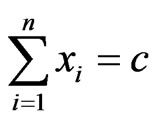 (1)
(1)
Obviously, that if the speed of propagation of waves in the channels is constant, the condition (1) may be rewritten as
 , (2)
, (2)
where 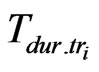 – duration of transmission of the signal via i-th channel.
– duration of transmission of the signal via i-th channel.
2). Presence of effect of signal’s energy attenuation in channels. Concerning this effect we assume, that the total attenuation of the signal is proportional to the length of used channel.
In view of above said basic conditions, the common information target functional may be written as
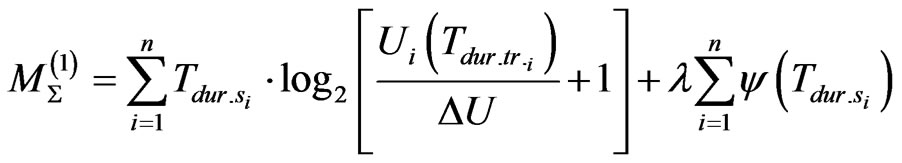 , (3)
, (3)
where λ – multiplier of L’Agrange; ΔU – total noises in the system;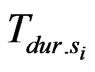 – duration of the signal transferred via i-th channel.
– duration of the signal transferred via i-th channel.
Optimization of the common model (3) will be carried out using variation computation method. We should find out such a function.
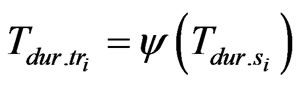 , (4)
, (4)
upon which the functional (3) will reach it own maximal value.
In view of (4), the functional (3) may be rewritten as follows
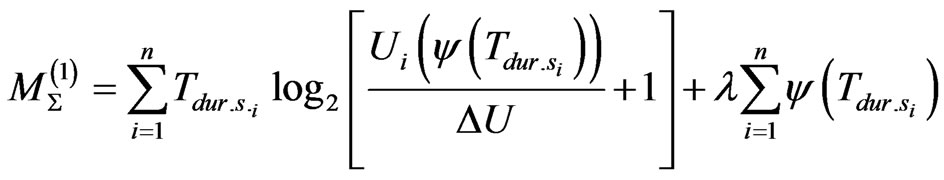 .(5)
.(5)
Taking into account that ΔU denotes the noises of measurements the ratio 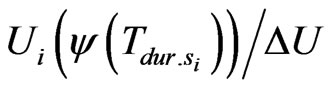 will indicate the signal/noise ratio. Let us consider the function
will indicate the signal/noise ratio. Let us consider the function
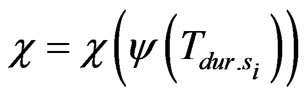 (6)
(6)
Taking into consideration the function (6), the Equation (5) may be written in the following analogue form
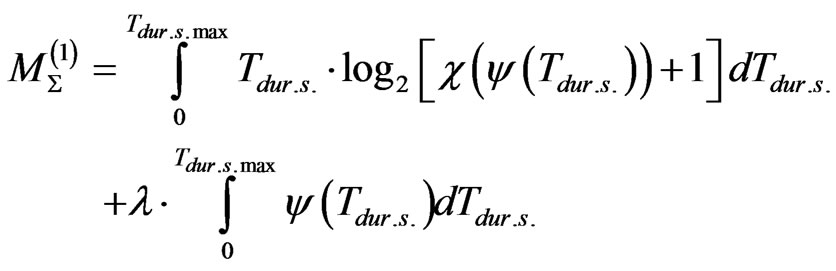 (7)
(7)
The condition (4) may be written in the following analogue form
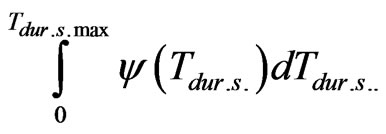 = с1 = const.(8)
= с1 = const.(8)
The function 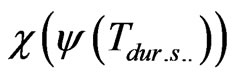 may be submitted as
may be submitted as
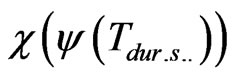 = cо+c‘∙y
= cо+c‘∙y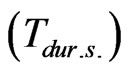 (9)
(9)
Taking into account the Formula (9) the functional (7) may be written as
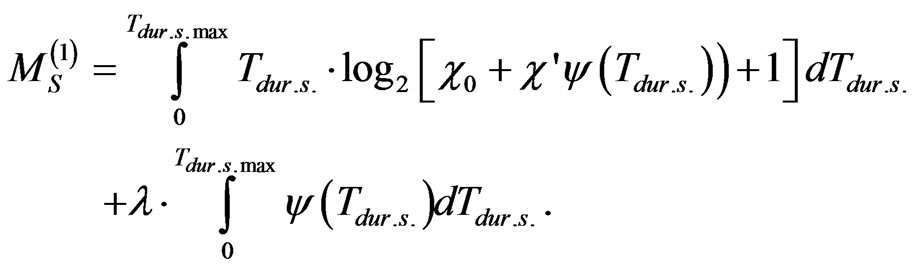 (10)
(10)
In this case the analogue of the function (4) may be written as
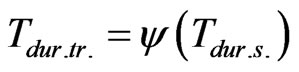 (11)
(11)
Let us to find the function (11), upon which the functional (10) could reach its maximal value.
In order to solve this task we use Euler’s method. Application of this method to Equation (10) gives us following formula
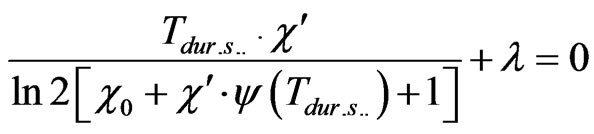 . (12)
. (12)
From (12) we can find following function
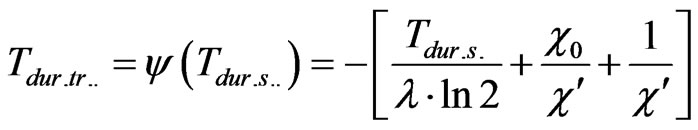 (13)
(13)
Taking into consideration (13) in Formula (8) we get
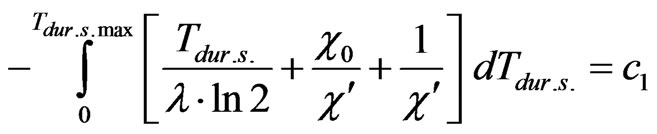 . (14)
. (14)
From Formula (14) we find
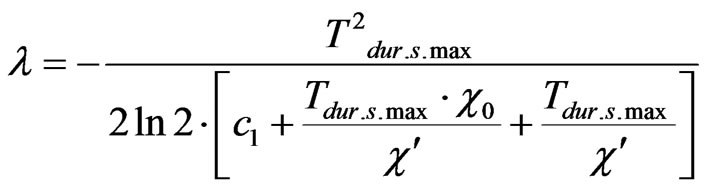 (15)
(15)
Taking into consideration Formulas (15) and (12) we can obtain following result
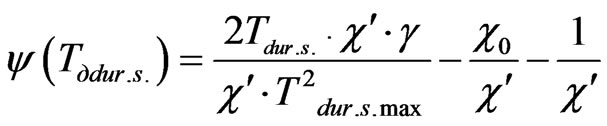 , (16)
, (16)
where 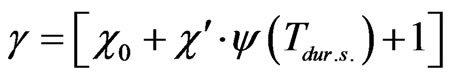
In view of negative value of c in formula (16) we obtain following final result
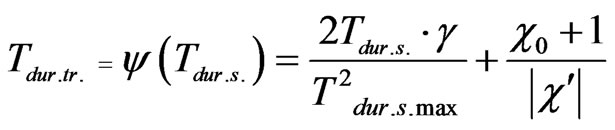 . (17)
. (17)
As it is clear from formula (17) if the parameter g has a negative value, the parameter  will be in inverse dependence from Тdur.s. and vice versa.
will be in inverse dependence from Тdur.s. and vice versa.
The unimodality of the functional (10) may be checked by calculation the second derivative of Equation (10) on y. It is easy to show, that the value of the second derivative is always negative.
4. Formulation of Suggested Method for Synthesis of Optimal Data Transfer Subsystems
Taking into consideration all above said we can suggest the following method for synthesis of optimal data transfer subsystems for positioning and location systems:
1) The following set is to be composed {Тdur.s.1, Тdur.s.2, Тdur.s.3}.
2) The rotation of elements of composed set should be carried out on transmitters.
3) The value of the functional (10) should be calculated.
4) The process of rotation should be stopped when the functional (10) reaches its maximal value.
5) Duration of transfer of signals via channels is to be calculated using formula (17).
6) Calculation of distances between transmitters and receivers make it possible to carry out both the positioning and location.
The suggested method for synthesis of optimal data transfer subsystems for remote sensing is following:
1) We should compose the set {Тdur. s.1, Тdur. s.2, Тdur. s.3}.
2) Upon known lengths of channels, known values of parameters g, c’, co and , using the formula (17) we should carry out distribution and rotation of elements of above set on channels.
, using the formula (17) we should carry out distribution and rotation of elements of above set on channels.
3) The maximal value of information, which could be obtained as a preliminary result of remote sensing, should be calculated using Formulas (10) and (17).
5. Conclusions
In conclusion following major results of held research may be formulated. We suggest the universal classification of information systems of remote action, which includes the positioning, location and remote sensing systems.
The common mathematical-information model of the data transfer subsystems of abovementioned systems is suggested. The variation optimization of the developed model is carried out taking into account the formulated limitation condition.
Optimization of data transfer subsystems information model makes it possible to synthesize the optimal operation regimes of mentioned subsystems designated for positioning, location and remote sensing systems.
6. Acknowledgements
Authors are deeply grateful to academician A. Sh. Mehdiyev for his valuable support rendered during their research work related with this article.
REFERENCES
- K. G. Asadov, S. K. Mamedov, “New Principles for Constructing a Measurement System Complex for Remote Sounding of a Seismological Situation,” Measurement Techniques, Vol. 48, No. 9, 2005, pp. 878-882. doi:10.1007/s11018-005-0238-2
- K. G. Asadov, “Synthesis of One Class of Information Measuring System According to the Principle of Dimensionality Reduction,” Measurement Techniques, Vol. 44, No. 3, 2001, pp. 240-245.doi:10.1023/A:1010905318642
- K. G. Asadov, “Synthesis of Optimal Subsystems for Processing Measurement Information Utilizing Parallel and Series-Parallel Transducers,” Measurement Techniques, Vol. 45, No. 2, 2002, pp. 137-140. doi:10.1023/A:1015531519826
- K. G. Asadov, “Synthesis of One Subclass of Information Measuring System According to the Principle of Dimensionality Reduction,” Measurement Techniques, Vol. 45, No. 4, 2002, pp. 359-362.doi:10.1023/A:1019625607123
- K. G. Asadov, “Optimization and Synthesis of Dynamic Remote Sensing Extremal Data Measuring Systems,” Measurement Techniques, Vol. 45, No. 7, 2002, pp. 761- 764.doi:10.1023/A:1020920111844
- K. G. Asadov, “Application of the Principle of Parametric Reduction of Dimensionality for Synthesizing one Subclass of Information Systems and Planning a Measurement Experiment,” Measurement Techniques, Vol. 46, No. 6, 2002, pp. 529-535.doi:10.1023/A:1025402324944

