Journal of Geographic Information System
Vol.09 No.03(2017), Article ID:76914,13 pages
10.4236/jgis.2017.93020
Automatic Correction of DEM Surface Errors
Ahmed F. Elaksher
Civil Engineering Department, Cal Poly University, Pomona, CA, USA

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 21, 2017; Accepted: June 12, 2017; Published: June 15, 2017
ABSTRACT
The automation of extracting planner surfaces is a main field of research in digital photogrammetry. These surfaces are essential to generate three dimensional GIS databases. Surfaces are usually determined from either DEMs or images. Each dataset provides a different type of information. Thus, the combination of the two datasets should enhance the surface reconstruction process. This paper presents a new technique for generating 3D surfaces by combining both correlation-based DEMs and aerial images. The process starts by discriminating DEM points that represent planner surfaces using local statistics of neighboring elevations and intensities and point elevations. A segmented orthophoto is then used to group these points into different regions. The elevations of the points in each region are fed into a least squares adjustment model to compute the best-fit planner surface parameters. Refinement of surface borders is then performed using a region growing algorithm. The RMSE for five test sites showed a spatial accuracy of 5 - 8 cm.
Keywords:
Photogrammetry, DEM, Orthophoto, Planner Surfaces

1. Introduction
Three dimensional surfaces support a great number of applications including; city modeling, generation of 3D Geographic Information Systems (GIS), and topographic analysis. Hence, there is an increasing demand for automatic generation of 3D surfaces. However, the end products of current digital photogrammetric stations are usually Digital Elevation Models (DEMs). These models are digital representation of the terrain elevations sampled at a fixed grid interval over the surface of the Earth. Thus, the output is usually named 2.5D. The interval between the grid points is an important aspect that affects the user of such model. Automation of object surface reconstruction from digital images is currently one of the most important research fields in Photogrammetry [1] . The reconstruction of precise surfaces from imagery datasets is a very hard problem not completely solved and problematic in case of incomplete, noisy and sparse data [2] . In the last years different solutions for 3D modeling have been developed.
Some researchers worked on extracting rood planes from LIDAR dataset. A multi-scale LIDAR point cloud uses decomposition algorithm to exclude ground points and later form planer surfaces through local fitting methodologies is implemented in [3] . In [4] the Gibbs energy model of building objects is first defined to fit the buildings’ points and then refined to get rid of outliers and to define the building outlines. In [5] , a principal component analysis is performed for the local neighborhood of individual points to detect points belonging to planar objects then segment these points based on an adaptive cylinder neighborhood definition. A point clustering algorithm for extracting homogeneous segments in laser data is presented in [6] . The goal of the data clustering is to subdivide the data into disjoint regions each with a homogeneous property that distinguishes it from its surrounding regions. The workflow in [7] involved four major steps: dividing the dataset into overlapping tiles, detecting building regions in each title, merging overlapping regions in adjacent tiles, and finally 3D surfaces are extracted. Most of these studies use LIDAR datasets that fail to provide texture or spectral information.
Other researchers employed both aerial images and LIDAR point cloud for the same purpose. For example, an algorithm to delineate roof patches from LIDAR point cloud and orthorectified photos is presented in [8] . Geometric primitives are used in [9] to model building roofs then built a cost function using constraints from aerial imageries and LIDAR data. Other studies using both LIDAR and aerial images include the work performed in [10] where points on roof patches are first detected from the LIDAR point could and building edges are extracted from optical images. A hybrid modeling system that fuses LIDAR data, aerial images, and terrestrial photos is presented in [11] . The model consists of three steps. In the first step, surface outlines from a high-resolution aerial image are interactively extracted, then mapped to the LIDAR data using a six parameter transformation model. Then the two data sets are combined for full model reconstruction. In the third step, poses are automatically recovered from ground view images, and textures are generated and mapped to the refined models. These studies combine LIDAR with imageries, which are more expensive than imagery datasets.
While laser scanners pose several challenges due to their size and cost [12] , optical imageries offer affordable and cost effective tool for creating high quality and reliable DEMs, [13] . Therefore, in this paper we rely on aerial photos as our merely source of data. Related studies include a stereo matching algorithm for object surface reconstruction, [14] . The algorithm is based on integrating several stereo matching techniques. The matching problem was addressed by the integration of both signal- and feature-based approaches. A new feature for surface matching, i.e. the plateau feature, was added in the matching process. The plateau feature was defined as a 1D region with near constant grayscale. Dynamic programming was then used to solve the matching problem. This research only adjusts the DEM in a line-by-line mode and doesn’t consider the inter-line relation between the different lines. Another study for semi-automatic 3D spatial polygon extraction from a pair of colored aerial images is presented in [15] . The algorithm consists of several consecutive stages; initial pointing by a human operator, extraction of a bounding polygon in the left image space, estimation of the average height, transformation to the right image space, extraction of a bounding polygon in the right image space. Finally, an iterative process which matches both polygons and extracts the spatial polygon is carried out. This method relies on a pair of images which might not represent the entire ground because of hidden parts. Another algorithm for planner surface reconstruction from DEMs is highlighted in [16] . The algorithm consists of three stages. In the first stage, a segmentation process is used in order to obtain planner surface primitives from DEMs. In a second step, a rule-based approach decides which segments can be explained by a set of predefined planner surface models. Finally, surfaces are delineated by closing any gaps that have been caused by the deletion of unexplainable regions. This method uses only DEMs and don’t consider image data in the rectification. Using DEMs solely depends on the source of the DEMs and their quality. Unlike the presented method that benefit from both the imagery and the DEM and could be applied to any DEM and could be extended to other optical data sources such as satellite images.
2. Methodology
The proposed method includes the following steps. An orthophoto is first generated. In the next step, points representing planner surfaces are discriminated from the DEM and the orthophoto using three criteria. These criteria include two local measurements for the likelihood of a point to be a planner surface point. Point elevations are also employed in the discrimination process. Image regions are then extracted from the orthophoto using the split and merge image segmentation technique. A least squares adjustment model, [17] , is then applied to find the best-fit planner surface for each region using the contributing points. Borders of each surface are then delineated.
2.1. Orthophoto Generation
The aerial images used in this research are fully triangulated, i.e. interior and exterior orientation elements have been defined, using a photogrammetric software. The images are conventional vertical photographs at the scale of 1:4000 scanned at 30 mm. In addition, the employed DEM is generated using the previous software. Hence, the ground space coordinates for each DEM point is known. For each DEM point, the collinearity equations, Equation (1), [18] , is used to calculate the corresponding image pixel. An interpolated gray value is computed using bilinear interpolation, and used to generate the orthophoto.
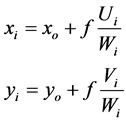 (1)
(1)
where: xo, yo ,and f are the camera interior parameters, xi, and yi are the corresponding pixel coordinates of point (i), 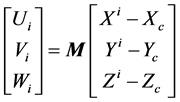 , where
, where 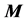 is the
is the
rotation matrix for the image, Xc, Yc, and Zc: are the exposure station coordinates for the image, and (Xi, Yi, and Zi) are the object space coordinates of point (i).
2.2. Discriminating Planner Surface Points
Planner surface points have several characteristics that could be used to discriminate them from other points. In this research three major characteristics are used. These characteristics include; a measure for the local plane fitting quality, the homogeneity of the gray levels for the surrounding points, the point height. Each characteristic could be used as a criterion in detecting planner surface points. However, the combination of the three criteria should lead to better detection of planner surface points.
2.2.1. Local Planner Criterion
This measure is calculated using a least squares adjustment model for a 3 × 3 local window. Input to the least squares model are the elevations for one DEM point and the surrounding eight points in the window. Equation (2) shows the employed least squares adjustment model. The output of the model are three parameters that represent the local plane that fit thought the local window. A local horizontal coordinate system is used in each window and centered at the center point of the window. To find a, b, and c, we use the principles of regres-
sion. We want to find a, b, and c, such that 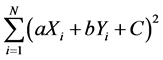 is minimum.
is minimum.
Therefore, we take the partial derivative with respect to a and set it equal to zero and we do the same for b and c. Hence, the unknown parameters are computed directly as shown in Equation (3). The parameters are then used to calculate an adjusted elevation for each point in the window. Figure 1 shows the proposed local window and the points elevations before and after the fitting process.
Figure 1. Elevations of the DEM Points in a Local Window before and after Fitting.
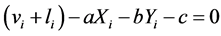 (2)
(2)
where:
li is the measured elevation for point (i),
vi is the residual of the measured elevation for point (i),
Xi and Yi are the X and Y ground coordinates for point (i),
a, b, and c are the local plane parameters, and
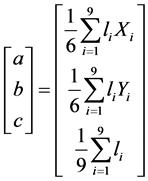 (3)
(3)
where:
a, b, and c are the three parameters that represent the planner surface,
li is the elevation of point (i) measured from the DEM, and
Xi, and Yi are the coordinates of the point (i) the local window.
The residual vector (V) is then computed and the value (VTV) for each window is then computed. This quantity is used as a measure of the fitting quality. Smaller quantities imply that the DEM point belongs to a planner surface. Large values mean that the DEM point doesn’t fit in a planner surface. Figure 2(a) shows the computed quantity for the 1st test area. Dark areas represent high quantities, while light areas represent low quantities.
2.2.2. Image Intensity Criterion
Pixels that represent planner surfaces should have similar intensities. The variation of the gray levels in the vicinity of such pixels should be small. For each pixel in the generated orthophoto a local window is generated. The size of the local window is 3 × 3. For each pixel, the standard deviation of the gray levels in the local window is computed. The standard deviation of the gray levels is used as

Figure 2. The 1st and 2nd Measured Criteria for 1st Test Site (higher values are darker). (a) The 1st criterion, (b) The 2nd criterion.
another criterion in the process of detecting planner surface points. Figure 2(b) shows the computed standard deviation of the gray levels in the orthophoto for the 1st test area.
2.2.3. Height Criterion
Planner surfaces usually describe man made features. These surfaces tend to be elevated above the bare terrain. However, DEMs measure the elevations of the ground surfaces. The combination of the DEM and the DSM should lead to information about elevated points. Hence, the extraction of the DSM is essential. Minimum filters are usually used in this task, [19] and [20] . The main objective of such filtering process is to detect and consequently remove points above the ground surface in order to recognize height DSM points in the data set. The minimum filter size should be large enough to include data points that are not part of the noise. However, iterative approaches could be used to avoid the effect of noise. In this research, the size of the minimum filter window is 3 × 3. The filtering is repeated iteratively until the DSM is extracted. Figure 3 shows two perspective views of the 1st test site. The first view represents the original DEM, while the second view represents the extracted DSM. In this test site, the maximum height in the DEM is 227 meters, while the maximum height in the DSM is 206 meters. The minimum elevation in both models is 195.6 meters. The results show that even when the bare ground is not flat, the filtering process is capable of extracting the DSM.
2.3. Extraction of Image Regions
There are several image segmentation techniques in the literature that could be used to extract image regions. These techniques show good results if the intensities of the image regions are approximately the same. In addition, high contrast between the region and surrounding objects should exist. The split and merge image segmentation technique [21] showed good results with such situation. In this research, the split and merge image segmentation technique is used.
The split and merge image segmentation is described as follows: first, splitting the image. The image is recursively divided into smaller regions until a homogeneity condition is satisfied. This is done using a quad-tree representation. Then adjacent regions are merged to form larger regions based upon the previous criterion. In the last step, small regions are either eliminated or merged with bigger regions. The criterion used in the split and merge image segmentation method is that the difference between the minimum and maximum intensities is less than a certain threshold. Holes are then automatically detected using a region growing algorithm [22] . Based on the average intensity of the holes, they are either eliminated or merged with the surrounding regions. Figure 4 shows the orthophoto image before and after the segmentation process for the 1st test site.
2.4. Extraction of Planner Surfaces
Each outcome of the previous processes could be used individually for the detection of the planner surface points. However, the combination of the previous
Figure 3. The DEM and the DSM for 1st test site (units in meters).
Figure 4. Original and Segmented Orthophoto for 1st Test Site.
criteria in the discrimination process should lead to higher quality description of planner surfaces. The literature describes a number of techniques for the combination of such information. An object-based classification rather than pixel-based classification is used in [23] . A knowledge-based classification considering elevation, spectral, texture, and shape information is used in [24] .
In this research a rule based algorithm is used to detect planner surface points. The algorithm starts by normalizing the output of the three computed criteria. For the first and second criteria the differences between the maximum and minimum values is computed. Then, for each criterion a normalized value is computed using Equation (4). The larger the value in each normalized output, the more likely the point will belong to a planner surface. In the next step, the differences between the DEM and the DSM are computed. Equation (3) is then used to normalize the differences between the two models.
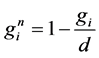 (4)
(4)
where:
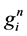 is the normalized value for point (i),
is the normalized value for point (i),
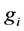 is the original value for point (i), and
is the original value for point (i), and
d is the difference between the maximum and minimum values of the output.
The three normalized values and the segmented image are used to detect planner surface points as follows. First, the average of the three normalized outputs are computed for each point. If the average is greater than 0.75 and the value of each normalized value for that point is greater than 0.9 the point is detected as a planner surface point. Noise and small regions are removed using a region growing process. Neighboring planner surface points are connecting and if the size of the region is smaller than a given threshold the region is removed. In this research a threshold of 10 - 25 points is used. The result for the 1st test area is shown in Figure 5.
For each region in the region-based orthophoto, its correspond planner surface points are counted. If the number of these points is more than 90%, this region is believed to be a planner surface. Other regions are eliminated. Elevations of points belonging to a planner surface region are employed in a least squares adjustment. In the adjustment model, the elevations of all the region points are used as observations. Unknowns are the surface parameters. Since only planner surfaces are assumed, only three parameters for each region are used. Equation (5) shows the least squares adjustment model employed to compute the plane parameters. These parameters are then used to compute the adjusted elevations of each point in the DEM that belongs to a planner surface.
 (5)
(5)
Figure 5. Points Detected as Planner Surface Points.
where:
a, b, and c are the three parameters that represent the planner surface,
li is the elevation of point (i),
Xi, and Yi are the coordinates of point (i), and
n is the number of points in the planner surface region.
In order to delineate border points for each region, a refining step is then implemented. For each region, the neighboring points for each border point are located. Each neighboring point that doesn’t belong to the region is tested if it could be appended to the region. The test is based on the difference between the point elevation and the expected elevation using the three parameters of the planner surface of the region. If the point is appended to the region the parameters are recomputed and updated. In addition, the elevations of the region points, including the appended points, are recomputed. This process is repeated iteratively until no more neighboring points are appended. Figure 6 shows the final extracted planner surfaces for the 1st test site.
3. Experimental Results and Analysis
To test and verify the proposed algorithm, a C++ program was developed using Microsoft Visual Studio 6.0. The employed DEMs are generated with a one meter interval. Five test sites are used to test the proposed algorithm. Figure 7 shows the extracted planner surfaces for the reaming four test sites. Results are evaluated both visually and numerically. The visual evaluation shows that plan-
Figure 6. Extracted Planner Surfaces for 1st test site.




Figure 7. Extracted Planner Surfaces for 4 Test Sites.
ner surfaces in all test sites are detected. Moreover, no false surfaces were extracted. However, for some surfaces the borders are not well delineated. The process is affected by outlier or missing points in the extracted regions. This is due to the sensitivity of the segmentation process. In addition, noise in the vicinity of elevation discontinuities also affects the results.
Numerical evaluation is based on computing the Root Mean Square Errors (RMSE) for differences in elevations. Numerical evaluation is performed only for points contributing to planner surfaces. Extracted surfaces are divided to two groups, horizontal and non-horizontal. For horizontal surfaces, reference elevations are measured manually for all corner points and a mean value is computed. This value is used to evaluate the elevations of the planner surface corners. For
Table 1. RMSE for the refining process.
non-horizontal surfaces, the reference elevations are measured manually for three corner points and used to compute the true parameters of the planner surfaces. These parameters are then used to compute several reference elevations using the exact horizontal coordinates (X and Y). The RMSE of the differences between the reference elevations and the computed elevations using the presented technique are computed and presented in Table 1. Results show that the average RMSE for horizontal surfaces is about 5.3 cm. The average RMSE for inclined surfaces is about 8 cm. In addition, for each test site a reference DEM is collected manually. The average RMSE for the employed DEMs is about 10 cm. This algorithm works perfectly for any type of building; however, the limitation is cases where there are parts of the buildings covered by trees. It is also sensitive to the slopes of the roof patches, i.e. cases where different roof segments with different orientations might not be differentiated.
4. Conclusions and Recommendations
This paper shows the potential of generating 3D planner surfaces by integrating elevation data, provided by correlation-based DEMs, and image intensities. DEM points contributing to planner surfaces are discriminated from other DEM points using different features. Points contributing to each planner surface are then used to fit a plane through this surface using a least squares adjustment model. Input to the model are the 3D coordinates of all DEM points that contribute to the surface. The model is then solved to find the best plane that fit these points. Results show that the proposed process is able of detecting all tested planner surfaces with no false surfaces. The spatial accuracy shows that the RMSE for the elevations of a number of manually selected planner surface points is about 5 cm to 8 cm. The RMSE depends on the inclination of the surface. Future research will focus on testing the proposed algorithm on laser-based DEMs. In addition, other discrimination features to classify planner surface points could be tested. Other techniques for combining the proposed features such as belief networks, expert systems, or fuzzy logic systems could be used. Our algorithm should work with any configuration of roofs; however, if any part of the building is covered by trees it could fail.
Cite this paper
Elaksher, A.F. (2017) Automatic Correction of DEM Sur- face Errors. Journal of Geographic Information System, 9, 326-338. https://doi.org/10.4236/jgis.2017.93020
References
- 1. Rottensteiner, F. (1998) Object Reconstruction in a Bundle Block Environment. International Archives of Photogrammetry and Remote Sensing, Columbus, Ohio, USA, Vol. 32 (3/1), 6-10 July 1998, 177-183.
- 2. Remondino, F. (2003) From Point Cloud to Surface: The Modeling and Visualization Problem. Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Tarasp-Vulpera, Switzerland, Vol. 34 (5/W10), 24-28 February 2003 (on CD-ROM).
- 3. Mongus, D., Lukac, N. and Zalik, B. (2014) Ground and Building Extraction from LiDAR Data Based on Differential Morphological Profiles and Locally Fitted Surfaces. ISPRS Journal of Photogrammetry and Remote Sensing, 93, 145-156.
- 4. Yang, B.S., Xu, W.X. and Yao, W. (2014) Extracting Buildings from Airborne Laser Scanning Point Clouds Using a Marked Point Process. GIScience & Remote Sensing, 51, 555-574.
https://doi.org/10.1080/15481603.2014.950117 - 5. Lari, Z. and Habib, A. (2014) An Adaptive Approach for the Segmentation and Extraction of Planar and Linear/Cylindrical Features from Laser Scanning Data. ISPRS Journal of Photogrammetry and Remote Sensing, 93, 192-212.
- 6. Filin, S. (2002) Surface Clustering from Airborne Laser Scanning Data. Proceedings of the International Archives of Photogrammetry and Remote Sensing, Graz, Austria, Vol. 32(A), 9-13 September 2002, 119-124.
- 7. Jochem, A., Hofle, B., Wichmann, V., Rutzinger, M. and Zipf, A. (2012) Area-Wide Roof Plane Segmentation in Airborne LiDAR Point Clouds. Computers, Environment and Urban Systems, 36, 54-64.
- 8. Gilani, S.A.N., Awrangjeb, M. and Lu, G.J. (2016) An Automatic Building Extraction and Regularisation Technique Using LiDAR Point Cloud Data and Orthoimage. Remote Sensing, 8, 258.
https://doi.org/10.3390/rs8030258 - 9. Zhang, W.M., Wang, H.T., Chen, Y.M., Yan, K. and Chen, M. (2014) 3D Building Roof Modeling by Optimizing Primitive’s Parameters Using Constraints from LiDAR Data and Aerial Imagery. Remote Sensing, 6, 8107-8133.
https://doi.org/10.3390/rs6098107 - 10. Li, Y., Wu, H.Y., An, R., Xu, H.W., He, Q.S. and Xu, J. (2013) An Improved Building Boundary Extraction Algorithm Based on Fusion of Optical Imagery and LIDAR Data. Optik-International Journal for Light and Electron Optics, 124, 5357-5362.
- 11. Hu, J., You, S. and Neumann, U. (2006) Integrating LIDAR, Aerial Image and Ground Images for Complete Urban Building Modeling. 3rd International Symposium on 3D Data Processing, Visualization and Transmission, Chapel Hill, 14-16 June 2006.
https://doi.org/10.1109/3dpvt.2006.82 - 12. Colomina, I. and Molina, P. (2014) Unmanned Aerial Systems for Photogrammetry and Remote Sensing: A Review. ISPRS Journal of Photogrammetry and Remote Sensing, 92, 79-97.
- 13. Ruiz, J.J., Diaz-Mas, L., Perez, F. and Viguria, A. (2013) Evaluating the Accuracy of DEM Generation Algorithms from UAV Imagery. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 40, 333-337.
https://doi.org/10.5194/isprsarchives-XL-1-W2-333-2013 - 14. Apaphant, P. and Bethel, J. (2000) Integration of Object and Feature Matching for Object Surface Extraction. The International Archives of Photogrammetry and Remote Sensing, Amsterdam, Vol. 31, 16-22 July 2000, 267-273.
- 15. Avrahami, Y., Raizman, Y. and Doytsher, Y. (2005) Extraction of 3D Spatial Polygons Based on the Overlapping Criterion for Roof Extraction from Aerial Images. Joint Workshop of ISPRS and the German Association for Pattern Recognition: Object Extraction for 3D City Models, Road Databases and Traffic Monitoring-Concepts, Algorithms, and Evaluation, Vienna, 29-30 August 2005.
- 16. Brenner, C. and Haala, N. (2001) Automated Reconstruction of 3D City Models. In Abdelguerfi, M., Ed., 3D Synthetic Environment Reconstruction, Kluwer Academic Publishers, 75-101.
https://doi.org/10.1007/978-1-4419-8756-3_4 - 17. Mikhail, E.M. (1974) Observation and Least Squares. University Press, New York.
- 18. Mikhail, E., Bethel, J. and McGlone, J. (2001) Introduction to Modern Photogrammetry. John Wiley & Sons Inc., New York, 96-97.
- 19. Masaharu, H. and Ohtsubo, K. (2002) A Filtering Method of Airborne Laser Scanner Data for Complex Terrain. The International Archives of Photogrammetry and Remote Sensing, Graz, Vol. 32, 9-13 September 2002, 165-169.
- 20. Wack, R. and Wimmer, A. (2002) Digital Terrain Models from Airborne Laser Scanner Data—A Grid Based Approach. The International Archives of Photogrammetry and Remote Sensing, Graz, Vol. 32, 9-13 September 2002, 293-296.
- 21. Horowitz, S.L. and Pavlidis, T. (1974) Picture Segmentation by a Direct Split and Merge Procedure. 2nd International Joint Conference on Pattern Recognition, August 1974, 424-433.
- 22. Rosenfeld, A. and Kak, A.C. (1982) Digital Picture Processing. 2nd Edition, Academic Press, New York.
- 23. Chen, L.-C., Teo, T.-A., Shao, Y.-C., Lai, Y.-C. and Rau, J.-Y. (2004) Fusion of LIDAR Data and Optical Imagery for Building Modeling. The International Archives of Photogrammetry and Remote Sensing, Istanbul, Vol. 35, 12-23 July 2004, 732-737.
- 24. Hofmann, A.D., Mass, H. and Streilein, A. (2002) Knowledge Based Building Detection Based on Laser Scanner Data and Topographic Map Information. The International Archives of Photogrammetry and Remote Sensing, Graz, Vol. 32, 9-13 September 2002, 166-174.









