Journal of Geographic Information System
Vol.09 No.02(2017), Article ID:75965,33 pages
10.4236/jgis.2017.92011
Morphometric Assessment of Wadi Wala Watershed, Southern Jordan Using ASTER (DEM) and GIS
Yahya Farhan
Department of Geography, University of Jordan, Amman, Jordan

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 27, 2017; Accepted: April 27, 2017; Published: April 30, 2017
ABSTRACT
Morphometric analysis is of vital concern to understand hydromophological processes in a given watershed, and thus, it is a priority for assessing water resources in drainage basins. A morphometric analysis was conducted to identify the drainage properties of Wadi Wala and the 23 fourth-order sub- basins. ASTER DEM data was employed to compile slope, elevation, and aspect maps. Arc GIS software was used to measure and calculate basic, derived and shape morphometric parameters. W. Wala is found to be a sixth-order drainage basin, and the drainage pattern is trellis to sub-trellis in the central and lower part of the catchment, whereas it is dendritic to sub-dendritic pattern in the southern and northern parts. The slopes of the catchment vary from 0˚ - 5˚ to >35˚ in slope categories. Tectonic uplifting and tilting, lithology, structure and rejuvenation are the major factors controlling morphological variation over the watershed. The recognized fault systems are chiefly controlling the drainage pattern, and the elongated shape of the sub-basins is attributed to dense lineaments in the central and eastern parts of the watershed. The Rb values for the entire catchment and the sub-catchments range from 2 to 7, with a mean of 4.55, which indicates the distortion of drainage pattern by geological structure. Hypsometric integral values are high for the W. Wala watershed and the sub-basins, where it ranges from 70% to 89%. High HI values indicate that drainage basins are at the youth-age stage of geomorphic development, and they are affected by tectonic uplifting, tilting, and the dominance of hillslope process. Variation in HI values is apparent between sub-basins located at the western part, or, the rejuvenated belt where HI values range from 85% to 89%. Whereas the HI values of the sub-basins located at the eastern part of the watershed, vary from 70% to 84%. Regression analysis reveals that R2 values, which represent the degree of control of driving parameters on HI are reasonably high for the height of local base level (m) and the mean height of sub-basins (m). Both parameters contribute 0.42 and 0.39 respectively (where the F-value is significant at 0.1% and 0.5% levels). Such results imply that the height of local base level (m), and the mean height (m) are the only morphometric driving parameters which have significant control on HI values in the W. Wala watershed. High annual soil loss and sediment load estimated recently, denote that the catchment is highly susceptible to surface erosion at present. Hence, the present study, and the resultant information would help to plan for efficient soil and water conservation measures to reduce soil erosion rates, conserve water, and to control sediment into W. Wala dam.
Keywords:
GIS, ASTER DEM, Morphometry, Rejuvenation, Lineaments, Topographic Dissection

1. Introduction
A drainage basin is recognized as a fundamental hydro-geomorphic unit for watershed management [1] . Therefore geomorphometric indices and parameters have been widely employed to investigate the sustainable development of natural resources. Morphometric characteristics of a watershed are significant for assessing surface water resources and groundwater potential [2] [3] . Geomor- phometric properties are also essential for proper utilization of land and water resources of a catchment for optimum production with minimal environmental hazards (i.e. severe soil erosion, high sediment yield rates, landslide activity and flooding)to protect the people who live across the catchment, or in occupied areas near the outlet of a watershed [3] [4] [5] [6] . Morphometry refers to the measurement and evaluation of the configuration of the earth’s surface, including the shape and dimensions of its landforms, and different aspects of drainage basins [7] . Morphometric analysis is performed through the measurement and calculation of basic parameters, derived parameters, and shape parameters of drainage basins using DEM’s, GIS tool, and mathematical equations developed for this purpose [8] [9] [10] [11] . The measured bifurcation ratio (Rb) for example refers to the degree in which geological structure controls the drainage network, whereas, a high value of mean bifurcation ration (Rbm) of a drainage system indicates the runoff and other external agents that contribute to the formation of drainage networks [12] [13] . Assessment of geo-environmental hazards especially flash floods was carried out for arid watersheds which occasionally threaten small and large areas of human settlement [14] - [21] . Watershed prioritization for soil and water conservation, and site selection for water harvesting, were conducted recently based on morphometric analysis, sediment yield estimation, land use/cover, and soil erosion modeling using GIS and remote sensing [4] [6] [22] - [27] . Other applications of morphometric analysis have been conducted worldwide such as: studying the imprints of Quaternary active tectonics over structures and drainage basins [28] [29] [30] [31] [32] , tectonic control on geomorphic processes in shaping drainage networks [33] , and landslides coupled with their triggering mechanisms [34] . Geology (lithology and structure), morphology (relief and slope), and climate (precipitation and evaporation) constitute a major complex of physical factors controlling the drainage pattern, density, and geometry of the fluvial system [35] . The relative influence of each factor on fluvial activity varies from one region to another, and subsequently there are noticeable differences exhibited in morphometric properties between drainage basins. Furthermore, the hydrological descriptors of drainage basins (including arid catchments) are positively correlated with morphometric parameters of a watershed, such as: slope, shape, size, drainage density, elevation, basin length, maximum stream length, and total length of stream segments etc. [36] . The hydrological behavior of a drainage basin is largely determined by its geomorphic, geologic, climatic, and morphometric characteristics as defined by linear, areal and relief aspects of the basins [37] [38] . Quantitative morphometric analysis of drainage networks and other properties is traditionally tackled by geomorphologists, hydrologists, and civil engineers. In this context, Strahler [39] argued that morphometric analysis is considered a simple study approach, thus, enabling assessment of basin morphology and processes, and morphometric comparison of different basins developed in different environments. Such approaches enhance our understanding of the geomorphic evolution of drainage basins. It was also concluded in the recent past that any significant changes affecting any environmental component of the watershed, will influence other components especially those located downstream, denoting that any natural or anthropogenic geomorphic and hydrologic changes taking place, will instantly affect certain areas, and may spread to other parts of the watershed [40] . The development of powerful and cost-effective GIS and remote sensing techniques enables us to measure, calculate, and process with high accuracy basic, derived, and shape morphometric parameters of drainage basins. Further, the availability of free access digital elevation data (i.e., STRM and ASTER DEMs) of high resolution, have enhanced rapid quantification of drainage networks, morphometric thematic mapping, and thus, have expanded the applications of morphometric analysis to other fields of research. The main objectives of the present study are:
1) Analyze morphometric properties of W. Wala watershed, and the related 23 fourth-order sub-watersheds, using GIS and ASTER DEM data.
2) Explore the physical behavior and interrelations between morphometric parameters in arid watersheds and sub-watersheds using regression analysis.
3) Statistical evaluation was carried out (RL), and the number of streams and stream lengths in relation to stream order.
Considering W. Wala as an agricultural watershed, and a promising catchment for future water resources development, morphometric analysis and the resultant information are significant for proper planning of soil and water conservation measures, to minimize soil erosion rates and sediment load, exploration of groundwater potential, and surface water management. Moreover, the present results can also help other investigations that may be carried out in the watershed study.
2. Study Area
The W. Wala catchment occupies the upper part of W. Mujib-Wala watershed, covering a triangular shaped catchment of 2063.6 km2. It lies between 35˚65'E to 36˚30'E Longitudes, and 31˚55'N to 31˚90'N latitudes (Figure 1). Terrain elevation ranges from-327 m (b.s.l) at the point where W. Wala merges with W. Mujib (3 km before the wadi system discharge into the Dead Sea) to 1007 m (a.s.l) northwest of the watershed (Figure 2(a) and Figure 2(b)). Flat/undulating terrain (0˚ - 5˚) and (5˚ - 10˚) dominates the eastern part of the watershed, whereas, steep slopes (>35˚) and dissected terrain characterize the western parts (Figure 3).
The climate is classified as dry Mediterranean, with relatively cold winters and hot summers, while the canyons downstream close to the Dead Sea are arid. Mean annual rainfall ranges from 346 mm at Madaba (several kilometers to the northwest of the watershed) to 282 mm at Dhiban, and 266 mm at W. Wala weather station. The average annual rainfall for the entire watershed ranges between 100 and 200 mm. Rainfall is concentrated in winter (October to March). Large seasonal variations in temperature are evident, where daily temperatures range from a maximum of >40˚C in August to a minimum of −5˚C in January. The mean annual potential evaporation at the outlet close to the Dead Sea is 2200 mm, with a mean that increases from 1600 mm in the western highlands to 2000 mm in the eastern part of the watershed. Cretaceous carbonate rocks outcrop in most of W.Wala catchment. The oldest rocks exposed in the study area are the Massive limestone unit of Turonian age. The lower part is composed of marl, marly limestone, sand, and chert nodules, while the upper part is composed
Figure 1. Location of Wadi Wala, the study area.


Figure 2. (a) DEM of W. Wala watershed. (b) Contour map of W. Wala catchment.
of limestone, dolomitic limestone and fossiloferous limestone. The average thickness of this lithological unit is 67 m. The chalky unit of W. Umm Ghudran (Coniacian-Santonian age) overlies the Massive limestone unit. It consists of Mujib-Dhiban Chalk, brecciated dolomitic limestone. Amman Silicified Limestone, Al Hisa phosphorite formation, and the Muwaqqar Chalk-marl formation, all of Maestrichtian-Campanian-Santonian age. It consists of thin bedded silicified limestone and chert layers. The phosphorite formation is composed of
Figure 3. Slope categories.
thin-bedded limestone, silicified phosphorite and layers of minable phosphate. This formation is 90 m thick. The chalk-marl formation reposes on top of the phosphorite formation, and ranges in thickness from 20 to 450 m. It consists of marl and chalk with chalk limestone. The chert-limestone formation overlies the chalk-marl member. Massive chalk limestone, alternating thin bedded limestone and chert layers, and range in age from early Paleocene to middle Eocene [41] . Basaltic flows of the Pleistocene age are exposed in the upper reaches of W. Wala. Additionally, superficial deposits of Fluviatile and Lacustrine Gravels of the Pleistocene age covers parts of the deep tributaries of W. Wala. The most important aquifers in W. Wala are those restricted to Amman-W. As Sir limestone (Upper Cretaceous), with mediating W. Umm Ghudran and overlying the Muwaqqar Chalk-Marl formations, forming aquicludes. This aquifer is termed A7-B1 [42] [43] . The Ministry of Water and Irrigation constructed the W. Wala reservoir (2003) with a capacity of ≈10 MCM. The future plan is to raise the height of the reservoir to store 26 MCM. The reservoir is intended for groundwater recharge, and to provide water to springs and pumping wells in the lower courses of the wadi. Progressive rejuvenation, down-cutting and river incision of W. Wala were the result of continuous lowering of the Dead Sea base level. Tectonic uplifting of the eastern shoulder of the Dead Sea Rift during Late Tertiary and Quaternary tectonics have resulted in irregular slope segments (15˚ - 35˚) separated by rocky benches. The wadi profile display well?defined discontinuities which probably represent some form of rejuvenated points. In this regard, four or five rejuvenation stages can be recognized [44] [45] . Rejuvenation processes have resulted in a “poly-cyclic” drainage basin as concluded earlier by Chorely [46] . It is certain that geomorphic development, rejuvenation, and intense incision are responsible for the presence of sharp convex upward hypsometric curve and a high HI value (88.14%). The shape of the HC and high HI value denotes that W. Wala watershed and the sub-watersheds are at the youth-age stage of geomorphic evolution. Thus, they are of high susceptibility to soil erosion, deep incision, landslides activity and flooding [47] . Open rangelands constitute 47% of the catchment area. Rainfed cultivation of cereals (wheat and barley) is practiced in 38% of the total area of the watershed, whereas, 7% of the catchment is urban [43] .
3. Materials and Methods
Topographic maps with a scale of 1:50,000 (20 m contour interval) were purchased from the Royal Jordanian National Geographic Centre (RJNGC), Amman, published 1992). Topographic information was digitized and geo-refe- renced with UTM Projection, WGS 1984, Zone 36˚N using Arc GIS software (10.1). Using the Spatial analyst Module an ASTER DEM (v.2) (30 m resolution) was generated. Then the boundaries and drainage networks of the entire W. Wala and the 23 fourth-order sub-watersheds were demarcated and digitized using Arc GIS (v.10.1) tools (Figure 4). Three groups of morphometric parameters: basic, derived, and shape parameters were measured and calculated quantitatively using Arc GIS packages, the mathematical equations developed by Strahler [39] [48] [49] , and ASTER DEM. Basic parameters are basin area (A), perimeter (P), basing length (Lb), stream order (u), stream length (Lu), mean stream length (Lsm), maximum and minimum heights (H, h), and slope (Sb). Derived parameters are bifurcation ratio (Rb), stream length ratio (RL), RHO coefficient (ρ), stream frequency (Fs), drainage density (Dd), drainage texture (Dt), basin relief (Bh), relief ratio (Rr), ruggedness number (Rn) and hypometric integral
Figure 4. The 23 sub-watersheds of W. Wala catchment.
(HI). Shape parameters are elongation ratio (Re), circularity ratio (Rc), and form factor (Rf). The stream ordering of the entire W. Wala watershed and the 23 sub- watersheds was implemented according to Strahler [39] , and the W. Wala catchment was found to be of sixth order. Derivatives of DEM were also slope categories, aspect and elevation maps using the spatial analyst tool available in Arc GIS. The methods adopted for calculation of morphometric parameters are illustrated in Table 1, and results of computation are illustrated in Table 2, and Table S1. Regression analysis is employed to assess the interrelationship between the area of sub-watersheds and other morphometric parameters, where the basin area is considered an independent variable, and other morphometric parameters are dependent variables. In addition, the scale dependency of HI values for 10 sub-wa- tersheds was conducted to evaluate the effect of different driving parameters (i.e., stream order, basin area (km2), height of local base level (m), elongation ratio, form factor, and mean height (m) on hypsometric integral. The value of R2 represents and indicator of the degree of control of these parameters on HIs.
4. Morphometric Assessment of W. Wala Watershed
Quantitative analysis was performed for W. Wala catchment and the 23 fourth- order sub-watersheds in order to evaluate the morphometric properties of the drainage networks. Twenty-one morphometric parameters were considered to characterize the watershed and to improve our understanding of drainage basin development with reference to intrinsic controlling factors such as lithology, structure and tectonics geomorphic processes and rejuvenation stages. The results of morphometric analysis for the entire catchment and the 23 sub-basins are illustrated in Table 2, and Table S1. The drainage pattern is trellis to sub-trellis in the central and lower parts of the watershed, whereas it is dendritic to a sub-dendritic pattern in the southern and northern parts. The W. Wala catchment is classified as a sixth-order basin (Figure 5). Referring to the ratio between basin area (A) and perimeter (P) (5.127:1), the borderline of W. Wala is a relatively irregular water divide.
4.1. Basic Morphometric Parameters
The basic morphometric parameters calculated for W. Wala and the 23 sub-ba- sin consists of basin area (A), basin perimeter (P), basin length (Lb), stream order (u), stream length (Lu) and mean stream length (Rbm), and maximum and minimum heights of basin (H and h).
4.1.1. Basin Area (A), Basin Length (Lb), and Basin Perimeter (P)
Drainage area (A) is a fundamental morphometric parameter for hydrological data processes, analysis and interpretation. Larger basins and sub-basins with high relative relief are generally characterized by greater discharge, and directly influenced the peaks and runoff magnitudes. Thus, the basin area is an essential component in hydrological processes [21] . In this context, Chorley et al. [50] concluded that the maximum discharge of flood per unit area, is inversely related to the size of the drainage basin. The total drainage area for W. Wala is
Table 1. Morphmetric parameters and their mathematical formula.
Table 2. Morphometric characteristics of W. Wala catchment.
2063.6 km2, and for the 23 sub-basins, it ranges from 18 km2 to 184.99 km2. The basin length corresponds to the maximum length of the watershed and sub-wa- tersheds measured parallel to the main drainage line. The length of W. Wala is 88.8 km, while the lengths of the sub-basins vary from 5.423 to 38.186 km. The perimeter of W. Wala is 403.9 km, and the perimeters of the sub-basins range from 17.59 to 153. 578 km (Table S1). Sub-watershed 23 represents the shortest, but with longest perimeter, while sub-watershed 13 is the longest, but with the
Figure 5. Stream order of W. Wala watershed.
highest perimeter. In terms of area, sub-watershed 12 is the largest, and sub- watershed 10 is the smallest. However, the greater area sub-basins and the longest, are generally located close to the northwestern, south-eastern, and the eastern borders of the main catchment. Whereas the shortest in length and smallest in area are located in the rejuvenated belt due to the dominance of steep slopes and topographic dissection.
4.1.2. Stream Order (u) and Stream Number(Nu)
Stream ordering or, categorization of streams based on the number and type of tributary junction has been treated as a useful indicator of stream size, discharge and drainage area [39] . The total number of streams (Nu) is 2476, and the first order streams account for 78.2% of the total number of streams in W. Wala catchment. The details of stream characteristics support Horton’s [51] first law or, the “law of stream numbers”, which states that the number of streams of different orders in a given drainage basin tends to closely approximate an inverse geometric ratio. Such an inverse geometric relationship is illustrated graphically in the form of a straight line when log values (Nu) are plotted on an ordinary graph (Figure 6(a)). W. Wala watershed is composed of 23 sub-basins which are designated as fourth-order basins, and 5 sub-basins of fifth-order only.
4.1.3. Stream Length (Lu)
Stream length is measured from the origin of a stream to the drainage divide. Lu is a dimensional parameter employed to understand the characteristics of the elements of the drainage network and its contributing basin surfaces [39] . It expresses the hydrological properties of the underlying bedrocks. A small number of longer stream lengths are often developed where the bedrocks are permeable,

Figure 6. (a) Horton’s first law of stream number, and (b) Horton’s second law of stream length using W. Wala data.
while a larger number of small stream lengths are formed where the rock material is less permeable [20] . The stream length characteristics of the W. Wala catchment and the 23 sub-basins fulfills Horton’s [51] “law of stream length”, which states that “the average length of streams of each of the different orders in a drainage basin tends closely to approximate a direct geometric ratio”. This geometric linear relationship in displayed graphically when log values of these parameters are plotted on an ordinary graph (Figure 6(b)). Generally, most drainage basins and sub-basins show an almost linear relationship with a small deviation from a straight line as reported by [52] . The total stream length (Lu) of W. Wala is 2839.2 km, and the first-order streams represent 49.9% of the total stream length.
4.1.4. Mean Stream Length (Lsm)
Lsm is defined by dividing the total stream length of order (u) and number of stream segments of the same order (u). The mean stream length for W. Wala varies from 0.732 for the first order streams to 67.8 for the sixth-order stream (Table S1), and the Lsm value for any given order is greater than that of the lower order and less than that of its next higher order. For the 23 sub-watersheds, the Lsm values range from 0.5999 for the first-order streams, to 24.734 for the fourth-order stream.
4.1.5. Maximum and Minimum Heights (H, h)
The maximum and minimum elevation resemble the highest and lowest point of the watershed and sub-watersheds. The highest elevations of W. Wala correspond to the northwestern and southwestern zones of the basin, and the lowest elevation predominates in the central part of the catchment. The H and h values for the entire watershed are 1007 m and 327 m respectively. Likewise, the (H) values for the sub-watersheds vary from 800 m to 1007 m, and the (h) values range from 513 m to 821 m. Accordingly, the maximum and minimum height values vary for the sub-watersheds, but they are substantially high.
4.1.6. Slope (Sb)
Slope of drainage basins as a morphometric factor is considered to be of hydrological significance [8] . Steep slopes occasionally have high surface runoff values and low infiltration rates, which in turn accelerate soil erosion. Thus, sediment load production tends to be high especially in over-grazed barren slopes [53] . According to Mesa [8] , the catchment slope was computed applying the following formula.
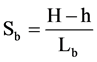
where H and h are the maximum and minimum basin heights respectively; and Lb is the horizontal length of the catchment. The slopes recorded vary from 0˚ to cliffs >50˚ of slope. The slopes extracted from ASTER DEM are categorized into 0˚ - 5˚, 5˚ - 10˚, 10˚ - 15˚, 15˚ - 20˚, 20˚ - 30˚ and >30˚ (Figure 3). Slope categories of 0˚ - 5˚ to 10˚ - 15˚ characterize the central part of the watershed, while slopes> 50 dominated the lower part where the canyon-shaped wadis established downstream. The general slope of W. Wala is 14˚ approximately, although steep slopes and rugged dissected terrain characterize the western part or the rejuvenated belt of the watershed. The slope values for the sub-watersheds range from 5.5˚ to 41.3˚. Slopes of sub-basins generally increased from east to west.
4.2. Derived Morphometric Parameters
4.2.1. Bifurcation Ratio (Rb)
The bifurcation ratio (Rb) is defined as the ratio of the number of streams of a given order (Nu) to the number of streams in the next higher order (Nu + 1). The Rb parameter is elaborated by Horton [51] as a morphological index of relief and dissection. The value of Rb for flat or rolling catchments is about 2, and for highly dissected watersheds, the value is up to 3 or 4. Rb parameter shows the geometric similarity of the drainage basin and endorses the divarication of the drainage network [39] . Values of Rb for W. Wala and the 23 sub-watersheds range from 2 to 7, with a mean of 4.55. Such figures demonstrate that the watersheds are crucially affected by structural disturbances, where the drainage branching is heavily controlled by geological structure represented by Wadi Zerqa Ma’in fault, W. Wala fault, Az-Za’faran fault, and Wadi Al Falij small faults [43] and the resultant lineaments.
4.2.2. Stream Length Ratio (RL)
The watershed and watershed ratios refer to the ratio between the mean length of streams of a given order (Lu) to the mean length of streams in the next lower order (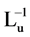 ). Stream length ratio is an important parameter in relation to drainage composition and geomorphic evolution of drainage basins [39] . RL values vary between successive streams order as a result of variation in relief and slope conditions. RL also has a considerable relationship with surface flow discharge and erosional stage of the watershed (Sreedevi et al. 2004). Relative variation exists in RL values between streams of different order pertaining to W. Wala (0.41 to 0.96). Such variation is attributed to geomorphic changes in relief and slope, the stage of geomorphic development and rejuvenation status along W. Wala watersheds. The value of RL for W. Wala is 0.56, whereas RL values for the 23 sub-basins range from 0.034 for the first-order streams to 0.858 for the fourth- order streams.
). Stream length ratio is an important parameter in relation to drainage composition and geomorphic evolution of drainage basins [39] . RL values vary between successive streams order as a result of variation in relief and slope conditions. RL also has a considerable relationship with surface flow discharge and erosional stage of the watershed (Sreedevi et al. 2004). Relative variation exists in RL values between streams of different order pertaining to W. Wala (0.41 to 0.96). Such variation is attributed to geomorphic changes in relief and slope, the stage of geomorphic development and rejuvenation status along W. Wala watersheds. The value of RL for W. Wala is 0.56, whereas RL values for the 23 sub-basins range from 0.034 for the first-order streams to 0.858 for the fourth- order streams.
4.2.3. RHO Coefficient (ρ)
RHO coefficient is defined as the ratio between the stream length ratio (RL) and the bifurcation ratio (Rb) [51] . It is affected by geologic, geomorphic, climatic, biologic, and anthropogenic factors [8] . RHO is a significant variable that determines the relationship between Dd and the geomorphic evolution of a drainage basin. Therefore, it permits the assessment of the storage capacity of the drainage network [51] . High RHO value of a drainage network is indicative of high hydric storage during flooding, thus, the erosion effect is decreased during the raised discharge [8] . The RHO value for the entire W. Wala 1.22, and for the 23 sub-basin varies from 0.092 to 0.466.
4.2.4. Stream Frequency (Fs)
Stream frequency is defined as the ratio of the total number of streams (Nu) of all orders in a catchment and the basin area [51] . Fs is influenced by the underlying rock materials, thus, it is an indication of drainage texture of basins and sub-basins. The Fs values are positively correlated with Dd values of a watershed. Thus, any increase in stream population is associated with that of drainage density [3] . Low Fs values denotes that a relatively low infiltration rate of surface water is achieved; thus, the groundwater potential is relatively low [54] . Melton [55] stated that low value of stream frequency (1.0 to 3.5) indicates that the stream is controlled by fractures, and high stream frequency (4 to 10) denotes low impermeability and more surface runoff. The value of stream frequency for W. Wala watershed is 1.20 km−2, and for the 23 sub-basins, it ranges from 1.064 km−2 to 1.771 km−2. Such values imply that the W. Wala catchment is relatively of high runoff.
4.2.5. Drainage Density (Dd)
Dd is defined as the total length of streams per unit area divided by the area of drainage basin [51] . It refers to the closeness of spacing of channels, and it is therefore used as a measure of topographic dissection and runoff potential of a given watershed. High Dd value indicates high runoff, and consequently a low infiltration rate. By contrast, low drainage density of a basin implies low runoff and high infiltration [56] . Additionally, Strahler [39] argued that low Dd values are achieved when the basin relief is high and slopes are very steep. Other environmental factors controlling Dd are: infiltration capacity of the soil, and the resistance of underlying materials towards erosion. In poorly drained catchments, Dd values are in the range of 0.75 km/km2, or one fourth as great [51] . Drainage density values for the main river basin are 1.385, and for the sub-basins, it ranges from 1.19 to 1.77 which denotes moderate to well-drained catchments. Slight variation is observed in Dd values between the upper sub-basins ( = 1.43), and the lower sub-basins (
= 1.43), and the lower sub-basins (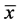 = 1.32). Higher drainage density in the upper watersheds may be attributed to the availability of rainfall, and the presence of high relief with steep slopes which resulted in greater runoff and more surface drainage lines [13] .
= 1.32). Higher drainage density in the upper watersheds may be attributed to the availability of rainfall, and the presence of high relief with steep slopes which resulted in greater runoff and more surface drainage lines [13] .
4.2.6. Drainage Texture (Dt)
Drainage texture (Dt) represents the relative channel spacing in a fluvially dissected topography. Dt refers to the total number of stream segments of all orders per perimeter of that basin [51] . It depends on a number of physical factors, such as lithology, relief, soil, vegetation, infiltration-capacity, climate, rainfall, and stage of drainage basin development. The Dt value for W. Wala is 1.7, and for the 23 sub-watersheds varies from 1.36 to 2.753. However, the variation in Dt values is slight between the upper sub-basins (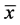 = 1.734). According to Smith [57] , the drainage texture for W. Wala and the sub-basins ranges from very coarse to coarse texture. It is postulated that high drainage texture values indicated the presence of fragile slope materials and soft rocks. Although the drainage intensity is low for W. Wala, the deterioration of vegetation cover, overgrazing, and high basin relief caused serious soil erosion, thus, high sediment yield was recorded recently [58] .
= 1.734). According to Smith [57] , the drainage texture for W. Wala and the sub-basins ranges from very coarse to coarse texture. It is postulated that high drainage texture values indicated the presence of fragile slope materials and soft rocks. Although the drainage intensity is low for W. Wala, the deterioration of vegetation cover, overgrazing, and high basin relief caused serious soil erosion, thus, high sediment yield was recorded recently [58] .
4.2.7. Basin Relief (Bh)
Basin relief (Bh) is the difference in elevation between the highest and the lowest point of a given watershed [59] . Bh parameter significantly controls stream gradient, thus, influencing flooding patterns, and the amount of sediments that can be transported. Basin relief in this regard, is a measure of the potential energy of the drainage system present by virtue of elevation above a given datum [60] . Thus, it is a fundamental factor in understanding the denudational status of a drainage basin, drainage network development, overland flow and through flow, and the fluvial-erosional characteristics of the terrain. The basin relief of W. Wala catchment is 1334 m, and for the 23 sub-watersheds it ranges from 96 m to 459 m (Table 2 and Table S1). High Bh values imply a high potential erosional energy of the drainage basin. As a result of progressive lowering of the Dead Sea base level, and tectonic uplifting, the wadi retained rapid down cutting and incision through its geomorphic history, giving rise to remarkable canyons (300 - 500 m of depth) downstream, dissected rough terrain in the lower reaches, interrupted valley-side slopes, and a noticeable rejuvenation stages (1, 2, 3, and 4 on Figure 7(b)) appearing on the superimposed and projected cross profiles (Figure 7(a) and Figure 7(b)). East of the Dead Sea, three slope categories (15˚ - 20˚, 20˚ - 30˚, >30˚) are dominated. Cliffs of >50˚, are also abundant downstream of W. Wala and along the Dead Sea escarpment. Further, most of the terrain here is confined between 700 m and 800 m contours. Nevertheless, high rates of annual soil loss and sediment yield are characteristic of W. Wala [58] , W. Mujib [61] and W. Kerak [62] just to the south of the present study area. High soil erosion loss and sediment load are indicative of active geomorphic processes at present.
Figure 7. (a) Superimposed and (b) projected cross profiles of W. Wala illustrate the four stages of rejuvenation east of the outlet.
4.2.8. Relief Ratio (Rr)
Relief ratio (Rr) is elaborated as a dimensionless height-length ratio between the basin relief (Bh) and the basin length (Lb) [59] . The Rr parameter allows comparison of the relative relief of any watershed regardless of differences in scale of topography. The relief ratio for W. Wala catchment is 15.1, and for the sub- watersheds it ranges from 8.485 to 76.1. Such values indicate high erosive power owing to the presence of steep gradients.
4.2.9. Ruggedness Number (Rn)
Ruggedness number (Rn) is a dimensionless parameter expressing the product of basin relief (Bh) and drainage density [39] [48] . The Rn parameter has been introduced to measure the flash flood potential of streams [63] , and is also employed to express the geometric characteristics of drainage basins [10] . High values of Rn are achieved when both parameters (Bh and Dd) are large, as exemplified by W. Wala and other Jordan Rift rivers, where slopes are not only steep but long as well. The ruggedness number for W. Wala is relatively high (1.82), and for the 23 sub-watersheds, it varies from 0.234 to 0.628. Consequently, W. Wala catchment is considered to be of pronounced morphology [45] . Watersheds having high Rn values are subjected to dynamic geomorphic processes, with long and steep slopes interrupted by sharp breaks of slope due to rejuvenation. Further, the catchment is of high susceptibility to soil erosion, sediment load production, mass movements, and of high response to an as increase in peak discharge.
4.2.10. Hypsometric Integral (HI)
Hypsometric analysis refers to the relative proportion of an area at different elevations of the earth’s surface [64] . This approach has been developed to interpret the geomorphic stage of landscape development, denudational processes acting over drainage basins, and to analyze and explain the impact of tectonic activity over a region. The hypsometry of a drainage basin can be evaluated graphically through the “hypsometric curve” (HC) and quantitatively as an integral termed “hypsometric integral” (HI) which are both analyzed with reference to the degree of drainage basin dissection and the relative age landforms. Thus, hypsometric analysis is essential for establishing the relative age of landforms. Consequently, hypsometric analysis is essential tool to assess the impact of lithology, tectonics and climate on landform change, and to evaluate the interaction between tectonic uplift and erosion over an area or watershed. The hypsometric curve represents the volume of rock mass in the watershed against the remaining mass [65] [66] [67] , whereas, the hypsometric integral is calculated from the area under a hypsometric curve and expressed as a percentage, where its value varies from 0 to 1 [68] . The hypsometric curves of W. Wala and the 10 sub-watersheds selected for the purpose of further analysis are convex upward, which is indicative of the youth-age stage of geomorphic development. Two categories of hypsometric integrals are identified. The values of the first category range from 85% to 89%, and represent the rejuvenated belt (Figure 8) characterizing the western part of the watershed. Whereas, the second category describes the HI values which vary from 70% to 84% and pertained to the eastern zone of the watershed (Figure 8) which is less impacted by rejuvenation. Elongation ratio (Re) is defined as the ratio between the diameter of a circle of the same area as the basin area (A) and basin length (Lb) [59] . Strahler [39] claimed that the values of Re range from 0.6 to 1.0 over a wide range of geological and environmental conditions.
4.3. Shape Morphometric Parameters
4.3.1. Elongation Ratio (Re)
Values close to 1.0 are characteristic of areas with very low relief, while values in the range of 0.6 to 0.8 are typical of drainage basins with high relief and steep slopes. Low values of Re denote that basins are more elongated, and whenever values approach 1.0, the shape of drainage basin approaches a circle [59] . A circular basin is more efficient in runoff than is an elongated one [69] . The elongation
Figure 8. Hypsometric integral categories characterized the rejuvenated belt and eastern zone.
ratio of W. Wala is 0.577, and for sub-watersheds, it ranges from 0.475 to 1.0 (one sub-basin is only circular), which implies that most of the sub-basin are more elongated and elongated in shape.
4.3.2. Circularity Ratio (Rc)
The circularity ratio is defined as the ratio of the basin area (A) and the area of a circle with the same perimeter (P) as that of the basin [39] . Rc is controlled by the length and frequency of the streams, lithology and structure, land use/ cover, climate, relief and slope for streams of different orders. The Rc parameter is indicative of basin shape, the rate of infiltration, and the time needed for the excess water to reach the basin outlet. Miller [70] described drainage basins of different circularity ratios ranging from 0.4 to 0.5 and concluded that they are strongly elongated, with homogeneous geological materials, and a uniform rate of infiltration; therefore, the excess runoff takes a longer time to reach the basin outlet. Further, low, medium and high values of Rc imply the young, mature, and old stage of the geomorphic cycle of the catchment. The Rc value of W. Wala is 0.159 and for the 23 sub-basins ranges from 0.067 to 0.469. These low values generally indicate that the watershed and the sub-watersheds are at the youth stage of geomorphic evolution, which resembles other Jordan Rift watersheds [68] .
4.3.3. Form Factor (Rf)
The form factor (Rf) is defined as the ratio between the area of the basin (A) and the square of the basin length (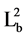 ). It was elaborated by Horton (1945) to predict the flow intensity of a drainage basin of a defined area. It reveals an inverse relationship with square of the axial length and a direct relation with peak discharge [37] . For a perfectly circular basin, the value of Rf should always be <0.75 [12] . The smaller the value of form factor (<0.45), the more the basin will be elongated. Watersheds with high Rf values experience high peak flows of short duration. By contrast, an elongated watershed with low form factor, has a low peak flows of longer duration. The Rf value for W. Wala is 0.268, and for the 23 sub-basins it ranges from 0.086 to 0.81, which indicates that the sub-basins are often elongated basins; consequently, low peak flows of long duration predominate [3] .
). It was elaborated by Horton (1945) to predict the flow intensity of a drainage basin of a defined area. It reveals an inverse relationship with square of the axial length and a direct relation with peak discharge [37] . For a perfectly circular basin, the value of Rf should always be <0.75 [12] . The smaller the value of form factor (<0.45), the more the basin will be elongated. Watersheds with high Rf values experience high peak flows of short duration. By contrast, an elongated watershed with low form factor, has a low peak flows of longer duration. The Rf value for W. Wala is 0.268, and for the 23 sub-basins it ranges from 0.086 to 0.81, which indicates that the sub-basins are often elongated basins; consequently, low peak flows of long duration predominate [3] .
5. Results and Discussion
ASTER DEM was employed for morphometric analysis of a progressive rejuvenated Rift watershed draining to the Dead Sea, the lowest base level worldwide. Although STRM DEM facilitates more accurate information regarding elevation, ASTER DEM (30 m spatial resolution) provides better morphometric, geomorphic and geological details [71] . Further, ASTER DEM is provided on line cost- free, and is available in Geo Tiff format, with geographic latitude/longitude coordinates at a 1 arc-second, approximately 30 m grid cell size (ASTER DEM Validation Team 2011). Consequently ASTER DEM has been utilized in watershed morphometry, management, prioritization of soil and water measures, and assessment of flash flood risks in arid and semi-arid watersheds [16] [18] [19] [24] [25] [72] [73] . The use of the ASTER DEM and GIS software package enables rapid, precise, and inexpensive tools to extract and analyze morphometric parameters for W. Wala and the 23 sub-watersheds. Rb values of stream order I is higher than those of stream order II and III (Table S1). Rb values fall in the range of 2 - 5 except for sub-basins nos. 5, 12, 13, and 15 where the bifurcation ratio in streams order II and III reached 7, this due to structural control and the presence of steep slopes. High Rb values generally reflects continuous Rift disturbance which caused progressive uplifting, NE tilting, continuous lowering of the Dead Sea base level, and rejuvenation, and consequently recurrent headward erosion and river incision. Additionally, the total number of streams of order I are high for sub-basins nos. 4, 5, 12, 13, 19, 20, and for streams of order II (sub-watersheds nos. 5, 12, and 13) are high as well (Figure 9(a)) compared to order III. All these sub-basins are located at the northeastern, eastern, and southeastern part of W. Wala watershed, which are affected enormously by uplifting and tilting. Further, all these sub-watersheds are confined between 800 m and 900 contours, and in the southeastern part of the watershed they are restrained between 700 m and 800 m contours. The dominance of steep slopes and topographic conditions favor rapid erosion and the initiation of an integrated drainage network with total high stream numbers. The minimum and maximum stream length (Lu) km, are higher for the streams of order I (69 to 265 km) than streams of order II (25 to 71 km), and streams of order III (13 to 38 km). Similarly, the spatial distribution of sub-basins of first-order, second-order and third-order are relatively the same of the distribution of sub-basins in terms of the total number of streams with respect to their order (Figure 9(b)).
Figure 9. (a) The number of streams, and (b) stream lengths in relation to stream order.
Regression analysis was performed to explore the physical behavior and interrelations between morphometric variables in arid and semi-arid W. Wala and the 23 sub-watersheds. Figures 10(a)-(h) illustrates the results of regression analysis between basin area (A) as an independent parameter on the horizontal axis, and other variables (total stream length(km), stream frequency (Fs), perimeter (P) km, basin length (Lb) km, circularity ratio (Rc), elongation ration (Re), basin relief (Bh) m, and log cumulative mean stream length) as dependent para-




Figure 10. (a)-(h) Interrelations between morphometric parameters (A vs. P, Lb, Rc, Re, and Bh), (Dd, vs. Fs), and (u vs. log cumulative Lsm).
meters on the vertical axis. Parameters such as total stream length (R2 = 0.991), perimeter (R2 = 0.865), basin length (R2 = 704), and log cumulative mean stream length (R2 = 0.997) have direct proportional strong regression relations with basin areas, whereas stream frequency (R2 = 0.184), and basin relief (R2 = 0.54), and elongation ratio (R2 = 0.126) have an indirect relation with basin areas, and a weak to moderate relationship. The degree of correlation between basin areas and other parameters is displayed in Figures 10(a)-(h).
Stream length ratio (RL) is an indicator of the relative hydrological properties, i.e., permeability of the underlying rocks, sediment load, and soil erosion rates over a watershed. Thus, it is considered an important parameter in relation to water discharge and erosional stage of a catchment [21] [74] . A statistical evaluation of stream length ratio was implemented and the results are illustrated in Table 3. The Table shows that RL values estimated between the first and the second steam order accommodate all RL ratio categories. Then RL values diminished for sub-basins when RL values were estimated between the second and third stream orders, and between the third and fourth stream orders. Four categories of RL values have been observed in II/I orders; three categories RL ratios presented in III/II orders, and two categories of RL ratios existed in IV/III only. The higher values of RL values indicate the young geomorphic landforms development across the watershed [13] . Moreover, the highest minimum and maximum lengths characterize stream order I (Figure 9(b)), and the moderate minimum and maximum lengths are realized in stream order II, while small minimum and maximum lengths are observed in stream order III. Furthermore, the highest minimum and maximum stream numbers are available in stream order I. The moderate minimum and maximum stream numbers are realized in stream order II, and the small minimum and maximum stream numbers are observed in stream order III (Figure 9(a)). Sub-watersheds nos. 1, 3, 5, 6, 8, 10, 11, and 12 reveal an average Rr value of 19.12. The Rr values explain the intensity of the stream channel gradient, therefore, it is an important factor in assessing erosion processes, soil loss rates and sediment load. Consequently, the peak of discharge and runoff intensity can be predicted [21] . Further, the western sub?watersheds have a higher mean slope, thus providing favorable topographic conditions for a
Table 3. Statistical evaluation of stream length ratio (RL).
high rate of hillslope processes. Ruggedness number (Rn) parameter shows appreciable variation between the eastern sub-basins and the western sub-water- sheds. The average Rn values for the eastern sub-basins (1, 2, 3, 4, 5, 8, 10, 11, 12 and 13) is 0.36, whereas the average Rn values for the western sub-basins, or the rejuvenation belt (9, 14, 16, 17, and 18) is 0.46. Lower Rn values in the upper watershed imply high eroded surfaces, and higher Rn values of the sub-basins downstream denote higher flash flood potential. Extensive variation in circularity ratios (Rc) exists between sub-basins of the rejuvenation belt, and sub-water- sheds of the eastern zone. The average Rc value for the western sub-basins (7, 9, 14, 16, 18, 21, 22, and 23) is 0.314, or more elongated in shape. By contrast, the Rc average value for sub-basins of the eastern sector (1, 2, 3, 4, 5, 12, 13, 17, 19, and 20) is 0.182, which indicated that all sub-basins are elongated, or have less circular shape. Thus, low discharge of runoff, and delayed time to peak flow are expected. Elongated sub-basins can be realized in the eastern zone of W. Wala watershed, where the average Re is 0.56, and the average Re for the western sub-watersheds is 0.701, which indicates less elongated sub-watersheds. The dominance of elongated sub-basins in the eastern zone is a reflection of the faults identified in the watershed. The large number of streams related to stream order I and II, and the highest stream length pertained to stream of order I and II are found particularly in the middle and upper reaches of W. Wala watershed and the associated sub-watersheds due to the presence of dense lineaments, uplifting, and NE tilting of the catchment. Fs values show appreciable variation from the western part of the catchment to the east, and the trend generally increase from the lower to the upper reaches of the catchment. The average Fs value for the eastern sub-watersheds (i.e., sub-watersheds nos. 5, 6, 8, 10, 11, and 12) is 1.43, whereas the average Fs value for the western sub-watersheds (i.e., sub-watersheds nos. 14, 15, 16, 18, 21, 22, and 23) is 1.39. The response of the sub-basins in the rejuvenated zone towards subsidence of the Jordan Rift (and continuous lowering of the Dead Sea base level) was directed to downstream incision rather than development and increase of stream number in the middle and upper reaches. Stream incision is facilitated by dense lineaments, tilting and slope steepness. Variation in Fs values is dependent mainly on tectonics, structure, lithology, and morphology (relief and slope). High values of Fs which characterize the north eastern, and south eastern sub-basins coincide reasonably well with high elevations (700 - 800 m, and 800 - 900 m). By contrast, lower Fs values are associated with sub-basins where the dominant slope categories are: 20˚ - 30˚ and >30˚ downstream the watershed. Here, physical conditions suggest increased runoff and decreased infiltration rates, hence making these sub-basins more susceptible to flooding, landslide activity, and surface erosion.
A remarkable variation in relief ratio (Rr) values exists in the 23 sub-basins of W. Wala. The western sub-basins (i.e., sub-watersheds nos. 9, 14, 16, 17, 18, 21, 22, and 23) show an average Rr value of 30.5. Northern, eastern, and southern sub-basins are characterized by lower Rf values compared with western sub- basins (where 
It is argued that high HI values are correlated to youth-stage of geomorphic development, and active tectonics, while, low HI values are related to old degraded landscapes that have been more eroded and less impacted by neo-tec- tonics and recent tectonic activity [75] . Average HI values for the entire W. Wala, the rejuvenated belt sub-basins, and the eastern zone sub-basins are: 81%, 84%, and 79% respectively. High HI values generally denote that these drainage basins are tectonically uplifted and tilted NE, and thus hillslope processes predominate. To evaluate the interactive relationship between driving morphometric parameters and HIs, or specifically, to examine the degree of control of the following parameters (sub-basin area (km2), height of local base level (m), mean height of sub-basin (m), slope (degrees), elongation ratio, and form factor) over hypsometric integral values. Regression analysis reveals that R2 values (Figures 11(a)-(f)) are positive and generally low (0.003 - 0.0056), except for the height of local base level (m) which accounts for 0.42 (F-value is significant at 0.1% level), and for the mean height of the sub-basin which contributes 0.39. It is noticeable that the height of local base level (m), and mean height (m) of sub-basins have a significant control on HI, whereas, other driving parameters show a weak relationship, indicating negligible control over HI values. Thus, the 42 percent of variation in HI is explained by the recognized predictor parameters (the height of base level (m) and mean height (m) of sub-basins.
5. Conclusions
The present study verifies the efficiency of remote sensing data (ASTER DEM) and Arc GIS tool for hydro-morphometric analysis at sub-watershed level for W. Wala, a rejuvenated rift catchment. Morphometric analysis was employed to compute basic, derived, and shape parameters of the entire watershed and the 23 sub-watersheds. A strong relationship has been identified between stream order (u), stream number (Nu), and stream length (Lu), and a nearly straight line was established which depicts the flow direction of channels from higher elevation (700 m - 800 m, and 800 m - 900 m) to low elevations towards the canyon-shape and V-shaped downstream. Rb values are high, where it ranges between 2 and 7, thus suggesting structural control over the drainage network. The total number of streams of order I is higher than order III due to uplifting, tilting, and topographic factors (steep slopes and high relief). Higher Dd values in the upper sub-basins (






Figure 11. (a)-(f) Regression models between the HIs values and different driving factors (elongation ratio (a), form factor (b), basin area (c), height of local base level (d), mean height (e), and slope (f)).
changes) prior to the upper sub-watersheds. Most of the drainage basins in the eastern part of the watershed are elongated or less elongated, thus, it can predict that they are characterized by smaller flood peaks and long flow path. Due to deterioration of vegetation cover, all sub-basins have a high potential to soil erosion and sediment yield encouraged by morphological factors (relief and steep slopes), and the availability of rainfall factors. Rf value for the entire watershed is 0.268, and the values for the 23 sub-basins range from 0.18 to 0.81. Low Rf values indicate that the basins are elongated or less elongated, thus, low discharge, or runoff is characteristic and delay time to peak flow is expected. High relief ratio (Rr) is observed for several sub-basins in the rejuvenated belt, or the western part of the catchment (sub-basins nos. 9 [23.9], 14 [38.3], 16 [76.0], 18 [31.2], 23 [24.5], and sub-watersheds of the eastern sector (sub-basins nos. 1 [21.4], 6 [16.0], 10 [32.69], 11 [23.2], can be considered an important factor in the evaluation of soil erosion and sediment load in W. Wala catchment. Consequently, the peak of discharge and runoff intensity can be predicted. The hypsometric curves for W. Wala catchment and the ten sub-watersheds are of convex upward shape, which is indicative of a youth-age stage of geomorphic development. The calculated hypsometric integral values for the western sub- basins (the rejuvenated belt) vary from 85.0% to 89.0%. By contrast, HI values for the eastern sector sub-basins range from 70% to 84.0%. High HI values indicate that these drainage basins are affected by tectonic activity, uplifting, and active hill-slope processes. Low HI values can be interpreted that the eastern basins are extend 30 - 50 km east of the main base level, and thus they are less impacted by rejuvenation processes compared to the western sub-watersheds. The degree of control of driving morphometric parameters over HI values was assessed using regression analysis. The results show that R2 values (which represent the degree of control of driving parameters over HI) are generally low, except for the height of local base level (m) parameter which accounts for 0.42 (F-value is significant at 0.1% level), and for the mean height (m) variables of sub-basins which contributes 0.39. It is perceptible that the height of local base level (m) and the mean height (m) of sub-basins have a significant control over HI. The development of the stream segments, and the elongated shape of the sub-watersheds are attributed to tectonic and structure, and to morphological controls. The recognized fault groups and the resultant dense lineaments, high slope and relative relief contribute to an overall variation in morphometric and hydrological properties of sub-basins drainage (i.e., runoff and infiltration, soil erosion, landslide activity, sediment load, and flooding). Furthermore, the shape parameters resulted in elongated or less elongated sub-watersheds with low flood peaks and longer flood flows. Flood characteristics, soil erosion rates, and recently recorded high sediment load are considered intrinsic factors in watershed management, rural land use planning, range management, prioritization of sub-basins for soil and water conservation measures, and flood risk assessment.
Cite this paper
Yahya Farhan (2017) Morphometric Assessment of Wadi Wala Watershed, Southern Jordan Using ASTER (DEM) and GIS. Journal of Geographic Information System, 9, 158-190. https://doi.org/10.4236/jgis.2017.92011
References
- 1. Chorely, R. (1971) The Drainage Basin as the Fundamental Geomorphic Unit. In: Chorely, R., Ed., Introduction to Fluvial Processes, Methuen and Co. Ltd., London, 30-32.
- 2. Sreedevi, P.D., Owais S., Khan, H.H. and Almed, S. (2009) Morphometric Analysis of Watershed of South India Using SRTM Data and GIS. Journal of the Geological Society of India, 73, 543-552.
https://doi.org/10.1007/s12594-009-0038-4 - 3. Magesh, N.S., Chandrasekar, N. and Soundranayagam, J.P. (2011) Morphometric Evaluation of Papanasam and Manimuthar Watersheds, Part of Western Ghats. Tirunelueli District, Tamil Nadu, India: A GIS Approach. Environmental Earth Sciences, 64, 374-381.
https://doi.org/10.1007/s12665-010-0860-4 - 4. Hlaing, K., Haruyama, S. and Aye, M. (2008) Using GIS based Distributed Soil Loss Modeling and Morphometric Analysis to Prioritize Watersheds for Soil Conservation in Bago River Basin of Lower Myanmar. Frontiers of Earth Science in China, 2, 465-478.
https://doi.org/10.1007/s11707-008-0048-3 - 5. Patel, D., Dholakia, M., Naresh, N. and Srivastava, P. (2012) Water Harvesting Structure Positioning by Using Geo–Visualization Concept and Prioritization of Mini–Watersheds through Morphometric Analysis in the Lower Tapi Basin. Journal of the Indian Society of Remote Sensing, 40, 299-312.
https://doi.org/10.1007/s12524-011-0147-6 - 6. Patel, D., Gajjar, C. and Srivastava, P. (2013) Prioritization of Malesari Mini-Watersheds through Morphometric Analysis: A Remote Sensing and GIS Perspective. Environmental Earth Sciences, 69, 2643-2656.
https://doi.org/10.1007/s12665-012-2086-0 - 7. Clark, J. (1965) Morphometry from Maps. In: Dury, G.H., Ed., Essays in Geomorphology. Heinemann, London, 235-274.
- 8. Mesa, L.M. (2006) Morphometric Analysis of a Subtropical Andean Basin (Tucuma’n, Argentina). Environmental Geology, 50, 1235-1242.
https://doi.org/10.1007/s00254-006-0297-y - 9. Thomas, J., Joseph, S., Thrivikramji, K., Abe, G. and Kannan, N. (2012) Morphometric Analysis of Two Tropical River Basins of Contrasting Environmental Settings, the Southern Western Ghats, India. Environmental Earth Sciences, 66, 2353-2366.
https://doi.org/10.1007/s12665-011-1457-2 - 10. Sujatha, E., Selvakumar, R., Rojasimman, U. and Victor, R. (2013) Morphometric Analysis of Sub-Watersheds in Parts of Western Ghats, South India Using ASTER DEM. Geomatics, Natural Hazards and Risk, 6, 326-341.
https://doi.org/10.1080/19475705.2013.845114 - 11. Yanina, M., Esper, A. and Perucca, L.P. (2014) Geomorphology and Morphometry of the de La Flecha River Basin, San Juan, Argentina. Environmental Earth Sciences, 72, 3227-32337.
https://doi.org/10.1007/s12665-014-3227-4 - 12. Chopra, R., Dhiman, R.D. and Sharma, P.K. (2005) Morphmetric Analysis of Sub-Watersheds in Gurdaspur District, Punjab Using Remote Sensing and GIS Techniques. Journal of the Indian Society of Remote Sensing, 33, 350-361.
https://doi.org/10.1007/BF02990738 - 13. Kaliraj, N., Chandrasekar, N. and Magesh, S. (2015) Morphometric Analysis of the River Thamirabarani Sub-Basin in Kanya Kumari District, South West Coast of Tamil Nadu, India, Using Remote Sensing and GIS. Environmental Earth Sciences, 73, 7375-7401.
https://doi.org/10.1007/s12665-014-3914-1 - 14. Arnous, M., Aboulela, H. and Green D. (2011) Geo-Environmental Hazards Assessment of the North Western Gulf of Suez, Egypt. Journal of Coastal Conservation, 15, 37-50.
https://doi.org/10.1007/s11852-010-0118-z - 15. Youssef, A., Pradhan, B. and Hassan, A. (2011) Flash Flood Risk Estimation along the St. Katherine Road, Southern Sinai, Egypt Using GIS Based Morphometry and Satellite Imagery. Environmental Earth Sciences, 62, 611-623.
https://doi.org/10.1007/s12665-010-0551-1 - 16. Youssef, A., Pradhan, B. and Sefry, S. (2016) Flash Flood Susceptibility Assessment in Jeddah City (Kingdom of Saudi Arabia) Using Bivariate and Multivariate Statistical Models. Environment Earth Sciences, 75, 12.
https://doi.org/10.1007/s12665-015-4830-8 - 17. Abdel-Lattif, A. and Sherief, Y. (2012) Morphometric Analysis of Flash Floods of Wadi Sudr and Wadi Wardan, Gulf of Suez, Egypt: Using Digital Elevation Model. Arab Journal of Geosciences, 5, 181-195.
https://doi.org/10.1007/s12517-010-0156-8 - 18. Masoud, M. (2016) Geoinformatics Application for Assessing the Morphometric Characteristics' Effect on Hydrological Response at Watershed (Case Study of Wadi Qanunah, Saudi Arabia). Arabian Journal of Geosciences, 9.
- 19. Kusre, B. (2016) Morphometric Analysis of Diyung Watershed in Northeast India Using GIS Technique for Flood Management. Journal of the Geological Society of India, 87, 361-369.
https://doi.org/10.1007/s12594-016-0403-z - 20. Asode, A., Sreenivasa, A. and Lakkundi, T. (2016) Quantitative Morphometric Analysis in the Hard Rock Hirehalla Sub-Basin, Bellary and Davanagere District, Karnataka, India Using RS and GIs. Arabian Journal of Geosciences, 9, 381.
- 21. Al-Saady, Y., Al-Suhail, Q., Al-Tawash, B. and Othman, A. (2016) Drainage Network Extraction and Morphometric Analysis Using Remote Sensing and GIS Mapping Techniques (Lesser Zab River Basin, Iraq and Iran). Environmental Earth Sciences, 75, 1243.
- 22. Biswas, S., Sudhakar, S. and Desai, V. (1999) Prioritization of Sub-Watersheds Based on Morphometric Analysis of Drainage Basin: A Remote Sensing and GIS Approach. Journal of the Indian Society of Remote Sensing, 27, 155-166.
https://doi.org/10.1007/BF02991569 - 23. Javed, A., Khanday, M. and Ahmad, R. (2009) Prioritization of Sub-Watersheds Based on Morphometric and Land Use Analysis in Guna District (M.P.): A Remote Sensing and GIS Based Approach. Journal of the Indian Society of Remote Sensing, 37, 261-274.
https://doi.org/10.1007/s12524-009-0016-8 - 24. Khanday, M. and Javed, A. (2016) Prioritization of Sub-watersheds for Conservation Measures in a Semi Arid Watershed Using Remote Sensing and GIS. Journal of the Geological Society of India, 88, 185-196.
https://doi.org/10.1007/s12594-016-0477-7 - 25. Makwana, J. and Tiwari, M. (2016) Prioritization of Agricultural Sub-Watersheds in Semi Arid Middle Region of Gujarat Using Remote Sensing and GIS. Environmental Earth Sciences, 75, 1-12.
https://doi.org/10.1007/s12665-015-4935-0 - 26. Farhan, Y. and Anaba, O. (2016) Watershed Prioritization Based on Morphometric Analysis and Soil Loss Modeling in Wadi Kerak (Sourthern Jordan) Using GIS Techniques. International Journal of Plant and Soil Science, 10, 1-18.
https://doi.org/10.9734/IJPSS/2016/25321 - 27. Farhan, Y. and Anaba, O. (2016b) A Remote Sensing and GIS Approach for Prioritization of W. Shueib Mini-Watersheds (Central Jordan) Based on Morphometric and Soil Erosion Susceptibility Analysis. Journal of Geographic Information System, 8, 1-19.
https://doi.org/10.4236/jgis.2016.81001 - 28. Sarp, G. and Duzgun, S. (2015) Morphometric Evaluation of the Afsin-Elbistan Lignite Basin Using Kernel Density Estimation and Getis-Ord's Statistics of DEM Derived Indices, SE Turkey. Journal of Asian Earth Sciences, 111, 819-826.
- 29. Gürbüz, E., Kazanic, N. and Gürbüz, A. (2015) Strike-Slip Faulting, Topographic Growth and Block Movements as Deduced From Drainage Anomalies: The Yesilirmak River Basin, Northern Turkey. Geomorphology, 246, 634-648.
- 30. Jacques, P., Salvador, E., Machado, R., Grohmann, C. and Nummer, A. (2014) Application of Morphometry in Neotectonic Studies at the Eastern Edge of the Parana Basin, Santa Catarina State, Brazil. Geomorphology, 213, 13-23.
- 31. Markose, V. and Jayappa, K. (2013) A Quantitative Analysis of Relative Tectonic Activity Classes of Kali River Basin, Southwest Coast of India. Arabian Journal of Geosciences, 6, 4729-4742.
https://doi.org/10.1007/s12517-012-0719-y - 32. Roy, S. and Sahu, A. (2016) Morphotectonic Map Generation Using Geo-Informatics Technology: Case Study over the Ajay-Damodar Interfluve, West Bengal, INDIA. Arabian Journal of Geosciences, 9, 183.
- 33. Manu, M. and Anirudhan, S. (2008) Drainage Characteristics of Achankovil River Basin, Kerla. Journal of the Geological Society of India, 71, 841-850.
- 34. Yanina, M., Esper Angillieri, M.Y. and Perucca, L. (2015) A Large and Active Debris-Rockslide in the Central Andes of Argentina (30.26°S): Morphometry and Triggering Mechanisms. Quaternary International, 374, 182-188.
- 35. Frissel, C., Liss, W., Warren, C. and Hurley, M. (1986) A Hierarchical Framework for Stream Habitat Classification: Viewing Streams in a Watershed Context. Environmental Management, 10, 199-214.
https://doi.org/10.1007/BF01867358 - 36. Subyani, A., Qari, M. and Mastah, M. (2012) Digital Elevation Model and Multivariate Statistical Analysis of Morphometric Parameters of Some Wadis, Western Saudi Arabia. Arabian Journal of Geosciences, 5, 147-157.
https://doi.org/10.1007/s12517-010-0149-7 - 37. Gregory, K. and Walling, D. (1973) Drainage Basin Form and Process: A Geomorphological Approach. Wiley, New York.
- 38. Esper Angillieri, M.Y. (2008) Morphometric Analysis of Colanguil River Basin and Flash Flood Hazard, San Juan, Argentina. Environmental Geology, 55, 107-111.
https://doi.org/10.1007/s00254-007-0969-2 - 39. Strahler, A. (1964) Quantitative Geomorphology of Drainage Basins and Channel Networks. In: Chow, V., Ed., Handbook of Applied Hydrology, McGraw-Hill, New York, 439-476.
- 40. Vieceli, N., Bortolin, T., Mendes, L., Bacarim, G., Cemin, G. and Schneider, B. (2015) Morphometric Evaluation of Watersheds in Caxias do Sul City, Brazil, Using SRTM(DEM)Data and GIS. Environmental Earth Sciences, 73, 5677-5685.
https://doi.org/10.1007/s12665-014-3823-3 - 41. Bender, F. (1975) Geology of the Arabian Peninsula: Jordan. United States Geological Survey Professional Paper 560-I, Washington DC.
- 42. McDonald Partners and Hunting Technical Services Ltd. (1965) East Bank Water Resources Summary Report. Central Water Authority, Amman.
- 43. Al-Bakri, J. and Al-Jahmany, Y. (2013) Application of GIS and Remote Sensing to Groundwater Exploration in Al-Wala Basin in Jordan. Journal of Water Resources and Protection, 5, 962-971.
https://doi.org/10.4236/jwarp.2013.510099 - 44. Farhan, Y. (1982) Slope Morphology in Central Jordan. Yarmouk University Press, Irbid. (In Arabic)
- 45. Farhan, Y., Anbar, A., Enaba, O. and Al-Shaikh, N. (2015) Quantitative Analysis of Geomorphometric Parameters of Wadi Kerak, Jordan, Using Remote Sensing and GIS. Journal of Water Resources and Protection, 71, 456-475.
https://doi.org/10.4236/jwarp.2015.76037 - 46. Chorely, R. (1958) Aspects of the Morphometry of “Poly-Cyclic” Drainage Basin. The Geographical Journal, 124, 370-374.
https://doi.org/10.2307/1790789 - 47. Farhan, Y., Elgaziri, A., Elmaji, I. and Ali, I. (2016) Hypsometric Analysis of Wadi Mujib-Wala Watershed (Southern Jordan) Using Remote Sensing and GIS Techniques. International Journal of Geosciences, 7, 158-176.
https://doi.org/10.4236/ijg.2016.72013 - 48. Strahler, A. (1952) Hypsometric (Area-Altitude) Analysis of Erosional Topography. Geological Society of America Bulletin, 63, 1117-1141.
https://doi.org/10.1130/0016-7606(1952)63[1117:HAAOET]2.0.CO;2 - 49. Strahler, A. (1957) Quantitative Analysis of Watershed Geomorphology. Transactions, American Geophysical Union, 38, 913-920.
https://doi.org/10.1029/TR038i006p00913 - 50. Chorely, R., Donald, M. and Pogrzelski, H. (1957) A New Standard for Estimating Drainage Basin Shape. American Journal of Science, 255, 138-141.
https://doi.org/10.2475/ajs.255.2.138 - 51. Horton, R. (1945) Erosional Development of Streams and their Drainage Basins; Hydrophysical Approach to Quantitative Morphology. Geological Society of America Bulletin, 56, 275-370.
https://doi.org/10.1130/0016-7606(1945)56[275:EDOSAT]2.0.CO;2 - 52. Chow, V. (1964) Applied Hydrology. McGraw Hill, New York.
- 53. Verstappen, H. (1983) Applied Geomorphology: Geomorphological Surveys for Environmental Development. Elsevier, New York.
- 54. Sreedevi, P., Sreekanth, P., Khan, H. and Ahmed, S. (2013) Drainage Morphometry and Its Influence on Hydrology in an Semi Arid Region: Using SRTM Data and GIS. Environmental Earth Sciences, 70, 839-848.
https://doi.org/10.1007/s12665-012-2172-3 - 55. Melton, M. (1957) An Analysis of the Relations Among Elements of Climate, Surface Properties and Geomorphology. Department of Geology, Columbia University, Technical Report, 11, Project NR 389-042. Office of Navy Research, New York.
- 56. Prasad, R., Mondal, N., Banerjee, P., Nandakumar, M. and Singh, V. (2008) Deciphering Potential Groundwater Zone in Hard Rock through the Applicationi of GIS. Environmental Geology, 55, 467-475.
https://doi.org/10.1007/s00254-007-0992-3 - 57. Smith, K. (1950) Standards for Grading Textures of Erosional Topography. American Journal of Science, 248, 655-668.
https://doi.org/10.2475/ajs.248.9.655 - 58. Ijam, A. and Tarawneh, E. (2012) Assessing of Sediment Yield for Wala Dam Catchment Area in Jordan. European Water, 38, 43-58.
- 59. Schumm, S. (1956) Evolution of Drainage Systems and Slopes in Badland at Perth Amboy, New Jersey. Geological Society of America Bulletin, 67, 597-646.
https://doi.org/10.1130/0016-7606(1956)67[597:EODSAS]2.0.CO;2 - 60. Hadley, R. and Schumm, S. (1961) Sediment Sources and Drainage Basin Characteristics in Upper Cheyenne River Basin. US Geological Survey Water-Supply Paper 1531-B, Washington DC, 198.
- 61. Ijam, A. and Al-Mahamid, M. (2012) Predicting Sedimentation at Mujib Dam Reservoir in Jordan. Jordan Journal of Civil Engineering, 6, 448-463.
- 62. Farhan, Y. and Nawaysa, S. (2015) Spatial Assessment of Soil Erosion Risk Using RUSLE and GIS Techniques. Environmental Earth Sciences, 74, 4649-4669.
https://doi.org/10.1007/s12665-015-4430-7 - 63. Patton, P. and Baker, V. (1976) Morphometgry and Floods in Small Drainage Basins Subject of Diverse Hydrogeomorphic Controls. Waters Resources Research, 12, 941-952.
https://doi.org/10.1029/WR012i005p00941 - 64. Strahler, A. (1952b) Dynamic Basis of Geomorphology. Geological Society of America Bulletin, 63, 923-938.
https://doi.org/10.1130/0016-7606(1952)63[923:DBOG]2.0.CO;2 - 65. Hurtrez, J., Sol, C. and Lucazeau, F. (1999) Effect of Drainage Area on Hypsometry from Analysis of Small Scale Drainage Basins in the Siwalik Hills (Central Nepal). Earth Surface Processes and Landforms, 24, 799-808.
https://doi.org/10.1002/(SICI)1096-9837(199908)24:9<799::AID-ESP12>3.0.CO;2-4 - 66. Bishop, M., Shroder, J., Bonk, R. and Olsenholler, J. (2002) Geomorphic Change in High Mountains: A Western Himalayan Perspective. Global Planetary Change, 32, 311-329.
- 67. Harrison, C., Miskell, K., Brass, G., Saltzman, E. and Sloan II, J. (1983) Continental Hypsography. Tectonics, 2, 357-377.
https://doi.org/10.1029/TC002i004p00357 - 68. Farhan, Y., Mousa, R., Dagara, A. and Shtaya, D. (2016) Regional Hypsometric Analysis of the Jordan Rift Drainage Basins (Jordan) Using Geographic Information System. Open Journal of Geology, 6, 1312-1343.
https://doi.org/10.4236/ojg.2016.610096 - 69. Singh, S. and Sing, M.C. (1997) Morphometric Analysis of Kanhar River Basin. National Geographical Journal of India, 43, 31-43.
- 70. Miller, V. (1953) A Quantitative Geomorphic Study of Drainage Basin Characteristics in the Clinch Mountain Area, Virginia and Tennessee. Project NR 389-402, Technical Report 3, Columbia University, Department of Geology, ONR, New York.
- 71. Farhan, Y., Anaba, O. and Salim, A. (2016) Morphometric Analysis and Flash Floods Assessment for Drainage Basing of the Ras En Naqb Area, South Jordan Using GIS. Journal of Geosciences and Environmental Protection, 4, 4-33.
- 72. Aher, P., Adinarayana, J. and Gorantwar, S. (2014) Quantification of Morphometric Characterization and Prioritization for Management Planning in Semi-Arid Tropics of India: A Remote Sensing and GIS Approach. Journal of Hydrology, 511, 850-860.
- 73. Gopinath, G., Nair, A., Ambili, G. and Swetha, T. (2016) Watershed Prioritization Based on Morphometric Analysis Coupled with Multi Criteria Decision Making. Arabian Journal of Geosciences, 9, 129-146.
https://doi.org/10.1007/s12517-015-2238-0 - 74. Magesh, N. and Chadrasekar, N. (2014) GIS-Model-Based Morphometric Evaluation of Tamiraparani Subbasin, Tirunelveli District, Tamil Nayd, India. Arabian Journal of Geosciences, 7, 131-141.
https://doi.org/10.1007/s12517-012-0742-z - 75. El Hamdouni, R., Irigaray, C., Fernandes, T., Chacon, J. and Keller, E. (2007) Assessment of Relative Tectonics, Southwest Border of Sierra Nevada (Southern Spain). Geomorphology, 96, 150-177.
Appendix(I)
Table S1. Morphometric characteristics of the 23 sub-watersheds of Wadi Wala.

















