Journal of Geographic Information System
Vol.06 No.06(2014), Article ID:52159,16 pages
10.4236/jgis.2014.66053
Spatial Effects of Varying Model Coefficients in Urban Growth Modeling in Nairobi, Kenya
Kenneth Mubea1,2, Gunter Menz2,3
1Institute of Geomatics, GIS and Remote Sensing, Dedan Kimathi University of Technology, Nyeri, Kenya
2Remote Sensing Research Group (RSRG), University of Bonn, Bonn, Germany
3Centre for Remote Sensing of Land Surfaces (ZFL), University of Bonn, Bonn, Germany
Email: kpwmubea@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 September 2014; revised: 20 October 2014; accepted: 14 November 2014
ABSTRACT
Urban land-use modeling has gained increased attention as a research topic over the last decade. This has been attributed to advances in remote sensing and computing technology that now can process several models simultaneously at regional and local levels. In this research we implemented a cellular automata (CA) urban growth model (UGM) integrated in the XULU modeling frame-work (eXtendable Unified Land Use Modeling Platform). We used multi-temporal Landsat satellite image sets for 1986, 2000 and 2010 to map urban land-use in Nairobi. We also tested the spatial effects of varying model coefficients. This approach improved model performance and aided in understanding the particular urban land-use system dynamics operating in our Nairobi study area. The UGM was calibrated for Nairobi and predicted development was derived for the city for the year 2030 when Kenya plans to attain Vision 2030. Observed land-use changes in urban areas were compared to the results of UGM modeling for the year 2010. The results indicate that varying the UGM model coefficients simulates urban growth in different directions and magnitudes. This approach is useful to planners and policy makers because the model outputs can identify specific areas within the urban complex which will require infrastructure and amenities in order to realize sustainable development.
Keywords:
Urban Growth Model, Cellular Automata, XULU, Model Coefficients, Prediction, Sustainable Development

1. Introduction
Urban modeling studies are currently considered as an essential component for numerous complex environmental analyses [1] . These studies play a vital role in sustainable planning and are crucial for planning future urban development. Over the last few decades, cities in sub-Saharan Africa have experienced quite rapid growth rates; Nairobi grew at a rate of growth of 4.9 per cent between 1990 and 2006 [2] .
These high growth rates have been driven principally by large rural/urban migration into African cities as people search for employment and better living standards. This has led to pressures on existing urban infrastructure and amenities [3] . Problems linked to sustainable urban development in African cities are manifold and complex and solutions require an integrated approach. To be effective, such an integrated urban planning approach must allow planners to recognize and anticipate urban dynamics and their consequences [4] .
Modeling is one of the methods in the portfolio of tools and techniques available to characterize the dynamics of the land-use system [5] . Von Neumann [6] was one of the early pioneers of cellular automata (CA) and Tobler [7] first applied CA in geography. Models based on CA have evolved over the last decades in simulating urban development growth and patterns [8] . CA models have been used successfully in simulating dynamic spatial interactions by incorporating biophysical and socio-economic land-use change variables [9] -[11] . CA have shown potential in representing and simulating the complexity of the underlying processes involved in urban growth and land-use change, and have provided an additional level of knowledge and understanding of spatial and temporal change [12]
In this study, we implemented a XULU-based Urban Growth Model (UGM) for Nairobi. Reference [13] developed this UGM and first applied it in the German federal state of North-Rhine Westphalia. UGM is based on the modeling algorithm of the SLEUTH model [14] which uses the concept of cellular automata. For our analysis of Nairobi, calibration of UGM was based on the five model parameters described in the SLEUTH urban growth model [15] [16] . Model calibration was performed using land-use datasets for 1986 and 2010.
Little attention has been paid to the spatial effects of systematically varying each UGM parameter when implementing the model. This research is one of the first attempts to address this issue, and, following successful model calibration, we focused on the spatial effects of varying model parameters. Our objective was to systematically analyze and document the contribution of each model parameter in simulating urban growth. Urban land-use data for Nairobi were derived from annual Landsat image data acquired in 1986, 2000 and 2010. Model parameters were modified and tested in 31 separate simulations. Results reveal significant spatial effects in simulated urban land-use patterns between 1986 and 2010. The model was used to predict future urban land-use development in the year 2030. UGM was used successfully to study land use change and provide predictions of future urban land-use trends in Nairobi as Kenya accomplishes Vision 2030, the nation’s ambitious economic and social development program [17] .
2. The Study Area
Nairobi, the capital city of Kenya, extends between latitudes 1˚09' and 1˚28'South, and longitude 36˚04' and 37˚10'East. The city covers an area of 696 km2 and lies at an average altitude of 1700 meters above sea level (Figure 1). Nairobi uses the WGS 84 Universal Transverse Mercator (UTM) 37 South map projection. Within its administrative borders the city includes urban, agriculture, and rangeland land-uses as well as open/transitional areas, and remnants of evergreen tropical forests. Nairobi has a high annual population growth rate compared to other cities in Africa. From a population of 310,000 in 1960, the population reached 510,000 in 1970 (Republic of Kenya, 1970), 828,000 in 1979 [18] , 1,321,000 in 1989 [19] , 2,137,000 in 1999 [20] and 3,138,369 in 2009 [21] . The projected population in the year 2020 will be almost six million [22] . 75% of the city’s population lives in informal settlements [22] .
3. Modeling Nairobi’s Urban Growth
Our approach to urban growth modeling of Nairobi utilized information derived from multi-temporal Landsat satellite data in combination with additional datasets of slope, roads and an exclusion layer. Figure 2 illustrates the data processing flow developed for this urban growth model. Reference [23] developed XULU as a modeling framework that enables model integration and implementation using requisite functions of data storage, input/output methods, model runs, editing and visualization. The first use of XULU was to compute predicted future land-uses under varying change scenarios with their specific boundary conditions for a watershed in Benin [24] .
UGM has been implemented in the XULU modeling platform as a modification of the SLEUTH approach
Figure 1. Administrative boundary of Nairobi city (Source: False colour composite using bands 4, 3, 2, Landsat 2010).
Figure 2. Flowchart for urban growth modeling.
[11] [13] . UGM requires four spatial input parameters: urban land-use, transportation, slope and exclusion. The exclusion layer identifies those areas within the study site that cannot be changed (e.g. water bodies or protected areas) or areas which, if not excluded, are to a certain degree resistant to urbanization. The transportation layer represents the road network in a research area. While SLEUTH needs at least four urban land-use data sets to calculate a set of calibration coefficients [16] , the modified UGM in XULU only needs a map for the starting year of the calibration phase and a reference map at the end year. The simulated urban area of the end year is compared to the reference map using a Multiple Resolution Validation (MRV) procedure as described in Reference [25] .
Calibration is the most important step in any modeling application [15] . In the calibration phase of UGM a “brute-force” method is used to determine five calibration parameters. These parameters control the transition rules that are implemented in the model and include: Dispersion, Breed, Spread, Slope Resistance, and Road Gravity. Dispersion controls the number of image pixels that are randomly selected for possible urbanization and determines the extent of their outward distribution. Breed refers to the probability that a newly generated settlement initiates its own growth. Spread controls the extent to which existing settlements radiate. Slope resistance characterizes the likelihood of growth on steep slopes. Road gravity influences the creation of new centers along roads. Urban growth can be classified in UGM as: 1) spontaneous new growth; 2) new urban center establishment or spreading urban center growth; 3) edge growth; and, 4) road influenced growth [26] . Table 1 shows a summary of urban growth types simulated by our UGM as well as the contributing model parameters [26] .
UGM conducts simulation based on Cellular Automata (CA). CA is a discrete dynamic system in which space is divided into regular spatial cells, and time progresses in discrete steps [27] . Each cell in the system is characterized by one of a finite number of states. The state of every cell is updated at each discrete time-step according to a set of local rules and the state of a cell at a given time depends on its own state and the states of its neighbors at the previous time step [28] .
Following successful calibration of our Nairobi UGM, model parameters were modified in order to determine the spatial effects of each parameter combination. Each model parameter value ranges between 0 and 100 and thus indicates the respective contribution of each parameter in simulating urban growth. The “goodness of fit” of a set of parameters in a model is determined by a set of spatial metrics, each describing in a discrete way how accurately a set of parameters can replicate real-world historical patterns [12] . Several studies have examined the modification of existing urban land-use models so as to localize the models and identify optimal model parameters for each application [9] . Reference [29] examined SLEUTH model parameters for different counties and cities under Project Gigalopolis. Reference [30] explored sensitivity analysis for cellular automata modelling by varying neighbourhood size and type. Reference [31] performed a sensitivity analysis of the parameters within a logistic regression CA model and their influence on predicted urban gowth for metropolitan areas in China.
Model parameters are highly auto-correlated, making it difficult to understand each growth cycle in the evolution of an urban environment. We can observe only the reproduction of the overall urban complexity [30] . To better understand the role and importance of each UGM parameter, we conducted a series of urban growth simulations. In each simulation, each model parameter was modified individually by a value of +1 from optimal calibration values. We compared the resulting simulated urban maps with the predicted 2010 map using Kappa (K) statistics from the Map Comparison Kit (MCK) software [31] . MCK offers a combination of standard cell by cell map comparison (the K statistic and newly derived variants) as well as recent developments in fuzzy-set map comparison (K fuzzy) [31] .
4. Analysis
4.1. Data
Cloud-free Landsat satellite imagery for 1986, 2000 and 2010 were used to derive the land-use data layer required for the UGM. The city of Nairobi is entirely enclosed within Landsat TM path 168, row 61. The Landsat data sets used included TM, and ETM+ images in WGS-84 Universal Transverse Mercator (UTM), 37-South projection. Reference data were developed for each of the separate years and then randomly partitioned for classifier training and accuracy assessment. Ground truth data included a topographic map which was used as locational reference data for the 1986 and 2000 classifications while GPS points served as reference data for the 2010 classification. Road network data for Nairobi was obtained from Nairobi City Council and included all of the roads within the city. An exclusion layer was obtained from Survey of Kenya and included government buildings and property as well as other land areas designated as reserved.
Table 1. Summary of growth types simulated by the UGM model.
4.2. Land-Use Change Analysis
Land-use classification of Nairobi included six land-use classes: urban, forest, agriculture, open/transition areas, water and rangeland. Urban land-use included built-up areas within the research area. Forest included evergreen forest as well as high density mixed forests consisting of trees and little or no under-storey vegetation. Open/ transitional areas included bare land, exposed areas, quarries and transitional areas. Water included rivers and reservoirs. The sewage treatment plant in Ruai was also included in the water class. Rangeland included bush land and ground layer covered by grass and sparsely disturbed scrub species. The design of the classification scheme involved consideration of factors such as the major land-use groups within the research area, disparities in spatial resolution of the remote sensor data, and the need to consistently discriminate land-use classes irrespective of seasonal disparities [32] .
Image pre-processing steps for the optical datasets included radiometric and geometric correction. GPS points were used for image to map registration. Combinations of the image reflectance spectral bands (i.e., stacked vectors) were used for classification of the 1986, 2000 and 2010 images. Training sites representing the land-use classes of interest were collected using the Region of Interest tool in ENVI 4.8. Support vector machine (SVM) classification was applied to all the data sets and its performance assessed using error matrices. Recently, the SVM classification approach has been demonstrated as superior in comparison to maximum likelihood classifiers [33] .
Post-classification refinements were utilized to diminish classification errors as a result of the similarities in spectral signatures of certain classes. Independent samples of pixels for each class were randomly selected from each classification category to assess classification accuracies. Error matrices as cross-tabulations of mapped classes versus reference classes were compiled and used to assess classification accuracies [34] . Overall classification accuracy, user’s and producer’s accuracies, and the Kappa statistic were then derived from the error matrices.
4.3. Modeling
Inputs for UGM included land-use datasets (1986 and 2010), slope data, exclusion data and road data for Nairobi. Land-use data for 1986 were used as the base data for modeling while land-use data for 2010 were used as the reference grid. These land-use maps all satisfied the minimum accuracy requirement of 85% stipulated in the Anderson classification scheme [32] . Land-use data for the three dates were each reclassified to a binary map showing only urban and non-urban land-uses. Slope data was derived from the Digital Elevation Model (DEM) of Nairobi at 30 meters spatial resolution. Exclusion data was used to place constraints on urban growth and included areas within Nairobi where development is restricted, including government property and buildings, parks and reserved areas.
Road data included a complete road network for Nairobi, and for modeling purposes, the major roads within the city were assigned a weighting factor. The road layer included three weight values of 100, 50 and 25 [12] [16] . A weighting factor of 100 was assigned to class A roads (International trunk roads), a factor of 50 was assigned to class B and C roads (National Trunk Roads), and a value of 25 was assigned to local streets (Minor roads). The road classification in Kenya is explained in more detail in Reference [35] . Development within Nairobi was most likely to occur along the major roads. Modeling was done at 100 meters spatial resolution, and all datasets were resampled to this level.
Model calibration of UGM involved running the model using default values of 1, 50 and 100 for slope, breed, dispersion, road, and spread parameters. Model calibration was done iteratively in four sequences from coarse to fine calibration as the parameters were varied. The MRV method was used to achieve the optimal parameterization for the UGM during the calibration phase as well as for validation of the model results. The Multiple Resolution Validation (MRV) method was first used in a thorough comparison of land-use models in which the tests were conducted in seven laboratories with 13 applications, 9 different models and in 12 study areas [25] .
In order to explore spatial effects of our UGM, we conducted tests of parameter combinations and permutations according to the Equation (1). The value of runs for each combination was obtained where n is the number of parameters (in this case, five) and r is the parameters to be maintained constant. We obtained five sets of results for the first combination, ten sets for the second combination, ten sets for the third combination, five sets for the fourth combination, and one set for the fifth combination.
 (1)
(1)
In total we obtained 31 simulated urban growth maps. In order to evaluate the spatial effects within each map, we used the Map Comparison Kit (MCK) software [31] to generate  statistics using the predicted map of 2010. Reference [36] describes
statistics using the predicted map of 2010. Reference [36] describes 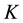 statistics and additional statistics within
statistics and additional statistics within 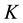 including Khisto and Klocation.
including Khisto and Klocation.
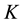 is a measure of similarity between two maps based on a contingency table [31] [37] .
is a measure of similarity between two maps based on a contingency table [31] [37] . 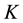 is defined according to Equation (2) where
is defined according to Equation (2) where  is the proportion of cases in agreement (i.e., correctly allocated) and
is the proportion of cases in agreement (i.e., correctly allocated) and 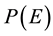 is the proportion of agreement that is expected by chance:
is the proportion of agreement that is expected by chance:
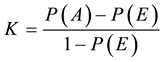 (2)
(2)
Klocation is a measure of the similarity of the spatial allocation of categories of the two compared maps [25] . 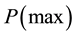 gives the maximal similarity that can be found based upon the total number of cells allocated to each category. Klocation is calculated according to Equation (3):
gives the maximal similarity that can be found based upon the total number of cells allocated to each category. Klocation is calculated according to Equation (3):
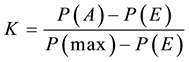 (3)
(3)
Khisto is a measure of the quantitative similarity of the two compared map [36] . Thus Khisto makes it possible to express  as a combination of similarity in quantity and location as shown in Equation (4):
as a combination of similarity in quantity and location as shown in Equation (4):
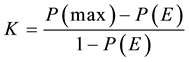 (4)
(4)
5. Results and Discussion
A land-use summary for Nairobi was performed and results tabulated in Table 2 and Figure 3. Land-use maps for Nairobi are illustrated in Figures 4-6. The urban/built-up areas increased from 35.16 km2 in 1986 to 52.50 km2 in 2000 and 79.38 km2 in 2010. Forest increased from 62.87 km2 in 1986 to 71.14 km2 in 2000 but decreased to 66.86 km2 in 2010. Areas where forest decreased were classified as agriculture or urban. Agriculture increased from 144.72 km2 in 1986 to 152.53 km2 in 2000 but decreased to 148.21 km2 in 2010. Typical agriculture land-use included small scale gardens and peri-urban agriculture. These areas were converted to urban land-use with the construction of residential and commercial buildings necessary for the increased urban population in Nairobi. Open/Transition areas increased from 99.54 km2 in 1986 to 146.94 km2 in 2000 but decreased to
Table 2. Land-use summary and error estimates for Nairobi.
Figure 3. Land-use estimates for Nairobi.
Figure 4. Land-use map of Nairobi derived from Landsat TM 1986.
117.94 km2 in 2010. Rangeland decreased from 361.11 km2 in 1986 to 261.74 km2 in 2000 and 257.61 km2 in 2010. Water increased from 9.60 km2 in 1986 to 11.15 km2 in 2000 and increased further to 26.00 km2 in 2010.
Modeling of Nairobi utilized as inputs urban extents extracted from classified land-use maps for 1986 and 2010. Other layers used included slope, areas excluded from development and the Nairobi road network. A nearest neighbor technique was used to resample all of the datasets to a spatial resolution of 100 meters. Calibration was performed using the 2010 land-use map as a reference grid. The best model parameters for UGM were also evaluated based on the weighted average calculated with the MRV using 2010 land-use as a reference grid.
Figure 7 shows the best model coefficients obtained following successful calibration of UGM at 100 meter spatial resolution. These coefficient values are: slope = 52, spread = 27, dispersion = 1, breed = 52, road = 2. These coefficients were obtained at a weighted value of 0.95. We therefore conclude that the UGM calibration produced an agreement of approximately 95% for the built-up/non-built-up categories between the 2010 reference map and the 2010 map fitted with the model.
In order for an urban growth model to be of use to policy makers and urban planners, simulation of urban growth must be performed after calibration. To demonstrate this capability, we used UGM to predict Nairobi land-use for the year 2030. We started by using 2010 land-use as reference data during the UGM calibration, and proceeded under the assumption that current urban planning policies would remain constant. The expansion of urban land-use (built-up areas) was modeled with the UGM using the identical model parameters obtained in the 1986-2010 calibration (Figure 7) at 100 meters spatial resolution.
Simulated urban land-use estimates for Nairobi in 2030 were achieved using the calibrated UGM. This exercise predicts that urban land-use in Nairobi will increase from 73.14 km2 in 2010 to118.35 km2 in 2030. The map of simulated urban land-use for Nairobi in 2030 is shown in Figure 8. The prediction of new settlements or built-up areas in Nairobi was derived at a weighted value of 0.95. The model predicts that new urban growth in the city is most likely to be influenced by breed and slope parameters; both showing values of 52. The spread parameter is next in importance, at a value of 27. The road and dispersion parameters are shown to be the least likely factors in new urban growth. These results suggest that new areas will be developed in proximity to roads, principally for residential and commercial uses. Such growth could result from the high rural to urban migration into Nairobi, as new residents arrive in the city in search of employment, social amenities and economic opportunity.
Figure 5. Land-use map of Nairobi derived from Landsat ETM 2000.
Figure 6. Land-use map of Nairobi derived from Landsat ETM+ 2010.
Figure 7. Best model parameters for Nairobi UGM.
Figure 8. Simulated urban growth for Nairobi, 2010-2030.
In order to analyze the influence of each individual parameter upon the UGM, 2010-2030 urban growth was simulated varying each of the best model parameters by a value of +1. The best model parameters obtained using UGM yielded a simulated urban growth of 73.14 km2. A total of 31 simulations were conducted; results of the five combination sets are shown in Tables 3-7. K statistics were used for map comparisons.
Table 3 summarizes the 1st combination. In this combination, the four best parameters were each varied by a value of +1, with one parameter remaining constant (shown in bold in Table 3). The simulated urban growth figures all exceed the 73.14 km2 figure obtained using the best model parameters (Figure 7). The highest spatial effect is realized in Set 5, where the slope value is held constant while the other values were varied. In Set 5, urban growth = 79.99 km2, with the lowest resultant Khisto value of 0.950. Again, the Khisto measure makes it possible to express K as a combination of similarity in quantity and location. The lowest spatial effect (75.77 km2) with the highest Khisto value (0.980) was observed in Set 4, where the road value was held constant while the others were varied.
Table 4 shows the 2nd combination in which the three best parameters were varied by +1 and two parameters (shown in bold in the Table 4) remained constant. Again, simulated urban growth values are uniformly greater than the 73.14 km2 figure predicted using the optimal model parameters (Figure 7). Set 8 yielded a value of 73.31 km2 with a high Khisto value of 0.999. This value is quite close to the simulated urban growth value of 73.14 km2, indicating a minimum of spatial effect in this model. The highest spatial effect (79.14 km2) and lowest Khisto value (0.954) was observed in Set 14, in which the slope and breed parameters were held constant while the others were varied.
Table 5 summarizes the 3rd combination, where the two best parameters were varied by +1 and the other three parameters remained constant (again shown in bold). Again, the simulated urban growth values are greater than the 73.14 km2 figure obtained using best model parameters as shown in Figure 7. Set 19 yielded a simulated urban growth value of 73.16 km2 with a high Khisto value of 0.996. This simulated urban growth value is very close to the figure of 73.14 km2 produced by the original calibrated UGM model. Thus, varying two model parameters Dispersion (at 2) and Slope (at 53)―in Set 19 yields a good fit curve for urban growth modeling along with the least spatial effect. In contrast, Set 20 yielded the highest spatial effect (77.32 km2) with a low Khisto value (0.985). These figures result from varying Dispersion at 2 and Slope at 52 (rather than 53 as in Set 19).
Table 6 shows the 4th combination where the single best parameter was varied by +1 while keeping the other four parameters constant (shown in bold). The simulated urban growth values are greater than the value of 73.14 km2 obtained using best model parameters (Figure 7). Set 26 yielded a value of 73.18 km2 with the highest Khisto value of 1.000. The 73.18 km2 value was closest to the simulated urban growth value of 73.14 km2. Varying only the Slope parameter in set 26 yielded the least spatial effect. It is useful to compare these results with those produced in Set 30 in which only the Spread parameter was varied. Set 30 yielded the highest spatial effect; an indication of the sensitivity of our UGM in modeling urban growth.
Table 3. Model parameter variation in 1st combination for UGM of Nairobi.
Table 4. Model parameter variation in 2nd combination for UGM of Nairobi.
Table 7 shows the 5th combination under which all of the best parameters were varied by a value of +1. The simulated urban growth value produced by this combination was 77.29 km2 with a Khisto value of 0.969. This growth value significantly exceeds the 73.14 km2 figure yielded by using best model parameters. It is clear that varying all parameters affects our UGM significantly.
In this research we explored the spatial effects of varying the UGM model parameters and the results indicate the sensitivity of our UGM in urban growth modeling. Varying at least one model parameter while leaving the other parameters constant had a significant effect on the resulting simulated urban growth values. The highest spatial effect obtained was 79.99 km2 (Table 3) while the lowest value derived was 73.16 km2 (Table 5). The value of 79.99 km2 was obtained as the Slope parameter was held constant while the others were varied. The value of 73.16 km2 was obtained by holding Spread, Breed, and Road parameters constant while varying Dispersion and Slope. In addition, examining Table 6 shows that the value of 73.18 km2 was the second lowest
Table 5. Model parameter variation in 3rd combination for UGM of Nairobi.
Table 6. Model parameter variation in 4th combination for UGM of Nairobi.
Table 7. Model parameter variation in 5th combination for UGM of Nairobi.
value obtained for spatial effect. This figure was obtained by varying the Slope parameter and holding the other parameters constant.
Analysis of the lower spatial effect values (73.16 km2 from Table 5 and 73.18 km2 from Table 6), shows that these results are produced by holding Spread, Breed and Road parameters constant. This suggests that these three model parameters are closely correlated in the production of similar amounts of urban growth cells. Model sets yielding a low spatial effect and those with a high spatial effect are shown in Table 8 and Table 9.
From Tables 4-6 it is clear that maintaining constant values for Dispersion and Slope at a minimum yielded high spatial effects (78.23 km2, 76.93 km2 and 76.48 km2). As the value of the Road parameter was increased we observed in all simulations increasing urbanization of more accessible areas. This connection to the road net work is evident with equal growth rates (due to the values of the other parameters), an effect observed by Reference [38] .
Table 9 shows the urban growth simulations for the 31 Sets. Again, the simulated urban growth value of 73.14 km2 was produced by UGM using the best model parameters (Figure 7). Table 9 shows that Set 19 produced an urban growth value of 73.16 km2, the closest to that produced by the UGM (also in Table 5).
Figure 10 shows the K and Klocation values for the 31 simulations. In Set 24 model parameters of Dispersion, Road and Slope were held constant. Set 24 had the highest K value of 0.764 indicating the high spatial effect associated with this Set (75.19 km2). In set 31 all model parameters were varied and Set 31yielded the lowest K value (0.736) along with a high spatial effect of 77.02 km2. High K values indicate low similarity between the maps and therefore a high spatial effect. In Set 10 two model parameters―Dispersion and Breed―were kept constant. Set 10 generated the highest Klocation value of 0.783; this is indicative of the high spatial effect, measured at 78.01 km2. In set 8 where the two parameters of Spread and Road were kept constant, both a low K value and a low spatial effect (73.31 km2) were produced. High K and Klocation values describe low similarity between the maps and indicate high spatial effects.
Additionally, Figure 10 shows that low K and Klocation values were observed in Sets 8 and 9; 0.739 in Set 8 and 0.740 in Set 9, with the lowest Klocation value being observed in Set 8. In these two Sets only the Spread model parameter was held constant. Set 31 yielded the lowest K value at 0.736.
Table 8. Model parameter sets with low spatial effect for UGM of Nairobi.
Table 9. Model parameter sets with high spatial effect for UGM of Nairobi.
Figure 11 shows the Khisto values for the 31 simulations. The highest value of Khisto (1.000) was obtained in both Set 19 and in Set 26. In Set 19 three model parameters (Spread, Breed, and Road) were kept constant, In Set 26 four parameters (Spread, Dispersion, Breed and Road) were held constant. This high Khisto value indicates the lowest spatial effect. In set 5, where a single parameter (Slope) was kept constant, the lowest Khisto value of 0.950 was produced, indicating the highest spatial effect observed at 79.99 km2. High Khisto values indicate a high degree of similarity between the maps in terms of quantity and location of predicted urban growth and indicate the lowest spatial effect.
Table 8 presents the set of parameters that yielded the minimum urban growth levels and indicate low spatial effect. The lowest spatial effect of 73.16 km2 is indicated by the highest Khisto value of 1.000. It is clear that maintaining the values of the Spread, Breed and Road parameters leads to a low spatial effect and indicates that these three model parameters are highly correlated. The growth types predicted were: new spreading growth as a result of Breed; edge growth as a consequence of Spread; and road-influenced growth as a result of the Road parameter.
Table 9 presents the set of parameters that produced the maximum urban growth levels. Maintaining only the Slope parameter and increasing the values of the other four parameters resulted in a high spatial effect at 79.99 km2 along with the lowest Khisto value of 0.950. However, holding the Dispersion, Breed and Road parameters constant while varying the other two parameters produced a low spatial effect (76.48 km2) with a high Khisto value of 0.975. This suggests that the Dispersion, Breed and Road model parameters are moderately correlated, but less so than the Spread, Breed and Road model parameters (see Table 8).
Figure 9. Spatial effects of 31 UGM simulations.
Figure 10. K and Klocation values for urban growth simulation.
Maintaining Spread, Breed and Slope constant resulted in the lowest spatial effect value of 73.16 km2 (Table 8) with the highest Khisto value of 1.000, as illustrated in Figure 12. The highest spatial effect of 79.99 km2 (Table 9) with the lowest Khisto value of 0.950 is mapped in Figure 13. Figure 12 and Figure 13 both include the 2010 simulated urban growth map and the simulated spatial effect map. Additionally, statistics from Figure 12 and Figure 13 including the four map categories are shown in Table 10.
From Table 10 it can be seen that for the lowest spatial effect case identical values are present for Categories 3 and 4. In the highest spatial effect case the values for Categories 3 and 4 differ significantly; 14.21 km2 for Category 3, and 21.06 km2 for Category 4. The values for Categories 1 and 2 are quite similar. Examining the spatial effect as shown in Category 4, reveals a difference of 4.68 km2 (16.38 km2 and 21.06 km2), confirming the sensitivity of our UGM.
These results can help regional and urban planners to understand the implications of varying the parameters in the Urban Growth Model. This can allow planners to simulate differing future urban growth scenarios by incorporating varying combinations of model parameters. Higher spatial effects in model outputs translate to simulations with increasing urban sprawl. Lower spatial effects translate to less urban sprawl simulation. This information can be effective in the design of “smart” cities, which is a vital research agenda in modern urban planning.
Figure 11. Khisto values for urban growth simulation.
Figure 12. Lowest spatial effect based parameters values obtained from set 19 (see Table 8).
Figure 13. Highest spatial effect based parameters values obtained from set 5 (see Table 9).
Table 10. Statistics of spatial effect maps.
6. Conclusions
Nairobi, Kenya’s capital, was used as an example of a rapidly expanding African city to analyze the spatial effects of varying urban growth parameters in urban land-use modeling. UGM uses cellular automata in urban growth modeling and simulation. We explored a number of different combinations of UGM parameters and their spatial effects. Each model parameter influences urban growth independently. The question of which model combinations produce least or highest spatial effect was the focus of this research.
The Spread, Breed and Road model parameters were observed to be highly correlated. In addition, Kappa statistics were used to compare simulation maps. The lowest spatial effect was achieved by holding constant the Spread, Breed and Road model parameters while varying the other parameters. This also translated to the highest value of Khisto. The highest spatial effect was observed by keeping the Slope parameter constant while varying the other four parameters. This also translated to the lowest Khisto value. High Khisto values indicate high quantity and location similarity between the maps and are indicative of the lowest spatial effect.
By the year 2030, the nation of Kenya plans to achieve Vision 2030, an ambitious economic and social development program. Effective urban and regional planning is a critical component of the Vision 2030 program. Information on the spatial effects of the UGM described in this study can assist in identification of optimal scenarios of future urban growth. It is possible to accurately identify areas that are likely to experience spontaneous growth, edge growth, road-influenced growth or growth arising from new spreading centers. By simulating various urban growth scenarios, policy makers can analyze the effects of establishing new housing and road infrastructure in undeveloped areas rather than in existing settlements. The UGM can provide an accurate and useful guide to the growth of Nairobi, as well as identify and illustrate areas in which expansion can best take place. The UGM can even serve as a master planning tool. Cellular automata modeling is an effective approach for regional modeling of African cities such as Nairobi, and can be adapted to provide effective opportunities to study other African cities using UGM.
Acknowledgements
The authors express their gratitude to the initiators of XULU and especially M. Schmitz, H. P. Thamm, Th. Bode and A. B. Cremers. Additionally, the authors are grateful to German Academic Exchange Service (DAAD) and National Council for Science and Technology (NCST in Nairobi, Kenya) for providing the stipend to facilitate this research. Moreover, the authors acknowledge the contribution of Joseph Scepan (Oregon, USA) as well as other, anonymous reviewers for their useful comments.
References
- Triantakonstantis, D. and Mountrakis, G. (2012) Urban Growth Prediction: A Review of Computational Models and Human Perceptions. Journal of Geographic Information System, 4, 555-587. http://dx.doi.org/10.4236/jgis.2012.46060
- UN-HABITAT (2010) State of the World Cities 2010/2011. Bridging the Urban Divide. http://sustainabledevelopment.un.org/content/documents/11143016_alt.pdf
- Mundia, C.N. and Aniya, M. (2007) Modeling Urban Growth of Nairobi City Using Cellular Automata and Geographical Information Systems. Geographical Review of Japan, 80, 777-788. http://dx.doi.org/10.4157/grj.80.777
- Mundia, C.N., Aniya, M. and Murayama, Y. (2010) Remote Sensing and GIS Modeling of Spatial Processes of Urban Growth in an African City. A Case Study of Nairobi. In: Mundia, C.N., Kamusoko, C. and Murayama, Y., Eds., Recent Advances in GIS and Remote Sensing Analysis in Sub-Sahara Africa, Nova Science Publishers, New York.
- Verburg, P. (2006) Simulating Feedbacks in Land Use and Land Cover Change Models. Landscape Ecology, 21, 1171- 1183. http://dx.doi.org/10.1007/s10980-006-0029-4
- Von Neumann, J. (Burks, A.W., Ed.) (1966) Theory of Self-Reproducing Automata Theory of Self-Reproducing Automata. University of Illinois Press, Champaign.
- Tobler, W. (1979) Cellular Geography. In: Gale, S. and Olsson, G., Eds., Philosophy in Geography, Reidel, Dortrecht, 379-386.
- Silva, E. and Clarke, K.C. (2002) Calibration of the SLEUTH Urban Growth Model for Lisbon and Porto, Portugal. Computers, Environment and Urban Systems, 26, 525-552. http://dx.doi.org/10.1016/S0198-9715(01)00014-X
- Jantz, A.J., Goetz, S.J., Donato, D. and Claggett, P. (2010) Designing and Implementing a Regional Urban Modeling System Using the SLEUTH Cellular Urban Model. Computers, Environment and Urban Systems, 34, 1-16. http://dx.doi.org/10.1016/j.compenvurbsys.2009.08.003
- Fuglsang, M., Münier, B. and Hansen, H.S. (2013) Modelling Land-Use Effects of Future Urbanization Using Cellular Automata: An Eastern Danish Case. Environmental Modelling & Software, 50, 1-11. http://dx.doi.org/10.1016/j.envsoft.2013.08.003
- Mubea, K., Goetzke, R. and Menz, G. (2013) Simulating Urban Growth in Nakuru (Kenya) Using Java-Based Modelling Platform XULU. UKSim-AMSS 7th European Modelling Symposium, Manchester, 20-22 November 2013, 103- 108. http://dx.doi.org/10.1109/EMS.2013.18
- Dietzel, C. and Clarke, K.C. (2007) Toward Optimal Calibration of the SLEUTH Land Use Change Model. Transactions in GIS, 11, 29-45. http://dx.doi.org/10.1111/j.1467-9671.2007.01031.x
- Goetzke, R. and Judex, M. (2011) Simulation of Urban Land-Use Change in North Rhine-Westphalia (Germany) with the Java-Based Modelling Plat-Form Xulu. In: Mandl, P. and Koch, A., Eds., Modelling and Simulating Urban Processes, LIT-Verlag, Munster, 99-116.
- Clarke, K., Hoppen, S. and Gaydos, L. (1997) A Self-Modifying Cellular Automaton Model of Historical Urbanization in the San Francisco Bay Area. Environment and Planning B: Planning and Design, 24, 247-261. http://dx.doi.org/10.1068/b240247
- Clarke, K., Hoppen, S. and Gaydos, L. (1996) Methods and Techniques for Rigorous Calibration of Cellular Automaton Model of Urban Growth. 3rd International Conference/Workshop on Integrating GIS and Environmental Modeling, Santa Fe, 21-25 January 1996, Session 7. http://www.ncgia.ucsb.edu/conf/SANTA_FE_CD-ROM/program.html
- Silva, E. and Clarke, K.C. (2002) Calibration of the SLEUTH Urban Growth Model for Lisbon and Porto, Portugal. Computers, Environment and Urban Systems, 26, 525-552. http://dx.doi.org/10.1016/S0198-9715(01)00014-X
- Government of Kenya (2007) Kenya Vision 2030. http://www.theredddesk.org/sites/default/files/vision_2030_brochure__july_2007.pdf
- Republic of Kenya (1981) Kenya Population Census 1979. Government Printer, Nairobi.
- Republic of Kenya (1994) Kenya Population Census 1989. Government Printer, Nairobi.
- Republic of Kenya (2000) Economic Survey 2000. Government Printer, Nairobi.
- Republic of Kenya (2010) Economic Survey 2010. Government Printer, Nairobi.
- UN-HABITAT (2005) Regional Urban Sector Profile Study. UN-HABITAT, Nairobi.
- Schmitz, M., Bode, T., Thamm, H.P. and Cremers, A.B. (2007) XULU―A Generic JAVA-Based Platform to Simulate Land Use and Land Cover Change. In: Oxley, L. and Kulasiri, D., Eds., MODSIM 2007 International Congress on Modelling and Simulation, Modelling and Simulation Society of Australia and New Zealand, 2645-2649.
- Menz, G., Judex, M., Orekan, V., Kuhn, A., Heldmann, M. and Thamm, H.P. (2010) Land Use and Land Cover Modeling in Central Benin. In: Spezh, P., Christoph, M. and Dieckkrüger, B., Eds., Impacts of Global Change on the Hydrological Cycle in West and Northwest Africa, Springer, Heidelberg, 70-73.
- Pontius Jr., R.G., Huffaker, D. and Denman, K. (2004) Useful Techniques of Validation for Spatially Explicit Land- Change Models. Ecological Modelling, 179, 445-461. http://dx.doi.org/10.1016/j.ecolmodel.2004.05.010
- Jantz, C.A., Goetz, S.J. and Shelley, M.K. (2004) Using the SLEUTH Urban Growth Model to Simulate the Impacts of Future Policy Scenarios on Urban Land Use in the Baltimore-Washington Metropolitan Area. Environment and Planning B: Planning and Design, 31, 251-271. http://dx.doi.org/10.1068/b2983
- Liu, Y. (2008) Modelling Urban Development with Geographical Information Systems and Cellular Automata. CRC Press, Boca Raton.
- Wolfram, S. (1994) Cellular Automata. In: Wesley, A., Wolfram, S. and Reading, M.A., Eds., Cellular Automata and Complexity: Collected Papers, Westview Press, Boulder, 411-436.
- Caglioni, M., Pelizzoni, M. and Rabino, G.A. (2006) Urban Sprawl: A Case Study for Project Gigalopolis Using SLEUTH Model. In: El Yacoubi, S., Chopard, B. and Bandini, S., Eds., Cellular Automata, Springer Berlin Heidelberg, Heidelberg, 436-445. http://dx.doi.org/10.1007/11861201_51
- Kocabas, V. and Dragicevic, S. (2006) Assessing Cellular Automata Model Behaviour Using a Sensitivity Analysis Approach. Computers, Environment and Urban Systems, 30, 921-953. http://dx.doi.org/10.1016/j.compenvurbsys.2006.01.001
- Han, J., Cao, X. and Imura, H. (2009) Application of an Integrated System Dynamics and Cellular Automata Model for Urban Growth Assessment: A Case Study of Shanghai, China. Landscape and Urban Planning, 91, 133-141. http://dx.doi.org/10.1016/j.landurbplan.2008.12.002
- Visser, H. and de Nijs, T. (2006) The Map Comparison Kit. Environmental Modelling and Software, 21, 346-358. http://dx.doi.org/10.1016/j.envsoft.2004.11.013
- Anderson, J.R., Hardy, E.E., Roach, J.T. and Witmer, R.E. (1976) A Land Use and Land Cover Classification System for Use with Remote Sensor Data. Geological Survey, Washington DC.
- Mubea, K. and Menz, G. (2012) Monitoring Land-Use Change in Nakuru (Kenya) Using Multi-Sensor Satellite Data. Advances in Remote Sensing, 1, 74-84. http://dx.doi.org/10.4236/ars.2012.13008
- Congalton, R.G. and Green, K. (1999) Assessing the Accuracy of Remotely Sensed Data: Principles and Practices. Lewis Publishers, Florida.
- Wasike, W.S. (2001) Road Infrastructure Policies in Kenya: Historical Trends and Current Challenges. KIPPRA Working Paper No. 1. The Kenya Institute for Public Policy Research and Analysis (KIPPRA), Infrastructure and Economic Services Division, Nairobi, 1-42.
- Hagen, A. (2002) Multi-Method Assessment of Map Similarity. In: Ruiz, M., Gould, M. and Ramon, J., Eds., Proceedings of the 5th AGILE Conference on Geographic Information Science, European Commission, Palma, 171-182.
- Foody, G.M. (2004) Thematic Map Comparison: Evaluating the Statistical Significance of Differences in Classification Accuracy. Photogrammetric Engineering and Remote Sensing, 70, 627-633. http://dx.doi.org/10.14358/PERS.70.5.627















