Journal of Geographic Information System
Vol. 4 No. 1 (2012) , Article ID: 17061 , 9 pages DOI:10.4236/jgis.2012.41006
The Rough Method for Spatial Data Subzone Similarity Measurement
School of Mathematics and Information, Guangxi University, Nanning, China
Email: gisliaowh@163.com
Received September 7, 2011; revised November 2, 2011; accepted November 28, 2011
Keywords: Subzone; Rough Sets; Neighborhood Rough Sets; Similarity Measurement
ABSTRACT
There are two methods for GIS similarity measurement problem, one is cross-coefficient for GIS attribute similarity measurement, and the other is spatial autocorrelation that is based on spatial location. These methods can not calculate subzone similarity problem based on universal background. The rough measurement based on membership function solved this problem well. In this paper, we used rough sets to measure the similarity of GIS subzone discrete data, and used neighborhood rough sets to calculate continuous data’s upper and lower approximation. We used neighborhood particle to calculate membership function of continuous attribute, then to solve continuous attribute’s subzone similarity measurement problem.
1. Introduction
GIS entity has some spatial relevance in real world. Tober [1] proposed the famous geography first law “The spatial entities are always interrelated, especially, it have more obvious character for closed distance entities”. Cliff [2] put forward spatial autocorrelation concept from this established law, and the concept is the information for a spatial unit having similarity for it’s around units as summarized in Wang [3]. And the spatial autocorrelation has been widely used in many fields, such as regional economy, application ecology, scene analysis, preventive medicine and so on [4]. Anselin [5] found the spatial autocorrelation has two measurement index, that is global index and local index. Global index study the spatial mode for whole region, and it use a single value to reflect the region’s spatial autocorrelation degree. Local index calculate each unit degree of correlation from its neighbor unit for one attribute. And it has widely application domain as a similarity problem tool.
GIS subzone measurement is actually an uncertainty study problem. Li [6] found the uncertainty problem study works have attracted more and more attention by many study workers since entering the 21st century. There are many mathematic tools for study uncertainty problem, such as fuzzy sets, rough sets, quotient space etc. Rough sets have been widely used in GIS uncertainty study, Pawlak [7] introduced Rough sets theory and discussed in greater detail in Refs [8,9]. It is a technique for dealing with uncertainty and for identifying cause—effect relationships in databases as a form of data mining and database design. It is as summarized in R. Slowinski [10]. Slowinsk found it has also been used for improved information retrieval. Srinivasan [11] and Beaubouef [12,13] found it is also used in uncertainty management in relational databases. Theresa Beaubouef [14] used rough sets to describe the fuzziness, uncertainty, GIS topological relation, 9-intersection model, egg yolk model for GIS entity and GIS data reasoning. The Pawlak rough sets took all the study objects as universe, and used equivalence relation to divide the universe into some exclusive equivalence class, then took it as basic information partial in universe description. For discretionary concept in equivalence space, Hu [15] suggested that Pawlak rough sets took two equivalence class union sets: upper and lower approximation to approach it. But as an effective granular computing model, Pawlak rough sets are suit for dealing with nominal variable and discrete data that because it is based on classic equivalence class and equivalence relation. Then Xie [16] found the researcher took continuous numerical attribute into nominal variable and discrete data with discrete algorithms for rough sets method in processing data. Jensen [17] suggested this transformation inevitably brings the information loss. The compute result is largely rest with the discretization result. To solve this problem, Duboi [18], Hu [19], Yeung [20] et al. [21,22] introduced fuzzy rough sets, similarity relation rough sets model and neighborhood rough sets. Lin [23] put forward neighborhood rough sets model concept, this model took the space neighbor point to granulating universe, and took neighbor as basic information particle, then Lin [23] took it to describe others concepts in approximation space. The math pathfinders have done many study works about rough sets similarity. Wu [24] given three forms of the differences of rough fuzzy set, and discussed their basic properties, they think that the number of conditions for the difference degree of rough fuzzy set should have must be satisfied. Guan [25] defined the concept of rough similarity degree between two rough sets by using fuzzy sets induced by rough sets, and discussed its properties, and compared four kinds of rough similarity degree in the approximation space.
So it has many studies about similarity measurement for discrete value and continuous value in mathematics. There are two Similarity measurement correlations methods in GIS, one is cross-coefficient, and the other is spatial autocorrelation that based on spatial location. These two methods can not measure similarity of GIS subzone. This paper use rough sets measurement method to measure two subzone’s similarity problem, simultaneously study the subzone’s similarity based on one universe set.
2. Spatial Autocorrelation and Cross-Coefficient
2.1. Global Spatial Autocorrelation
Global spatial autocorrelation is an attribute value description of whole region spatial character. And it estimated global spatial autocorrelation statistic for global Moran’s I and global Geary’s C, to analyze total region spatial correlation and spatial discrepancy. And global Moran’s I is used commonly, it is defined as follows:
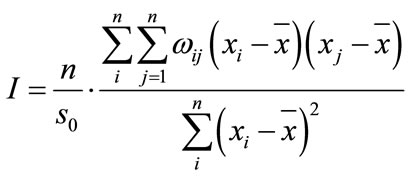 (1)
(1)
where xi is the observed value for observed spatial cell,
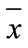 is the average value for each observed value, S0 is the sum of all element spatial weight matrix (W), and it can obtained from the follows formula:
is the average value for each observed value, S0 is the sum of all element spatial weight matrix (W), and it can obtained from the follows formula:
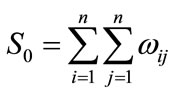 (2)
(2)
 is the spatial weighting matrix, and the value of
is the spatial weighting matrix, and the value of  can obtain from follows formula:
can obtain from follows formula:
 (3)
(3)
where n is the number for spatial cell. And if the i cell and the j cell are neighborhood, then  = 1, otherwise
= 1, otherwise 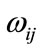 = 0. And one cell is neighborhood for itself, namely
= 0. And one cell is neighborhood for itself, namely 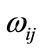 = 1. It can use Z test to statistic test its result after computing Moran’s I, it can obtain from follows formula (4):
= 1. It can use Z test to statistic test its result after computing Moran’s I, it can obtain from follows formula (4):
 (4)
(4)
It is frequently took Moran’s I as cross-coefficient, and the value of Moran’s I is between –1 and 1. In given level of significance, when Moran’s I is obviously positive, it indicates each observed value has positive correlation, and higher observed value is cluster to higher observed value, lower observed value is cluster to lower observed value, it presents higher to higher cluster or lower to lower cluster. when Moran’s I is obviously negative, it indicates each observed value has negative correlation, and higher observed value is cluster to lower observed value, it presents dispersed pattern. When the Moran’s I trends to 0, it express that it has no spatial autocorrelation, it is random patterns for spatial observed value.
Example 1 considering the example seen in Figure 1, there are nine polygons, the number ID from left to right, top to down is {1, 2, 3, 9}. The label of each polygon in Figure 1 is the value of each polygon. We can see the value of each polygon is continuous spatial value. Then we can calculate the global Moran’s I value is 0.028508, Z value is 0.636673. So the distribution of Figure 1 is a dispersed and random spatial pattern.
9}. The label of each polygon in Figure 1 is the value of each polygon. We can see the value of each polygon is continuous spatial value. Then we can calculate the global Moran’s I value is 0.028508, Z value is 0.636673. So the distribution of Figure 1 is a dispersed and random spatial pattern.
2.2. Local Spatial Autocorrelation
Global Moran’s I is an overall statistic index, and it only illustrated the average degree of region and adjacent region. Local spatial disparities may expand, when the
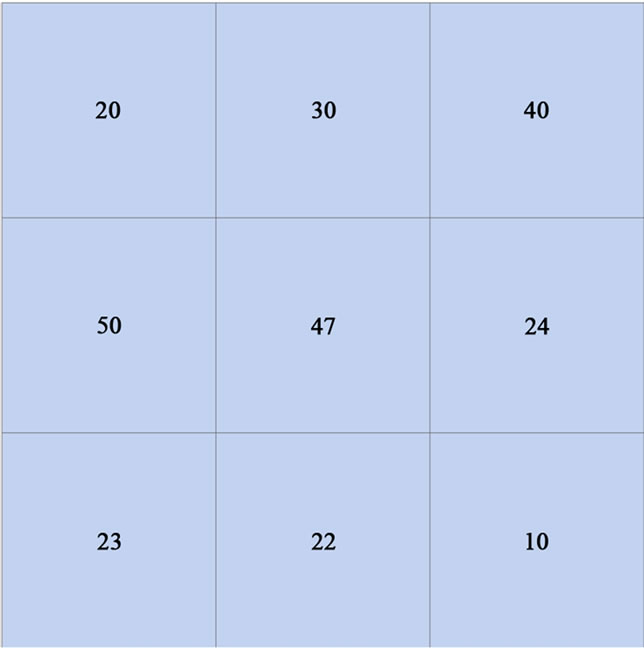
Figure 1. Autocorrelation value map (the number in the polygons are attribute value of each polygon).
whole region express a region’s spatial disparities trend we need to use ESDA local analysis method. Anselin (1994) proposed the local spatial relation index LISA (Local Indicators of Spatial Association), it can show the spatial autocorrelation characteristic for local and each spatial cell. It apportioned global Moran’s I to each region, and the i statistic for each region is:
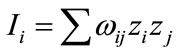 (5)
(5)
where zi, zj is standardization average value, 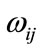 is spatial weighting matrix.
is spatial weighting matrix.
In given significance level, if Ii is obviously positive and zi is greater than 0, and it indicates that the observed value of position I and neighborhood are relatively higher, it is higher to higher cluster, if it is obviously positive and zi is less than 0, and it indicated that the observed value of position I and neighborhood are relatively lower, it is lower to lower cluster, if it is obviously negative and zi is greater than 0, and it indicates that the neighborhood value is far lower to position I, it is higher to lower cluster, if it is obviously negative and zi is less than 0, and it indicates that the neighborhood value is far higher to position i, it is lower to higher cluster.
It is weighted average product for observed value of position i and neighborhood. So global Moran’s I and local Moran’s Ii have follows relation:
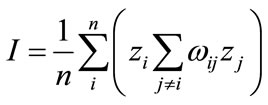 (6)
(6)
The formal condition of LISA statistic and local Moran’s Ii is:
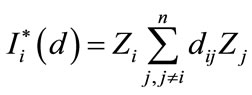 (7)
(7)
We can use Moran scatter plot to describe LISA. All observed value is cross shaft, and all spatial lag value (Wx) is on ordinate axis. All spatial lag value for each region’s observed value is the weighted average value of neighborhood’s observed value. It concretely defined by standardized spatial weighting matrix. The Moran scatter plot can be divided into four quadrants, it is respectively corresponding to four spatial different region spatial type. The right upper quadrant (HH) is the level for region and its neighborhood are higher, and the spatial disparities degree of both is on the small side. The left upper quadrant (HL) is the region’s level is lower than its neighborhood, and the spatial disparities degree of both are comparatively large. The left lower quadrant (LL) is the spatial level for region and its neighborhood are higher, and the spatial disparities degree of both is on the small side. The right lower quadrant (LH) is the region’s spatial level is higher than its neighborhood, and the spatial disparities degree of both is comparatively large.
Example 2 we can compute local Moran’s I of Figure 2, then we can obtain local autocorrelation map, that can be seen in Figure 2. 1) is low and high cluster, 2) is high and high cluster, 3 is high and low cluster in Figure 2.
We can obviously obtain some properties of spatial autocorrelation as below:
1) Patial autocorrelation can only compute continuous attribute value, and can not compute discrete categorical data.
2) Spatial autocorrelation can only compute similarity problem of the whole or each unit’s element, and it can not compute for the similarity between subzones that are composed of several units in whole region.
2.3. Cross-Coefficient
The cross-coefficient r is frequently used to measure linear correlation dimension of two variables in statistics, when 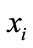 is not all zero and yi is not all zero, the formula of cross-coefficient can obtain from follows formula (8):
is not all zero and yi is not all zero, the formula of cross-coefficient can obtain from follows formula (8):
 (8)
(8)
where r is the cross-coefficient of variables y and x. 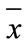 and
and 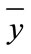 are respectively to the average value of order
are respectively to the average value of order  and
and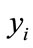 . We can obviously obtain some properties of cross-coefficient as below:
. We can obviously obtain some properties of cross-coefficient as below:
1) Cross-coefficient can only compute continuous attribute value, and can not compute discrete categorical data.
2) The length order of 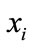 and
and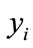 must be the same, if not, it can not compute it.
must be the same, if not, it can not compute it.

Figure 2. Local autocorrelation map (the number in the polygons are Local Moran’s I value of each polygon).
3. Introduction of Rough Sets Theory
3.1. Concept of Rough Sets
Rough sets theory is a mathematical tool for dealing with uncertainty and vague knowledge. And it is a good technique for dealing with uncertainty and fuzzy of GIS data, it is also a good technique for spatial entity relations. There are many references for studying uncertainty and fuzzy of spatial entity, such as Zhang [26,27].
Definition 1. Given knowledge base K = (U, R), for each subset 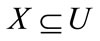 and an equivalence relation
and an equivalence relation , we can define two subsets as follows:
, we can define two subsets as follows:
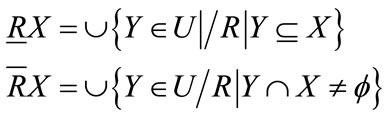 (9)
(9)
where, 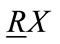 ,
, 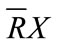 are respectively called lower approximation and upper approximation of set X. This definition is Pawlak rough sets. If set R is subset of universe, then definable set R is R precise set. If R is a not definable set, then R is a rough set. If it has a polygon object X seen in Figure 3, if we used Pawlak describe it, the polygon object X is a fuzzy object in Figure 3.
are respectively called lower approximation and upper approximation of set X. This definition is Pawlak rough sets. If set R is subset of universe, then definable set R is R precise set. If R is a not definable set, then R is a rough set. If it has a polygon object X seen in Figure 3, if we used Pawlak describe it, the polygon object X is a fuzzy object in Figure 3. 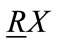 is definitely belongs to X,
is definitely belongs to X, 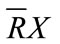 is possibly belongs to X.
is possibly belongs to X.
Example 3. The classification map of Moran’s I can divide into {{1, 3, 7}{2, 4, 5, 8, 9}{6}} according to equivalence class in fig 2. Now it has a subzone X covering {2, 3, 4, 6}, then we can obtain the lower approximation of subzone X is {6}, upper approximation is universe U. All element’s value must be discrete value when we use Pawlak rough sets partition and compute, but GIS object attribute’s value is continuous value in practice, such as slope, population density and so on. Then we should use neighborhood rough sets to compute continuous attribute value.
3.2. GIS Spatial Data Distance Measurement
Geng (2009) suggested We should measure different attribute’s distance in spatial cluster. dij is the distance of attribute level Xi and Xj. The frequently used distance formulas are Minkowski distance, Mahalanobis distance, Canberra distance [28]. We used Mahalanobis distance to define distance of two examples:
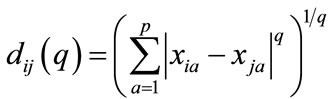 (10)
(10)
when q = 1,that is Absolute distance:
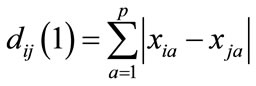 (11)
(11)
when q = 2,that is Euclidean distance:
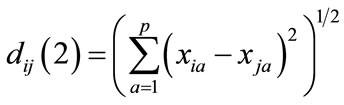 (12)
(12)
when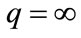 ,that is Chebyshev distance:
,that is Chebyshev distance:
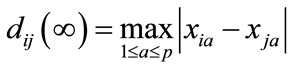 (13)
(13)
Then, we can obviously see diamond is absolute distance, roundness is Euclidean distance, square is Chebyshev distance in Figure 4.
Example 4. Now we consider it has a GIS map level that composed of nine basic units in Figure 5, B and C stand for different attribute. Then it should use absolute distance for measure distance x1 and x2 in attribute B, that we can compute d(x1, x2) = 0.2. It should use Euclidean distance for measure distance x1 and x2 in attribute B, C, that we can compute d(x1, x2) = 0.45. We should dispose source data first in practice, for lack of space, the details will not be dealt with here.
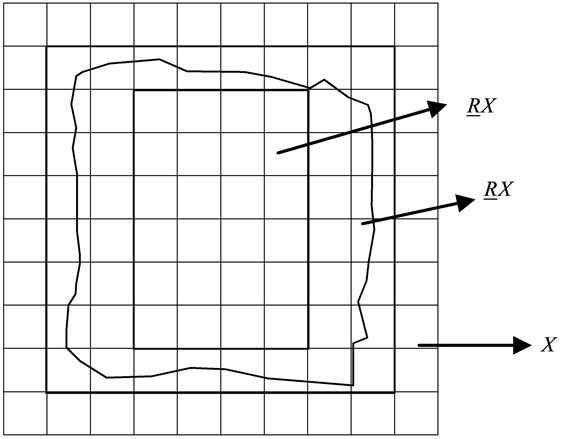
Figure 3. Rough description of area object.
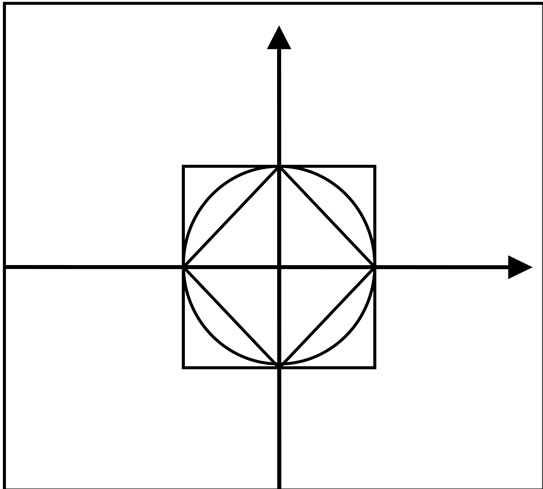
Figure 4. Neighborhood granules in 2-D spaces.
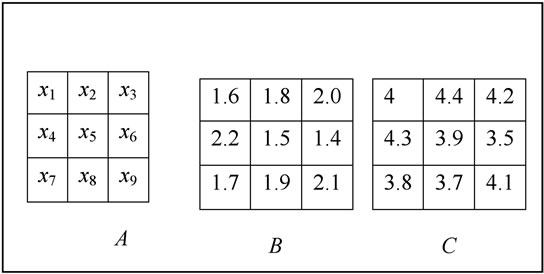
Figure 5. Polygon’s data attribute value map.
3.3. GIS Continuous Data Granulation and Neighborhood Rough Sets
Li [28] suggested granulation and approximation is the basic problem in rough sets and granular computing. Hu [15] found that Pawlak rough sets are based on the equivalence class for discrete value space, and the universe partition from equivalence class can divide into universe space. But for real number space, the attribute value is continuous, such DEM value etc. Obviously, discrete numerical attributes may cause information loss because the degrees of membership of numerical values to discrete values are not considered. Neighborhood structure and order structure are important structure for real number space, so we should work based on neighborhood structure in this paper.
3.3.1. Neighborhood Granulation
There are two methods to define neighborhood, one is defined by the numbers of neighborhood, such as classic k-nearest neighbor methods, the other is defined by distance from one measurement central point to boundary. We used the second method in our work.
Definition 2. Given a N dimension real number space Ω, we call d is a measurement of RN, it usually satisfy follows properties:
1) d(x1, x2) ≥ 0, d(x1, x2) = 0, if and only if x1 = x2,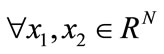 ;
;
2) d(x1, x2) = d(x2, x1), ;
;
3) d(x1, x3) ≤ d(x1, x2) + d(x2, x3),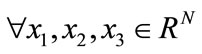 .
.
Then we called (Ω, d) is real number space. And Euclidean distance is a common measurement tool for real number space.
Definition 3. Given a non-null limited set U{x1, x2, x3, 
 xn} in real number space, for every object xi in U, then the δ-neighborhood definition is as follows:
xn} in real number space, for every object xi in U, then the δ-neighborhood definition is as follows:
 (14)
(14)
where δ > 0, 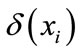 is δ neighborhood information granulation from xi, it for short called as xi neighborhood granulation.
is δ neighborhood information granulation from xi, it for short called as xi neighborhood granulation.
From the measurement properties, we can get three properties about neighborhood information granulation:
1) , because of
, because of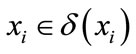 ;
;
2) 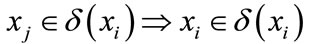
3) 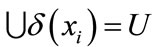
So Given a measurement space (Ω, d) and a non-null limited set U{x1, x2, x3,
 xn}, if δ1 ≤ δ2, then we can get these properties:
xn}, if δ1 ≤ δ2, then we can get these properties:
1) 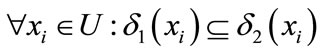
2) 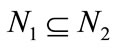
Obviously, neighborhood relations are a kind of similarity relations, which satisfy reflexivity and symmetry properties. Neighborhood relations draw the objects together for similarity or indistinguishability in terms of distances and the samples in the same neighborhood granule are close to each other.
Example 5. Nine polygons are seen in Figure 2, U = {x1, x2, x3, , x9}, and B and C are respectively stand for two attribute level value (such as slope, aspect etc), when we choose value in one dimension attribute, we can use absolute distance. We use f (x, b) to express the value in attribute B for example x , then we can get f (x1, b) = 1.6,f (x2, b) = 1.8,
, x9}, and B and C are respectively stand for two attribute level value (such as slope, aspect etc), when we choose value in one dimension attribute, we can use absolute distance. We use f (x, b) to express the value in attribute B for example x , then we can get f (x1, b) = 1.6,f (x2, b) = 1.8, , f (x9, b) = 2.1. if we assigned the neighborhood threshold is 0.2, because of |f(x1, b) – f(x2, b)| = 0.2 ≤ 0.2, then
, f (x9, b) = 2.1. if we assigned the neighborhood threshold is 0.2, because of |f(x1, b) – f(x2, b)| = 0.2 ≤ 0.2, then
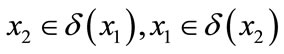 . In this case, we can get
. In this case, we can get
 ,
, ,
,
 .
.
when we get value in two dimension attribute, we should use Euclidean distance, we used f (x, b) to express the value for attribute B, C for example x, if the neighborhood threshold is 0.3. Then we can compute each polygon’s neighborhood in two dimension space,
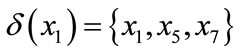 ,
, 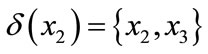 ,
,
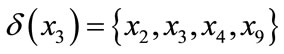 ,
,  ,
,
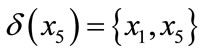 ,
, 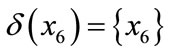 ,
,
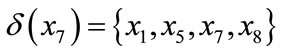 ,
,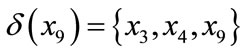 .
.
If it has many attributes, we can compute the distance for examples, and computed the neighborhood for examples.
3.3.2. Neighborhood Approximation
Definition 4. Given a set of objects U{x1, x2, x3, ,xn} and a neighborhood relation R, called D = {U, R} is a neighborhood approximation space [29].
,xn} and a neighborhood relation R, called D = {U, R} is a neighborhood approximation space [29].
Definition 5. Given D = {U, R} and X ⊆ U. For any X ⊆ U, two subsets of objects, it is called lower and upper approximations of X in D= {U, R}, that are defined as follows:
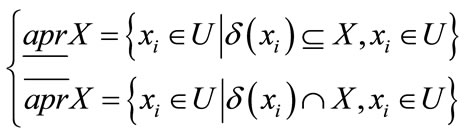 (15)
(15)
Obviously,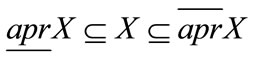 .The positive region of X
.The positive region of X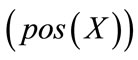 , negative region of X
, negative region of X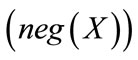 and boundary region of X in the approximation space are defined as follows:
and boundary region of X in the approximation space are defined as follows:
 (16)
(16)
A sample in the decision system belongs to either the positive region or the boundary region of decision. Therefore, the neighborhood model divides the samples into two subsets: positive region and boundary region. Positive region is the set of samples which can be classified into one of the decision classes without uncertainty, while boundary region is the set of samples which can not be determinately classified. Intuitively, the samples in boundary region are easy to be misclassified. In data acquirement and preprocessing, one usually tries to find a feature space in which the classification task has the least boundary region. It is as summarized in Zhang [26].
Example 6. We given two sets X = {x1, x2, x3, x5, x7} and Y={x2, x4, x6} in Figure 5, one sets stand for a group continuous value. Then we can get pos (X) ={x1, x2, x5}, pos (Y) ={x6}, accordingly, we can get the negative region and boundary region for two sets.
Then we can get a map that shown binary classification in a 2-D numerical space in Figure 6, it took it as the first example with “×” label, took it as the second example with “+” label. So we can see x1 is belongs to the lower approximations of the first example, x3 is belongs to the lower approximations of the second example because of its neighborhood are from the second number, x2 is boundary example because of its neighborhood is belongs to the first example and the second example too. The definition is according to our intuitive recognition : 识别;再认;认可;采认for classification problem in real world.
4. Rough Measurement Concept
Definition 7. U is universe, R is equivalence relation of U, 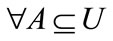 , the rough membership for element
, the rough membership for element  of set A [30], that are defined as follows:
of set A [30], that are defined as follows:
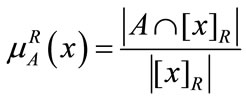 (17)
(17)
The rough membership of x in A is equal to rough membership for fuzzy set x in equivalence class 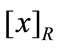 that weakly contains to A. So we can understand rough membership as a coefficient, it describe inaccuracy for
that weakly contains to A. So we can understand rough membership as a coefficient, it describe inaccuracy for 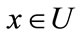 in A.
in A.
The formula (17) is defined for GIS discrete value by Pawlak rough sets membership, but for a continuous value, we can not get equivalence class easily, and we can get this membership from Definition 8.
Definition 8. For GIS continuous value, we use neighborhood rough sets definition for continuous value membership, we defined as follows:
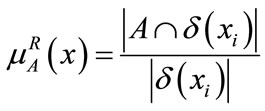 (18)
(18)
The rough membership of x in A is equal to rough membership for neighborhood information granulation 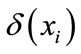 in equivalence class
in equivalence class  that weakly contains to A.
that weakly contains to A.
Definition 9. U is universe, R is equivalence relation of U, 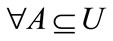 , then a fuzzy set can get from A and R, via:
, then a fuzzy set can get from A and R, via:
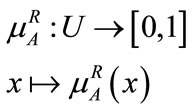 (19)
(19)
Definition 10. Given universe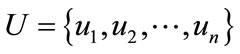 , R is equivalence relation of U, A and B are two rough sets of universe U,
, R is equivalence relation of U, A and B are two rough sets of universe U, 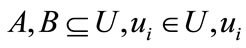 , the rough membership about A, B in equivalence relation R is separately
, the rough membership about A, B in equivalence relation R is separately  and
and 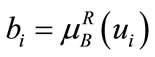 (i = 1, 2,
(i = 1, 2, , n), we can get the membership of A and B in equivalence relation R is separately
, n), we can get the membership of A and B in equivalence relation R is separately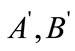 , that defined as follows:
, that defined as follows:
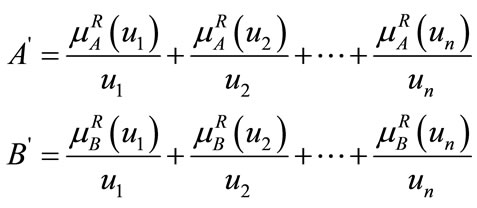 (20)
(20)
Then the similarity of set A and B can get from follows formula: [31].
 (21)
(21)
We used the formula from Shi [32], it is the similarity formula, defined as follows:
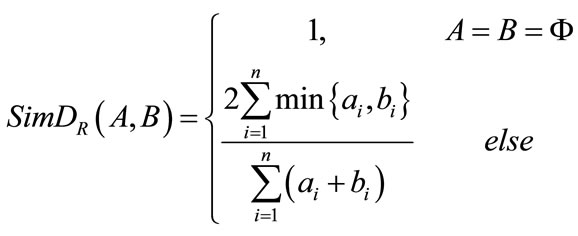 (22)
(22)
Obviously, the higher the similarity of set A and B has, the bigger value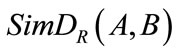 has, vice versa. And it satisfied these properties:
has, vice versa. And it satisfied these properties:
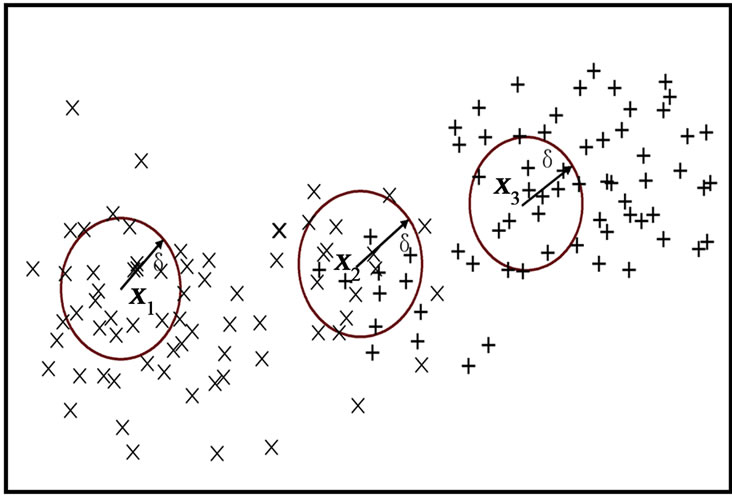
Figure 6. Neighborhood rough approximation in continuous numerical value spaces.
1) ;
;
2)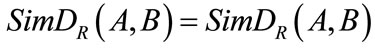 ;
;
3)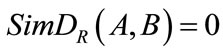 if and only if
if and only if , one value is at least 0 for
, one value is at least 0 for 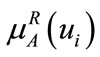 and
and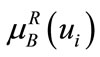 , and set A and B can not be null at the same time.
, and set A and B can not be null at the same time.
5. Case Study
Considering the example seen in Figure 7, it has 100 polygons, the number from left to right, top to down is {1, 2, 3, 100}. Now we have three subzone covering polygons in Figure 7, that is A, B, C, each subzone covered 16 unit polygons, how to measure these three subzone’s similarity, from membership formula, we can get.
100}. Now we have three subzone covering polygons in Figure 7, that is A, B, C, each subzone covered 16 unit polygons, how to measure these three subzone’s similarity, from membership formula, we can get.


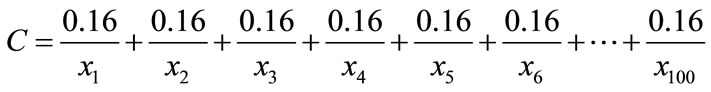
Then the similarity of subzone A and B is:

In a similar way,  ,
,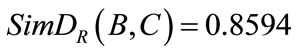 . So the similarity for A and B is less than the similarity of A and C, the similarity for B and C is less than the similarity of A and C.
. So the similarity for A and B is less than the similarity of A and C, the similarity for B and C is less than the similarity of A and C.
Considering the example seen in Figure 8, it has 100 polygons, the number from left to right, top to down is {1, 2, 3, , 100}. Now we randomly evaluate to every polygon’s continuous value (1 - 100), specific value seen in Figure 8, we have three subzone covering polygons in Figure 8, that is A, B, C, each subzone covered 16 unit polygons, how to measure these three subzone’s similarity for continuous value .
, 100}. Now we randomly evaluate to every polygon’s continuous value (1 - 100), specific value seen in Figure 8, we have three subzone covering polygons in Figure 8, that is A, B, C, each subzone covered 16 unit polygons, how to measure these three subzone’s similarity for continuous value .
For continuous value in Figure 8, we used absolute distance formula because it only has one attribute, we give threshold δ = 10 for neighborhood granulation. Then we can get each polygon’s distance from others in turns, and get each polygon’s neighborhood information granulation. Such as, the neighborhood information granulation of polygon 1 is {1, 10, 27, 28, 34, 50, 51, 65, 68, 75, 94, 98, 99, 100}, the rough membership for subzone A is 1/14, the rough membership for subzone B is 2/14, the rough membership for subzone C is 2/14. From continuous value membership formula, we can get
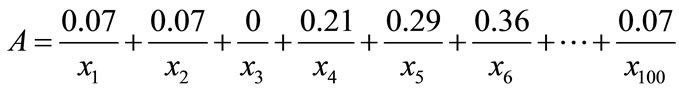
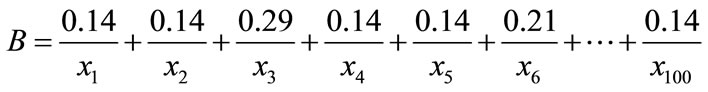

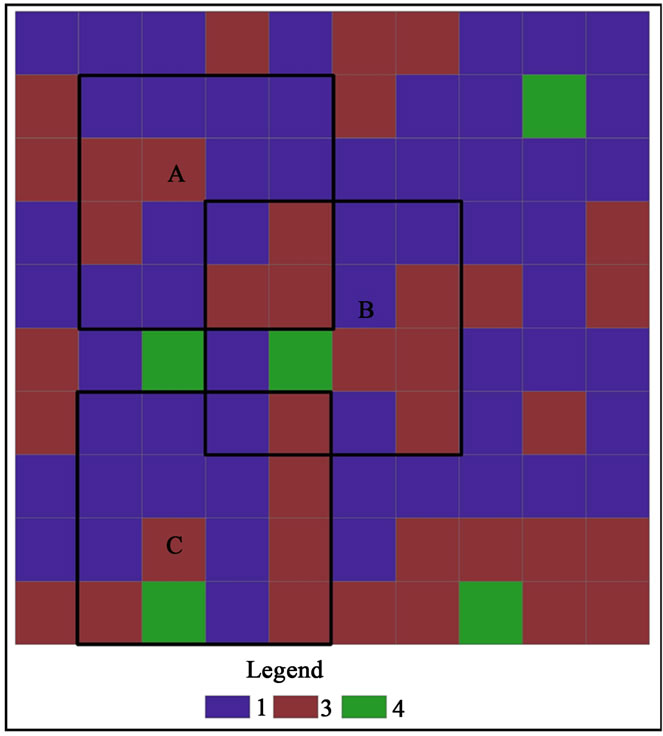
Figure 7. All-around polygon classification and subzone map.
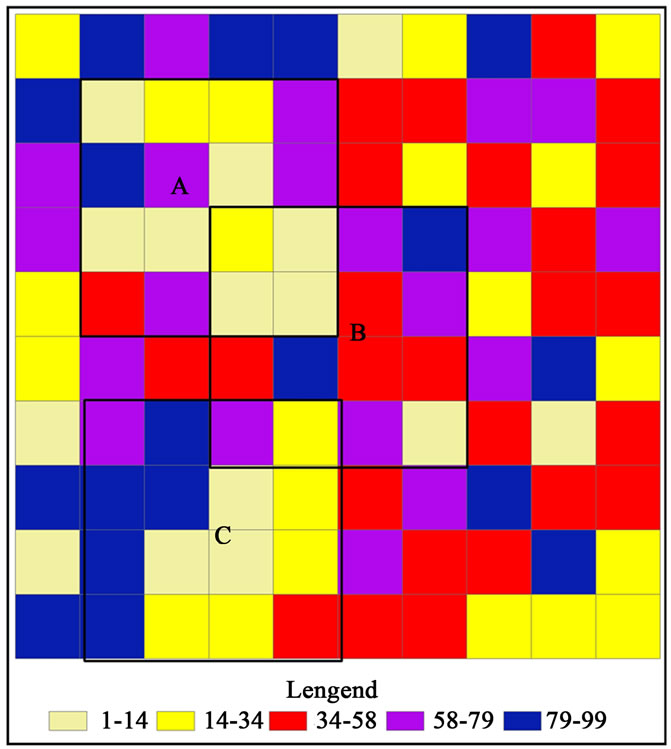
Figure 8. All-around polygon classification and subzone map.
Then the similarity of subzone A and B is:

In a similar way, 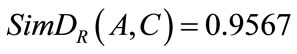 ,
, . So the similarity for A and C is less than the similarity of A and B, the similarity for B and C is less than the similarity of A and C.
. So the similarity for A and C is less than the similarity of A and B, the similarity for B and C is less than the similarity of A and C.
If used spatial autocorrelation to measure the subzone similarity for above case, we can find it can not measure Figure 7, because the value is discrete. And the spatial autocorrelation can only compute continuous attribute value, it can not compute for the similarity between subzones that are composed of several units in whole region. The cross-coefficient can not measure Figure 7 too, because the value is discrete. And if the subzone in map is not equal length for continuous value, it can not measure similarity too. The rough measurement based on membership function solved this problem well.
6. Conclusion and Future Work
This paper used rough membership measure similarity problem for different subzone. Because Moran’s I can only measure universe or each unit’s spatial autocorrelation, it can not measure subzone, so our method can compute GIS subzone similarity based on universe. And for continuous value, we used distance function and neighborhood rough sets to divide continuous value’s upper and lower approximation and classification problem, then we put forward a rough membership function based on neighborhood information granulation. At last, we used rough similarity measurement formula to measure GIS subzone similarity problem, this method can provide a new direction for GIS point group or others’ object group similarity measurement. Our future work should study object group similarity based on different distribution, and for similarity problem based on rough entropy.
7. Acknowledgements
The author would like to thank the project sponsored by the scientific research foundation of GuangXi University (Grant No.XTZ110584).
REFERENCES
- W. R. Tobler, “A Computer Movie Simulating Urban Growth in the Detroit Region,” Economic Geography, Vol. 46, No. 2, 1970, pp. 234-240. doi:10.2307/143141
- A. D. Cliff and J. K. Ord, “Spatial Autocorrelation,” Pion, London, 1973.
- J. F. Wang, L. F. Li and Y. Ge, “A Theoretic Framework for Spatial Analysis,” Acta Geographica Sinica, Vol. 55 No. 1, 2000, pp. 92-103.
- F. Chen and D. S. Du, “Application of the Integration of Spatial Statistical Analysis with GIS to the Analysis of Regional Economy,” Geomatics and Information Science of Wuhan University, Vol. 27, No. 4, 2002, pp. 391-396.
- L. Anselin, “Local Indicators of Spatial Association: LISA,” Geographical Analysis, Vol. 27, No. 2, 1995, pp. 93-115. doi:10.1111/j.1538-4632.1995.tb00338.x
- D. Y. Li and C. Y. Liu, “Artificial Intelligence with Uncertainty,” Journal of Software, Vol. 15, No. 11, 2004, pp. 1583-1594.
- Z. Pawlak, “Rough Sets,” International Journal of Computer and Information Sciences, Vol. 11, 1982, pp. 341- 356.
- Z. Pawlak, “Rough Sets Theoretical Aspects of Reasoning about Data,” Kluwer Academic Publishers, Dordrecht, 1991.
- Z. Pawlak, “Rough Set Theory and Its Application to Data Analysis,” Cybernetics and Systems, Vol. 29, No. 9, 1998, pp. 661-668. doi:10.1080/019697298125470
- R. Slowinski, “A generalization of the in Discernibility Relation for Rough Sets Analysis of Quantitative Information,” Decisions in Economics and Finance, Vol. 15, No. 1, 1992, pp. 65-78. doi:10.1007/BF02086527
- P. Srinivasan, “The Importance of Rough Approximations for Information Retrieval,” International Journal of Man-Machine Studies, Vol. 34, No. 5, 1991, pp. 657-671. doi:10.1016/0020-7373(91)90017-2
- T. Beaubouef, F. Petry and B. Buckles, “Extension of the Relational Database and Its Algebra with Rough Sets Techniques,” Computational Intelligence, Vol. 11, No. 2, 1995, pp. 233-245. doi:10.1111/j.1467-8640.1995.tb00030.x
- X. B. Yang, D. J. Yu and J. Y. Yang, “Dominance-Based Rough Set Approach to Incomplete Interval-Valued Information System,” Data & Knowledge Engineering, Vol. 68, No. 11, 2009, pp. 1331-1347. doi:10.1016/j.datak.2009.07.007
- T. Beaubouef, F. E. Petry and R. Ladner, “Spatial Data Methods and Vague Regions: A Rough Sets Approach,” Applied Soft Computing, Vol. 7, No. 1, 2007, pp. 425-440. doi:10.1016/j.asoc.2004.11.003
- Q. H. Hu, D. R. Yu and Z. X. Xie, “Numerical Attribute Reduction Based on Neighborhood Granulation and Rough Approximation,” Journal of Software, Vol. 19, No. 3, 2008, pp. 640-649. doi:10.3724/SP.J.1001.2008.00640
- H. Xie, H. Z. Cheng and D. X. Niu, “Discretization of Continuous Attributes in Rough Sets Theory Based on Information Entropy,” Chinese Journal of Computers, Vol. 28, No. 9, 2005, pp. 1570-1574.
- R. Jensen and Q. Shen, “Semantics-Preserving Dimensionality Reduction: Rough and Fuzzy-Rough-Based Approaches,” IEEE Transactions on Knowledge and Data Engineering, Vol. 16, No. 12, 2004, pp. 1457-1471. doi:10.1109/TKDE.2004.96
- D. Dubois and H. Prade, “Rough Fuzzy Sets and Fuzzy Rough Sets,” International Journal of General Systems, Vol. 17, No. 2, 1990, pp. 191-209. doi:10.1080/03081079008935107
- Q. H. Hu, D. R. Yu and Z. X. Xie, “Fuzzy Probabilistic Approximation Spaces and Their Information Measures,” IEEE Transactions on Fuzzy Systems, Vol. 14, No. 2, 2006, pp. 191-201. doi:10.1109/TFUZZ.2005.864086
- D. S. Yeung, D. G. Chen, et al., “On the Generalization of Fuzzy Rough Sets,” IEEE Transactions on Fuzzy Systems, Vol. 13, No. 3, 2005, pp. 343-361. doi:10.1109/TFUZZ.2004.841734
- Q. H. Hu, D. R. Yu and Z. X. Xie, “Information-Preserving Hybrid Data Reduction Based on Fuzzy Rough Techniques,” Pattern Recognition Letters, Vol. 27, No. 5, 2006, pp. 414-423. doi:10.1016/j.patrec.2005.09.004
- R. Slowinski and D. Vanderpooten, “A Generalized Definition of Rough Approximations Based on Similarity,” IEEE Transactions on Knowledge and Data Engineering, Vol. 12, No. 2, 2000, pp. 331-336. doi:10.1109/69.842271
- T. Y. Lin, “Data Mining and Machine Oriented Modeling: A Granular Computing Approach,” Applied Intelligence, Vol. 13, No. 2, 2000, pp. 113-124. doi:10.1023/A:1008384328214
- R. M. Wu and X. H. Zhang, “A Research on the Difference Measures of Rough Fuzzy Sets,” Journal of Southwest University for Nationalities (Natural Science Edition), Vol. 35, No. 6, 2009, pp. 1139-1142.
- Y. Y. Guan and H. K. Wang, “Measures of Rough Similarity between Sets,” Fuzzy Systems and Mathematics, Vol. 20, No. 1, 2006, pp. 134-139.
- W. X. Zhang, W. Z. Wu and J. Y. Liang, “Rough Set Theory and Method,” Science Press, Beijing, 2005.
- X. P. Geng, X. C. Du and P. Hu, “Spatial Clustering Method Based on Raster Distance Transform for Extended Objects,” Acta Geodaetica et Cartographica Sinica, Vol. 38, No. 2, 2009, pp. 162-168.
- X. F. Li and J. Li, “Data Mining and Knowledge Discovery,” Higher Education Press, Beijing, 2003.
- Y. Zhou, H. Lin and Y. B. Cui, “The Study under Rough Relation and It’s Neighbor Relation,” Computer Science, Vol. 31, No. 10A, 2004, pp. 61-63.
- F. C. Liu, “Similarity Measure and Similarity Direction between Fuzzy Rough Sets,” Computer Engineering and Applications, Vol. 35, 2005, pp. 63-66.
- H. K. Wang, Y. Y. Guan and K. Q. Shi, “Measure of Similarity between Rough sets and Its Application,” Computer Engineering and Applications, Vol. 31, 2004, pp. 39-40.
- Z. H. Shi and Y. P. Lian, “Measure of Similarity between Rough Sets Based on Inclusion,” Research of Mathematic Teaching-Learning, Vol. 2, 2008, pp. 53-54.

