Received 7 January 2015; accepted 25 January 2015; published 29 January 2015

ABSTRACT

Usually financial crises go along with bubbles in asset prices, such as the housing bubble in the US in 2007. This paper attempts to build a mathematical model of financial bubbles from an econophysics, and thus a new perspective. I find that agents identify bubbles only with a time delay. Furthermore, I demonstrate that the detection of bubbles is different on either the individual or collective point of view. Second, I utilize the findings for a new definition of asset bubbles in finance. Finally, I extend the model to the study of asset price dynamics with news. In conclusion, the model provides unique insights into the properties and developments of financial bubbles.

Keywords:

Financial Bubbles, Econophysics, Wave Equation, Financial Crises

1. Introduction

The phenomenon of a financial bubble is debated in economics for centuries. There are several important questions: What is a bubble? How can we identify a bubble? What is the root cause of a bubble and what triggers a bubble burst? So far, different economic and mathematical models study different issues of bubbles. However to my knowledge, there is no consistent model that addresses all issues at once. In addition, the complexity in financial markets due to social interaction and behavioural elements makes the study of those bubbles difficult.

This paper attempts to develop a new model of financial bubbles. My model utilizes the idea of particle dynamics in physics. I translate this idea into the dynamics of financial assets without relying on stochastic and martingale theory [1] . Hence, I intend to throw light on the bubble definition, detection, and dynamics without using stochastic theory. I find that the model is tractable and, at the same time, provides valuable evidence. First, I demonstrate that traders always recognize bubbles with a time delay. Second, I study the properties of bubble detection in detail. It turns out that the modeling of herd behaviour and the impact of news are major forces of financial bubbles. Third, I analyze news of asset prices and the relationship to financial bubbles. At the end, I develop some regulatory policy recommendations for financial markets.

The remainder of the paper is structured as follows. Section 2 discusses the different forms of financial bubbles and presents a literature review. In Section 3, I derive the mathematical model and study the main implications. Section 4 extends the model and studies the impact of news. Finally, Section 5 provides concluding remarks.

2. Motivation and Literature Review

Let me start with a quote by Charles MacKay about the forces of financial bubbles in general: “Men, it has been well said, think in herds; it will be seen that they go mad in herds, while they only recover their senses slowly, and one by one.” No doubt, herd behaviour turns out to be important during almost all financial bubbles. Thus it was studied in the economic literature for decades. In general, there are different types of herd behaviour and they are characterized by imperfect information, a systematic bias in expectations, and regulatory arbitrage due to perverse incentives.

The need for better models in this field has to do with the tremendous social costs of a bubble burst [2] [3] . Indeed, a bubble exacerbates volatility, destabilize markets and increase the fragility of the overall financial system [4] . In the economics literature there are three different lines of modeling but the reference point is always the seminal work by [5] .

First, economists have analyzed “information-based” or “rational” herd behaviour. That research is pioneered by DeLong et al. [6] , Froot et al. [7] , and Lux and Marchesi [8] . They argue that individuals observe the action of each other but not the private information that they receive. The arrival of too little information and idiosyncratic news leads to either rational but always erratic decision-making. Indeed, agents do not realize that they are in a financial bubble due to flawed expectations and imperfect information. This leads to fragile financial markets in the end. There are several modeling variants of information-based herd behaviour in economics [9] -[13] . For instance, Maug and Naik [14] find that risk avers investors’ that have imperfect information about stock returns tend to follow a herd rather soon.

A second line of literature in economics argues for “reputation-based herding”. This was first explored by Scharfstein and Stein [15] . They show that uncertainty about the own ability leads to path-dependency; i.e. you follow a naive trend or a heuristic. Commonly, investors use heuristics in finance, such as a rule-of-thumb. Therefore, skilled agents with reputation in finance are less prone to herd behaviour and financial bubbles. A third approach is “compensation-based herding”. That form of herd behaviour appears if an investors’ compensation depends on the performance to others.

This paper develops a unique link between the different types of herd behaviour and a general “Model of Financial Bubbles”. To analyze the complex financial dynamics, I build a mathematical model based on particle physics. In fact, there exist an obvious parallel of both particle and financial dynamics. The dynamics of both systems is based on the interaction of single elements/agents that lead to a collective outcome. From an aggregate perspective, the frequent events of traffic jams are often the result of uncoordinated interaction of individual’s at overcrowded highways and not always a car accident. Interestingly, this is similar to the root cause of herd behaviour in financial markets. Consequently, a financial bubble, i.e. a massive price increase (decrease), can be caused by a large number of buying (selling) individuals, especially if they build a herd. Thus, bubbles can come into existence without any change of the fundamental value. The ups and downs of asset prices attract similar agents and thus form a herd. Soon later, I obtain a bubble or crash. Unfortunately, the collective behaviour creates even more volatility, higher risks, and massive welfare losses. A second parallel between physics and financial bubbles is the impact of news as a root cause or trigger of a bubble. Ad-hoc news either positive or negative can be compared to an unforeseeable red light or traffic flows via an exit or entrance to a highway. Hence, the main objective of my model is twofold: 1) build a coherent model and 2) find new implications for empirical finance in future.

There is also a large descriptive literature about collective behaviour in speculative bubbles [16] -[19] . The model by Galbraith [20] identifies accelerating bubbles as a precursory pattern for essentially all crashes. A similar result is found by Kindleberger and Fransman [21] . Although these papers provide interesting insights, they have limitations. They cannot sufficiently explain the causes and triggers of both bubbles and crashes. One reason for this limitation is due to the methodological disadvantage of economic models. The economic models utilize the individualistic and equilibrium methodology. These two elements have a serious downside in the study of complex dynamics and social interactions [22] . Therefore, my econophysic model provides a new per- spective and is ready to analyse complex dynamics and social interactions.

3. Econophysics Model

The financial asset price dynamic is denoted by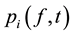. This is a function of asset i dependent on two variables: the fundamental price vector f and time t. The benefit-loss-rate (BLR) of each asset i is defined by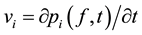. The BLR can be interpreted as the price change or the speed of asset i. The acceleration of the price change, i.e. the rate of change of the BLR, is given by the second derivative, such as. There are different ways to define bubbles or herd behaviour. Obviously, a financial bubble is closely con- nected to a high BLR, , and a high rate of change of the BLR,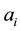. Hence, I define a unique benefit-loss-field (BLF)

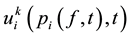(1)

where k captures the agents’ expectation or reputation level. I assume 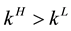and the H denotes a high and L a low reputation level respectively. The existence of a BLF implies that for each price process, 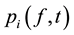, exists only one unique benefit or loss. Thus, this model does not simultaneously allow different BLF for the same asset price dynamic; i.e. 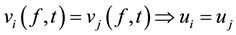for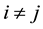. However, I assume different dynamics for the rate of change,. This assumption is consistent with financial market dynamics [23] . At the beginning, I study the market dynamics along with continuous functions without jumps. This is known as the continuum hypothesis. In addition, let me define the following variables:

Definition 1. Trading volume (flow) of asset i is defined as the amount of buy and sell orders (number of trades) times the buy and sell price per day. It is denoted by the function.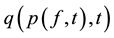

Definition 2. Trading density of asset i is defined as the number of trades within a certain price range. It is denoted by.

Next, based on both definitions, I define a fundamental relationships:

Definition 3. There exists a relationship between trading volume, trading density and the benefit-loss-field, such as

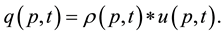(2)

The last equation is a fundamental law in applied physics and in my econophysics model on financial assets. In the following subsections, I derive the model and study the identification of a financial bubble.

3.1. Derivation of Model Equation

Next, I consider the two fundamental variables 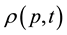and. The function can be measured in reality, while the BLF, , is unobservable. As defined above, the motion of each asset price satisfies a first-order differential equation, such as

(3)

Solving this equation would determine the asset price for which an agent is willing to buy or sell at a later time under a uniform stock market. However, finding the function is not an easy task in reality. Therefore, I choose a different approach. Suppose, the aggregate number of trades is equal to N. Then, you can define N as the integral of the trading density in the given price range and, as

(4)

In general, the number of trades change over time. It increases with the inflow of buying agents at the lower bound and it decreases with the outflow of sellers at the upper price-limit. Hence, I obtain

(5)

Combining Equations (4) and (5), per definition yields

(6)

The last equation can be labelled a “conversation law”. Hence, the equation denotes that the number of trades in a certain price range is equal to the difference of the trading volume in this price range. Starting with that equation, I derive the model. Consider the integral conversation law over a small interval from to. Equation (6), yields

(7)

Now, divide by and take the limit as:

(8)

The right-hand side of that equation is the first derivative of with respect to a, i.e.. Next, let me redefine the left-hand side with a new function. I introduce the function, the number of trades between any price and. I obtain

(9)

The average number of trades in the defined price interval is given by

(10)

In limit for, the right-hand side obtains. Thus, I can rewrite Equation (10), as

(11)

The left-hand side of Equation (8) equals now. The following equation holds for all a. Therefore, it is more appropriate to replace a by p. I finally obtain

(12)

which is a wave equation in form of a partial differential equation (PDE). This equation can be rewritten with the help of the fundamental law from Equation (2), where q is defined as. Hence, trading volume is a function of the density, , and thus I obtain a non-linear PDE of the form

(13)

Solving this PDE requires further assumptions. Suppose that the BLF is defined as a function of the density, such as. Moreover, this function has the following properties: 1), where . That is intuitively clear because the higher the reputation (ability) the greater the likelihood of gains and hence the level of the BLF. 2) The BLF and thus the profits are zero in a perfect competitive market according to standard economics;. Hence, agents are price-taker in this market environment. 3) Logically

the function value, , is declining in. Consequently, the first derivative is negative:.

Figure 1 illustrates these properties in a linear model graphically. If the trading density is low, then the BLF is maximal, i.e. assets with a limited amount of trades have a bigger potential for benefits (or losses) by a few active traders. This assumes that a low amount of orders significantly change the price in spare markets. Simultaneously, this assumption indicates either a high degree of asymmetric information or uncertainty. Both problems are revealed by a low trading density. In the other extreme of maximal trading density, I obtain a market environment with “full information” and that would imply a benefit (loss) of almost zero. Hence, in this market environment agents are price-taker.

3.2. Solution

The solution of the non-linear PDE Equation (13) determines the trading density and thus the price at all future times. Hence, I solve the following initial value problem

(14)

This problem requires a linear approximation. Suppose the density is uniform, then it can be approximated as

(15)

where, and is called the “perturbed” trading density. For, I obtain

(16)

where. Differentiation of Equation (14) in respect to, result in

(17)

Taylor-series approximation of the second term, yields

(18)

where. Now, I have transformed the non-linear PDE into a linear-homogenous partial differential equ- ation of the form:

(19)

I solve this PDE via variable transformation. Use both and, and rewrite it in the following terms:

(20)

Substitute both findings in Equation (19), yields finally

(21)

Proposition 1. The general solution of the PDE in Equation (19) and (21), is given as .

Proof. First, compute

and then substitute both expressions in Equation (19):.

3.3. Definition of a Financial Bubble

The solution of the model enables me to define a financial bubble in general.

Definition 4. A bubble is defined as a trading density greater than or accordingly by. Figure 2 illustrates the definition graphically. Let me use this definition and discuss the implications.

Proposition 2. The existence of a bubble implies that the benefit-loss-field (BLF) is different to the specific BLR of an asset.

Proof. Due to.

A negative slope of the BLF is a necessary and sufficient condition for a bubble in my model. In this constellation all traders buy (sell) the respective asset and that lowers the risk of the individual’s BLF. However, an increasing trading density creates herd behaviour and finally a financial bubble in the overall market (Figure 2).

Proposition 3. In general, a bubble is defined by an upper limit for. In other words, the left-hand

side is less than the BLF.

Proof. If then and therefore.

This proposition demonstrates that a bubble can be characterized as a social interaction problem. Hence, a financial bubble is not just determined by individual rationality or irrationality as assumed in economic models. On the contrary, more buyers automatically indicate a higher trading density and higher risk for an exuberance. But from the individual point of view it is the other way round. A high density imply a small price movement and thus a lower risk and higher willingness to buy (sell) assets. This interaction and finally the imbalance of both mechanisms trigger a financial bubble. This new insight is in line with findings in sociology and psychology, for instance in the social system theory [22] , and thus underlines the interdisciplinary character of the model.

4. Extended Model with Jumps

Finally, I model the impact of “news” in financial markets with bubbles. I utilize the idea of a “jump-disconti- nuity”. In this case, I obtain

(22)

This integral is well defined if even has a jump-discontinuity. A jump can be interpreted as a trading stop or news. In connection with Equation (2), , the derivation of Equation (22) to dt yields

(23)

Let’s assume that the trading density changes on both ends of the interval at the same amount,

. Set Equation (23) equal to zero, results in and after a transformation, I obtain

(24)

where and. Substituting this back in Equation (23), together with Equation (2), yields

(25)

Proposition 4. A financial bubble is characterized by a negative BLF in respect of time:.

Proof. Use the properties of the function together with Equation (25). Compute the first derivative, I obtain.

Consequently, the proposition confirms that good news imply a jump with a decline in the change of asset prices (BLR) and thus a lower probability of a bubble burst. Even if the result seems to be counterintuitive at first, it has a rational. News reduce asymmetric information and thus lowers the BLF. This reduces the market reaction time. In other words, the bubble may burst in case of small price jumps. Consequently, efficient markets with many news may trigger only small financial bubbles, but inefficient markets (=high asymmetric information) with little news may trigger huge financial bubbles. The solution of the ODE (Equation (25)), demonstrates the evolution of the asset price with news and it yields

(26)

This equation explains the fact that with increasing time, t, the asset price declines automatically due to the lag of news. Therefore, more agents enter the market and buy/sell assets. In the end, this leads to herd behaviour and a financial bubble.

5. Conclusion

This paper attempts to explain the major properties and developments of financial bubbles from an econophysics point of view. I utilize a new theoretical model to detect ex ante financial bubbles. This model makes the complexity tractable without stochastic and martingale theory. In general, this approach has several advantages. First, it is a simple model and uniquely defines a financial bubble. Second, the model is general and thus explains the origins and developments of bubbles, too. Third, the model contains novel implications for empirical studies on financial bubbles. Finally, and most importantly, this model enables you to study the effect of news on financial bubbles for the first time.

Acknowledgements

I thank the editor and two anonymous referees for their helpful comments and suggestions. Research is funded by the RRI―Reutlingen Research Institute. This support is greatly appreciated.

References