Natural Science
Vol.6 No.7(2014), Article ID:45345,11 pages DOI:10.4236/ns.2014.67049
An Extended Interpretation of the Concept of Entropy Opening a Link between Thermodynamics and Relativity
Jean-Louis Tane
Formerly with the Department of Geology, University Joseph Fourier, Grenoble, France
Email: tanejl@aol.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 3 December 2013; revised 3 January 2014; accepted 10 January 2014
ABSTRACT
It is well known that thermodynamics raises conceptual difficulties. Far to be limited to students having to learn the subject, this impression is sometimes mentioned by specialists themselves who confess not being totally sure of the consistency of the thermodynamic theory, despite the fact that its practical usefulness is indisputable. The present paper deals with this interesting question and leads to the idea that there is an imperfect convergence between the way of using the thermodynamic tool and the way of understanding its significance. Illustrated by a very simple example, the discussion can be followed by every scientist having the fundamental basis in thermodynamics. The suggested hypothesis is that the Einstein mass-energy relation is closely associated to the concept of entropy, opening a link between thermodynamics and relativity.
Keywords:Thermodynamics, Reversibility, Irreversibility, Energy, Entropy, Einstein’s Mass-Energy Relation, Relativity, Gravitation

1. Evocation of the Problem in Some Thermodynamics Textbooks
The thermodynamics textbooks quoted [1] [2] in the reference list given below were written for geologists by scientists specialized in physical-chemistry. In the preface of Reference [1] , D. K. Nordstrom and J. L. Munoz mention a testimony of the famous physicist Arnold Sommerfeld, explaining that he was reluctant to write a treatise of thermodynamics—as suggested to him by his colleagues—because, although he was able to use the theory, he was not sure to perfectly understand it. In Reference [2] , G. M. Anderson and D. A. Crerar present a similar thought by Howard Reiss, evoking, in the preface of his own book on the subject [3] , “the almost certain truth that nobody (authors included) understands thermodynamics completely” and adding: “the writing of a book therefore becomes a kind of catharsis in which the author exorcises his own demons of incomprehension and prevents it from occupying the soul of another”.
For the reader confronted with it, this kind of information is received as an invitation to think about the problem and try to participate to the search for a solution.
2. A Basic Remark Concerning the Concepts of Reversibility and Irreversibility
The concepts of reversibility and irreversibility, that are specific to thermodynamics, can be summarized through the very simple experimental context described below (Figure 1).
The considered system is a gas (light grey) contained in a cylinder equipped with a mobile frictionless piston (black). We suppose that this system can exchange work and heat with the surroundings, and our objective is the thermodynamic interpretation of the process that consists, for the gas, in passing from state 1 (conditions P1, V1, T1) to state 2 (P2, V2, T2). The symbols P, V, T, designate respectively the pressure, volume, and temperature of the system. The passage from state 1 to state 2 is due to a complementary weight placed on the piston, for example a small amount of sand (dark grey), with the consequence that both the external pressure Pe and the internal pressure Pi, pass from an initial value P1 to a final value P2. To simplify the problem, we consider here that the temperatures obey the relation T2 = T1 = Te where Te represents the temperature of the surroundings which is supposed constant.
The sand can be placed on the piston very rapidly or very progressively, so that the level of irreversibility of the process is not the same in all cases. Nevertheless, according to the conventional understanding of the first law of thermodynamics, the change in internal energy of the gas, designated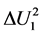 , is supposed to have always the same value. This proposal—which constitutes one of the fundamental postulates of the theory—is classically written:
, is supposed to have always the same value. This proposal—which constitutes one of the fundamental postulates of the theory—is classically written:
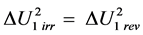 (1)
(1)
or, in differential notation:
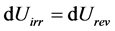 (2)
(2)
which means, implicitly, that dU is an exact differential.
By definition, the change in internal energy dU is the sum of the different kinds of energies that can be involved in the experimental context examined. As the ones considered here are limited to heat (dQ) and work (dW), the term dU can be written under the form:
 (3)
(3)
where the symbols d represent the fact that dQ and dW, contrary to what is admitted for dU, are not necessarily exact differentials.
Among the basic tools of physics is the well-known mechanical equation:
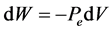 (4)
(4)
which defines the work received or provided by a system whose volume varies by a quantity dV under the effect of an external pressure Pe.
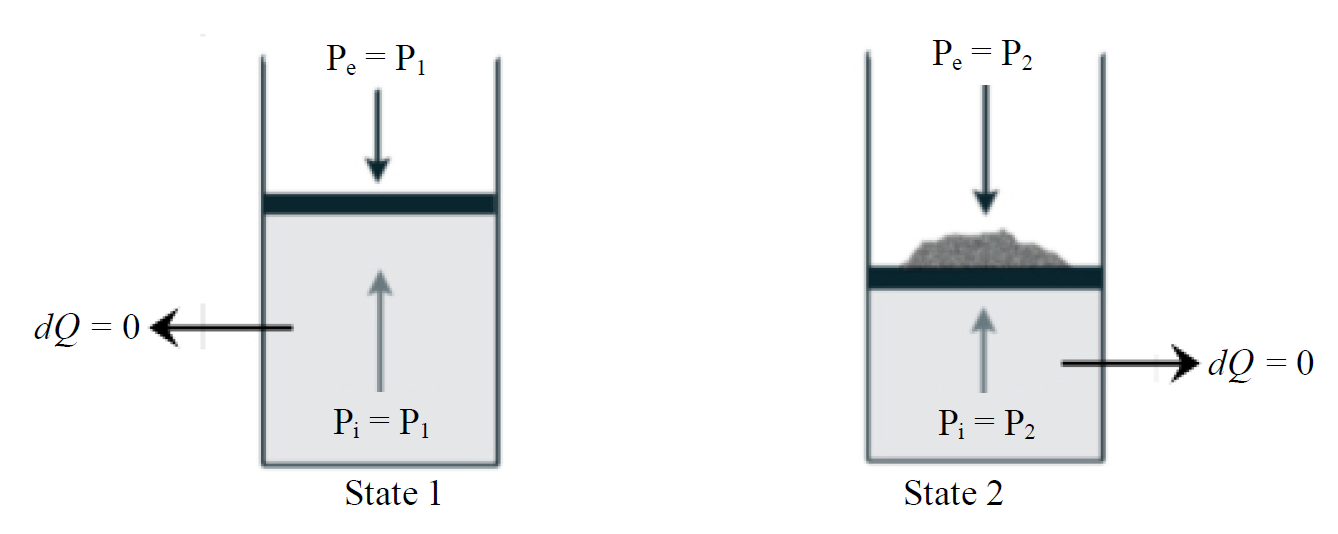
Figure 1. Schematic representation of the considered system.
Equation (4) refers to the general case of an irreversible exchange of work, implying that the external pressure Pe is different from the internal pressure Pi. This exchange of work can therefore be designated as:
 (5)
(5)
In conditions of reversibility, the external pressure Pe tends to be equal—at each moment of the process—to the internal pressure Pi, so that Equation (4) takes the form:
 (6)
(6)
For a given value of dV, this difference between dWirr and dWrev can be written:
 (7)
(7)
that is:
 (8)
(8)
Referring to the schematic representation given in Figure 1, we see that dV is negative when Pi < Pe and positive when Pi > Pe. Consequently, the product dV(Pi – Pe) is itself always positive, leading to the conclusion:
 (9)
(9)
Another possible writing of Equation (9) is therefore:
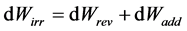 (10)
(10)
where  means
means  and has as a positive value.
and has as a positive value.
NB: It is important to note that in some thermodynamics textbooks, for instance the one written by M. M. Abbott and H. C. Van Ness [4] , the relation between dWirr and dWrev is noted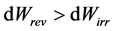 . The reason is that the work taken in consideration is not the one done on the system (convention of thermodynamicians, corresponding to the definition dW = –PdV), but the one done by the system (convention of engineers, corresponding to the starting definition dW = PdV). This inversion has no effect on the value of dU, because in the same time, the definition adopted for dU is dU = dQ – dW. To avoid any confusion, the present paper is exclusively based on the convention of thermodynamicians. The starting definitions being those given by Equations (4), (5) and (6), the concluding information to keep in mind is the one given by Equations (9) and (10).
. The reason is that the work taken in consideration is not the one done on the system (convention of thermodynamicians, corresponding to the definition dW = –PdV), but the one done by the system (convention of engineers, corresponding to the starting definition dW = PdV). This inversion has no effect on the value of dU, because in the same time, the definition adopted for dU is dU = dQ – dW. To avoid any confusion, the present paper is exclusively based on the convention of thermodynamicians. The starting definitions being those given by Equations (4), (5) and (6), the concluding information to keep in mind is the one given by Equations (9) and (10).
We have recalled above (Equation (2)) that in the conventional interpretation of the first law, when a system passes from a state 1 to a state 2, its change in internal energy is the same, implying the equality dUirr = dUrev. By confronting this information with the relation dU = dQ + dW (Equation (3)), we see that the condition dWirr > dWrev (Equation (9)) implies itself that the exchange of heat between the system and the surroundings would obey the inequality:
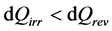 (11)
(11)
In thermodynamics textbooks, the concept of heat exchange is closely linked to that of change in entropy, whose definition is introduced in the chapters dealing with the second law. The subject is often presented under the summarized form hereafter.
In conditions of reversibility, the change in entropy is linked to the change in heat and the absolute temperature T by the relation:
 (12)
(12)
In condition of irreversibility, the corresponding equation becomes:
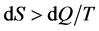 (13)
(13)
When the reader is confronted with Equations (12) and (13), and receives the additional information that S is a state function, implying that dS has the same value in both equations, he is tempted to think that dQ represents dQrev in Equation (12) and dQirr in Equation (13). In such conditions, his first impression is that the relation dQirr < dQrev expected by Equation (11) seems to be verified. Returning to Figure 1 he keeps this impression, because having in mind what happens in the context of a bicycle pump, he knows that the additional energy dWadd that appears in conditions of irreversibility takes the form of heat. Being evacuated towards the surroundings, this heat must been written dQirr < 0. In conditions of reversibility, he knows that dWadd = 0, so that no heat appears, no heat is evacuated, and dQrev = 0. Comparing both results, it effectively seems that the logical conclusion takes the form dQirr < dQrev suggested by Equation (11).
In a second time, the reader’s opinion may be slightly different because, while observing the use that is made of Equations (12) and (13) in thermodynamic calculations (see the numerical example given in Appendix 1), he discovers that the precise meaning of Equation (12) is:
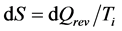 (14)
(14)
and that the precise meaning of Equation (13) is:
 (15)
(15)
The conclusion of this observation is that the term dQirr is not explicitly mentioned in Equations (14) and (15) and therefore its relation with dQrev is not accessible from a direct reading of these expressions. A complementary step is needed that consists in converting Equations (14) and (15), that have the dimension of entropy, in equations having the dimension of energy.
If we focus attention to the entropy Equation (15), which corresponds to the more general case, the conversion consists of multiplying each term by Te and the procedure leads to the energy equation:
 (16)
(16)
whose significance is:
 (17)
(17)
The term dSi being always positive (fundamental information associated to the second law) as the term Te (absolute temperature), the product TedSi is always positive.
Therefore, the terms dQirr and dQrev appear to be linked together by the relation:
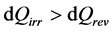 (18)
(18)
that can also be written:
 (19)
(19)
where dQadd has a positive value.
3. Consequences of These Observations on the Formulation of the First and Second Laws
Having in mind the relation dU = dQ + dW (Equation (3)), we immediately see that the proposals obtained in Section 2 are not compatible with the conventional understanding of the first law. If the term dQ really obeys the relation dQirr > dQrev (Equation (18)) and the term dW the relation dWirr > dWrev (Equation (9)), the term dU cannot obey the relation dUirr = dUrev (Equation (2)) but rather the relation:
dUirr > dUrev(20)
which appears as an extended interpretation of the first law.
A correlative observation can be made for the presentation of the second law in the sense that instead of using the entropy Equations (12) and (13) as a starting point of the reasoning, we can use as fundamental definitions of dQirr and dQrev the energy equations:
 (21)
(21)
 (22)
(22)
With these equations, the procedure used to define dQirr and dQrev becomes more homogeneous with the one used to define dWirr and dWrev (Equations (5) and (6)).
Correlatively, the conclusion TedS = dQrev + TedSi (Equation (16)), that has been indirectly derived from Equation (12) and (13), can be directly derived from Equation (21) and (22). Indeed, it can be observed from these expressions that the sign of the entropy variation dS is always that of dQ (as Te and Ti are absolute temperatures, they are positive). Knowing that dS has the same value in both equations (because S is a state function), the difference dQirr − dQrev takes the form:
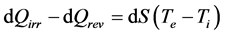 (23)
(23)
that is:
 (24)
(24)
With the condition Te > Ti leading to dQ > 0 and therefore to dS > 0 and the condition Te < Ti leading to dQ < 0 and dS < 0, we see that the product dS(Te – Ti) is always positive.
Consequently, the relation between the terms dQirr and dQrev can be written dQirr > dQrev or dQirr = dQrev + dQadd (with dQadd > 0) as it was already shown above by the use of the expressions (12) and (13) as starting definitions.
For a complete illustration of the analogy between both procedures, we have to show that the proposal dQirr = dQrev + dS(Te – Ti) given by Equation (24) and the proposal dQirr = dQrev + TedSi given by Equation (17) are really equivalent. In other words, we have to show that:
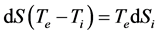 (25)
(25)
Knowing that dS = dSe + dSi, and therefore that dSi = dS – dSe, the right hand side of Equation (25) can be written TedS – TedSe. Similarly, the left hand side can be written TedS – TidS.
Eliminating TedS from both sides, the remaining terms are TedSe on one side and TidS on the other side, and we have to show that they are equal, i.e. that TedSe = TidS Concerning this question, it can be derived from Equation (14) that dQrev = TidS and from Equation (15) that . Thus, we effectively see that TedSe = TidS. This information is the sign that the choice of the energy Equations (21) and (22) to introduce the second law is really equivalent to the choice of the entropy Equations (12) and (13). The advantage of the energy Equations (21) and (22) is that they lead directly and without ambiguity to the proposal dQirr > dQrev, whose combination with the proposal dWirr > dWrev shows immediately that the inequality dUirr > dUrev seems to be a more adequate interpretation of the first law, than the usually admitted postulate dUirr = dUrev.
. Thus, we effectively see that TedSe = TidS. This information is the sign that the choice of the energy Equations (21) and (22) to introduce the second law is really equivalent to the choice of the entropy Equations (12) and (13). The advantage of the energy Equations (21) and (22) is that they lead directly and without ambiguity to the proposal dQirr > dQrev, whose combination with the proposal dWirr > dWrev shows immediately that the inequality dUirr > dUrev seems to be a more adequate interpretation of the first law, than the usually admitted postulate dUirr = dUrev.
As already done for the terms dW and dQ (Equation (10) and (19)) we can write Equation (20) under the form:
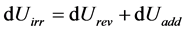 (26)
(26)
where dUadd is a positive term.
In conventional thermodynamics, because the equality dUirr = dUrev is admitted as a starting postulate, the term dUadd of Equation (26) has always a zero value and is not taken into account. Applied to an isolated system, this conception leads to the conclusion that dUsyst = 0, whatever the level of irreversibility of the processes occurring inside this system.
The conclusion is different if the term dUadd is taken into account. Let us imagine an isolated system composed of two parts, designated 1 and 2, that have a mutual exchange of energy. Applying Equation (26) to both parts, we get:
For part 1 
Fort part 2 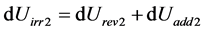
For the system 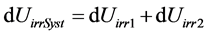
Knowing that dUrevSyst = 0 (because dUrev2 = –dUrev1), the result is:

i.e.: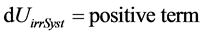 .
.
The information given by this last expression is that the internal energy of an isolated system increases if this system is the seat of internal exchanges of energy. Of course, because it opens a new prospect with regard to the classical conception, this conclusion raises the question of the physical origin of the additional energy designated dUadd.
4. A Possible Link between Thermodynamics and Relativity
To explain the creation of an additional energy within an isolated system, the reflexe spontaneously coming in mind is that we face a concrete illustration of the Einstein mass-energy relation E = mc2. Put forward in preliminary papers [5] [6] , this suggestion is a way to say that every irreversible process generates—inside the system to which it refers—an energy due to a correlative disintegration of matter. Although the change in mass is in most cases too small to be detectable, the corresponding increase in energy appears as a general feature, giving to the term dUadd the significance:
 (27)
(27)
and to Equation (26) the significance:
 (28)
(28)
In Equation (27) and (28) the minus sign placed in front of the term c2dm appears as a necessary condition to give dUadd a positive value. The procedure is the same as that used in Equation (3) to give dW a positive value when the system receives work (i.e. when the volume obeys the condition dV < 0) and a negative value when it provides work (i.e. when the volume obeys the condition dV > 0).
It is interesting to note that in some recent textbooks, [7] [8] , the need to connect thermodynamics with relativity is evoked.
From this point of view, Equation (28) can be looked as a preliminary attempt to present the first law, the second law and the Einstein mass-energy relation in a single formulation.
If we take into account the definitions concerning dW (Equations (4) and (5)) and those concerning dQ (Equations (21) and (22)) we are led to the idea that another possible writing of Equation (28) is:
 (29)
(29)
where  are the average values of Te, Ti, Pe and Pi during the process.
are the average values of Te, Ti, Pe and Pi during the process.
A detailed explanation of this formulation is given in Reference [6] .
5. What Are the Symptoms Revealing the Existence of the Additional Energy dUadd?
For the changes in energy designated under the symbols dW and dQ, the physical symptoms are well known. As implicitly written through the formulation dW = –PedV (Equation (3)), a variation of dW induces a change in the parameters P and V of the system. Similarly, the formulation dQ = TedS (Equation (21)), contains the implicit idea that a variation of dQ induces a change of the parameters T and S of the considered system.
Since all the terms P, T, V and S are state parameters of this system, their variations are the same, for a given process, whatever the level of irreversibility of the change in dW or in dQ.
In such conditions, what can be the symptoms of the energy variation noted dUadd in Equation (26) which represents, for a given change of state of a system, the difference between dUirr and dUrev?
In the context of everyday experiments (compression of a gas, heating of a liquid, etc), the change in mass is too small to be detectable, and therefore cannot give measurable information of the level of irreversibility of the process.
It seems that a possible answer may be searched for in the field of time and space. For a given process, by which the system passes from an initial state (P1, T1, V1, S1) to a final state (P2, T2, V2, S2), we easily conceive that the time required becomes shorter as the level of irreversibility is higher. Correlatively, it seems that the change in mass has a possible gravitational effect in the sense that the added contributions of different systems would lead to increase the distance between the celestial body in which they occur (the Earth in the present case) and the neighboring celestial bodies (the Moon particularly). Some preliminary comments about these topics can be found in references [9] [10] .
6. Extension of the Hypothesis to the Interpretation of Chemical Reactions
One of the advantages of the thermodynamic tool is that the sense of evolution of chemical reactions can be predicted by the sign of the change in free energy dG, knowing that G is defined by the relation:
![]() (30)
(30)
equivalent to:
![]() (31)
(31)
As explained in a previous paper ([6] § 2.1), the change in free energy dG, initially defined as:
![]() (32)
(32)
has the precise meaning:
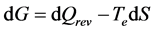 (33)
(33)
Confronted to Equations (16) and (17), this is equivalent to saying that:
 (34)
(34)
In a more general way (i.e. when we choose to define G as Equation (30), rather than Equation (31)), it can be shown that:
 (35)
(35)
Confronted to the relation  (Equation (28)), this is the sign that:
(Equation (28)), this is the sign that:
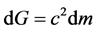 (36)
(36)
Knowing that chemical reactions imply a negative value of dG, it can be seen from Equation (36) that they are characterized by a decrease in mass.
Despite the fact that in ordinary chemical reactions, the change in mass is too small to be measurable, its consideration is important from the theoretical point of view. In the case of nuclear reactions, the change in mass is measurable but, referring to the usual understanding of the thermodynamic theory, a detectable change in mass is only possible in the context of an open system. This is probably the reason why numerical examples dealing with nuclear reactions are generally absent from thermodynamic textbooks. As shown in the discussion presented in Appendix 2 below, it seems that a change in mass occurs in every process, even when the system taken in consideration is defined as closed or isolated.
7. Is There a Thermodynamic Difference between Inert Systems and Living Systems?
The laws of thermodynamics were established on the basis of observations done on inert systems, i.e. systems made of inert matter, such as steam engines. Is it possible to apply them to living systems?
It is a matter of fact that the behavior of a living body is not the same after its death as it was before. Knowing that after its death, this behavior is the one corresponding to inert matter, that is to Equation (26) and (28), it is not evident to know if living matter obeys these equations.
The thermodynamic difference between living matter and inert matter has been studied for a long time by many scientists and has led to the concept of negentropy. Referring to Equation (13) or (15), i.e. to the conventional expression of the second law, it consists in the idea that a living system is characterized by a decrease in internal entropy (dSi < 0), instead of the usual increase (dSi > 0) that constitutes the characteristic of inert systems. Introduced by E. Schrödinger [11] in the middle of the 20th century, this concept is still a subject of active scientific discussion.
Examined under the light of Equations (16), (17) or (19), the problem remains the same, except that the condition dSi < 0 takes the form dUadd < 0, implying dm > 0. Similarly, the condition dSi > 0 takes the form dUadd > 0, implying dm < 0.
A few years ago, experiments were performed [12] showing a positive change in mass for a closed thermodynamic system made of a mixture of living and inert matter. In thermodynamics, it is well known that when a closed system is exclusively made of inert matter (a gas contained in a cylinder for example), its exchanges of energy with the surroundings never lead to a detectable change in mass. As a consequence, the reported observations were interesting from a double point of view: first because the change in mass was sufficient to be measurable, second because it was positive.
It seems that the results presented by this author have neither been confirmed nor contested. Taking into account the potential incidence of such information, it would probably be very interesting to perform new experiments.
Referring to Equation (28), a confirmation of the increase in mass would suggest that living matter is able to convert energy to matter, giving a negative value to the term dUadd of Equation (26). Such a behavior would contrast with inert matter behavior, which is supposed—in the present paper—to be characterized by the ability to convert matter to energy.
8. Further Considerations and Acknowledgments
Following the way opened by I. Prigogine , in the last decades of the 20th century, the thermodynamics of irreversible processes remains the object of active research. A selection of recent contributions is given in the References section, with approximate respect of their chronology. The papers mentioned were written by E. P. Gyftopoulos and G. P. Beretta , A. Bejan , A. Annila and U. Lucia . One of the major concepts analyzed is the Gouy-Stodola theorem, which establishes a relation between the lost available work and the entropy production.
Contratry to the above discussion that is eassily accessible to every scientist having some basis in macroscopic thermodynamics, the papers just mentioned are destined to readers highly specialized in physics.
Is there a link between both kinds of approach? Physicists are the best equipped to bring an answer and I express my thanks to those of them who will pay attention to the question.
9. Conclusions
The discussion presented in this paper is not a rejection of the thermodynamic theory but an extension and clarification. As already noticed, Equation (28) can be understood as a preliminary hypothesis suggesting a combination of the first and second laws with the Einstein mass-energy relation.
Because the thermodynamic theory has been stated at a time when relativity was not known, we easily conceive that it was impossible, for its creators, to imagine this link with the mass-energy relation.
The advantage of taking it into account is that thermodynamics seems much easier to learn and to teach and that processes occurring with a measurable change in mass, such as nuclear reactions, can enter within the framework of the theory.
If the hypothesis advanced in this paper is recognized as valid, it will be the sign that far from being reserved to exceptional phenomena, the concept of relativity is of general use and appears as a necessary component for the thermodynamic understanding of everyday processes.
References
- Nordstrom, D.K. and Munoz, J.L. (1986) Geochemical Thermodynamics. Blackwell Scientific Publications.
- Anderson, G.M. and Crerar, D.A. (1993) Thermodynamics in Geochemistry. Oxford University Press, Oxford.
- Reiss, H. (1965). Methods of Thermodynamics. Blaisdell Publishing Company, New York.
- Abbott, M.M. and Van Ness, H.C. (1976) Theory and Problems of Thermodynamics. Shaum’s Outline Series. McGraw-Hill, New York.
- Tane, J.-L. (2000) Evidence for a Close Link between the Laws of Thermodynamics and the Einstein Mass-Energy Relation. Journal of Theoretics, Vol. 2, No. 3. http://www.journaloftheoretics.com/Articles/aArchive.htm
- Tane, J.-L. (2010) Unless Connected to Relativity, the First and Second Laws of Thermodynamics are Incompatible. http://arxiv.org/abs/0910.0781 and The General Science Journal http://gsjournal.net/
- Kondepudi, D. (2008) Introduction to Modern Thermodynamics. Wiley, Hoboken (See pp. 79-80 The Comment on the Thermodynamic Interpretation of Nuclear Reactions).
- Linder, B. (2011) Elementary Physical Chemistry. World Scientific, Singapore City (See p. 15, The Wish to Insert the Mass-Energy Relation in the First Law).
- Tane, J.-L. (2011) A Possible Link between Time and Mass. The General Science Journal.
- Tane, J.-L. (2008) Possible Impact in Astronomy of the Link between Thermodynamics and Relativity. The General Science Journal.
- Schrödinger, E. (1944) What Is Life? Cambridge University Press, Cambridge (Reprinted in 1992, with a Foreword by Roger Penrose).
- Sorli, A. The Additional Mass of Life. Journal of Theoretics, Vol. 4, No. 2.
- Prigogine, I. (1967) Introduction to Thermodynamics of Irreversible Processes. 3rd Edition, John Wiley & Sons, Hoboken.
- Gyftopoulos, E.P. and Beretta, G.P. (2005) Thermodynamics. Foundations and Applications. Dover Publications, Mineola.
- Bejan, A. (2006) Advanced Engineering Thermodynamics. John Wiley, Hoboken.
- Annila, A. (2010) The 2nd Law of Thermodynamics Delineates Dispersal of Energy. International Review of Physics, 4, 29-34.
- Lucia, U. (2012) Gouy-Stodola Theorem as a Variational Principle for Open Systems. http://arxiv.org/abs/1208.0177
- Lucia, U. (2013) Stationary Open Systems: A Brief Review on Contemporary Theories on Irreversibility. Physica A, 392, 1051-1062. http://dx.doi.org/10.1016/j.physa.2012.11.027
Appendix 1
The numerical example chosen here is destined to illustrate the fact that when Equations (12) and (13) are used in a thermodynamic calculation, the value given to the term dQ is the same in both cases and corresponds to dQrev. This example is extracted from a thermodynamics course and the problem consists in calculating the change in entropy (ΔS, ΔSe and ΔSi) of 1 liter of water (1000 g) that is heated from 20˚C (293 K) to 100˚C (373 K), by contact with a thermostat at 100˚C (373 K). Some complementary comments, generally absent from textbooks, are added. They concern the thermodynamic interest of the term designated T* which represents the average value of the temperature (![]() or
or![]() ) during the heating process.
) during the heating process.
Knowing that cpwater = 4.18 J·g–1 and admitting that it can be considered constant over the interval of temperature, the answer is detailed as follows:
 (A)
(A)
![]() (B)
(B)
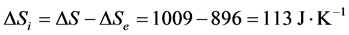 (C)
(C)
If we compare these equations with those encountered in Section 2, we can note the following correspondences:
In Equation (B), the term ![]() represents ΔQrev, that is the integration of the term dQrev of Equation (21) and (22). The detailed expression is:
represents ΔQrev, that is the integration of the term dQrev of Equation (21) and (22). The detailed expression is:
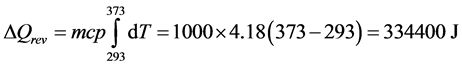
In Equation (A), the term  can also be noted:
can also be noted:
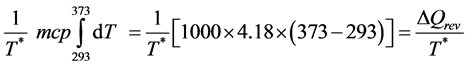
where T* is the average temperature T during the heating process. Knowing that in conditions of reversibility, we have always Te = Ti, the symbol T* represents indifferently ![]() and
and![]() .
.
Having ΔS = 1009 J·K–1 and ΔQrev = 334,400 J, the value of T* is:

As already noticed in Section 2, the term ΔQirr is not directly visible in these equations, but using the results just obtained and integrating Equation (16) and (17) (or Equation (21) and (22)), we get respectively:
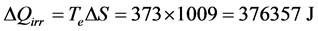
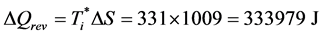
The slight difference (0.12%) between this last result (333,979 J) and the one previously found for ΔQrev (334,400 J) comes from the fact that the indication T* = 331 K is a rounded value.
Then using Equation (19), the term ΔQadd can be calculated by difference. Its value is:

It can be seen through these results that we have really ΔQirr > ΔQrev and that the positive difference ΔQadd represents an additional energy that is created inside the system, due to the irreversibility of the heating process (Te ≠ Ti). As suggested in Section 5 and Reference [10] , it is possible that this energy be gravitational.
Appendix 2
The question examined here concerns the thermodynamic interpretation of the process of gas expansion into vacuum. Let us consider an isolated system having the form of a horizontal cylinder divided in two parts separated by a mobile frictionless piston. In the initial state, Part 1 contains a gas while Part 2 has been evacuated. If the piston, initially locked, is liberated, it will move towards the vacuum, until the volume of this last one becomes zero.
In the usual interpretation of the process, attention is exclusively focused on the gas, and the vacuum is generally not taken into account. Therefore, the discussion only concerns part 1 and can be summarized as follows:
 (because
(because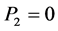 )
)
dQ1 = 0 (because we don’t conceive that the gas can exchange heat with the vacuum);
dU1 = 0 (being the sum dW1 + dQ1);
 (because this expression refers to dU1rev, which is supposed to obey the relation dU1irr = dU1rev according to the usual understanding of the first law);
(because this expression refers to dU1rev, which is supposed to obey the relation dU1irr = dU1rev according to the usual understanding of the first law);
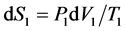 , which is positive, since all the terms P1, dV1 and T1 are positive.
, which is positive, since all the terms P1, dV1 and T1 are positive.
The process is therefore interpreted as an increase in entropy of the gas, while its internal energy remains constant.
In the alternative interpretation of the process, both parts 1 and 2 are taken into account and the results obtained take the form:
 (because P2 = 0);
(because P2 = 0);
 (because dV2 = –dV1); therefore dW2 is positive dQ1 = 0 and dQ2 = 0 (because the gas cannot exchange heat with the vacuum);
(because dV2 = –dV1); therefore dW2 is positive dQ1 = 0 and dQ2 = 0 (because the gas cannot exchange heat with the vacuum);
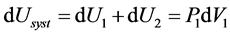 , whose value is positive as already seen.
, whose value is positive as already seen.
Therefore, the global system is concerned by an increase in internal energy. Since this system has been defined as isolated, this increase in energy seems to be linked to an internal disintegration of matter, according to Equation (28).
Knowing that Part 2 (the vacuum) has totally disappeared at the end of the process, we can imagine that this increase in energy concerns Part 1 (the gas). Dividing its numerical value (P1dV1) by T1, we get the increase in entropy P1dV1/T1 already obtained, but we are now aware of its relation with an increase in energy, information that is omitted in the classical interpretation. Because S is a state function, dS is independent of the level of irreversibility of the process. It is not the case of U and dU.

