Engineering
Vol.07 No.05(2015), Article ID:56603,10 pages
10.4236/eng.2015.75023
Theoretical Research on R245fa Condensation Heat Transfer inside a Horizontal Tube
Shengchun Liu*, Yan Huo, Zhaowei Liu, Lan Li, Jinghong Ning
Tianjin Key Laboratory of Refrigeration technology, Tianjin University of Commerce, Tainjin, China
Email: *liushch@tjcu.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 April 2015; accepted 22 May 2015; published 25 May 2015
ABSTRACT
Numerical simulation on R245fa condensation inside an inner diameter of 8 mm horizontal tube is researched in this paper. The effect of variation in velocity, condensation temperature and superheat of inlet steam and variation in cooling water temperature on heat transfer coefficient are investigated as a parametric study. Condensation process of steam has been successfully modeled by applying a user defined function (UDF) added to the commercial computational fluid dynamics (CFD) package. By analyzing the corresponding condensate contours and the curves of local heat transfer coefficient, the relationships between condensation heat transfer coefficient and various parameters of R245fa inside horizontal tube are obtained. It shows that the heat transfer coefficient increases by the increase in velocity, condensation temperature and superheat of inlet steam and the decrease in cooling water temperature. The errors between the heat transfer coefficient of simulation result and model of Wang and Shah are within ±30%. The parametric study will provide the basis for designing efficient heat exchangers of R245fa.
Keywords:
Condensation Heat Transfer, R245fa, Numerical Simulation, Horizontal Tube

1. Introduction
Under the dual pressures of energy and environmental issues, developing environmentally friendly refrigerant becomes one of the three major issues facing the refrigeration and air conditioning industry. In recent years, R245fa is an environmentally friendly substituted refrigerant, which is researched by international experts. It has characteristics of excellent thermal resistance, low toxicity, no chlorine, and no damaging effects on the ozone layer. And comparing with R134a, it has a lower pressure level [1] . It is more stable used in some specific situations. As a working fluid of high critical temperature among the zero ODP refrigerants, R245fa represents a substitute for R123 and R11 used in high temperature heat pumps, in jet-pump refrigerators, in centrifugal chillers and in heat recovery power cycles [2] . And R245fa shows high power-generating ability and high economical efficiency in the low-temperature range [3] . R245fa as working fluid in the low-temperature solar power rankine cycle system is feasible and the performance is acceptable [4] . Eames’s experiment [5] results demonstrate that low-grade heat can be used to drive efficient jet-pump refrigeration systems, using R245fa as their working fluid, for high temperature applications, such as air conditioning.
It is very important to research the heat transfer characteristics of refrigerants R245fa. Zou et al. [6] used R245fa, R134a, R410A, and R32 to explore the effects of fluid properties on refrigerant distribution in the vertical header of a reversible micro-channel heat exchanger. By comparing the results of experiments, R245fa was found to the best distribution. It is because of the low steam density and high liquid density of R245fa. Many scholars have studied the flow boiling heat transfer of R245fa. In Vakili-Farahani et al.’s experiment [7] with refrigerants R1234ze and R245fa, the heat transfer coefficient increases with rising of saturated temperature, heat flux and mass flux. Tibiriçá et al. [8] did experiment in a horizontal 2.3 mm I.D. stainless steel tube utilizing working fluids R134a and R245fa. It was concluded that the heat transfer coefficient was related to heat flux, mass velocity and quality. Ong et al. [9] , Pike-Wilson et al. [10] and Agostini et al. [11] researched on the flow boiling patterns, pressure drop and heat transfer characteristic of R245fa in a tube. Researching on condensation heat transfer inside tubes is another important aspect of heat transfer characteristics, and the literature on condensation of R245fa is few.
In this paper, condensation heat transfer is simulated by using the commercial software CFD, VOF model and UDF (User-Defined Functions). Numerical simulation on R245fa steam condensing in the inner diameter of 8 mm horizontal tube and analysis is conducted in terms of steam flow rate, cooling water temperature, condensation temperature and superheat. By analyzing the corresponding condensate contours and the curves of local heat transfer coefficient, the relationships between condensation heat transfer coefficient and various parameters inside horizontal tube are obtained. It can provide the basis for designing efficient heat exchangers of R245fa.
2. Numerical Methodology
A horizontal tube with inner diameter of 8 mm, length 500 mm is considered. And the model coordinates is shown in Figure 1. The origin of the coordinate system is at the center of the interface, the pipe longitudinal direction of the X-axis, the vertical direction for the Z-axis, the influence of gravity is considered in the simulation, and the acceleration of gravity is 9.806 N/kg, the Z-axis is parallel to direction of gravity.
According to pipe geometry, the model is meshed by size of 1 mm using ring hexahedral structured grid. The refrigerant flows into the pipe, and condensation occurs when it comes across the colder wall surface.
The condensation film attached to the wall, and the vapor is in the central area of pipe. Considering the impact of the boundary layer near the wall, Boundary layer near the wall is meshed, and the initial boundary layer mesh size is 0.2 mm, growth ratio of 1.2, the boundary layer mesh layers of 6. The meshing results are shown in Figure 2 and Figure 3.
Figure 4 is a simplified schematic diagram of the simulated section of the tube and boundary conditions, Inlet and outlet boundary condition are set to velocity-inlet and outflow respectively. And constant temperature of the pipe wall is also set.
Many researchers apply VOF model to go on investigation of two phase flow. Such as literature [12] -[14] using it to study boiling and literature [15] [16] using it to research condensation. In this paper, using commercial software Fluent 14.0, multiphase flow model chooses VOF model, calculating as follows within controlling cell.
Within each cell, the volume fraction of phases is 1 for gas-liquid two-phase flow, and as the presence of the following formula:
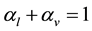 (1)
(1)
Density ρ within each cell, the thermal conductivity λ, the dynamic viscosity μ and thermodynamic energy E are calculated as follows:
Figure 1. The model coordinates.
Figure 2. The sectional grid.
Figure 3. The grid of wall surface.
Figure 4. Simplified schematic diagram and boundary conditions.
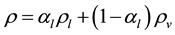 (2)
(2)
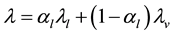 (3)
(3)
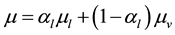 (4)
(4)
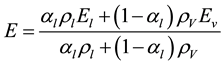 (5)
(5)
And continuity equation, momentum equation and energy equation can be expressed as follows:
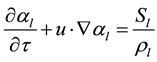 (6)
(6)
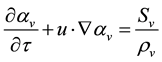 (7)
(7)
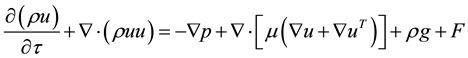 (8)
(8)
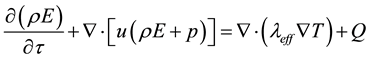 (9)
(9)
In the present CFD model, the liquid evaporation and vapor condensation effects can be considered by incorporating mass and energy sources into the continuity and energy equations, respectively. The source term for the energy equation can be obtained by multiplying the rate of mass transfer by the latent heat. In a CFD simulation, the source terms act on the whole fluid domain, so the phase change effect both at liquid surface and in the bulk region can be considered simultaneously. All of the source terms are driven by the cell temperature, T, and implemented via customized UDF. Based on the following temperature regimes, the mass transfer can be described as follows [17] :
If 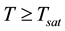 (evaporation),
(evaporation),
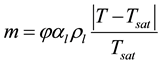 (10)
(10)
If 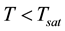 (condensation),
(condensation),

Using the k-ε turbulence model, the formats of simulation variables to select are shown in Table 1, and the convergence criterion of control equations are shown in Table 2.
3. Results and Discussion
Refrigerants R245fa inlet steam is saturated, the condensation temperature is 314 K, the wall temperature is 293 K, and the inlet steam flow rate is 6 m/s, 10 m/s, 14 m/s and 18 m/s respectively. The changes of film thickness of the inner tube and heat transfer coefficient are shown in Figure 5.
From above curves, it is concluded that the local heat transfer coefficient increased, the thickness of condensate film decreased and the rate of increase of condensation film thickness slow down, as the inlet steam flow
Table 1. Format of variables.
Table 2. The convergence criterion of control equations.
Figure 5. Curves under different flow rates.
rate increases. And condensation heat transfer coefficient changes dramatically, when refrigerant steam flows into tube. At the Steam flow rate of 6 m/s, condensate begins to increase rapidly in 0.3 m at growth gradually accelerated. As the flow rate increases, the changing rate of local heat transfer coefficient increases. The faster steam flow rate, the stronger the shear is, the more slowly the condensation film thickness increases.
The inlet velocity is 10 m/s, and the contours of liquid volume fraction are shown in Figure 6 and Figure 7, respectively. The surface heat transfer coefficient is shown in Figure 8. The surface heat transfer coefficient increases at first and then decreases, therefore there is a maximum, and the rate of increase becomes faster close to the entrance of steam. It can be interpret as part of the steam condensed to form droplets at the inlet; with the process of condensation, droplets become larger, increasing the heat transfer area. Then the droplets become liquid film, film formation increases heat resistance, making the heat transfer coefficient decreases.
As shown in Figure 7 and Figure 8, because the steam temperature is higher than that of pipe wall, the steam condenses on the wall. With the working fluid flowing and the occurrence of condensation, the film thickness increased along direction of flowing. Due to gravity, most of liquid accumulates in the bottom of the pipe. The condensation heat transfer coefficient changed dramatically as refrigerant steam flowed into tube. Then, the heat transfer coefficient reduced, the heat transfer coefficient is further reduced quickly at the position of about 0.3 m.
Refrigerants R245fa inlet steam is saturated, the inlet steam flow rate is 10 m/s, the condensation temperature is 314 K, and the wall temperature was 288 K, 291 K, 293 K and 295 K respectively. The changes of film thickness of the inner tube and heat transfer coefficient are shown in Figure 9. The lower the temperature of the tube wall, the great heat transfer coefficient is, the more condensed liquid is. Analysis of the causes is that the lower tube wall temperature, the greater heat temperature difference, and the larger condensation heat transfer. Condensate begins to increase rapidly at 0.3 m and the thickening rate of film increased, heat transfer coefficient decreases rapidly.
Refrigerants R245fa inlet steam is saturated, the inlet steam flow rate is 10 m/s, the wall temperature is 293 K, and the condensation temperature is 308 K, 313 K and 318 K, respectively. The changes of film thickness of the inner tube and heat transfer coefficient are shown in Figure 10.
Changes of the film thickness and heat transfer coefficient along tube are similar to the cooling water temperature trends under condensation temperatures. The larger the heat transfer coefficient, the thicker the condensation film. The rate of condensation film changing become fast with the rising of condensation temperature. These can be expressed as the higher condensation temperature, the greater the temperature difference, there is a growing rate of condensation. That condensate begins to increase rapidly at 0.3 m and the rate of increase gradually accelerated can also be obtained.
Refrigerants R245fa inlet steam is superheated with 1 K, 5 K, 10 K and 15 K. The inlet steam flow rate is 10 m/s, the wall temperature is 293 K, and the condensation temperature is 314 K, respectively. The changes of film thickness and heat transfer coefficient are shown in Figure 11.
When the superheat increases, the heat transfer coefficient becomes larger and the amount of condensate reduces. Superheat temperature difference leads to heat transfer coefficient increasing, but the amount needed for




Figure 6. The contours of liquid volume fraction at different positions.
Figure 7. The contours of liquid volume fraction along the tube at the velocity of 10 m/s.
Figure 8. The surface heat transfer coefficient along the tube at the velocity of 10 m/s.
Figure 9. Curves under different wall temperature.
Figure 10. Curves under different condensation temperature.
Figure 11. Curves under different superheat.
the cold steam condensation increases. Film thickness starts to increase rapidly at 0.3 m, the growth rate increases gradually, and the curve of corresponding heat transfer coefficient has the tendency to decline rapidly.
As the inlet steam flow rateis 10 m/s, the wall temperature is 293 K, and condensation temperature is 308 K, the errors between the heat transfer coefficient of simulation result and model of Wang [18] and Shah [19] are within ±30%.
4. Conclusions
By simulation on the process of R245fa condensing inside a horizontal tube and analysis of simulation results, various parameters have great influences on the condensation heat transfer coefficient. The simulation results show that when the inner diameter of tube is 8 mm, the heat transfer coefficient and film thickness have significant changes after the position of 0.3 m. Considering the changes of film thickness and heat transfer coefficient under different conditions, some relevant measures can be taken to reduce the film thickness at about 0.4 m and to enhance heat transfer in this case. The changing regulars of film thickness and heat transfer coefficient in different diameter can be got by using the similar method of simulation in the paper. Then, the position can be obtained to enhance heat transfer. And it can provide the basis for designing efficient heat exchangers of R245fa.
By comparing the different factors on the condensation heat transfer, it can be seen that the ways of influences of cooling water temperature, condensing temperature and steam flow rate on the condensation heat transfer are different. The increasing of team flow rate results in enhanced shear, and condensation film is not stable in the presence of the tube, so film thickness reduces, and heat transfer coefficient increases. The wall temperature decreases or condensing temperature rises, and the temperature difference increases, so that the heat transfer coefficient increases. The heat transfer coefficient of simulation results is close to the model of Wang and Shah. Thus, the model and method of simulation are suitable for process of condensation.
Acknowledgements
This research was supported by The Ministry of Science and Technology of the People’s Republic of China, (863 Program) (Grant No. 2012AA053001).
References
- Wang, X.D., Zhao, L. and Wang, J.L. (2000) Experimental Investigation on the Low-Temperature Solar Rankine Cycle System Using R245fa. Energy Conversion and Management, 52, 946-952. http://dx.doi.org/10.1016/j.enconman.2010.08.022
- Angelino, G. and Invernizzi, C. (2003) Experimental Investigation on the Thermal Stability of Some New Zero ODP Refrigerants. International Journal of Refrigeration, 26, 51-58. http://dx.doi.org/10.1016/S0140-7007(02)00023-3
- Saleh, B., Koglbauer, G., Wendland, M. and Fischer, J. (2007) Working Fluids for Low-Temperature Organic Rankine Cycles. Energy, 32, 1210-1221. http://dx.doi.org/10.1016/j.energy.2006.07.001
- Wang, X.D., Zhao, L., Wang, J.L., Zhang, W.Z., Zhao, X.Z. and Wu, W. (2010) Performance Evaluation of a Low- Temperature Solar Rankine Cycle System Utilizing R245fa. Solar Energy, 84, 353-364. http://dx.doi.org/10.1016/j.solener.2009.11.004
- Eames, I.W., Ablwaifa, A.E. and Petrenko, V. (2007) Results of an Experimental Study of an Advanced Jet-Pump Refrigerator Operating with R245fa. Applied Thermal Engineering, 27, 2833-2840. http://dx.doi.org/10.1016/j.applthermaleng.2006.12.009
- Zou, Y. and Hrnjak, P.S. (2014) Effects of Fluid Properties on Two-Phase Flow and Refrigerant Distribution in the Vertical Header of a Reversible Microchannel Heat Exchanger―Comparing R245fa, R134a, R410A, and R32. Applied Thermal Engineering, 70, 966-976. http://dx.doi.org/10.1016/j.applthermaleng.2014.06.021
- Vakili-Farahani, F., Agostini, B. and Thome, J.R. (2013) Experimental Study on Flow Boiling Heat Transfer of Multiport Tubes with R245fa and R1234ze(E). International Journal of Refrigeration, 36, 335-352. http://dx.doi.org/10.1016/j.ijrefrig.2012.12.007
- Tibiriçá, C.B. and Ribatski, G. (2010) Flow Boiling Heat Transfer of R134a and R245fa in a 2.3 mm Tube. International Journal of Heat and Mass Transfer, 53, 2459-2468. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2010.01.038
- Ong, C.L. and Thome, J.R. (2009) Flow Boiling Heat Transfer of R134a, R236fa and R245fa in a Horizontal 1.030 mm Circular Channel. Experimental Thermal and Fluid Science, 33, 651-663. http://dx.doi.org/10.1016/j.expthermflusci.2009.01.002
- Pike-Wilson, E.A. and Karayiannis, T.G. (2014) Flow Boiling of R245fa in 1.1 mm Diameter Stainless Steel, Brass and Copper Tubes. Experimental Thermal and Fluid Science, 59, 166-183. http://dx.doi.org/10.1016/j.expthermflusci.2014.02.024
- Agostini, B., Thome, J.R., Fabbri, M., Michel, B., Calmi, D. and Kloter, U. (2008) High Heat Flux Flow Boiling in Silicon Multi-Microchannels―Part II: Heat Transfer Characteristics of Refrigerant R245fa. International Journal of Heat and Mass Transfer, 51, 5415-5425. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2008.03.007
- Rabha, S.S. and Buwa, V.V. (2009) Volume-of-Fluid (VOF) Simulations of Rise of Single/Multiple Bubbles in Sheared Liquids. Chemical Engineering Science, 65, 527-537. http://dx.doi.org/10.1016/j.ces.2009.06.061
- Yang, Z., Peng, X.F. and Ye, P. (2008) Numerical and Experimental Investigation of Two Phase Flow during Boiling in a Coiled Tube. International Journal of Heat and Mass Transfer, 51, 1003-1016. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2007.05.025
- Huang, M., Yang, Z., Duan, Y.Y. and Lee, D.J. (2011) Bubble Growth for Boiling Bubbly Flow for R141b in a Serpentine Tube. Journal of the Taiwan Institute of Chemical Engineers, 42, 727-734. http://dx.doi.org/10.1016/j.jtice.2011.02.007
- Chen, S.H., Yang, Z., Duan, Y.Y., Chen, Y. and Wu, D. (2014) Simulation of Condensation Flow in a Rectangular Microchannel. Chemical Engineering and Processing, 76, 60-69. http://dx.doi.org/10.1016/j.cep.2013.12.004
- Da Riva, E. and Del Col, D. (2012) Numerical Simulation of Laminar Liquid Film Condensation in a Horizontal Circular Minichannel. Journal of Heat Transfer, 134, Article ID: 051019. http://dx.doi.org/10.1115/1.4005710
- Wang, L., Li, Y.Z., Li, C. and Zhao, Z.X. (2013) CFD Investigation of Thermal and Pressurization Performance in LH2 Tank during Discharge. Cryogenics, 57, 63-73. http://dx.doi.org/10.1016/j.cryogenics.2013.05.005
- Wang, W.W.W., Radcliff, T.D. and Christensen, R.N. (2002) A Condensation Heat Transfer Correlation for Millimeter-Scale Tubing with Flow Regime Transition. Experimental Thermal and Fluid Science, 26, 473-485. http://dx.doi.org/10.1016/S0894-1777(02)00162-0
- Shah, M.M. (2010) Heat Transfer during Condensation inside Small Channels: Applicability of General Correlation for Macrochannels. Proceedings of the 14th International Heat Transfer Conference, Washington DC, 8-13 August 2010, 298-303.
Nomenclature
I.D. [mm] Inner diameter
P [pa] Pressure
T [K] Temperature
x [m] Cartesian axis direction
y [m] Cartesian axis direction
z [m] Cartesian axis direction
u [m/s] Radial velocity
v [m/s] Axial velocity
[s] Time
m [kg] Mass transfer at the surface
E [J] Thermodynamic energy
d [mm] Diameter
h [w/(m2∙k)] Heat transfer coefficient
Special Characters
g [N/kg] The acceleration of gravity
α [-] Liquid mass fraction
φ [1/s] Time relaxation parameter
ρ [kg/m3] Density
μ [kg/m∙s] Viscosity
λ [w/(m∙k)] Thermal conductivity
Subscripts
l Liquid phase
v Vapor phase
sat Saturation
eff Effective
NOTES
*Corresponding author.

















