Engineering
Vol.06 No.13(2014), Article ID:52325,12 pages
10.4236/eng.2014.613084
Investigation of the Flow Pattern inside a Diesel Engine Injection Nozzle to Determine the Relationship between Various Flow Parameters and the Occurrence of Cavitation
Hagar Alm-Eldin Bastawissi, Medhat Elkelawy
Department of Mechanical Power Engineering, Tanta University, Tanta, Egypt
Email: medhatelkelawy@f-eng.tanta.edu.eg
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 October 2014; revised 17 November 2014; accepted 2 December 2014
ABSTRACT
In diesel engines the fuel injection system produces the spray, which directly affects the combustion of the fuel, which in turn determines the production of pollutants. In spite of this, the details of this causal relationship remain unclear. There is, however, a lack of quantitative experimental data for determining and visualizing the cavitation inside real size diesel injector nozzle. The present work is devoted to analyze analytically the flow pattern inside the nozzle of a diesel engine working with hydrocarbon fuel (Diesel fuel) and to predict the relationship between the various flow parameters and occurrence of fuel cavitation in such nozzles. Basic physical parameters affecting this phenomenon are identified and quantified while the effect of nozzle geometry, fuel injection pressure, and engine cylinder temperature upon the flow pattern and occurrence of cavitation in such nozzles are assessed. In this study, a commercial computational fluid dynamics (CFD) package (FLUENT-T grid) is used while a computational grid is generated for the real geometry of diesel injector nozzle using (ANSYS). The suitability of the generated computational grid to give reliable results is examined using the suitable procedures and techniques. The results indicated that, cavitation modeling has reached a stage of maturity and it can usefully identify many of the cavitation structures present in internal nozzle flows and their dependence on nozzle design and flow conditions. The qualitative distributions and comparison of cavitation inception and distribution as well as flow parameters at the nozzle exit are also studied.
Keywords:
Diesel Injector Nozzle, Computational Fluid Dynamic (CFD), Cavitation

1. Introduction
In order to understand the whole breakup process of the diesel spray, it is necessary to determine the phenomena which lead to primary and secondary breakup caused by interaction with the dense gas phase and collision with other liquid elements. The knowledge of the spray forming phenomena is essential to allow predictions of the spray behavior and the mixture preparation during the injection process. To reach future emission standards, the fuel distribution in the combustion chamber and the droplet size distribution must be controlled appropriately. The different approaches to enhance the diesel fuel spray and reduce the diesel engine emissions while engine performance and soot formation remain almost constant have been used [1] - [3] . In which, the use of fuel additive to enhance the fuel mixture where a low boiling point fuel such as CO2, gas fuel, or gasoline is mixed with a higher boiling point fuel such as diesel gas oil. So, the mixed fuel is particularly has the potential to achieve fast evaporation and relatively lean and homogeneous mixtures. The combination of the multiple fuel injection strategy with the Exhaust Gas Recirculation technique is studied as well [4] . The results from this study have demonstrated that the use of the multiple fuel injection strategy can effectively reduce the NOx emission from diesel engines.
CFD calculations of the internal nozzle flow have shown that cavitation strings are formed in the areas where large structures [5] [6] . The injection rate is directly affected by the cavitation and the injection nozzle will be choked when this phenomenon appears. Thus, the measurement of the momentum flux can be combined with the injection rate to derive the velocity at the nozzle exit [7] [8] . Also, the influence of nozzle geometry on the internal flow characteristics of a diesel injector has been carried out with a simulation analysis [9] - [12] . The simulation studies confirm the tendency observed in experiments, that the nozzle geometry significantly influences the inner flow characteristics. In particular, by increasing the hydro-grinding radius of the orifice inlet, the mean outlet velocity near the wall and the discharge coefficient are increased, while the zone of cavitating flow is reduced. The experimental studies of the effect of various injection parameters on macro characteristics of diesel sprays generated by a state of the art common-rail injection system have been reported [13] - [15] . Cavitation on the macroscopic spray behavior point of view leads to an increment of the spray cone angle. On the other hand, from the point of view of the internal flow, the nozzle outlet velocity increases when cavitation appears. This phenomenon can be explained by the reduction in the cross section of the liquid phase in the outlet section of the nozzle hole.
The study of the nozzle internal flow and the cavitation in real size injectors is challenging, both theoretically and experimentally. In order to obtain the atomization characteristics due to the cavitation in the nozzle flow, the visualization of the cavitation need to perform by the flow visualization system, and atomization characteristics such as Sauter mean diameter (SMD) and droplet mean velocity is determined by using a particle analyzer system [16] - [18] . The pictures of the light sheet experiment taken with a CCD camera were compared with photographs taken by the shadowgraph technique under the same injection conditions [19] - [21] . As a result the cavitation films could be observed as thin objects which do not extend into the internal flow of the injection nozzle. In addition, even under higher injection pressures, no accumulation or foam of bubbles could be noticed in the spray nozzle hole. This leads to the conclusion that there is an intact liquid core, leaving the nozzle even at high injection pressures. The flow in nozzles of different sizes is also studied by using transparent nozzles of the same size as in diesel injectors and refractive index matching. In a steady flow rig, short exposure video pictures of the flow were made at injection pressure up to 100 MPa [22] .
Since the associated two-phase flow field is turbulent and characterized by large pressure gradients with injection duration in order of a few milliseconds. Also, the fluid flows through the holes at very high speeds, on the order of hundred meters per second. Furthermore, the nozzles are typically about a millimeter long and a fraction of a millimeter in diameter. For that aim, herein we report a computational investigation of the internal nozzle flow and cavitation characteristics in a real size diesel injector.
The present study is based on previous authors’ work in which we introduced a new criteria to identify many of the characteristics and strength of cavitation on nozzle performance, and so significantly contribute to nozzle design and optimization of cavitation production inside diesel injector nozzle [23] . The cavitation simulation model implemented, as well as the suitable turbulence model used in this study is extensively studied and examined quantitavely in authors’ work [24] . That makes the present study results unrevealing the properties of the internal flow patterns of a diesel injection nozzle and in particular the cavitation inside the injector nozzle with high accuracy and dependency.
This study highlights the importance of cavitation modeling to identify many of the vapor structures that exist in internal nozzle flows, and can ascertain their dependence on both nozzle design and flow conditions. The present numerical study aims at furthering of the cavitation processes that occurs inside diesel injector, especially under high-pressure injection conditions. We believe that in the parametric present study it is the first time to introduce the originality of cavitation phenomenon inside the real size diesel injector nozzle effectively under realistic injection pressures and nozzle geometry as well as the system temperature.
2. Mathematics and Numerical Method Descriptions
The basic equations and physical models applied to a single phase flow, which are the continuity and momentum equations, and the turbulence modeling equations. The equation for conservation of mass or continuity equation is the general form of the mass conservation equation and is valid for incompressible as well as compressible flows which described by Equation (1)
 (1)
(1)
The source term in the right hand side 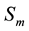 is the mass added to the continuous phase from the dispersed second phase (e.g., due to vaporization of liquid droplets) and any user-defined sources. The applied equation for conservation of momentum in an inertial (non-accelerating) reference frame is described by Equation (2):
is the mass added to the continuous phase from the dispersed second phase (e.g., due to vaporization of liquid droplets) and any user-defined sources. The applied equation for conservation of momentum in an inertial (non-accelerating) reference frame is described by Equation (2):
 (2)
(2)
where 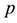 is the static pressure,
is the static pressure, 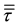 is the stress tensor, and
is the stress tensor, and 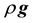 and
and  are the gravitational body force and external body forces (e.g., that arise from interaction with the dispersed phase), respectively. The stress tensor
are the gravitational body force and external body forces (e.g., that arise from interaction with the dispersed phase), respectively. The stress tensor  is given by Equation (3):
is given by Equation (3):
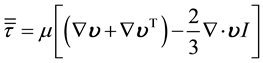 (3)
(3)
where 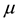 is the molecular viscosity,
is the molecular viscosity, 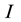 is the unit tensor. The turbulence model used in the simulation was the renormalization-group (RNG) k-ε model which was derived using a rigorous statistical technique. The RNG k-ε model is similar in form to the standard k-ε, but includes some refinements which made it more suitable to be employed in our simulation analysis. Those modifications enhance the accuracy of swirling and rapidly strained flows [25] .
is the unit tensor. The turbulence model used in the simulation was the renormalization-group (RNG) k-ε model which was derived using a rigorous statistical technique. The RNG k-ε model is similar in form to the standard k-ε, but includes some refinements which made it more suitable to be employed in our simulation analysis. Those modifications enhance the accuracy of swirling and rapidly strained flows [25] .
The cavitation model implemented is based on the so-called “full cavitation model”, developed by Singhal et al. [23] [25] [26] . In the standard two-phase cavitation model, the model assumes that the system under investigation involves only two phases (a liquid and its vapor), and a certain fraction of separately modeled noncondensable gases whose mass fraction is known in advance. Also, both bubble formation (evaporation) and collapse (condensation) are taken into account in the model. Standard governing equations in the mixture model and the mixture turbulence model describe the flow and account for the effects of turbulence. A vapor transport equation governs the vapor mass fraction, 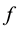 , given by Equation (4):
, given by Equation (4):
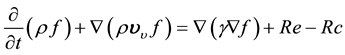 (4)
(4)
where,  is the mixture density,
is the mixture density,  is the velocity vector of the vapor phase,
is the velocity vector of the vapor phase, 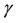 is the effective exchange co- efficient, and
is the effective exchange co- efficient, and 

Significant effect of turbulence on cavitating flows has been reported [23] . Cavitation model accounts for the turbulence induced pressure fluctuations by simply raising the phase-change threshold pressure from 

where,
After accounting for the effects of turbulence-induced pressure fluctuations and non-condensable gases, the final phase rate expressions are written as Equations (6) and (7):

When,

When, 




A computational grid for the real geometry of diesel injector nozzle is generated and the reliability of the obtained mesh is assessed. The mesh adjacent to the wall should be fine enough to resolve the boundary layer flow as well as meeting the necessary turbulence modeling requirements. The quality of generated mesh has been investigated. As can be seen from Figure 1 when the mesh file is just ensued there is approximately more than 70% of generated cells have skewness between 0.3 and 0.6. That higher skewness leads to lower mesh quality and unreliable CFD simulation results. The right curve of Figure 1 is for the mesh file after the mesh improvement process. From that figure, the quality of the mesh after employing the enhancement process is increased by increasing the number of generated cells. Increasing the cell number from 1000 to 4000 cells means more smooth- ness for the mesh. Also, we can see that the skewness jumped approximately up to 95% and approximately all cells have skewness less than 0.3, and there are no cells have skewness more than 0.5. However, the lower skewness for the mesh leads to higher mesh quality and reliable CFD simulation results.
In this study, stationary diesel, liquid in the nozzle and a sharp liquid interface with the air at the nozzle exit are assumed as initial conditions. Both inflow and outflow boundaries are modeled as constant-pressure surfaces. The boundary conditions for the inlets are taken to be a specified volume flow rate normal to the boundary and enforce the total pressure. The velocities are constrained to be perpendicular to the inlet boundary at each side. On the wall, the boundary conditions are the impermeability and no-slip for the velocity, and the normal gradient of pressure is assumed to be zero. The turbulent effect on the nozzle flow has been employed by the utility of RNG k-ε turbulent model with near-wall treatment with a standard wall function into the nozzle simulation CFD model. The injection rate is assumed to be a steady stream of diesel, liquid with constant flow rate.
As a first step in identifying the relevant physics of injector nozzle flow and cavitation inception, we set out to identify what physical processes were important in studying the internal flow of the nozzle and then conclude the different prevailing factors affect the nozzle cavitating flow. We have investigated the influence of three parameters that can affect the internal flow of the nozzle. The examined parameters consist of the following categories: nozzle geometric parameters which represented by nozzle L/D, nozzle and engine operating parameters represented by the fuel injection pressure as well as the system temperature. Table 1 summarizes the values of accomplished factors from each category.
3. Results and Discussions
3.1. Effect of Nozzle L/D on Flow and Cavitation Inception inside the Injector Nozzle
Under different effective and proper design of diesel injector nozzle, the establishment of the physical laws governing the fluid flow in such nozzle is required in order to understand the behavior of injector nozzle internal flow and fuel cavitation. In fixed operating conditions of injection and cylinder pressure as well as fixed system temperature, we implemented the CFD simulation approach at different length to diameter ratios L/D. The model boundary conditions adjusted with 60 MPa injection pressure, 2 MPa cylinder pressure, and system temperature of 300 K at three values of L/D ratio 2.5, 5, and 7.5.
Figure 2 revealed that when the nozzle L/D is relatively small the liquid is surrounded by a vapor annulus or
Figure 1. Histograms of the generated computational mesh for the real geometry diesel injector nozzle before and after enhancement process.
Table 1. The values of examining parameters used in the CFD simulation.
incomplete reattached flow. By increasing the L/D values the liquid phase moving in the nozzle decay with higher volume fractions to form a higher vapor phase concentration near the nozzle walls and the flow at the nozzle exit is more uniform and accelerated. The increasing rate of forming vapor in the larger L/D values is a result of a higher pressure energy loss which occurs due to the high friction losses near the nozzle walls. If the vapor penetration of the three nozzles is compared, it can be observed that the vapor penetration for the long nozzle is the highest between the three examined nozzles.
It is evident from Figure 3 that with the increase of the injector nozzle L/D ratio the turbulence level increased because the longer passage, resulting in increasing the flow velocities at the nozzle exit section. The velocity magnitude distribution collapses to a single distribution manner, independent of L/D, except a few variations in the velocity profile between the L/D 7.5 and the other two values. The boundary layer thicknesses close to the wall have a small disagreement, at the three L/D values. This discrepancy leads to a difference in the near wall pressure gradient region. The near wall boundary layer pattern is not identical through the different L/D values, thus the larger L/D denote the flow more time to expand and change its flow structure according to the degree of turbulence and density variation along the nozzle length.
3.2. Effect of Injection Pressure on Flow and Cavitation Inception inside the Injector Nozzle
The influence of injection pressure on cavitation and flow field features inside the injector nozzle under diesel engine conditions was simulated. To perform this task the CFD model is adjusted at a constant cylinder pressure of 2 Mpa with the injection pressure values 10 MPa, 30 MPa, 60 MPa, 90 MPa, and 120 MPa at L/D ratio of 5.
Figure 2. Distribution of vapor and liquid concentration inside the nozzle at different L/D and fixed injection pressure 60 MPa, 300 K system temperature.
Figure 3. Distribution of pressure and velocity inside the nozzle at different L/D and fixed injection pressure 60 MPa, 300 K system temperature.
The fuel inlet temperature is assumed to be constant at the atmospheric temperature of 300 K. Figure 4 and Figure 5 elucidates the effect of injection pressure variation on the vapor and liquid concentration, the total pressure distribution (Pa), and velocity magnitude (m/s) inside the injector nozzle at a fixed value of L/D.
The basic features of the cavitating nozzle flow are shown in Figure 4, and Figure 5, which represent the vapor and liquid concentration inside the injector nozzle at different injection pressures. From Figure 5 it is distinct that for a continuous spray condition (steady state), when the injection pressure is 10 MPa, there were some
Figure 4. Distribution of pressure (Pa) and velocity magnitude (m/s) inside the nozzle at different injection pressures and fixed L/D = 5.
emerged vapor distributions at the vena contracta region. The vapor concentration decreased when the flow leaves the wall, but the vapor formed is recondensed with the flow moving down away from the Vienna contracta region and finally the fully developed diesel flow at the nozzle exit was nearly 100% liquid phase. This effect was studied and traced through the results obtained when the injection pressure increased to reach 30 Mpa except that the formed vapor phase continued to exist and increase in its concentration near the walls, but before the nozzle exit suddenly the vapor recondensed and formed a liquid phase with 100% concentration at the nozzle exit section. By increasing the injection pressure more than 30 MPa, exactly at 60 MPa, the continuous liquid phase decayed in its volume fraction near the wall inside the nozzle due to cavitation and the formed vapor presents with a higher percentage until the nozzle exit region. The vapor phase existence at the nozzle exit is more pronounced at higher injection pressures of 90 and 120 MPa. It is clearly shown that cavitation occurs at the entrance region of the injection hole and a larger cavitation region is established on the right-hand side of Figure 5 where the pressure drop from flow deflection and the acceleration are most pronounced. Vapor content is reduced again towards the orifice exit section due to the pressure recovery which may cause condensation.
Figure 5. Distribution of vapor and liquid concentration inside the nozzle at different injection pressures and fixed L/D = 5.
3.3. Thermodynamics/Thermal Effect of Cavitation in Diesel Injector Nozzle
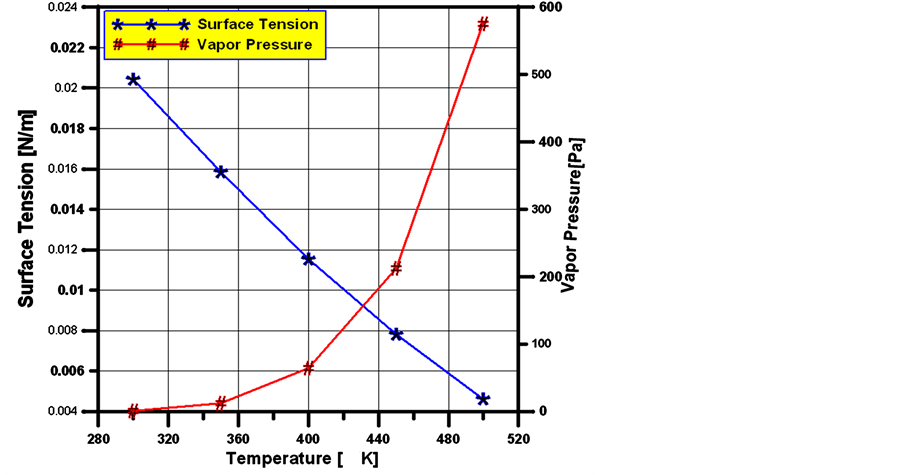
It is widely known that, cavitation in a liquid occurs by lowering the system pressure at an approximately constant temperature. Also, at a constant ambient pressure an increase in the fluid temperature results in a greater aptitude to cavitate. Increasing the temperature of the system will increase the vapor pressure so dramatically because the fraction of the molecules in the fluid sample with sufficient energy to escape as the shackles of their intermolecular forces depends on the energy distribution. Surface tension is caused by the effects of intermolecular forces at the interface. In general, surface tension decreases with temperature as cohesive forces decrease with an increase of molecular thermal activity. So, the effects of temperature on cavitation and flow field characteristics are hereby investigated in this part of our study by applying our simulation CFD model at different values of system temperatures, assuming isothermal flow with no heat transfer, with fixed injection pressure 10 MPa and L/D value 5. As evident from Figure 6, the diesel, liquid surface tension decreases in first order linear manner, while vapor pressure increasing in a second order polynomial manner as the temperature increased.
Figure 7 revealed that the higher temperature of the system at constant pressure, where the vaporization is an endothermic process, the liquid phase vaporization takes place on a large and steady downstream part of the flow. The expecting behavior of cavitating flow inside the injector nozzle with the increase of the degree of thermodynamic effect on the cavity length, particularly increases of its size and existence over the exit section of the nozzle. While, the degree of thermodynamic effect is defined as the reduction of vapor pressure due to the temperature increasing in the system. In addition, the cavitation inside the injector nozzle is more developed and a higher vapor phase concentration appears at the nozzle exit uniformly. Further analytical study of the thermodynamic effect of cavitation is prevailed in Figure 8. It is obviously concluded that the higher degree of thermodynamics in the system leads to a higher flow velocity at the nozzle exit. The zone of strongest depression where cavitation is going to start is located in the separation zone at the upper side of the nozzle. In which, for the small degree of thermodynamics, where the system temperature 300 K, the cavitation zone at the centerline of the nozzle reaches to the highest flow velocity 150 m/s. When cavitation zones decayed, at further length from the nozzle entrance, the flow velocity reduced again at nozzle exit to reach 140 m/s. While, near the nozzle inner boundaries there were larger amount of velocity gradient as a result of friction loss, refers to the portion of pressure lost by fluid while moving through the nozzle. Increase in the system temperature results in a fully developed high velocity fuel flow when exit from the nozzle. Furthermore, there is no pronounced increase in the exit flow velocity as well as the cavitation susceptibility when the system temperature increasing more than 450 K.
4. Conclusions
In this study, the inception of fuel cavitation inside the diesel injector nozzle for a steady state continuous spray condition has been evaluated. The commercial CFD simulation tools (FLUENT-T grid) with the basic governing equations of mass balance, momentum balance, and energy conservation have been utilized. A turbulent, multi phase cavitation CFD simulation approach assigned to investigate the cavitation phenomenon at different operating and geometrical conditions of the diesel injector nozzle. The structured mesh, which can be recognized with all interior nodes of the mesh having an equal number of adjacent elements, is not suitable for relatively complex geometries. While the unstructured mesh, which relaxes the node valence requirement and allowing
Figure 6. Diesel surface tension and vapor pressure as a function of temperature [27] .
Figure 7. Distribution of vapor and liquid concentration inside the nozzle at different system temperatures, nozzle L/D = 5 and injection pressure 10 MPa.
any number of elements to meet at a single node, provides higher quality, adaptively, and parallelizability for complex geometries such as the diesel injector nozzle. The lower skewness for the mesh leads to higher mesh quality and reliable CFD simulation results. Furthermore, after we converted the generated structured mesh to an unstructured mesh the skewness of the mesh cells reduced approximately 80%. The calculations confirm that by increasing the injection pressure the cavitation occurs at the entrance region of the injector’s hole. Also, a larger cavitation region is established on the nozzle upper side where the pressure drop from flow deflection and the acceleration are most pronounced.
When the nozzle L/D is relatively small the liquid is surrounded by a vapor annulus or incomplete reattached flow. While, by increasing the L/D values the liquid phase moving in the nozzle decay with higher volume fractions to form a higher vapor phase concentration near the nozzle walls and the flow at the nozzle exit is more uniform and accelerated. With the increase of the injector nozzle L/D ratio the velocity magnitude distribution
Figure 8. Pressure (Pa) and velocity magnitude (m/second) distributions inside the nozzle at different system temperatures, nozzle L/D = 5 and injection pressure 10 MPa.
collapses to a single distribution manner, independent of L/D, except a few variations in the velocity profile between the L/D equal 7.5 and the other tested values. It is obviously concluded that the higher degree of thermodynamics in the system leads to a higher flow velocity at the nozzle exit. Also, increasing the system temperature results in a fully developed high velocity of the fuel flow when exit from the nozzle. However, there is no pronounced increase in the exit flow velocity as well as the cavitation susceptibility when the system temperature increasing more than 450 K. In addition, vapor formations within the nozzle exhibits oscillatory behavior depending on the nozzle geometry, fuel injection pressure, and system temperature.
References
- Elkelawy, M., Yu-Sheng, Z., El-Din, H.A., Jing-Zhou, Y., El Zahaby, A., El Shenawy, E., et al. (2009) Experimental Study on Flash Boiling and Micro-Explosion of Emulsified Diesel Fuel Spray Droplets by Shadowgraph Technology. Transactions of CSICE, 306-313.
- Ghaffarpour, M., Azarfam, M. and Noorpoor, A. (2006) Emission Reduction in Diesel Engines Using New Fuel Injection System. JSME International Journal Series B, 49, 1298-1306. http://dx.doi.org/10.1299/jsmeb.49.1298
- Senda, J., Wada, Y., Kawano, D. and Fujimoto, H. (2008) Improvement of Combustion and Emissions in Diesel Engines by Means of Enhanced Mixture Formation Based on Flash Boiling of Mixed Fuel. International Journal of Engine Re- search, 9, 15-27. http://dx.doi.org/10.1243/14680874JER02007
- Wang, D., Zhang, C. and Wang, Y. (2007) A Numerical Study of Multiple Fuel Injection Strategies for NOx Reduction from DI Diesel Engines. International Journal of Green Energy, 4, 453-470. http://dx.doi.org/10.1080/15435070701465912
- Gavaises, M. and Andriotis, A. (2006) Cavitation inside Multi-Hole Injectors for Large Diesel Engines and Its Effect on the Near-nozzle Spray Structure. SAE Technical Paper 2006-01-1114. http://dx.doi.org/10.4271/2006-01-1114
- Som, S., Aggarwal, S.K., El-Hannouny, E.M. and Longman, D.E. (2010) Investigation of Nozzle Flow and Cavitation Characteristics in a Diesel Injector. Journal of Engineering for Gas Turbines and Power, 132, Article ID: 042802. http://dx.doi.org/10.1115/1.3203146
- Xue, Q., Som, S., Battistoni, M., Longman, D.E., Zhao, H., et al. (2013) Three-Dimensional Simulations of the Transient Internal Flow in a Diesel Injector: Effects of Needle Movement. ILASS Americas, 25th Annual Conference on Liquid Atomization and Spray Systems, Pittsburgh, 5-8 May 2013.
- Heimgärtner, C. and Leipertz, A. (2000) Investigation of the Primary Spray Breakup Close to the Nozzle of a Common ―Rail High Pressure Diesel Injection System. Society of Automotive Engineers (SAE). SAE Technical Paper 2000- 01-1799. http://dx.doi.org/10.4271/2000-01-1799
- Payri, R., Margot, X. and Salvador, F. (2002) A Numerical Study of the Influence of Diesel Nozzle Geometry on the Inner Cavitating Flow. SAE Technical Paper 2002-01-0215. http://dx.doi.org/10.4271/2002-01-0215
- Delale, C.F., Okita, K. and Matsumoto, Y. (2005) Steady-State Cavitating Nozzle Flows with Nucleation. ASME (Ameri- can Society of Mechanical Engineers) Journal of Fluids Engineering, 127, 770-777. http://dx.doi.org/10.1115/1.1949643
- Yuan, W.X. and Schnerr, G.H. (2003) Numerical Simulation of Two-Phase Flow in Injection Nozzles: Interaction of Cavitation and External Jet Formation. Journal of Fluids Engineering, 125, 963-969. http://dx.doi.org/10.1115/1.1625687
- Von Berg, E., Edelbauer, W., Alajbegovic, A., Tatschl, R., Volmajer, M., Kegl, B., et al. (2005) Coupled Simulations of Nozzle Flow, Primary Fuel Jet Breakup, and Spray Formation. Journal of Engineering for Gas Turbines and Power, 127, 897-908. http://dx.doi.org/10.1115/1.1914803
- Som, S., Senecal, P.K. and Pomraning, E. (2012) Injection Parameter Effects on Diesel Spray Characteristics. 24th Annual Conference on Liquid Atomization and Spray Systems, San Antonio, 21-23 May 2012.
- Payri, F., Bermudez, V., Payri, R. and Salvador, F. (2004) The Influence of Cavitation on the Internal Flow and the Spray Characteristics in Diesel Injection Nozzles. Fuel, 83, 419-431. http://dx.doi.org/10.1016/j.fuel.2003.09.010
- Hasegawa, T., Matsui, K., Iwasaki, T., Kobayashi, T. and Matsumoto, Y. (1998) Injection Characteristics and Spray Fea- tures of the Variable Orifice Nozzle (VON) for Direct Injection Diesel Engines. http://dx.doi.org/10.4271/980807
- Suh, H.K. and Lee, C.S. (2008) Effect of Cavitation in Nozzle Orifice on the Diesel Fuel Atomization Characteristics. International Journal of Heat and Fluid Flow, 29, 1001-1009. http://dx.doi.org/10.1016/j.ijheatfluidflow.2008.03.014
- Schmidt, D.P., Rutland, C.J. and Corradini, M.L. (1997) A Numerical Study of Cavitating Flow through Various Nozzle Shapes. http://dx.doi.org/10.4271/971597
- Kim, J., Nishida, K. and Hiroyasu, H. (1997) Characteristics of the Internal Flow in a Diesel Injection Nozzle. International Journal of Fluid Mechanics Research, 24, 34-44.
- Badock, C., Wirth, R., Fath, A. and Leipertz, A. (1999) Investigation of Cavitation in Real Size Diesel Injection Nozzles. International Journal of Heat and Fluid Flow, 20, 538-544. http://dx.doi.org/10.1016/S0142-727X(99)00043-0
- Takenaka, N., Kadowaki, T., Kawabata, Y., Lim, I. and Sim, C. (2005) Visualization of Cavitation Phenomena in a Die- sel Engine Fuel Injection Nozzle by Neutron Radiography. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 542, 129-133. http://dx.doi.org/10.1016/j.nima.2005.01.089
- Schmidt, D.P. (1997) Cavitation in Diesel Fuel Injector Nozzles. Ph.D. Thesis, University of Wisconsin Madison, Madison.
- Chaves, H., Knapp, M., Kubitzek, A., Obermeier, F. and Schneider, T. (1995) Experimental Study of Cavitation in the Nozzle Hole of Diesel Injectors Using Transparent Nozzles. SAE Technical Paper, No. 950290. http://dx.doi.org/10.4271/950290
- El-Din, H.A., Zhang, Y.S. and Elkelawy, M. (2012) A Computational Study of Cavitation Model Validity Using a New Quantitative Criterion. Chinese Physics Letters, 29, Article ID: 064703. http://dx.doi.org/10.1088/0256-307X/29/6/064703
- Bastawissi, H. and Elkelawy, M. (2012) Computational Evaluation of Nozzle Flow and Cavitation Characteristics in a Diesel Injector. SAE International Journal of Engines, 5, 1605-1616. http://dx.doi.org/10.4271/2012-01-1652
- Fluent Inc. (2014) FLUENT, V6.2, User’s Manual. http://www.ansys.com
- Singhal, A.K., Athavale, M.M., Li, H. and Jiang, Y. (2002) Mathematical Basis and Validation of the Full Cavitation Mo- del. Journal of Fluids Engineering, 124, 617-624. http://dx.doi.org/10.1115/1.1486223
- Rouse, H. and McNown, J.S. (1948) Cavitation and Pressure Distribution: Head Forms at Zero Angle of Yaw. State University of Iowa, Iowa City. http://ir.uiowa.edu/uisie/32