Engineering
Vol.06 No.12(2014), Article ID:51640,13 pages
10.4236/eng.2014.612077
Analytic Solution of MHD Stagnation Point Flow over a Stretching Permeable Surface with Effects of Viscous Dissipation and Joule Heating
Satyaban Panigrahi, Motahar Reza
Department of Mathematics, National Institute of Science and Technology, Berhampur, India
Email: satyabannist@gmail.com, reza@nist.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 September 2014; revised 26 October 2014; accepted 11 November 2014
ABSTRACT
A mathematical analysis is investigated to obtain an analytic solution of magneto hydrodynamic stagnation-point flow towards permeable stretching surface with viscous dissipation and joule heating. In the presence of uniform suction, a transverse magnetic field normal to the surface is applied when the surface is stretched in its own plane with a velocity proportional to the distance from the stagnation-point. The governing nonlinear momentum and energy equations are solved by homotopy analysis method (HAM) to obtain the complete analytic solution and a good agreement is found. The convergence region shows the validity of the HAM solutions. It is observed that the velocity at a point increases/decreases more with increase in the magnetic parameter when the free stream velocity is greater/less than the stretching velocity in presence of suction. An interesting result of the analysis is that, in the presence of suction parameter, the temperature increases with the increase in magnetic parameter at a certain distance from the stretching surface. Near stagnation point on the surface, heat flows from the surface to the fluid and far from the stagnation-point, heat flows from the fluid to surface due to combining effect of ohmic dissipation and strain energy inside the boundary layer.
Keywords:
MHD, Suction, Stretching Surface, Homotopy Analysis Method

1. Introduction
The laminar flow and heat transfer of an incompressible fluid over a stretching surface have significant applications in several technologies of process industry. A number of manufacturing industries process and include both metal and polymer sheets during the production of sheeting materials. This kind of motion of a fluid close to the rigid or stretching surface can be investigated from a standard boundary layer equation. The quality of the final product depends to a large extent on the rate of heat transfer at the stretching surface. It is, therefore, of interest to know the fluid behavior over a stretching surface which determines the rate of cooling. Hiemenz [1] first analyzed an exact solution of the stagnation point flow of a viscous fluid over a rigid surface. The axisymmetric three-dimensional cases for the rigid surface are investigated by Homann [2] . The steady flow of an incompressible viscous fluid over an elastic sheet was studied by Crane [3] where the flow being caused solely by stretching of sheet in its own plane. The temperature distribution in the flow over a stretching surface subject to uniform heat flux was studied by Dutta et al. [4] . The steady two-dimensional orthogonal stagnation point flow of an incompressible viscous fluid towards a stretching surface which is held at constant temperature, was investigated by Mohapatra and Gupta [5] . Later, Mohapatra and Gupta [6] extended his work to study the momentum and heat transfer characteristic of stagnation-point flow of a viscoelastic fluid over a stretching surface. Hassanien [7] analyzed the similarity solution for the flow and heat transfer of a viscoelastic fluid over a stretching sheet. The temperature distribution for the stagnation point flow of a micro polar fluid past a stretching sheet was investigated by Nazar et al. [8] .
In the region of adverse pressure gradient the flow in a boundary layer separates. Due to separation, it leads to increase in drag on the body immersed in the flow and adversely affects heat transfer from the surface of the body. Flow separation can be prevented by applying suction to remove the directed fluid particle from the boundary layer. On the other hand, the wall shear stress and hence friction drag is reduced by blowing. Wall suction and blowing have many applications such as turbine blade cooling, transition delay and prevention separation. The effect of suction on the Hiemenz problem was studied by Schlichting and Bussmann [9] . An approximate solution to the problem of uniform suction is given by Ariel [10] . The effect of uniform suction on the Homann problem where the flat plate oscillates in its own plane is considered by Weidman and Mahalingam [11] . The effect of uniform suction or injection on the two- or three-dimensional stagnation-point flow of a conducting fluid was given by Attia [12] [13] in the presence of an externally applied uniform magnetic field. The effect of uniform suction or injection on two-dimensional stagnation point flow towards a stretching surface with heat generation was given by Attia and Seddeek [14] .
Electrically conducting fluid like a liquid metal, electrolyte or plasma under the influence of magnetic field induces electric current. This type of fluid has many applications in industries, for example, to drive flow, induce stirring, levitation or control heat transfer and turbulence. An exact similarity solution to the MHD boundary layer equations for the steady two-dimensional flow of an electrically conducting incompressible fluid due to the stretching of a plane elastic surface in the presence of a uniform transverse magnetic field was given by Pavlov [15] . Chakrabarti and Gupta [16] studied the MHD flow of a Newtonian fluid over a stretching sheet. In the presence of uniform transverse magnetic field Andersson [17] investigated the MHD flow of a viscoelastic fluid past a stretching surface. Liao [18] developed Homotopy analysis method (HAM) which is one of the most successful and efficient methods to solve a non-linear differential equation. This method is based on a fundamental concept in topology, i.e., Homotopy (Hilton [19] ) which is widely used in numerical techniques (Grigolyuk and Shalashilin [20] ).
In this present work, HAM is employed to find the new analytic solution of the effect of uniform transverse magnetic field as well as suction or blowing on a steady two-dimensional orthogonal stagnation point flow of an electrically conducting fluid towards a permeable stretching surface. For a very small magnetic Reynolds number the induced magnetic field can be neglected. We assume the wall and free stream temperature to be constant.
2. Flow Analysis
Consider the two dimensional stagnation point flow of a viscous incompressible electrically conducting fluid impinging orthogonally to a permeable stretching surface coinciding with plane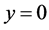 , the being in the region
, the being in the region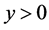 . Two equal and opposite forces are applied to the sheet along the x-axis such that the surface is stretched keeping the origin fixed as shown in Figure 1. The flow is permeated by a uniform magnetic field of strength
. Two equal and opposite forces are applied to the sheet along the x-axis such that the surface is stretched keeping the origin fixed as shown in Figure 1. The flow is permeated by a uniform magnetic field of strength 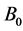 applied transverse to the plate. The plate is assumed to be electrically non-conducting and is subject to uniform suction or blowing.
applied transverse to the plate. The plate is assumed to be electrically non-conducting and is subject to uniform suction or blowing.
Let 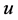 and
and 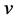 are the velocity components along
are the velocity components along 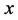 and
and 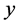 directions, respectively. The velocity in the free flow is given by
directions, respectively. The velocity in the free flow is given by
Figure 1. Physical sketch of the problem.
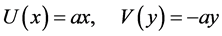 (1)
(1)
where 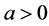 is proportional to the free stream velocity far away from the surface. Under these assumptions, along with the Boussinesq approximation and boundary layer approximations, the governing equations for the steady two-dimensional stagnation point flows by introducing Lorentz force are
is proportional to the free stream velocity far away from the surface. Under these assumptions, along with the Boussinesq approximation and boundary layer approximations, the governing equations for the steady two-dimensional stagnation point flows by introducing Lorentz force are
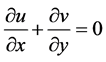 (2)
(2)
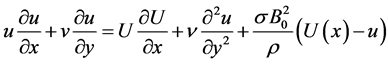 (3)
(3)
 (4)
(4)
where 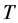 represents the temperature and
represents the temperature and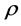 ,
, 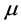 ,
, 









where 





To examine the flow regime, we introduce the following similarity transformation

Here prime denotes differentiation with respect to


where 

In Equation (9) and equating the coefficients of 





where
The corresponding boundary conditions (5) and (6) can be written as



Here 




Using 


Substituting (7) and (16) in (17) we get

where 
3. Homotopy Analysis Solution
The velocity 



as


and

where







and

The auxiliary linear operators




where 






where

Corresponding to the governing differential Equations (8), (11) and (12), we define the non-linear operators as



If








subject to the boundary conditions,


where

When 




Note that when the embedding parameter 
















where



If the auxiliary parameters






Differentiating the zero-th-order Equations (34), (35), (36) 







subject to the boundary conditions



where



and

Let





where







Here the integral constants



Therefore, it is easy to solve linear non-homogeneous Equations (52), (53) and (54) subject to the boundary conditions (55), (56) and (57) by using MATHEMATICA one after other in the order
4. Convergence of Homotopy Solutions
We observed that the Equations (52), (53) and (54) consist of the auxiliary parameters


























5. Results and Discussion
The nonlinear boundary value problem given by Equations (8), (11) and (12) with boundary conditions (13), (14), and (15) cannot be solved in closed form. So these equations are solved by Homotopy Analysis Method (HAM) to get an analytical solution. Extensive calculation has been performed by using symbolic computation software MATHEMATICA to obtain the velocity and temperature profiles for various values of physical parameter such as Suction parameter A, Hartmann Number H, Prandtl number Pr, Eckert number E, (which characterizes viscous dissipation in the flow) and the parameter 







Table 1 shows the value of dimensionless wall shear stress i.e., skin-friction coefficient (see Equation (18)) for several values of H and 



It is observed that during the motion of electrically conduction fluid, a certain amount of energy is stored up in the fluid as strain energy and some energy is lost due to viscous and ohmic dissipation. So in the fluid flow, energy is balanced by the internal energy, the conduction of heat, the convection of heat with the flow, the generation of heat with the flow, the generation of heat through viscous and ohmic dissipation, the strain (or deformation) energy in the fluid and energy due to wall suction effect. At a distance 


In the presence of suction parameter








Figure 2. The 

Figure 3. The h curve of 
Figure 4. Variation of 



Figure 5. Variation of 



Figure 6. Variation of 



Figure 7. Variation of 



Table 1. Values of
suction, viscous and ohmic dissipation and stored deformation energy in the flow












The dimensionless rate of heat transfer at the surface 


where















Since, for small value of




Figure 8. Variation of 





Figure 9. Variation of 





Figure 10. Variation of 




Figure 11. Variation of 




Figure 12. Value of 



6. Conclusion
The present study describes the effect of viscous dissipation and joule heating on magneto hydrodynamic stagnation-point flow towards permeable stretching surface. To analyze the new analytic solution of this problem, we apply homotopy analysis method. By this powerful and newly developed technique, the convergence series solutions are obtained. To validate the analytic solutions of velocity distribution and temperature distribution using HAM method, we have computed the convergence regions. The HAM solutions have an excellent agreement. A novel result of this problem is that the temperature increases with the increase in Hartmann Number H at a certain distance from the stretching surface in the presence of suction parameter. Heat flows from the surface to the fluid at near stagnation point on the surface and on the hand far from the stagnation-point, heat flows from the fluid to surface due to combining effect of ohmic dissipation and strain energy inside the boundary layer.
References
- Hiemenz, K. (1911) Die grenzschicht an einem in den gleichformingen flussigkeitsstrom eingetauchten geraden kreiszylinder. Dingler’s Polytechnic Journal, 326, 321-410.
- Homann, F. (1943) Der einfluss grosser zahighkeit bei der stromung um den zylinder und um die kugel. Zeitschrift für Angewandte Mathematik und Mechanik, 16, 153-164. http://dx.doi.org/10.1002/zamm.19360160304
- Crane, L.J. (1970) Flow Past a Stretching Plate. Zeitschrift für Angewandte Mathematik und Physik, 21, 645-647. http://dx.doi.org/10.1007/BF01587695
- Dutta, B.K., Roy, P. and Gupta, A.S. (1985) Temperature Field in Flow over a Stretching Surface with Uniform Heat Flux. Int. Comm. International Communications in Heat and Mass Transfer, 12, 89-94. http://dx.doi.org/10.1016/0735-1933(85)90010-7
- Mahapatra, T.R. and Gupta, A.S. (2002) Heat Transfer in Stagnation-Point Flow towards a Stretching Sheet. Heat and Mass Transfer, 38, 517-521. http://dx.doi.org/10.1007/s002310100215
- Mahapatra, T.R. and Gupta, A.S. (2004) Stagnation Point Flow of a Viscoelastic Fluid. The International Journal of Non-Linear Mechanics, 39, 811-820. http://dx.doi.org/10.1016/S0020-7462(03)00044-1
- Hassanien, I.A. (2002) Similarity Solutions for Flow and Heat Transfer of a Viscoelastic Fluid over a Stretching Sheet Extruded in a Cross Cooling Stream. Zeitschrift für Angewandte Mathematik und Mechanik, 82, 409-419. http://dx.doi.org/10.1002/1521-4001(200206)82:6<409::AID-ZAMM409>3.0.CO;2-1
- Nazar, R., Amin, N., Filip, D. and Pop, I. (2004) Stagnation Point Flow of a Micropolar Fluid towards a Stretching Sheet. International Journal of Non-Linear Mechanics, 39, 1227-1235. http://dx.doi.org/10.1016/j.ijnonlinmec.2003.08.007
- Schlichting, H. and Bussmann, K. (1943) Exakte Losungen fur die Laminare Grenzchicht mitAbsaugung und Ausblasen. Schriften der Deutschen Akademie der Luftfahrtforschung B, 7, 25-69.
- Ariel, P.D. (1994) Stagnation Point Flow with Suction: An Approximate Solution. Journal of Applied Mechanics, 61, 976-978. http://dx.doi.org/10.1115/1.2901589
- Weidman, P.D. and Mahalingam, S. (1997) Axisymmetric Stagnation Point Flow Impinging on a Transversely Oscillating Plate with Suction. Journal of Engineering Mathematics, 31, 305-318. http://dx.doi.org/10.1023/A:1004211515780
- Attia, H.A. (2003) Hydromagnetic Stagnation Point Flow with Heat Transfer over a Permeable Surface. Arabian Journal for Science and Engineering, 28, 107-112.
- Attia, H.A. (2003) Homann Magnetic Flow and Heat Transfer with Uniform Suction or Injection. Canadian Journal of Physics, 81, 1223-1230. http://dx.doi.org/10.1139/p03-061
- Attia, H.A. and Seddeek, M.A. (2007) On the Effectiveness of Uniform Suction or Injection on Two Dimensional Stagnation-Point Flow towards a Stretching Surface with Heat Generation. Chemical Engineering Communications, 194, 553-564. http://dx.doi.org/10.1080/00986440600992537
- Pavlov, K.B. (1974) Magneto Hydrodynamic Flow of an Incompressible Viscous Fluid Caused by the Deformation of a Plane Surface. Magnitnaya Gidrodinamika, 4, 146-147.
- Chakrabarti, A. and Gupta, A.S. (1979) Hydromagnetic Flow and Heat Transfer over a Stretching Sheet. Quarterly of Applied Mathematics, 37, 73-78.
- Andersson, H.I. (1992) MHD Flow of a Viscoelastic Fluid Past a Stretching Surface. Acta Mechanica, 95, 227-230. http://dx.doi.org/10.1007/BF01170814
- Liao, S.J. (1992) The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai.
- Hilton, P.J. (1953) An Introduction to Homotopy Theory. Cambridge University Press, Cambridge.
- Grigolyuk, E.E. and Shalashilin, V.I. (1991) Problems of Nonlinear Deformation: The Continuation Method Applied to Nonlinear Problems in Solid Mechanics. Kluwer Academic Publishers, Kluwer. http://dx.doi.org/10.1007/978-94-011-3776-8
- Mahapatra, T.R. and Gupta, A.S. (2001) Magnetohydrodynamic Stagnation-Point Flow towards a Stretching Sheet. Acta Mechanica, 152, 191-196. http://dx.doi.org/10.1007/BF01176953
- Mahapatra, T.R., Dholey, S. and Gupta, A.S. (2007) Momentum and Heat Transfer in Magneto Hydrodynamic Stagnation-Point Flow of a Viscoelastic Fluid towards a Stretching Surface. Meccanica, 42, 263-272. http://dx.doi.org/10.1007/s11012-006-9040-8















