Engineering
Vol.06 No.07(2014), Article ID:46715,10 pages
10.4236/eng.2014.67040
A Quick Classification Method of the Power Quality Disturbances
Yi Tang1, Hao Liu1,2
1School of Information and Electrical Engineering, China University of Mining & Technology, Xuzhou, China
2NARI Group Corporation (State Grid Electric Power Research Institute), Nanjing, China
Email: tangyi@cumt.edu.cn, ditfft@126.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 November 2013; revised 5 April 2014; accepted 20 April 2014
ABSTRACT
This paper introduces a quick classification method of the power quality disturbances. Based on analyzing the characteristics of different electrical disturbance signals in time domain, four distinctive features are extracted from electrical signals for classifying different power quality disturbances and then an automatic classifier is proposed. Using the proposed classification method, a PQ monitor of the classifying power quality disturbances is developed based on the TMS320F2812 DSP micro-processor. Semi-physical simulation, lab experiment and field measurement results have verified that this proposed method can classify single or complex disturbance signals effectively.
Keywords:
Power Quality, Disturbance Classification, Noise

1. Introduction
To detect and improve power quality, we first need to monitor and analyze the power quality disturbances. There have been many methods presented, such as Fourier transform [1] , wavelet transform [2] -[4] , S transform and so on. The Fourier transform is suitable to analyze stationary signals, and has a good effect on stationary disturbance like harmonics; the wavelet transform has advantage of analyzing singularity and nonstationary signals [5] [6] ; S transform is the inheritance and development of short-time Fourier transform and wavelet transform. So it has the advantages of the both [7] - [11] . And it analyzes signal features more comprehensively and it has been a hot research tool of power quality disturbance classification. They are all the time frequency transform methods. This paper presents a method based on the time domain analysis of the power quality disturbance signals and it has some advantages compared to the time frequency transform methods. It will be discussed in details in Section 4.
2. The Analysis of Power Quality Disturbances in Time Domain
The general single-phase voltage signal can be expressed as the superposition of the fundamental wave voltage and the disturbance signals:
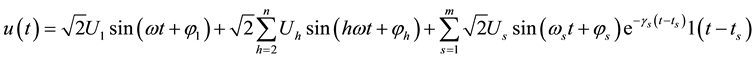 (1)
(1)
where 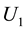 is the RMS (root mean square) voltage with the system fundamental frequency;
is the RMS (root mean square) voltage with the system fundamental frequency;  is the system fundamental angular frequency;
is the system fundamental angular frequency; 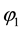 is the initial phase angle;
is the initial phase angle; 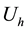 is the hth harmonic RMS voltage;
is the hth harmonic RMS voltage; 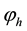 is the hth harmonic initial phase angle;
is the hth harmonic initial phase angle; 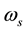 is the angular frequency between harmonic waveforms and not an integer multiple of the system fundamental frequency, for example, the frequencies of interharmonics and oscillatory transients;
is the angular frequency between harmonic waveforms and not an integer multiple of the system fundamental frequency, for example, the frequencies of interharmonics and oscillatory transients; 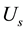 is the
is the 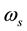 RMS voltage with
RMS voltage with 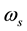 angular frequency;
angular frequency; 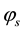 is the initial phase angle of the
is the initial phase angle of the 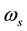 angular frequency voltage;
angular frequency voltage; 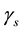 is the oscillatory transient attenuation constant. When
is the oscillatory transient attenuation constant. When ,
, 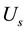 is the interharmonic RMS voltage and when
is the interharmonic RMS voltage and when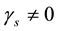 ,
, 

In Equation (1), when 
Equation (1) represents the ideal voltage. So the voltage disturbance can be divided into two categories. One is the disturbances with the change of the 
For voltage sag, swell and interruption has the similar characteristics, the author only takes voltage sag as the analyzing object. The other two can also be identified by the method presented in this paper.
If 


Table 1. Typical characteristics of power system disturbances.
Table 2. The categories of the voltage disturbance.
where, 


Equation (2) consists of three parts. First is DC component












The square of Equation (1) is:

The expanded formula of (3) is long, but also is consists of three parts: DC component



The curve of a full cycle integral of (3) is shown in Figure 2.
By comparing Figure 1 and Figure 2, we can find that Figure 1(a) and Figure 1(b) are the same with Figure 2(a) and Figure 2(b) because there is no additive disturbance in the voltage sag and fluctuation and flicker. The harmonics is additive disturbance, so the Ud/UN in Figure 2(c) is larger than U1/UN in Figure 1(c). And the dif-
ference between them is the amplitude of the additive disturbance
terharmonics are the additive disturbances. So the Ud/UN in Figure 2(d) and Figure 2(e) is larger than the U1/UN in Figure 1(d) and Figure 1(e). And the difference is also the amplitude of additive disturbance



Figure 1. The curve of full cycle integral of (2). (a) Voltage sag; (b) fluctuation and flicker; (c) harmonics; (d) Oscillatory transients; (e) Interharmonics.


Figure 2. The curve of full cycle integral of (3). (a) Voltage sag; (b) Fluctuation and flicker; (c) Harmonics; (d) Oscillatory transients; (e) Interharmonics.
3. Basic Idea of the Classification of the Power Quality Disturbances
Though above analysis, some individual features of the power quality disturbance singles can be shown in time- domain:
1) Equation (2) has the effect of selecting system fundamental frequency. The DC component, which can be gotten by low pass filter from Equation (2), is the RMS voltage with system fundamental frequency, which is not affected by additive disturbance. And its change is equivalent to the amplitude disturbance of the RMS voltage (like voltage sag, swell, transient interrupt, under voltage, over voltage, continuous interrupt, fluctuation, flicker and so on).
2) The DC component of Equation (3) is the geometric sum of the RMS voltage with system fundamental frequency and all other additive disturbance RMS voltages. So the geometric difference of the Equation (3) and Equation (2)’s DC component is exactly equivalent to the amplitude of the additive disturbance (like harmonics, oscillatory transients, impulse voltage and interharmonics).
3) Figure 1(d) and Figure 1(e)’s curves contain 



So, the next 4 features (F1 - F4) can be used to classify power quality single disturbances and the mixed disturbances can be considered as the “superposition” of the single disturbances. The calculating flow chart of the 4 features is shown in Figure 3.
1) 
2)
(for F2 is used to detect stationary additive disturbances, the analysis period of time can be enlarged. This paper takes






3) If


classify the additive disturbances harmonics and interharmonics. If interharmonics exist in Equation (2), the curve of 
Figure 3. The flow chart of calculating classification features.
Table 3. Amplitude change disturbance classifications with F1.
and Figure 1(e)). Then value of 



4)


that the amplitude of instantaneous disturbance changes fast determines 








Table 4 shows the simulation value of 5 single disturbances and 4 mixed disturbances. Figure 4 is the flow chart of the automate classification of the disturbances.
Disturbances can be classified into two categories: voltage amplitude disturbance and additive disturbance as shown in Table 2. 











4. Discussion
Comparing with the other power quality disturbance classification methods using some kinds of transforms, the method presented by this paper has advantages as follows:
1) The single disturbance can be identified by one feature or the combination of some features. That means if one feature or some features satisfied some conditions, a disturbance or mixed disturbances can be sure. Then the disturbance classification will not be probable, but be definitive and the correct rate of the disturbance classification would be very high. And it makes the classification simpler. For example, as shown in Figure 4, if
Figure 4. The flow chart of the automate classification. A: Har- monics + Interharmonics; B: Harmonics; C: Interharmonics; D: No stationary additive disturbance; E:


Table 4. The simulation value of the features.








2) The features extracted from one disturbance won’t change a lot for the existence of the other disturbance. This is shown clearly in Table 4. For example, when the voltage sag and harmonics both exist, 





summation of their amplitude (
ample, 




3) The classifying features have clear physical meanings. So it profits the evaluation of the power quality disturbance. The physical meaning of 






4) The calculating time is much less, and profits to be used in real-time power quality disturbance classification.
5) The features extracted are low-pass filtered or the full cycle integral values, so it has good ability of noise proof.
5. Verifications
Using the proposed power quality disturbance classification method, a PQ monitor is developed based on the TMS320F2812 DSP micro-processor. Semi-physical simulation, lab experiment and field measurement results have verified the proposed method.
5.1. Semi-Physical Simulation Results
The authors use D space semi-physical experiment platform as the disturbance signal generator. The PQ monitor samples the signals generated by D space, identifies disturbances and evaluates their parameters. Table 5 shows that it identifies the disturbance types correctly and evaluates their parameters accurately.
Table 5. The experiments results.
The authors give three types of disturbances: the voltage sag, the voltage sag plus harmonics, the fluctuation plus harmonics plus interharmonics plus voltage sag to present 5 single disturbances and 11 mixed disturbances.
1) The voltage sag
In the following tables the same symbols have the same meanings.
Table 6 doesn’t give the true or false results because the PQ monitor gives the correct results every time. Table 6 shows that the PQ monitor can evaluate the voltage sag parameter very well. The relative error is a little big when the voltage sag amplitude is close to the voltage sag threshold value, but the absolute error is not big.
2) The voltage sag plus harmonics
The authors do not show the identifying results in Table 7, for all harmonics plus voltage sag are identified by the PQ monitor correctly. Table 7 shows that the superposed disturbance doesn’t make the features change a lot, which means the features F2 and F3 are relatively independent. The identifying results and the parameters evaluation are not affected by the superposition of the disturbances.
3) The fluctuation plus harmonics plus interharmonics plus voltage sag
Table 8 shows that the addition of the fluctuation and flicker affects the feature F2 a little, but doesn’t affect the feature F3. The big amount of harmonics may blanket the existence of interharmonics, because the identifying term of the harmonics plus interharmonics is F3/F2 > 0.5.
5.2. Lab Experiment Results
A lab experiment circuit is shown as Figure 5. When the switch S is turned on, there is voltage sag on R1. The voltage signal u1 is sampled by the PQ monitor and the oscilloscope.
U = 380 V, R1 = 1 kΩ, R2 = 2 kΩ, R3 = 3.9 Ω. S is an AC contact. FU is a fuse. When S is turned on and the current of the FU branch is large enough, the FU will blowing out and the branch will be cut off. Then there will be a voltage sag in u1 as shown in Figure 5(b).
The experiment results shown in Table 9 indicate that the PQ monitor can identify disturbances correctly and evaluate the voltage sag lasting time and amplitude accurately.
Table 6. The experiments results of voltage sag.
tm: The voltage sag lasting time measured by the PQ monitor; ts: The setting time of the voltage sag lasting time; et: The error between time 1 and time 2; am: The voltage sag amplitude measured by the PQ monitor; as: The setting amplitude of voltage sag amplitude; ea: The error between amplitude 1 and amplitude 2.
Table 7. The experiments results of harmonics plus voltage sag.
eTHD: The error between the measured THD by PQ monitor and the setting THD.
Table 8. The experiments results of voltage fluctuation plus harmonics plus interharmonics plus voltage sag.
Table 9. The voltage sag experiments results comparison table.
a: Error means the difference between values evaluated by PQ monitor and ones measured by the oscilloscope. For the oscilloscope measured value has error itself, but here, no error is considered. The meaning of error in the other tables is the same.
5.3. Field Measurement Results
A PQ monitor is equipped to a steel pipe factory substation to monitor the harmonics disturbance and the oscillatory transient disturbances. The results are shown in Table 10 and Table 11.
The field monitoring results in Table 10 show that the PQ monitor identifies harmonics correctly and evaluates the THD accurately.
To catch the oscillatory transients, a PQ monitor is equipped to Shi-Qiao substation. The oscillatory transient signals are generated by switching three phase capacitors. The three phase voltage waveform is shown as Figure 6.

Figure 5. The voltage sag experiment. (a) The voltage sag experiment circuit; (b) The waveform of u1.
Figure 6. The three phase voltage waveform of capacitors switching in Shi-Qiao substation.
Table 10. The harmonics experiments results comparison table.
THDm: THD measured by the PQ monitor; THDom: THD measured by the oscilloscope.
Table 11. The experiments results of oscillatory transient in Shi-Qiao substation.
tom: The oscillatory transients lasting time measured by the oscilloscope; aom: The oscillatory transients amplitude measured by the oscilloscope.
The author takes one phase wave to analyze (the purple one). The field experiment results are shown in Table 11.
Table 11 shows that the PQ monitor identifies the oscillatory transients correctly and evaluates their parameters accurately. The difference between the values evaluated by the PQ monitor and ones measured by oscilloscope is small.
6. Conclusion
Comparing with analyzing power quality disturbance signals in frequency domain, the method presented by this paper has some advantages. First, if one feature or some features satisfied some conditions, a disturbance or mixed disturbances can be sure. That is to say, the disturbance classification would not be probable, but be definitive. Second, the features extracted won’t change a lot for the existence of the other disturbances. This characteristic is the key of classifying the mixed disturbances. Third, the features have clear physical meanings. So it profits the evaluation of the disturbance parameters.
References
- Heydt, G.T., Fjeld, P.S., Liu, C.C., et al. (1999) Applications of the Window FFT to Electric Power Quality Assessment. IEEE Transactions on Power Delivery, 14, 1411-1416. http://dx.doi.org/10.1109/61.796235
- Gaing, Z.-L. (2004) Wavelet-Based Neural Network for Power Disturbance Recognition and Classification. IEEE Transactions on Power Delivery, 19, 1560-1568. http://dx.doi.org/10.1109/TPWRD.2004.835281
- Ece, D.G. and Gerek, O.N. (2004) Power Quality Event Detection Using Joint 2-D-Wavelet Subspaces. IEEE Transactions on Instrumentation and Measurements, 53, 1040-1046. http://dx.doi.org/10.1109/TIM.2004.831137
- Chilukuri, M.V. and Dash, P.K. (2004) Multiresolution S-Transform-Based Fuzzy Recognition System for Power Quality Events. IEEE Transactions on Power Delivery, 19, 323-330. http://dx.doi.org/10.1109/TPWRD.2003.820180
- Gaouda, A.M., Salama, M.M.A., Sultan, M.K. and Chikhani, A.Y. (1999) Power Quality Detection and Classification Using Wavelet-Multiresolution Signal Decomposition. IEEE Transactions on Power Delivery, 14, 1469-1476. http://dx.doi.org/10.1109/61.796242
- Santoso, S., Powers, E.J., Grady, W.M. and Hofmann, P. (1996) Power Quality Assessment via Wavelet Transform Analysis. IEEE Transactions on Power Delivery, 11, 924-930. http://dx.doi.org/10.1109/61.489353
- Dash, P.K., Panigrahi, B.K. and Panda, G. (2003) Power Quality Analysis Using S-Transform. IEEE Transactions on Power Delivery, 18, 406-411. http://dx.doi.org/10.1109/TPWRD.2003.809616
- Stockwell, R.G., Mansinha, L. and Lowe, R.P. (1996) Localization of the Complex Spectrum the S Transform. IEEE Transactions on Signal Processing, 44, 998-1001. http://dx.doi.org/10.1109/78.492555
- Axelberg, P.G.V., Gu, I.Y.-H. and Bollen, M.H.J. (2007) Support Vector Machine for Classification of Voltage Disturbances. IEEE Transactions on Power Delivery, 22, 1297-1303. http://dx.doi.org/10.1109/TPWRD.2007.900065
- Mishra, S., Bhende, C.N. and Panigrahi, B.K. (2008) Detection and Classification of Power Quality Disturbances Using S-Transform and Probabilistic Neural Network. IEEE Transactions on Power Delivery, 23, 280-287. http://dx.doi.org/10.1109/TPWRD.2007.911125
- Zhao, F.Z. and Yang, R.G. (2007) Power-Quality Disturbance Recognition Using S-Transform. IEEE Transactions on Power Delivery, 22, 944-950. http://dx.doi.org/10.1109/TPWRD.2006.881575
- IEEE Std 1159-1995 (1995) IEEE Recommended Practice for Monitoring Electric Power Quality.















