Engineering
Vol. 5 No. 9 (2013) , Article ID: 36379 , 6 pages DOI:10.4236/eng.2013.59087
A Study on the Characteristics for the Ground Vibration Due to the Travelling Tilting Train
Structural Engineering Research Division, Korea Institute of Construction Technology, Republic of Korea
Email: lagoon@kict.re.kr
Copyright © 2013 Hee Seok Kim. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 8, 2013; revised August 8, 2013; accepted August 15, 2013
Keywords: Ground Vibration; Tilting Car; Absorbing Boundary
ABSTRACT
The development of the tilting train can contribute to solve the economic burden and enhance the transportation means of areas that did not share the benefits of the high speed railway. But the dynamic behavior caused by the interaction between the train and the track as well as the environmental vibrations along the railway should be evaluated to secure the safety of the train and riding comfort. In this paper a study on the characteristics for ground vibration due to the tilting train travelling in the conventional line are carried out. The transmitted load into the ground is computed through a study on the interrelation between the tilting car and the line. This load is applied into the numerical model which is one for the analysis of ground vibration due to the travelling tilting car. The far fields on the numerical model are formed by the absorbing boundary using dashpot, one of the most widely used absorbing boundary in finite element analysis. Using this numerical model, the analysis of the ground vibration characteristics caused by travelling tilting car is performed. From the analysis, it is shown that the transferred load due to the tilting train is larger than that of the conventional train.
1. Introduction
The Gyeongbu High Speed Railway in Korea increased significantly the speed of the national railway network in a will to reduce the transportation cost of goods and boost the national competitiveness. However, its construction required tremendous cost and time. Besides, the development of the semi high speed/high speed tilting train together with the reshuffling of the alignment to improve the speed while using the existing line make it possible to exploit the established infrastructure. This new option can thus contribute to solve the economic burden and enhance the transportation means of areas that did not share the benefits of the high speed railway like the Jungang Line, Yeongdong Line and Taebaek Line in Korea. Improving the speed by reshuffling the alignment can be achieved by adopting an appropriate cant to prevent the overturning of the vehicle or the loss of riding comfort caused by the centrifugal force in the curved section or by flattening the curve to make it practically straight but such solutions are not only expensive but their applicability is also very limited due to the topographical conditions at hand. Following, adequate solutions should be conceived for the train rather than for the track. The development of the tilting train may constitute such solution with significantly reduced cost while providing a degree of comfort comparable to the high speed train by tilting inward the track as a pendulum in the curved section so as to offer riding stability and comfort to the passenger.
However, the replacement of the existing train running currently at maximum operating speed of 130 km/h by the tilting train traveling at speed beyond 200 km/h will change the operating environment. This stresses the necessity to implement performance evaluation of the existing track crossed by the tilting train including the examination of the wheel force and lateral force on the track, the safety and the riding stability in curved section. In addition, the dynamic behavior caused by the interaction between the train and the track as well as the environmental vibrations along the railway should also be evaluated to secure the safety of the train and riding comfort.
There is thus a serious need in investigating thoroughly the vibration mechanism induced by the interaction between the rail and wheel of the tilting train that will run at high speed on the existing track structure and the characteristics of the ground vibration transmitted to the neighboring structures through the ground during the crossing of the train. Accordingly, this study intends to examine the characteristics of ground vibration caused by the travelling of the tilting train.
The load transmitted to the ground during the traveling of the train is computed by means of the dynamic model analysis of the track and train considering the traveling characteristics of the tilting train. The results of the analysis are then used to identify the loading mechanism and its characteristics. The infinite ground is modeled by numerical element domains by adopting absorbing boundaries using viscous dampers. The computed transferred load is applied to the numerical model to perform numerical analysis. And the corresponding results are exploited to identify the propagation characteristics of the ground vibration due to the tilting train.
2. Computation of the Transferred Load Considering the Dimensional and Traveling Characteristics of the Tilting Train
When the train crosses a straight section, the leftand right-side wheel loads have identical size and are transferred to the ground through the rails. However, in a curved section, the leftand right-side wheel loads have different sizes because of the centrifugal force and the tilting of the train due to the adjusting cant and are transferred to the ground through the rails. Especially, in the case of the tilting train crossing the curved section at higher speed than existing conventional trains, the occurring wheel loads present a pattern different to that of conventional trains due to the difference in the dimensions of the train accompanied with the increase of the centrifugal force and the additional tilting brought by the tilt angle. Accordingly, since the characteristics of the vibration propagating to the ground may also differ, the traveling characteristics of the tilting train must imperatively be reflected in the ground vibration analysis.
This study computes the size of the wheel loads considering the dimensions of the tilting train, the centrifugal force and the tilt angle so as to calculate the load transferred to the ground during the crossing of a curved section.
2.1. Modeling of the Train and Track
The train can be modeled as a two-mass model considering the mass of the train suspension and the mass of the train body as shown in Figure 1.
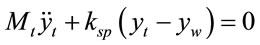 (1a)
(1a)
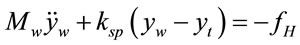 (1b)
(1b)
where yt and yw are the displacements of the train body
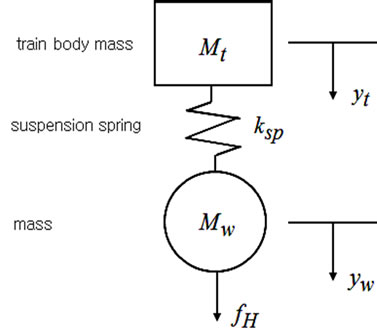
Figure 1. Two-mass model.
and wheels; Mt and Mw are the masses of the body and wheels; ksp is the spring constant of the suspension; and, fH is the interaction force between the train and the track.
The admittance as the transfer function of the system expressing the relation between the load input and the displacement output in the frequency domain computed from Equation (1) is formulated in Equation (2).
 (2)
(2)
where μ = Mt/Mw; and, β2 = ksp/Mt.
In order to compute the train load applied on the ground, the numerical analysis model of the track can be divided into continuously supported model and discretely supported model. Here, the track is modeled using the continuously supported model known to be appropriate for the vibration analysis in the vertical direction at frequency below 200 Hz corresponding to the ground vibration [1]. Moreover, the track is modeled using the continuous double-beam model of Figure 2, which can simulate the ballast track representing more than 90% of the tracks in Korea. The governing equations of the contenuous double-beam model are expressed in Equation (3).
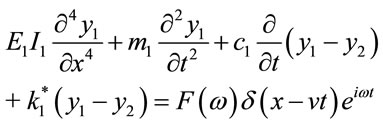 (3a)
(3a)
 (3b)
(3b)
where the subscripts 1 and 2 in Equation (3) indicate the physical properties of the rails and sleepers, respectively; y is the deflection; m and EI are the mass and flexural rigidity per unit length; and, k and c are the complex stiffness and viscous damping per unit length.
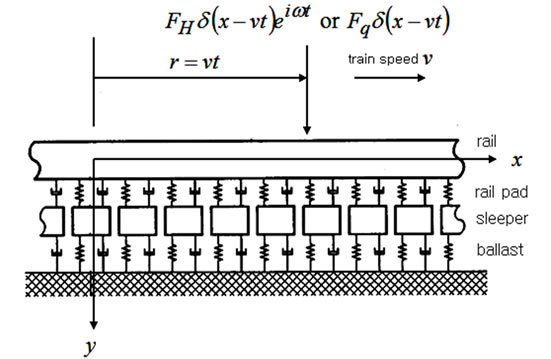
Figure 2. Modeling of track using double-beam model.
2.2. Computation of the Transferred Load Due to the Travelling Tilting Train
Figure 3 displays the basic convoy of the high speed tilting train composed of 6 coaches. The performances and dimensions of the train are arranged in Table 1. Table 2 lists the elevation of the center of gravity of the tilting train in Figure 3.
As shown in Table 2, the elevation of the center of gravity is generally different per type of car. Since the train convoy combines these different cars, applying a different elevation of the center of gravity for each train is difficult. Assuming that the conditions of the track are generally identical, a train with low center of gravity has a higher safety factor for the overturning outward the rails than a train with high center of gravity [2,3]. Figure 4 illustrates the equilibrium of the forces of the tilting train during the crossing of a curved section. Equations (4) and (5) are derived from Figure 4.
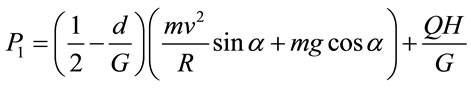 (4)
(4)
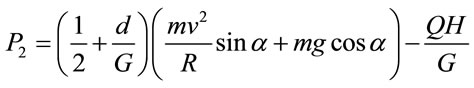 (5)
(5)
where P1 and P2 are the vertical wheel loads applied on the rails; and, G is the horizontal wheel load.
Table 3 compares the speeds of the conventional train and tilting train for the former cant condition when the maximum cant of 150 mm is set as the adjusting cant.
In a curved section, asymmetric wheel loads occur due to the adjusting cant and centrifugal force. Especially, the tilting train exhibits wheel loading with a pattern different to the conventional train because of the dimensions of the train and the differences in the tilt angle and centrifugal force.
Figure 5 plots the vertical and horizontal wheel loads on the left and right sides calculated by Equations (4) and (5) for a train load of 1 ton with respect to the radii of curvature and maximum speeds of Table 3. In Figure 5, the difference in the left and right-side wheel loads of the

Table 1. Performances and dimensions of tilting train.
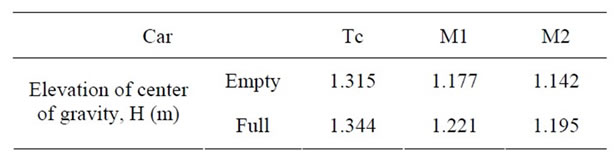
Table 2. Elevation of center of gravity per car.

Figure 3. Basic convoy composition of tilting train.
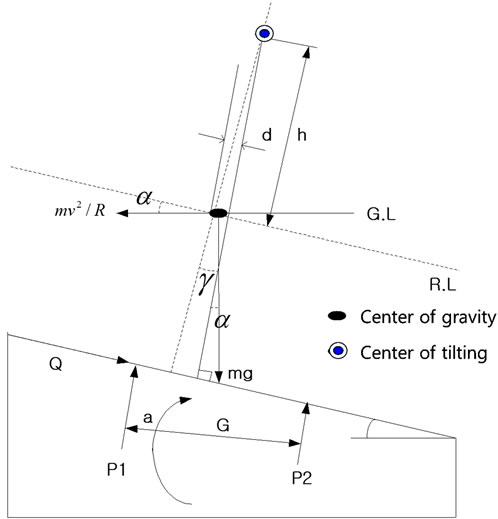
Figure 4. Equilibrium at the center of gravity of the tilting train in a curved section.

Table 3. Maximum speeds according to adjusting cant.
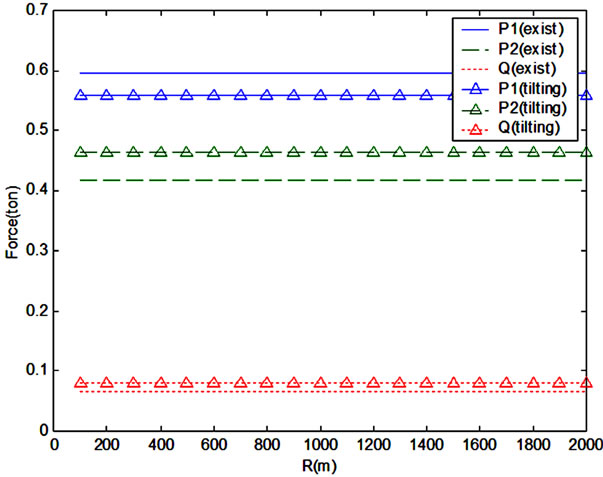
Figure 5. Wheel loads in curved section.
conventional and tilting trains running in a curved section can be clearly observed and can be attributed to the effect of the tilt angle with respect to the increase of the train speed. The difference in the left and right-side wheel loads reduces with the increase of the tilt angle. Moreover, the horizontal force of the tilting train appears also to be slightly larger than that of the conventional train but remains within the value of 0.08 g defined as lateral acceleration by regulations of the National Railways. Since this difference in the wheel loads can result in different propagation characteristics of the ground vibration, this study computes the wheel loads during the crossing of a curved section by reflecting the results of Figure 5 so as to calculate the load transferred to the ground.
In this study, the train load is subdivided into the moving wheel load and the roughness load to obtain the response of the track system caused by each of these components. The response of the track system crossed by the train load is expressed as the sum of these individual responses, and the train load is transferred to the substructure through the response of the track. In other words, the load acting on the rail is transferred to the sleeper via the rail and, the load acting on the sleeper is transferred to the ground via the gravel ballast. When the stiffness of the substructure is significantly larger than the track support stiffness, the load per unit length transferred to the substructure through the track is calculated by Equation (6) using the properties of the rail pad and the deflection of the rail.
 (6)
(6)
where 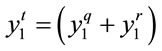 is the sum of the rail deflections due to the moving wheel load and roughness load;
is the sum of the rail deflections due to the moving wheel load and roughness load;  is the train load transferred to the sleepers. More exact results can be obtained by performing three-dimensional analysis in which the train load is modeled by a moving point source. However, two-dimensional analysis is generally conducted in practice due to the difficulties encountered in the scope of the section to be modeled and analysis time [4]. Therefore, the following 2-dimensional equivalent plane load is calculated for the 2-dimensional analysis.
is the train load transferred to the sleepers. More exact results can be obtained by performing three-dimensional analysis in which the train load is modeled by a moving point source. However, two-dimensional analysis is generally conducted in practice due to the difficulties encountered in the scope of the section to be modeled and analysis time [4]. Therefore, the following 2-dimensional equivalent plane load is calculated for the 2-dimensional analysis.
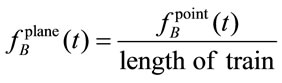 (7)
(7)
where  is the linearly combined concentrated load considering the time delay in time domain due to the moving wheel load and roughness load.
is the linearly combined concentrated load considering the time delay in time domain due to the moving wheel load and roughness load.
Figure 6 compares the PSD of the force transferred to the sleeper by the conventional train and tilting train according to the running speed in a straight section. Here, the peaks occur at various frequencies due to the crossing period of the diverse wheels. It can be also observed that the high frequency contents increase with higher speed. The maximum loads for all the running speeds occur at frequencies below 20 Hz. In addition, the transferred load caused by the tilting train appears to be larger than that of the conventional train. This can be simply explained by the difference in the dimensions of the trains, which result in the occurrence of a larger transferred load induced by the tilting train for the same speed in a straight section. Moreover, if the traveling characteristics in curved section shown in Figure 5 are reflected, the difference in the transferred load will become larger because of the difference in the sizes of the left and rightside wheel loads between the conventional and tilting trains.
3. Propagation Characteristics of Ground Vibration Due to Traveling Train
3.1. Propagation of Vibration in Ground
When the vibration source is disposed on the surface of a uniform half-infinite ground, the vibration energy transferred to the surface propagates by about 67% in the form of surface wave, 26% through shear wave and 7% through body wave [5]. In addition, even if the vibration source is disposed below the surface, the vibration energy rising vertically toward the surface of the layered ground in the form of body wave meets the surface and propagates after having transformed into surface wave.
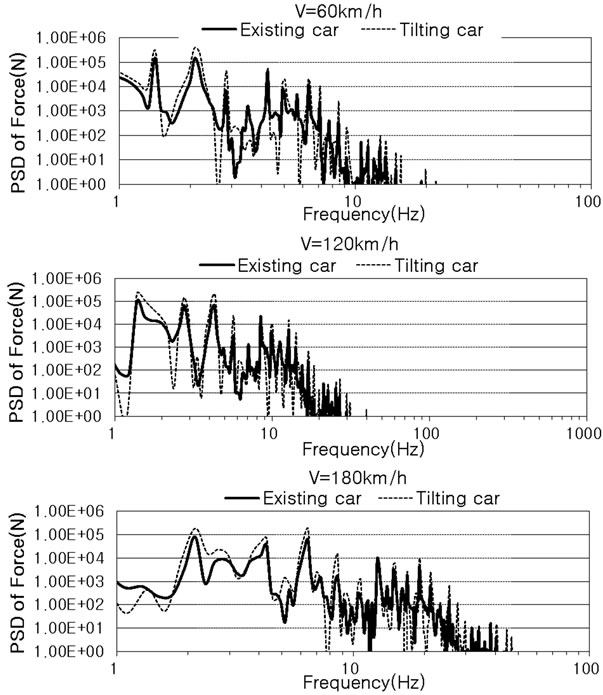
Figure 6. PSD of transferred load according to traveling speed of train (sleeper).
Since this surface wave energy has a lower damping ratio than the body wave propagating directly toward the structure near the surface through the medium, most of the vibration wave at the surface can be assumed to be composed of surface wave. In other words, the ground vibration energy occurring at a point near the surface and located beyond a certain distance from the vibration source can be presumed to be due to the surface wave. Following, the mitigation of the ground vibration should imperatively be done by mitigating the transfer of the surface wave energy.
3.2. Analysis of Ground Vibration Propagation
3.2.1. Numerical Model
In order to minimize the factors influencing the propagation of the vibration, the considered ground is modeled as a single layered ground with identical properties as listed in Table 4.
Since dynamic analysis of the ground like the analysis of vibration propagation must consider the resolution related to the frequency of the occurring stress wave, the computing-time becomes tremendously excessive in most cases. Accordingly, it is recommended to reduce the size of the elements and the analysis time step within the range securing the required resolution [6]. All the frequencies in the numerical model adopted in this study are distributed in a band below 20 Hz. Therefore, the analysis is performed using element size of 2 m and analysis time interval of 0.025 sec enabling to achieve a
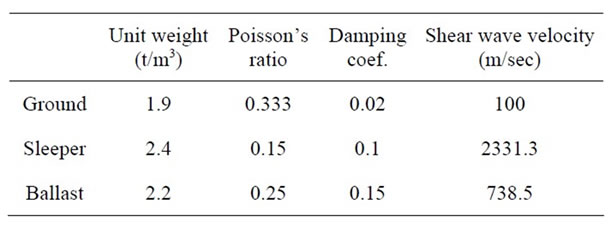
Table 4. Properties of track and ground.
resolution up to 20 Hz for the surface wave. Furthermore, the computing efforts required for the dynamic analysis is reduced by applying absorbing boundaries.
3.2.2. Analysis of Propagation during the Crossing of a Curved Section
When the train travels in a curved section, asymmetric wheel loads occur due to the adjusting cant and the centrifugal force. Especially, the tilting train exhibits wheel loading with a pattern different to the conventional train because of the dimensions of the train and the differences in the tilt angle and centrifugal force. Since the pattern of the vibration propagation can also vary, numerical analysis is performed considering the riding characteristics in a curved section of Figure 5 and the loads of Figure 6. The analysis applies the maximum speeds of the conventional and tilting trains for the radii of curvature computed in Table 3.
Figures 7 and 8 plot the frequency contents of the acceleration per running speed according to the distance from the vibration source. The frequencies are seen to shift toward high frequency band with higher speed because of the characteristics of the load occurrence in Figure 6. Moreover, for identical speeds, the displacements and acceleration at the receiving probe appear to occur identical frequency bands. This last result can be explained by the fact that the shear wave propagates without mode conversion.

Figure 7. Frequency content of acceleration of conventional train.
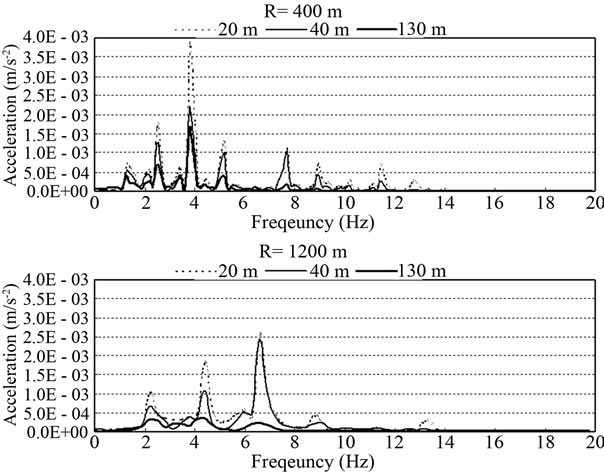
Figure 8. Frequency content of acceleration of tilting train.
4. Conclusions
This study investigated the mechanism by which vibrations occur in an existing track during the crossing of the tilting train using the dynamic models of the track and train. The characteristics of the propagation of the ground vibration produced by the running of the train were evaluated. The following conclusions can be drawn from the results.
1) Computation of the transferred load considering the riding characteristics of the tilting train: the transferred load during the traveling of the tilting train was computed by means of the dynamic analysis of the train and track. The sizes of the wheel loads were calculated considering the dimensions of the tilting train, the centrifugal force and the tilt angle. These wheel loads were then used to compute the load transferred to the ground in a curved section. The characteristics of the left and rightside wheel loads of the conventional and tilting trains appeared to differ due to the increase of the maximum speed and tilt angle caused by the tilting effect during the crossing of the curved section. The transferred load according to the traveling of the conventional train and tilting train exhibited peaks ate different frequencies due to the riding periods of the various wheel loads. Higher frequency contents were observed with the increase of the speed. The peak frequency contents for all the traveling speeds (60 to 180 km/h) occurred in a frequency band below 20 Hz.
When traveling at identical speed, the transferred load due to the tilting train was larger than that of the conventional train.
2) Propagation characteristics of ground vibration occurring during the traveling of train: the deflection and acceleration vibration level were measured to be significantly larger for the tilting train than for the conventional train when running in straight as well as curved sections. Especially, the vibration level appeared to be clearly larger in the direction of the centrifugal force due to the adjusting cant and centrifugal force during the crossing of the curved section. The vibrational frequencies resulting from the displacement and acceleration shifted toward high frequency band with higher train speed. For identical train speed, the peaks of the displacement and acceleration occurred at different frequencies.
In this paper, to minimize the factors influencing the propagation of the vibration, the considered ground was modeled as a single layered ground with identical properties. But the real ground is composed with more complicated layers, hence it is necessary to analyze the model which includes various layers.
REFERENCES
- S. C. Yang, T. O. Kim and Y. S. Kang, “Reduction Methods of Noise and Vibration for Railway Line Structure of High-Speed Train,” Korean Society for Noise and Vibration Engineering, Vol. 14, No. 2, 2004, pp. 26-34.
- Y. H. Yoo, J. H. Um and K. Y. Eum, “Allowable Speed of Tilting Car in the Conventional Line,” Journal of the Korean Society for Railway, Vol. 6, No. 4, 2003, pp. 246-251.
- K. Chung and T. Koh, “Dynamic Interaction Analysis of Tilting Train and Curved Track,” Journal of the Korean Society for Railway, Vol. 15, No. 2, 2012, pp. 162-171. doi:10.7782/JKSR.2012.15.2.162
- K. H. Chua, T. Balendra and K. W. Lo, “Groundborne Vibrations Due to Trains in Tunnels,” Earthquake Engineering and Structural Dynamics, Vol. 21, No. 5, 1992, pp. 445-460. doi:10.1002/eqe.4290210505
- R. D. Woods, “Screening of Surface Waves in Soils,” Journal of the Soil Mechanics and Foundations Division: proceedings of the American Society of Civil Engineers, Vol. 94, No. 4, 1968, pp. 951-979.
- S. S. Jeon, G. Y. Eum and J. M. Kim, “Evaluation of the Roadbed Behavior during Tilting-train Operation in Curved Track Using Numerical Analysis,” Journal of KGS, Vol. 23, No. 6, 2007, pp. 115-126.

