Engineering
Vol.6 No.1(2014), Article ID:42019,8 pages DOI:10.4236/eng.2014.61006
Distributed Generation Effects on Large-Scale Distribution Networks*
Electrical and Computer Engineering Department, Democritus University of Thrace, Xanthi, Greece
Email: #asafig@ee.duth.gr
Received June 12, 2013; revised July 12, 2013; accepted July 19, 2013
ABSTRACT
This paper examines the results of the distributed generation penetration in large-scale medium-voltage power distribution networks. The network examined as a study case consists of twenty one lines fed by three power substations. The injected power comes mainly from photovoltaic units. Specifically, the influences of distributed generation on the network branch currents, losses and voltage profile as well as on the short-circuit level at the medium voltage busbars of the infeeding substations are examined according to international and national standards. The arising problems are explored and technical solutions are proposed. This paper is a pilot application as general conclusions concerning the extended distributed generation penetration in real power distribution networks are set out.
Keywords:Distributed Generation Effects; Extended Penetration; Technical Constraints; Thermal Current; Losses; Short-Circuit Level; Voltage Profile
1. Introduction
In recent years, increasing amounts of distributed generation (DG) have been connected to distribution networks. Environmental, technical, and economic issues are playing an important role in the development of DG.
A general definition for DG was suggested in [1] and is now widely accepted: “Distributed generation is an electric power source connected directly to the distribution network or on the customer site of the meter”. This definition does not determine the rating of the generation sources or the DG technologies used. Furthermore, it does not cover power delivery area, penetration, ownership, or treatment within the network operation.
As a result of DG penetration at distribution level, distribution systems are facing the challenge of evolving from passive networks with unidirectional power flow supplied by the transmission grid to active networks with bidirectional power flows. A number of steps should be followed concerning, on the one hand, best use of the existing distribution network by optimal allocation of the DG resources and, on the other hand, optimal planning of the development from passive to active, by taking account of all the relevant technical and commercial considerations. The technical issues include the adequacy of the network’s and associated plant’s thermal rating, fault levels, and sufficient voltage support to ensure both the security and quality of electricity supply [2-7]. The commercial issues include the cost of the DG, installation charges, operating costs, revenue expectations, and the value of reduced losses in the network [8-12].
The challenge is to identify suitable DG locations and ratings in distribution networks with respect to technical or economic constraints, which will enable a high DG penetration and avoid network sterilisation which results when capacity is allocated to bus/buses whose voltage and/or short-circuit levels (SCLs) are most sensitive to power injections. Thus, no more generation can be connected as the buses are constrained [4,7].
Although the optimal DG allocation on distribution networks is the most interesting research point, the most common practical question is whether DG resources of a particular type and rating can be connected at predetermined network positions without causing technical problems [6] and, if possible, without changing the network structure. This is determined by the specific requirements of independent producers.
In Greece, during the last years, a huge number of independent producer applications were submitted for approval, mainly concerning the connection of photovoltaic (PV) units to the Public Power Corporation (PPC) Medium Voltage (MV) distribution network. The Greek Government subsidises the production of these “green” kWhs in order to meet the environmental constraints established by the Kyoto Protocol and other government initiatives primarily concerning fuel saving. The aforementioned applications are very difficult to be examined in detail. So, there is a possibility that the existing MV networks will not be able to accommodate the new generation, operating in parallel, in a technically and economically acceptable manner.
In light of the above situation, this paper investigates the results of DG penetration in a large-scale MV distribution network as a pilot application. The network is fed by three power substations and it consists of twenty one MV lines. The DG resources to be connected are mainly PV units, with a total capacity of about 32 MW. Their locations are predetermined. Specifically, the influence of these units on the network branch currents, voltage profile, power flow, short-circuit level (SCL) at the MV busbars of the infeeding power substations, and losses are examined using a commercial-grade software package. The results arising from this real-world case study can be used as a pilot for the relevant analysis required for every relative network.
2. Network Description
The network examined in this paper is the rural MV network of the prefecture of Xanthi, Greece. This prefecture has an area of 1793 square kilometers and a population of 100,000 inhabitants.
The total MV network of the prefecture of Xanthi is illustrated in Figure 1. It is fed by the three power substations, 150/20 kV, of Xanthi, Magiko, and Iasmos. The substation of Xanthi has a rated capacity equal to 100 MVA (2 × 50 MVA) and a short-circuit level SCLmax = 138 MVA, the substation of Magiko has a rated capacity equal to 100 MVA (2 × 50 MVA) and a short-circuit level SCLmax = 129 MVA, and the substation of Iasmos has a rated capacity equal to 50 MVA (2 × 25 MVA) and a short-circuit level SCLmax = 230 MVA. The substation of Iasmos feeds, in part, Xanthi prefecture and, in another part (one line), the neighbouring Rodopi prefecture.

Figure 1. Sketch of the power substations and the MV lines of the examined network.
In this paper, only the lines belonging to the prefecture of Xanthi are examined. The substation of Xanthi feeds with four lines the town of Xanthi (urban network). These lines are not examined in this paper because they do not have DG units connected. So, the twenty one lines examined constitute the rural network of Xanthi, and their allocation to the three power substations is outlined in Figure 1 and Table1 The types of conductors used in these lines are:
• ACSR 3 × 95 mm2 and ACSR 3 × 50 mm2 for the main feeders, and
• ACSR 3 × 35 mm2 and ACSR 3 × 16 mm2 for the secondary branches.
The total length per line is given in Table1
The nominal voltage of the MV buses is 20 kV, while their operating voltages are:
• For the maximum load: 21.4 kV
• For the daily minimum (evening) load: 21 kV
• For the absolutely minimum (night) load: 20.5 kV.
Given in Table 1 are the maximum recorded loads of the examined lines, for the examined year, measured by the PPC of Xanthi. The daily minimum (evening) load is
taken as equal to 70% of the maximum load, while the absolutely minimum (night) load is taken as equal to 20% of the maximum load, following relevant PPC suggestions.
Table 1 also shows the overall installed distribution substation capacity per line. This capacity concerns both the PPC distribution substations and the distribution substations of the individuals. Since annual peak load measurements per PPC distribution substation are not available, the rated power of each substation is coincided with the maximum recorded load per line, following relevant suggestions and based on PPC data. Specifically, for each line, the maximum load of the individuals recorded was subtracted from its maximum load, and a coincidence factor for the PPC distribution substations installed in the line was then determined by dividing the remaining line load by the cumulative rated power of these substations. The product of the coincidence factor and the rated power of each substation gives the contribution of the substation to the maximum load of the line. The total coincided load per line is also given in Table1 All the loads are considered to operate with a common inductive power factor equal to 0.9 with the exception of the loads of line M36 which, according to PPC suggestions, is considered to operate with a common inductive power factor equal to 0.89.
The total DG power per line (existing or scheduled to be connected) is also shown in Table1 This power comes mainly from PV units, which operate with a capacitive power factor equal to 0.99, except for the line X22, where two small hydroelectric plants are connected, having a rated power equal to 2.36 MW and operating with a power factor equal to unit. The already existing DG power per line is shown in a separate column of Table1 This power is taken into account in the computations for the existing situation.
Fixed and switched capacitors connected to the lines are also given in Table1
The network was captured and examined using the NEPLAN software package [13].
3. Technical Constraints
The following technical constraints are taken into account throughout the investigation of the DG penetration in the examined network:
1) SCL Constraint: a basic requirement for permitting the interconnection of DG is to ensure that the resulting SCL remains below the network design value (SCLrated). The SCL is highest at the MV busbars of the infeeding substation (SCLmax). The following relation describes the constraint:
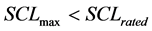 (1)
(1)
2) Transformer Capacity: the amount of generation connected minus the minimum load must not exceed the rating of the transformer at the higher voltage.
3) Thermal Constraint: the rated current of the lines, Iirated, must not be exceeded:
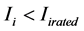 (2)
(2)
where Ii is the current flowing at each network branch.
4) Voltage Variation Constraint: A critical consideration concerning the interconnection of DG sources to the grid is their effect on the slow voltage variations. Therefore the utility operators should impose certain limits within which the voltage variations should lie during normal network operation. The statistical nature of voltage variations is now recognised and relevant norms have been issued, such as the European Norm EN 50160 [14], which impose statistical limits, where a small probability of exceeding them is acceptable. However, checking the conformity against statistical limits at the planning stage requires elaborate procedures, such as probabilistic load flow techniques. Such an approach is relatively difficult to apply because it requires data usually unavailable in practice, which completely defeats the objective of simplicity and efficiency in the evaluation. For this reason, utility directives for the connection of DG adopt simpler and more straightforward procedures while also differentiating their requirements from those imposed by EN 50160 [15].
According to [14], and for the public MV networks, the 10-minute mean rms voltage values are between 90% and 110% of the nominal voltage UN during 95% of a period of one week.
As mentioned above, while EN 50160 gives general limits for public supply networks, various European countries have additional rules governing supply conditions. So, in Greece and for the PPC MV networks, the following requirements are set for the steady-state node voltages, according to [15,16]:
• The median voltage of any node i should lie within ±5% of the nominal voltage UN, a requirement dictated by the off-load tap changer of the MV/LV distribution transformers (±5% regulation, in steps of 2.5%):
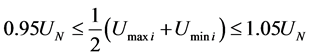 (3)
(3)
where Umaxi and Umini are the maximum and minimum voltage values in the node i, determined by solving the load flow for all combinations of max/min load/generation (usually, minimum load/maximum generation yields maximum voltage values and maximum load/minimum generation yields minimum voltage values).
• The variation of the voltage around its median value should not exceed ±3% of the nominal, so that the LV network voltage deviations remain within ±8% (planning limit), after the median deviation is corrected by the fixed taps:
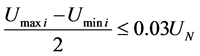 (4)
(4)
4. Network Study
According to the data of Table 1, the total DG rated power in the lines stemmed from Xanthi substation is 13.55 MW, in the lines stemmed from Iasmos substation is 6.4 MW, and in the lines stemmed from Magiko substation is 11.8 MW.
For the SCL computation, the IEC60909 [17] was used. In particular, the computation of the contribution of the PV units to SCL was made using the following equation given in [18]:
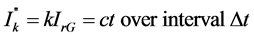 (5)
(5)
where:
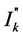 the initial symmetrical short-circuit current k = 1.5 - 2.0 and Δt is the duration of the contribution
the initial symmetrical short-circuit current k = 1.5 - 2.0 and Δt is the duration of the contribution
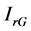 the rated current of the PV unit.
the rated current of the PV unit.
The value of k selected for this paper was equal to 2. The fault current contribution of all the PV units is simply added algebraically to the total fault level of all other sources, which provides a result slightly on the safe side. The PPC takes the negligible fault current contribution of the PV units as zero.
Table 2 shows the fault current contribution of the DG units to SCLmax for each one of the three power substations. From the data of Table 2, it is obvious that the SCL constraint outlined in Section 3 is not breached. Only the substation of Iasmos has an SCLmax very close to its design value (SCLrated = 250 MVA), which must be
Table 3 Line currents and losses for the limit network operating situations.
seriously considered, as there is an additional MV line departing from this substation towards the Rodopi prefecture. Additional DG units may be connected to this line, which will increase the SCLmax of Iasmos substation even further.
The power flow, voltage profile, currents, and losses of the network lines were examined through power flow analysis using the NEPLAN software package. Specifi cally, the following limit network operating situations were examined in order to find the worst scenario:
S1. Maximum load, zero DG penetration (PV and hydroelectric units out of service).
S2. Maximum load, maximum DG penetration (full operation of PV and hydroelectric units).
S3. Daily minimum load, zero DG penetration.
S4. Daily minimum load, maximum DG penetration.
S5. Absolutely minimum (night) load, zero DG penetration.
S6. Absolutely minimum (night) load, maximum night DG penetration (full operation of the hydroelectric units only).
The last situation S6 concerns only the line X22, which has two small hydroelectric units of a total power equal to 2.36 MW. These units continue to contribute to the load during the night, when the absolutely minimum load exists and the PV units do not produce power.
Table 3 shows the results of the power flow analysis concerning the departure current, the maximum recorded ratio Ii /Iirated of the branch current Ii as a percentage of the rated current Iirated of the conductor used in this branch, and the total active Ploss and reactive Qloss losses per line, for the first four of the above mentioned limit operating situations.
The DG penetration reduces the departure current. The greater the DG penetration, the greater this reduction is. In the S4 case, there is an inverse power flow for the lines X33, X36, M36, M37, M39, I21, and I22, as shown by the negative sign of the departure current in the shaded cells of Table3 Even in the case of coincided reverse currents, the total reverse current per power substation corresponds to a reverse power flow much smaller than its capacity. So the second technical constraint (Transformer Capacity) is satisfied. The third technical constraint (Thermal Constraint) is also satisfied, as shown by the values of the ratio Ii /Iirated % in Table 3, which are mostly much smaller than 100%.
The active losses Ploss are reduced when the DG units are connected, for all the network operating situations, as a comparison of the relevant columns of Table 3 shows. An increase of the active losses appearing in the line M37 (shaded cells) for the daily minimum load is mainly due to a 2 km ACSR 3 × 16 mm2 line connecting a 2 MW PV unit, which is planned for construction, and it is not taken into account in the examination of the S3 net
work operating situation. The active losses of the other M37 line branches are reduced.
The reactive losses Qloss are also reduced when the DG units are connected, except for two cases (lines X22 and I21), shown with shaded cells in Table 3, where the daily minimum load in combination with considerable DG penetration causes an increase in the reactive losses.
Table 4 shows the results of the power flow analysis concerning the limit values of the node voltages of the examined network. Specifically, the absolutely maximum node voltages Umax,maxi, the absolutely minimum node voltages Umin,mini, the maximum value of the median voltage, and the maximum value of the quantity Umaxi -Umini per line are recorded.
Taking into account that the nominal voltage of the examined network is 20 kV, the EN 50160 [14] is satisfied if the node voltages remain inside the range 18 kV ≤ Ui ≤ 22 kV. This does not apply only for the line X22, where the possible operation of the hydroelectric units during the night (operating situation S6), in combination with the fixed capacitors, causes voltage rise exceeding the acceptable limits in some nodes.
The requirements of [15,16] are satisfied for the data of the examined network if 19kV ≤ (Umaxi + Umini)/2 ≤ 21 kV and Umaxi − Umini ≤ 1.2 kV. The first requirement is not satisfied for the majority of the lines according to the
upper limit, but the excess, although concerning enough nodes, is marginal. Only the line X22 has a remarkable problem, according to the second requirement, concerning many nodes near the connection point of a 1.08 MW hydroelectric plant and the simultaneous existence of a 900 kVAr fixed capacitor near it. Several alternative scenarios were examined in order to overcome the problem, and the operation of the network was significantly improved by replacing the fixed capacitor with switched capacitors. Otherwise, the above mentioned hydroelectric plant is not permitted to be connected, in order to avoid exceeding the technical constraints.
5. Conclusions
The purpose of this paper was to investigate the impacts of DG penetration in a real rural MV power distribution network. The network is very extensive, consisting of twenty one overhead lines fed by three power substations.
Power flow and short-circuit analysis were carried out using a commercial-grade software package to determine the changes caused by the DG penetration to the currents, losses, voltage profile, and short-circuit level of the examined lines. The majority of the DG units to be connected are PV units, the penetration is not very high, and the connection points are at sublateral branches with small cross sections.
The results of the analysis are as follows:
• The losses are reduced in all the lines when the DG units are connected.
• There is not any extension of the conductor rated currents, since the DG penetration remains small compared to the load and there is also no significant reverse power flow.
• The short-circuit level at the MV busbars of the infeeding substation, where it has the highest value, remains below the network design value, as the DG units are connected at remote sites and the lines have many kilometres of conductors with small cross section (high resistance).
• The main impact of the connected DG units is on the voltage profile of the examined lines, particularly for the daily minimum load (voltage rise) and for lines with fixed capacitors. In these cases, except for the appropriate regulation of the transformer tap changer, solutions should be sought, such as the replacement of the fixed capacitor with switched capacitors.
The general conclusion is that the arbitrary DG accommodation leads to network sterilisation, as recorded in [6,7], and perhaps to violation of important technical constraints. So, every new DG penetration in any network must be examined using the appropriate tools in order to find solutions to the problems that arise.
The extended accommodation of PV resources in a distribution network reduces the losses, because of their close vicinity to the network loads. However, as the PV units operate with a capacitive power factor, they cause impermissible voltage rise during the low load periods. So, either a differentiation in the power factor of the PV units or an integration of voltage control methods is appropriate in order to avoid problems relating to the network voltage profile.
6. List of Symbols
Ii: current of the branch i Iirated: rated current of the branch i
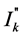 : initial symmetrical short-circuit current
: initial symmetrical short-circuit current
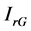 : rated current of the PV unit Ploss: active losses Qloss: reactive losses SCL: short-circuit level SCLmax: maximum short-circuit level
: rated current of the PV unit Ploss: active losses Qloss: reactive losses SCL: short-circuit level SCLmax: maximum short-circuit level
SCLrated: short-circuit level network design value Ui: voltage value in the node i UN: nominal voltage value
Umaxi: maximum voltage value in the node i Umax,maxi: absolutely maximum node voltage value in the node i Umini: minimum voltage value in the node i Umin,mini: absolutely minimum node voltage value in the node i
REFERENCES
- T. Ackermann, G. Andersson and L. Soder, “Distributed Generation: A Definition,” Electric Power Systems Research, Vol. 57, No. 3, 2001, pp. 195-204. http://dx.doi.org/10.1016/S0378-7796(01)00101-8
- A. Wallace and G. Harrison, “Planning for Optimal Accommodation of Dispersed Generation in Distribution Networks,” Proceedings of the CIRED 17th International Conference on Electricity Distribution, Barcelona, May 2003, 6 p.
- A. Bhowmik, A. Maitra, S. M. Halpin and J. E. Schatz, “Determination of Allowable Penetration Levels of Distributed Generation Resources Based on Harmonic Limit Considerations,” IEEE Transactions on Power Delivery, Vol. 18, No. 2, 2003, pp. 619-624. http://dx.doi.org/10.1109/TPWRD.2003.810494
- A. Keane and M. O’Malley, “Optimal Allocation of Embedded Generation on Distribution Networks,” IEEE Transactions on Power Systems, Vol. 20, No. 3, 2005, pp. 1640-1646. http://dx.doi.org/10.1109/TPWRS.2005.852115
- G. Celli, E. Ghiani, S. Mocci and F. Pilo, “A Multi-Objective Evolutionary Algorithm for the Sizing and Siting of Distributed Generation,” IEEE Transactions on Power Systems, Vol. 20, No. 2, 2005, pp. 750-757. http://dx.doi.org/10.1109/TPWRS.2005.846219
- G. N. Koutroumpezis, A. S. Safigianni, G. S. Demetzos and J. G. Kendristakis, “Investigation of the Distributed Generation Penetration in a Medium Voltage Power Distribution Network,” International Journal of Energy Research, Vol. 34, No. 7, 2010, pp. 585-593.
- G. N. Koutroumpezis and A. S. Safigianni, “Optimum Allocation of the Maximum Possible Distributed Generation Penetration in a Distribution Network,” Electric Power Systems Research, Vol. 80, No. 12, 2010, pp. 1421-1427. http://dx.doi.org/10.1016/j.epsr.2010.06.005
- B. Kuri, M. Redfern and F. Li, “Optimization of rating and positioning of dispersed generation with minimum network disruption,” Proceedings of the IEEE Power Engineering Society General Meeting, Denver, June 2004, pp. 2074-2078.
- K. Nara, Y. Hayashi, K. Ikeda and T. Ashizawa, “Application of Tabu Search to Optimal Placement of Distributed Generators,” Proceedings of the IEEE Power Engineering Society Winter Meeting, 2001, pp. 918-923.
- G. Celli and F. Pilo, “Optimal Distributed Generation Allocation in MV Distribution Networks,” Proceedings of the 22nd IEEE PES International Conference on Power Industry Computer Applications PICA, Sydney, 20-24 May 2001, pp. 81-86.
- K. H. Kim, Y. J. Lee, S. B. Rhee, S. K. Lee and S. K. You, “Dispersed Generator Placement Using Fuzzy-GA in Distribution Systems,” Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, 21-25 July 2002, pp. 1148-1153. http://dx.doi.org/10.1109/PESS.2002.1043458
- W. El-Khaltam, K. Bhattacharya, Y. Hegazy and M. M. A. Salama, “Optimal Investment Planning for Distributed Generation in a Competitive Electricity Market,” IEEE Transactions on Power Systems, Vol. 19, No. 3, 2004, pp. 1674-1684. http://dx.doi.org/10.1109/TPWRS.2004.831699
- http://www.neplan.ch/html/e/e_home.htm
- European Norm EN 50160: Voltage Characteristics of Electricity Supplied by Public Distribution Systems, CENELEC, 1999.
- S. A. Papathanassiou, “A Technical Evaluation Framework for the Connection of DG to the Distribution Network,” Electric Power Systems Research, Vol. 77, No. 1, 2007, pp. 24-34. http://dx.doi.org/10.1016/j.epsr.2006.01.009
- Technical Requirements for the Connection of Independent Generation to the Grid, Public Power Corporation (PPC), Greece, 2004.
- IEC 60909-0: Short-Circuit Currents in Three-Phase a.c. Systems, Parts 0-4, 2002.
- T. Boutsika and S. A. Papathanassiou, “Short Circuit Calculations in Networks with Distributed Generation,” Electric Power Systems Research, Vol. 78, No. 7, 2008, pp. 1181-1191. http://dx.doi.org/10.1016/j.epsr.2007.10.003
NOTES
*This paper contains the final processed results concerning the examined subject. Relevant early results were presented in the 11th Euro PES 2012, June 25-27, Napoli, Italy.
#Corresponding author.


