Engineering
Vol.5 No.5A(2013), Article ID:31823,6 pages DOI:10.4236/eng.2013.55A006
On Some I-Convergent Double Sequence Spaces Defined by a Modulus Function
Department of Mathematics, Aligarh Muslim University, Aligarh, India
Email: vakhanmaths@gmail.com, nazneen4maths@gmail.com
Copyright © 2013 Vakeel. A. Khan, Nazneen Khan. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 15, 2013; revised March 17, 2013; accepted March 26, 2013
Keywords: Ideal; Filter; Modulus Function; Lipschitz Function; I-Convergence Field; I-Convergent; Monotone and Solid Double Sequence Spaces
ABSTRACT
In 2000, Kostyrko, Salat, and Wilczynski introduced and studied the concept of I-convergence of sequences in metric spaces where I is an ideal. The concept of I-convergence has a wide application in the field of Number Theory, trigonometric series, summability theory, probability theory, optimization and approximation theory. In this article we introduce the double sequence spaces 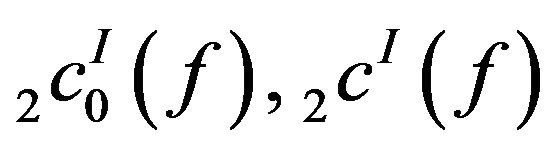 and
and  for a modulus function f and study some of the properties of these spaces.
for a modulus function f and study some of the properties of these spaces.
1. Introduction
The notion of I-Convergence is a generalization of the concept statistical convergence which was first introduced by H. Fast [1] and later on studied by J. A. Fridy [2,3] from the sequence space point of view and linked it with the summability theory. At the initial stage I-Convergence was studied by Kostyrko, Salat and Wilezynski [4]. Further it was studied by Salat, Tripathy, Ziman [5] and Demirci [6]. Throughout a double sequence is denoted by 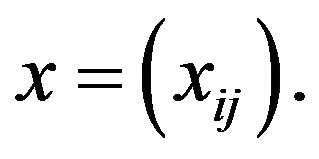 Also a double sequence is a double infinite array of elements
Also a double sequence is a double infinite array of elements 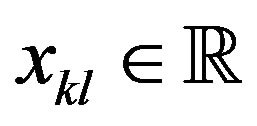 for all
for all 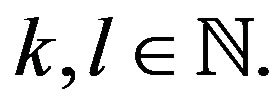 The inital works on double sequences is found in Bromwich [7], Basarir and Solancan [8] and many others.
The inital works on double sequences is found in Bromwich [7], Basarir and Solancan [8] and many others.
2. Definitions and Preliminaries
Throughout the article 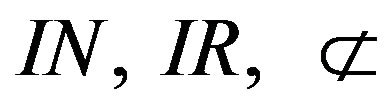 and
and ![]() denotes the set of natural, real, complex numbers and the class of all sequences respectively.
denotes the set of natural, real, complex numbers and the class of all sequences respectively.
Let X be a non empty set. A set  (
(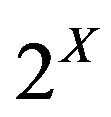 denoting the power set of X) is said to be an ideal if I is additive i.e
denoting the power set of X) is said to be an ideal if I is additive i.e 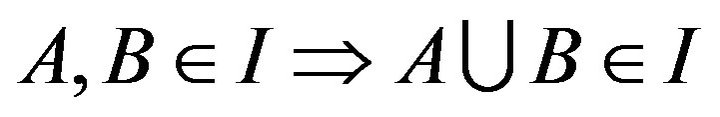 and hereditary i.e.
and hereditary i.e.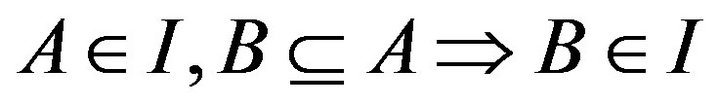 .
.
A non-empty family of sets 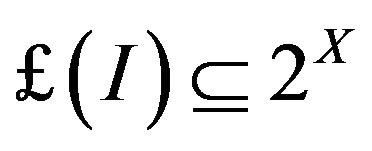 is said to be filter on X if and only if
is said to be filter on X if and only if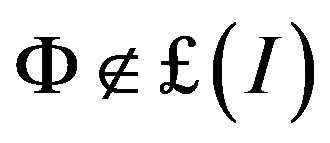 , for
, for 
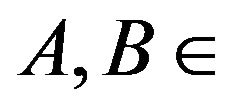 we have
we have 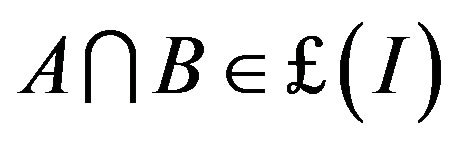 and for each
and for each 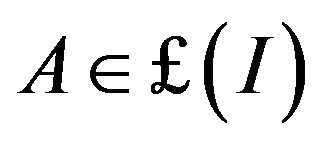 and
and 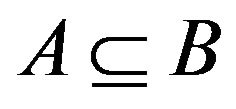 implies
implies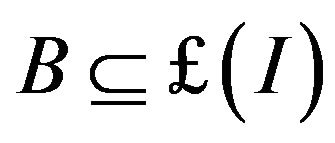 .
.
An Ideal 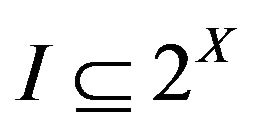 is called non-trivial if
is called non-trivial if .
.
A non-trivial ideal 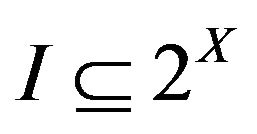 is called admissible if
is called admissible if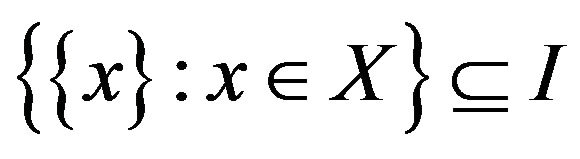 .
.
A non-trivial ideal I is maximal if there cannot exist any non-trivial ideal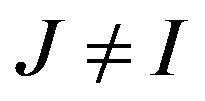 containing I as a subset.
containing I as a subset.
For each ideal I, there is a filter 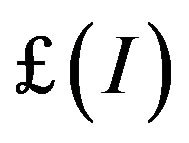 corresponding to I.
corresponding to I.
i.e.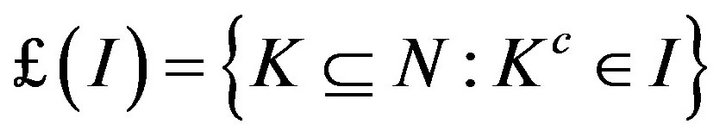 , where
, where .
.
The idea of modulus was structured in 1953 by Nakano (See [9]).
A function 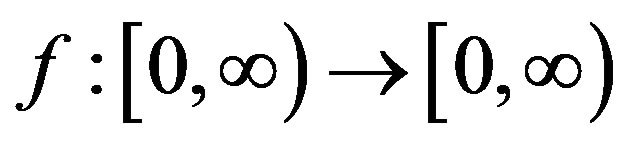 is called a modulus if
is called a modulus if
(1)  if and only if
if and only if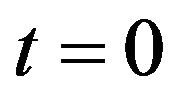 (2)
(2) 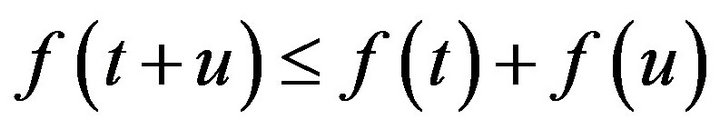 for all
for all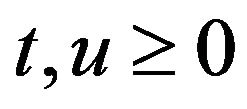 (3)
(3) 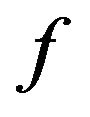 is nondecreasing, and
is nondecreasing, and
(4)  is continuous from the right at zero.
is continuous from the right at zero.
Ruckle [10] used the idea of a modulus function 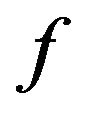 to construct the sequence space
to construct the sequence space
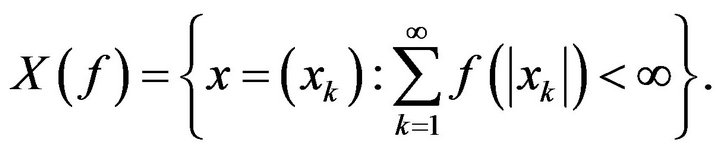
This space is an FK space , and Ruckle[10] proved that the intersection of all such 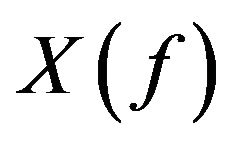 spaces is
spaces is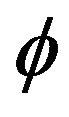 , the space of all finite sequences.
, the space of all finite sequences.
The space X(f) is closely related to the space  which is an X(f) space with
which is an X(f) space with 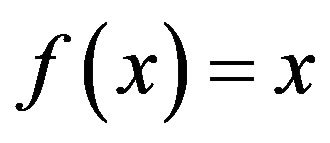 for all real
for all real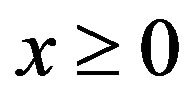 . Thus Ruckle [11] proved that, for any modulus
. Thus Ruckle [11] proved that, for any modulus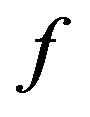 .
.
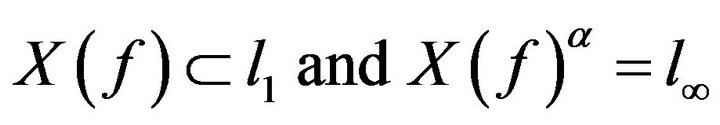
where
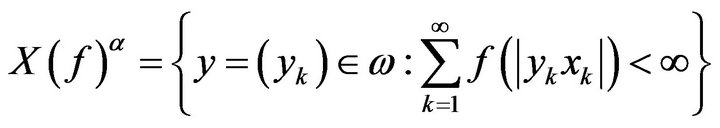
The space  is a Banach space with respect to the norm
is a Banach space with respect to the norm
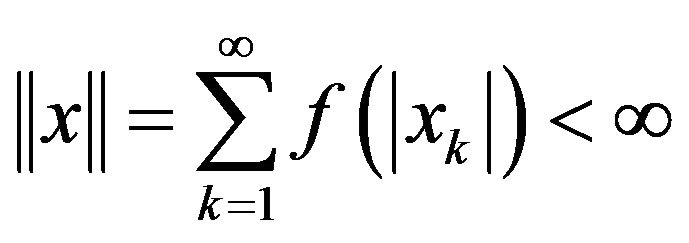 (See [10]).
(See [10]).
Spaces of the type 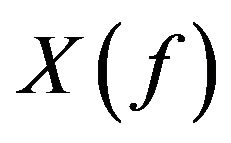 are a special case of the spaces structured by B. Gramsch in [12]. From the point of view of local convexity, spaces of the type
are a special case of the spaces structured by B. Gramsch in [12]. From the point of view of local convexity, spaces of the type 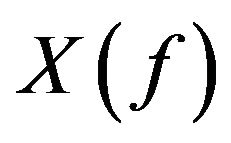 are quite pathological. Therefore symmetric sequence spaces, which are locally convex have been frequently studied by D. J. H. Garling [13,14], G. Kothe [15] and W. H. Ruckle [10,16].
are quite pathological. Therefore symmetric sequence spaces, which are locally convex have been frequently studied by D. J. H. Garling [13,14], G. Kothe [15] and W. H. Ruckle [10,16].
Definition 2.1. A sequence space E is said to be solid or normal if 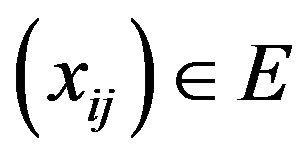 implies
implies 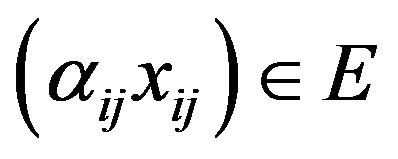 for all sequence of scalars
for all sequence of scalars 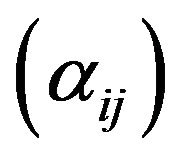 with
with 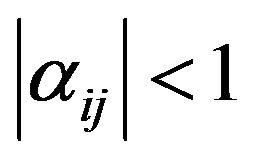 for all
for all 
(see [17])
Definition 2.2. Let

and E be a double sequence space. A 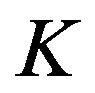 -step space of
-step space of 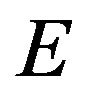 is a sequence space
is a sequence space

Definition 2.3. A cannonical preimage of a sequence 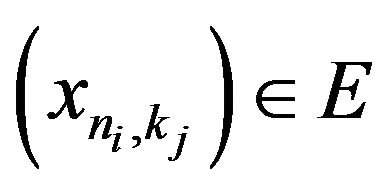 is a sequence
is a sequence 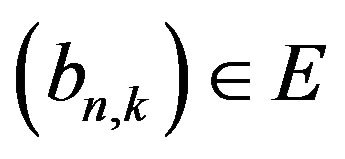 defined as follows
defined as follows
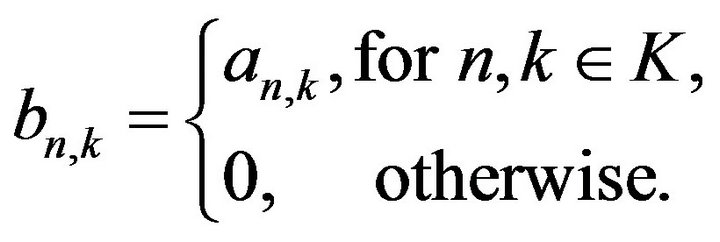 (see [18]).
(see [18]).
Definition 2.4. A sequence space E is said to be monotone if it contains the cannonical preimages of all its stepspaces (see [19]).
Definition 2.5. A sequence space E is said to be convergence free if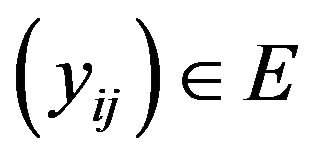 , whenever
, whenever  and
and 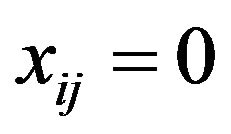 implies
implies .
.
Definition 2.6. A sequence space E is said to be a sequence algebra if 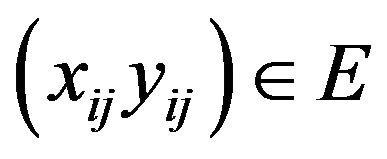 whenever
whenever
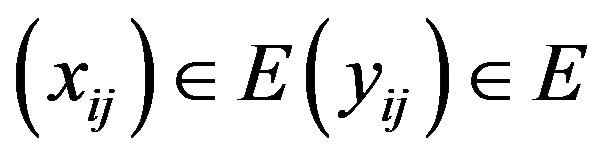 .
.
Definition 2.7. A sequence space E is said to be symmetric if 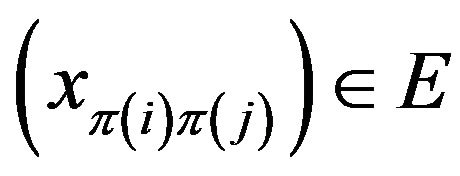 whenever
whenever 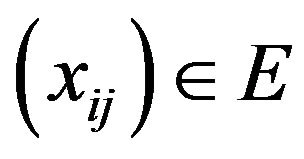 where
where
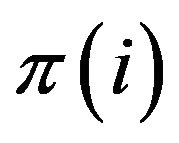 and
and 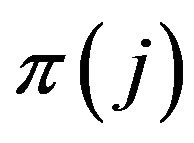 is a permutation on N.
is a permutation on N.
Definition 2.8. A sequence 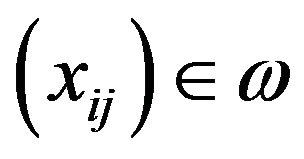 is said to be I-convergent to a number L if for every
is said to be I-convergent to a number L if for every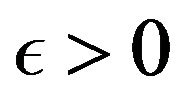 .
.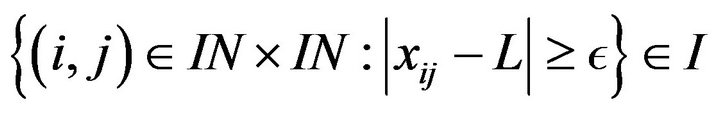 . In this case we write I-lim
. In this case we write I-lim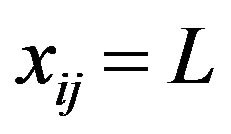 .
.
The space 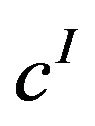 of all I-convergent sequences to
of all I-convergent sequences to ![]() is given by
is given by

Definition 2.9. A sequence 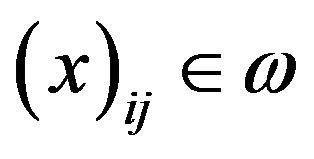 is said to be I-null if
is said to be I-null if . In this case we write I-lim
. In this case we write I-lim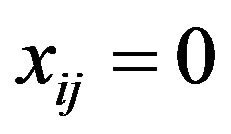 .
.
Definition 2.10. A sequence 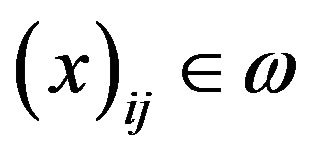 is said to be I-cauchy if for every
is said to be I-cauchy if for every 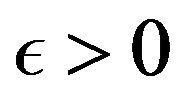 there exists a number
there exists a number 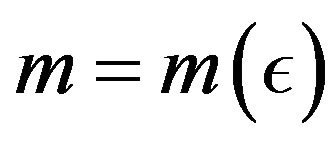 and
and 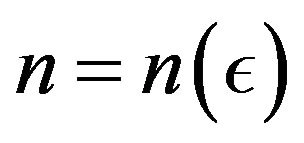 such that
such that
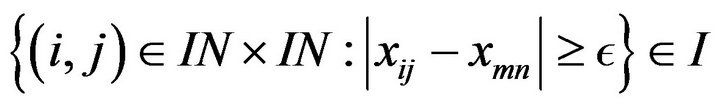 .
.
Definition 2.11. A sequence  is said to be I-bounded if there exists
is said to be I-bounded if there exists 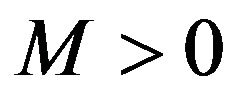 such that
such that
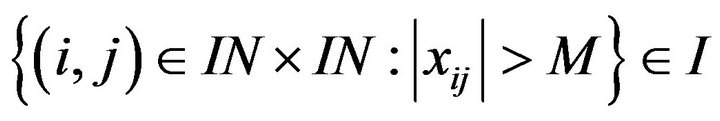
Definition 2.12. A modulus function  is said to satisfy
is said to satisfy 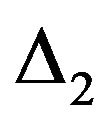 condition if for all values of u there exists a constant
condition if for all values of u there exists a constant 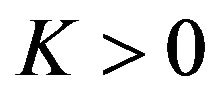 such that
such that 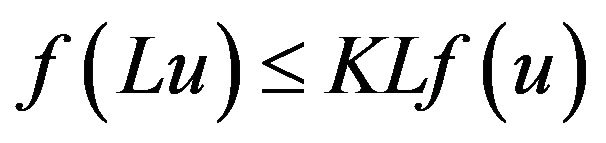 for all values of
for all values of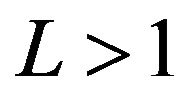 .
.
Definition 2.13. Take for I the class  of all finite subsets of
of all finite subsets of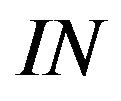 . Then
. Then 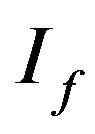 is a non-trivial admissible ideal and
is a non-trivial admissible ideal and 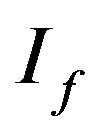 convergence coincides with the usual convergence with respect to the metric in X (see [4]).
convergence coincides with the usual convergence with respect to the metric in X (see [4]).
Definition 2.14. For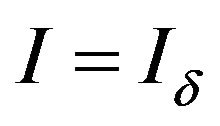 and
and 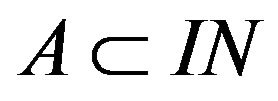 with
with  respectively.
respectively. 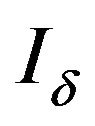 is a non-trivial admissible ideal,
is a non-trivial admissible ideal, 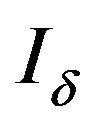 -convergence is said to be logarithmic statistical convergence (see [4]).
-convergence is said to be logarithmic statistical convergence (see [4]).
Definition 2.15. A map  defined on a domain
defined on a domain 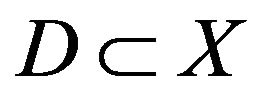 i.e.
i.e.  is said to satisfy Lipschitz condition if
is said to satisfy Lipschitz condition if 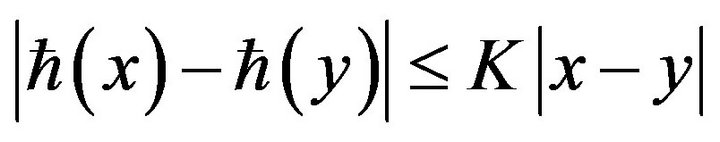 where K is known as the Lipschitz constant. The class of K-Lipschitz functions defined on D is denoted by
where K is known as the Lipschitz constant. The class of K-Lipschitz functions defined on D is denoted by 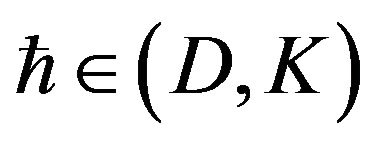 (see [20]).
(see [20]).
Definition 2.16. A convergence field of I-convergence is a set
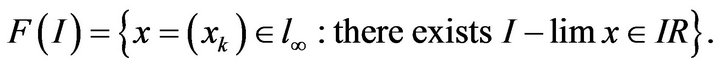
The convergence field 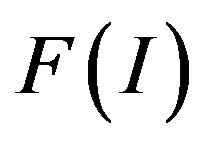 is a closed linear subspace of
is a closed linear subspace of 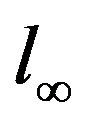 with respect to the supremum norm,
with respect to the supremum norm, 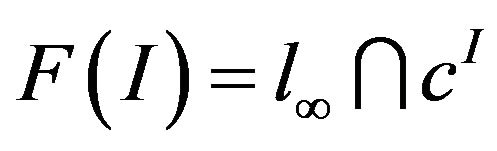 (See [5]).
(See [5]).
Define a function 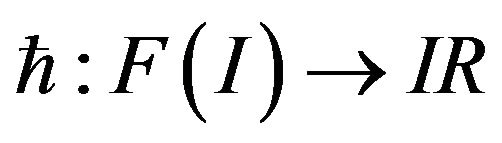 such that
such that
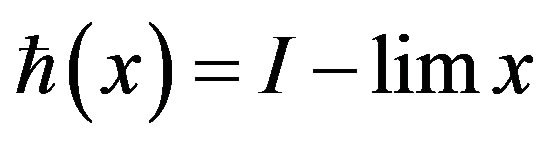 , for all
, for all , then the function
, then the function  is a Lipschitz function (see [20]).
is a Lipschitz function (see [20]).
(c.f [18,20-30])
Throughout the article 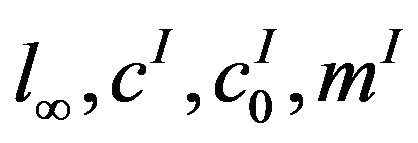 and
and  represent the bounded, I-convergent, I-null, bounded I-convergent and bounded I-null sequence spaces respectively.
represent the bounded, I-convergent, I-null, bounded I-convergent and bounded I-null sequence spaces respectively.
In this article we introduce the following classes of sequence spaces.
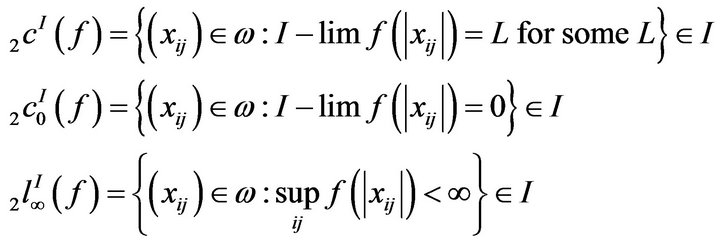
We also denote by
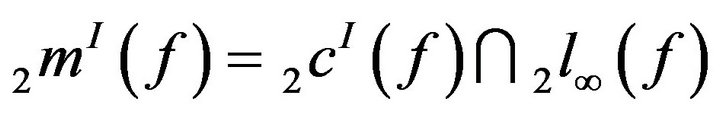
and
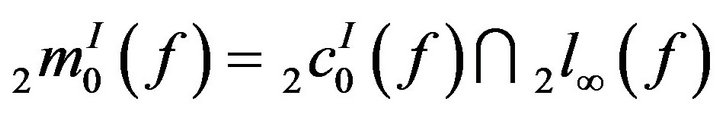
The following Lemmas will be used for establishing some results of this article.
Lemma (1) Let E be a sequence space. If E is solid then E is monotone.
Lemma (2) Let and
and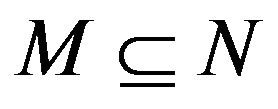 . If
. If , then
, then 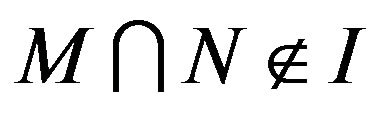
Lemma (3) If 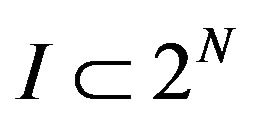 and
and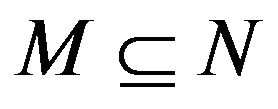 . If
. If , then
, then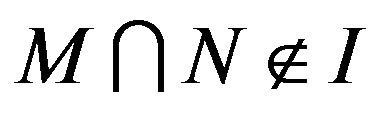 .
.
3. Main Results
Theorem 3.1. For any modulus function f, the classes of sequences  and
and 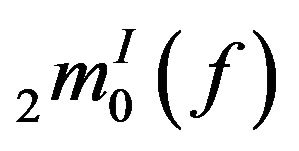 are linear spaces.
are linear spaces.
Proof: We shall prove the result for the space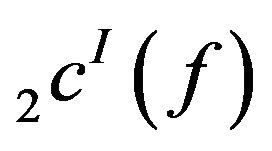 .
.
The proof for the other spaces will follow similarly.
Let  and let
and let 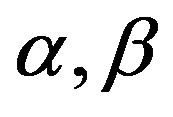 be scalars. Then
be scalars. Then
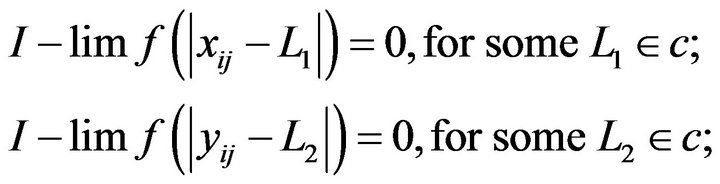
That is for a given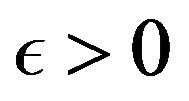 , we have
, we have
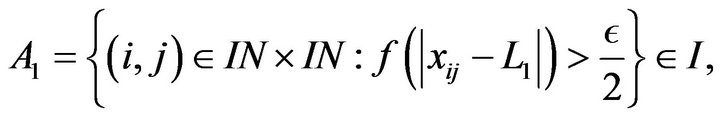 (1)
(1)
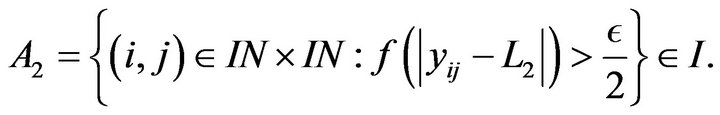 (2)
(2)
Since f is a modulus function, we have
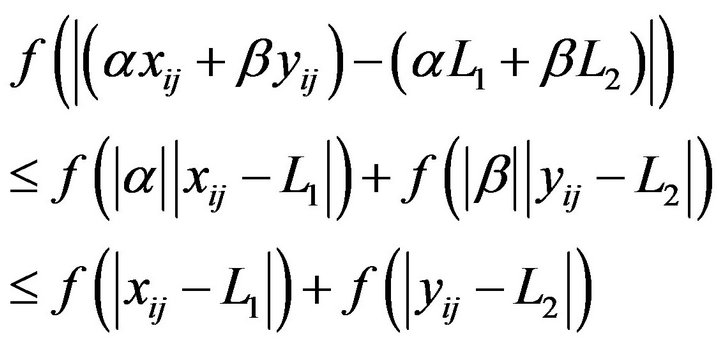
Now, by (1) and (2),
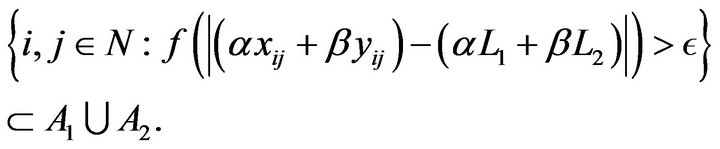
Therefore 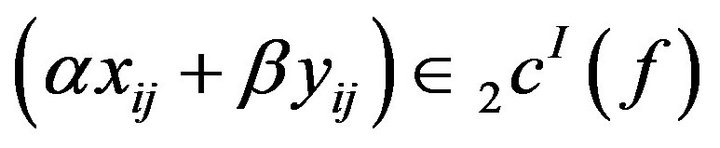
Hence 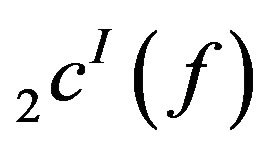 is a linear space.
is a linear space.
Theorem 3.2. A sequence 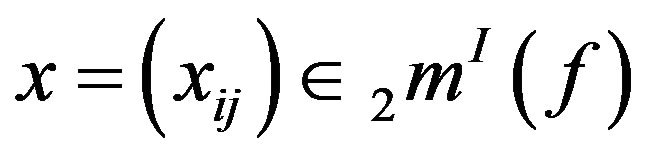 is I-convergent if and only if for every
is I-convergent if and only if for every  there exists
there exists 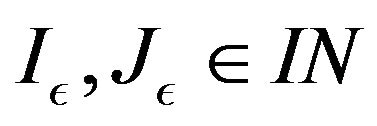 such that
such that
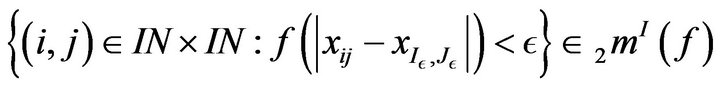 (3)
(3)
Proof: Suppose that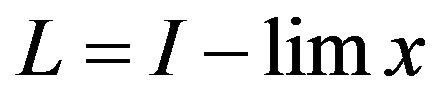 . Then
. Then
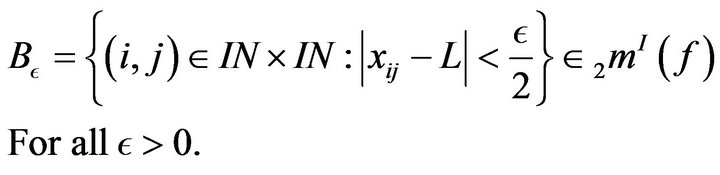
Fix an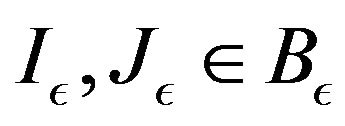 . Then we have
. Then we have

which holds for all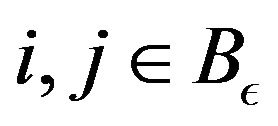 .
.
Hence 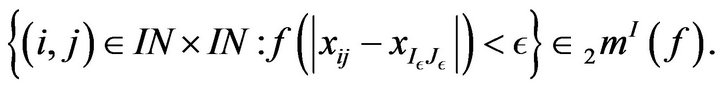
Conversely, suppose that
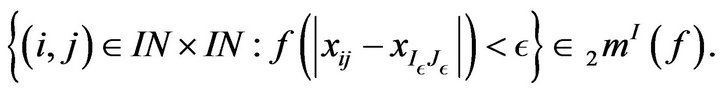
That is 
for all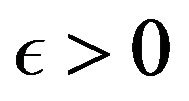 . Then the set
. Then the set
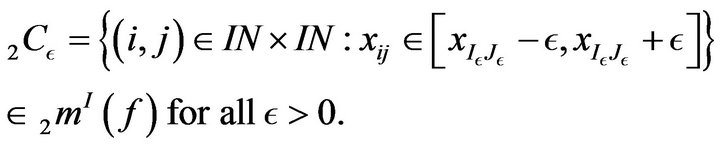
Let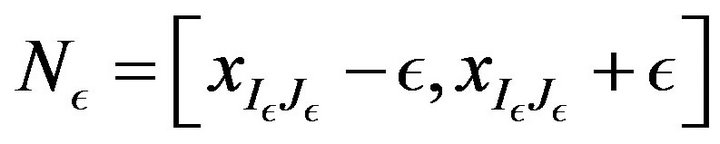 . If we fix an
. If we fix an 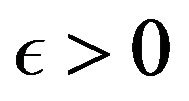 then we have
then we have 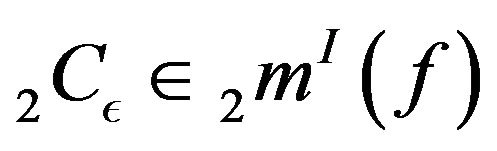 as well as
as well as 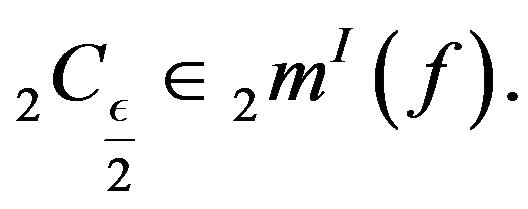
Hence 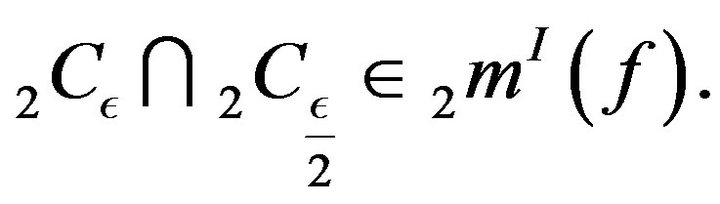 This implies that
This implies that
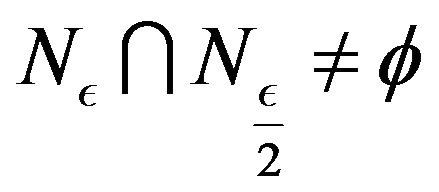
that is
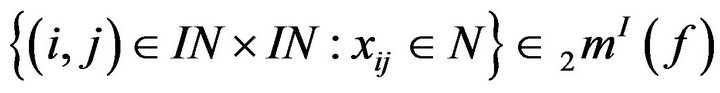
that is
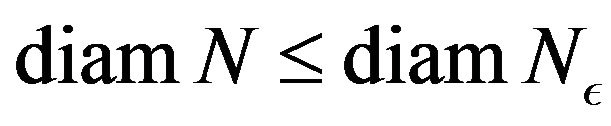
where the diam of N denotes the length of interval N.
In this way, by induction we get the sequence of closed intervals
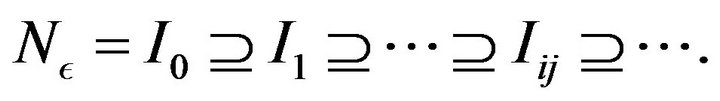
with the property that 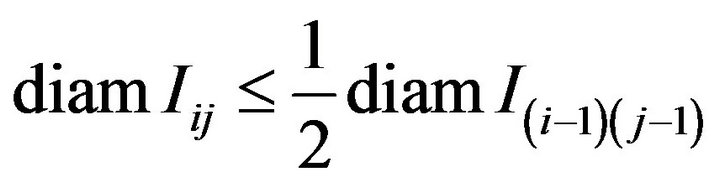 for
for
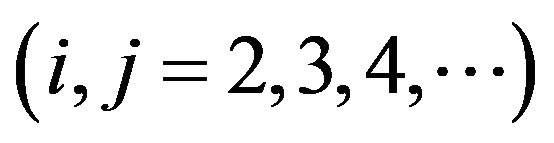 and
and
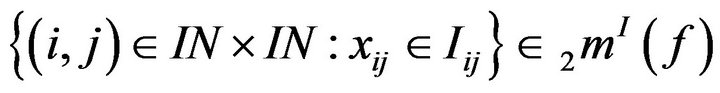 for
for
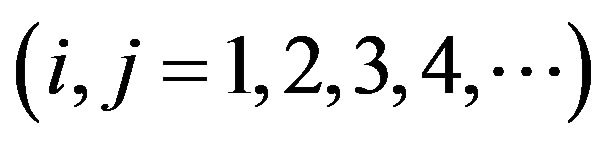 .
.
Then there exists a  where
where 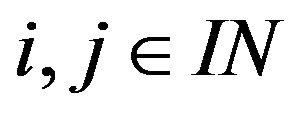 such that
such that . So that
. So that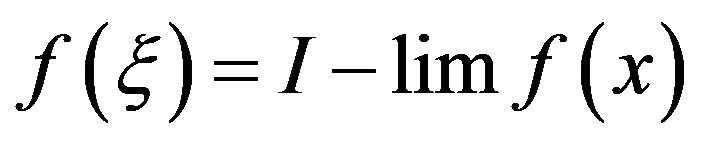 , that is
, that is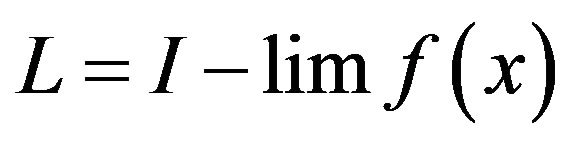 .
.
Theorem 3.3. Let 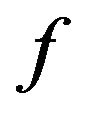 and
and ![]() be modulus functions that satisfy the
be modulus functions that satisfy the 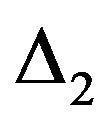 -condition.If
-condition.If 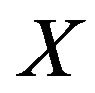 is any of the spaces
is any of the spaces 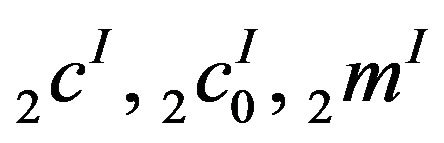 and
and 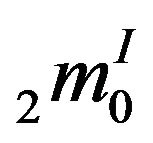 etc, then the following assertions hold.
etc, then the following assertions hold.
(i)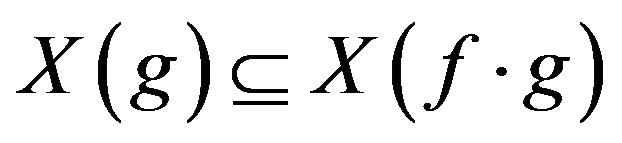 ,
,
(ii)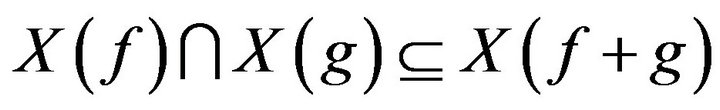 .
.
Proof: (i) Let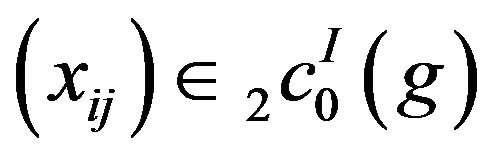 . Then
. Then
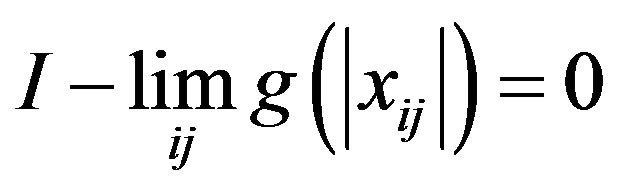 (4)
(4)
Let 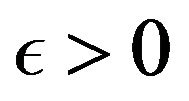 and choose
and choose ![]() with
with  such that
such that 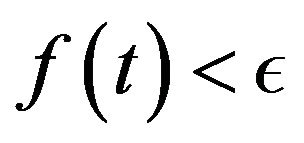 for
for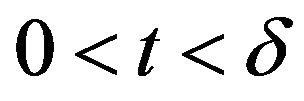 .
.
Write 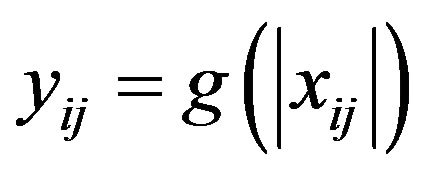 and consider
and consider

We have
 (5)
(5)
For , we have
, we have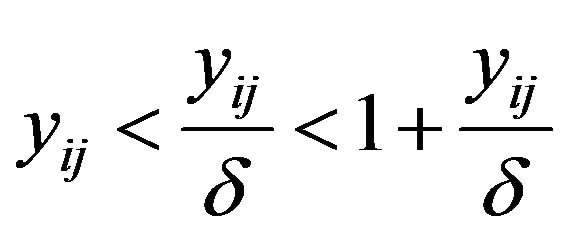 . Since f is non-decreasing,it follows that
. Since f is non-decreasing,it follows that

Since 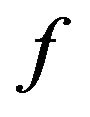 satisfies the
satisfies the  -condition, we have
-condition, we have

Hence
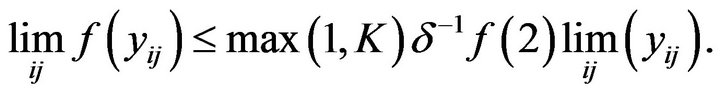 (6)
(6)
From (4), (5) and (6), we have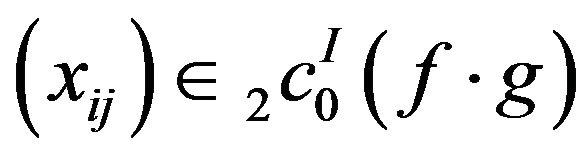 .
.
Thus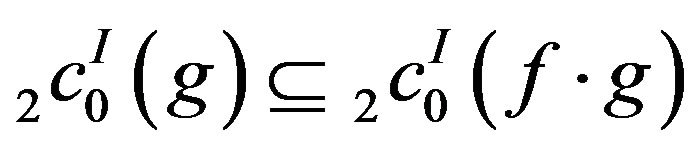 . The other cases can be proved similarly.
. The other cases can be proved similarly.
(ii) Let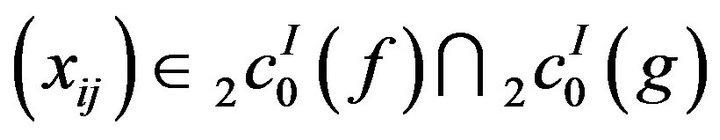 . Then
. Then
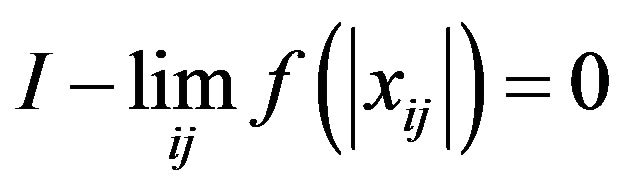 and
and 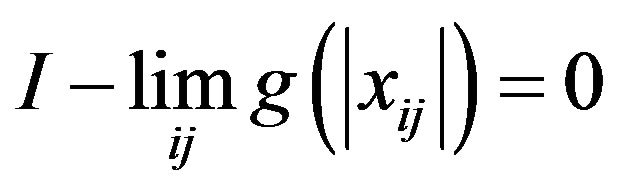

Therefore
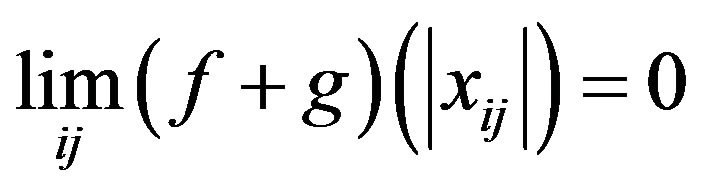
which implies 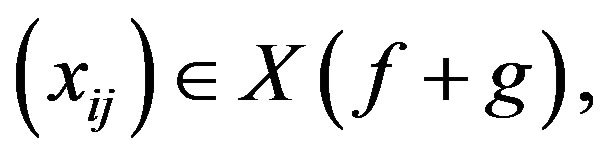 that is
that is

Corollary 3.4.  for
for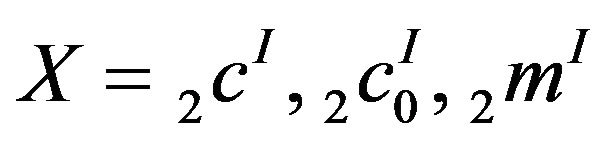 and
and 
Proof: The result can be easily proved using  for
for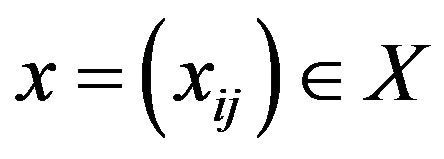 .
.
Theorem 3.5. The spaces 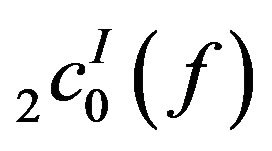 and
and 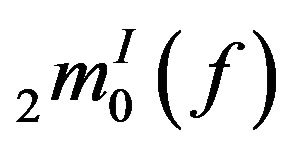 are solid and monotone.
are solid and monotone.
Proof: We shall prove the result for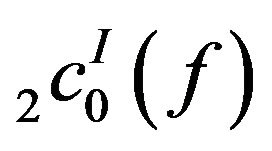 . Let
. Let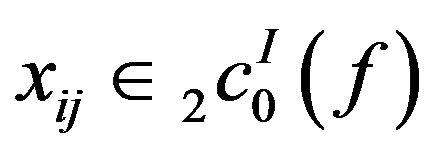 . Then
. Then
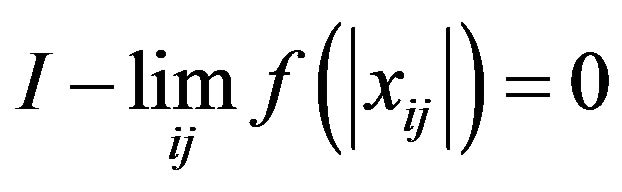 (7)
(7)
Let  be a sequence of scalars with
be a sequence of scalars with 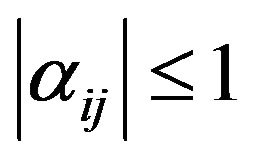 for all
for all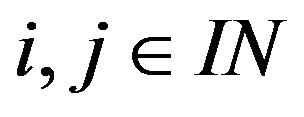 . Then we have
. Then we have
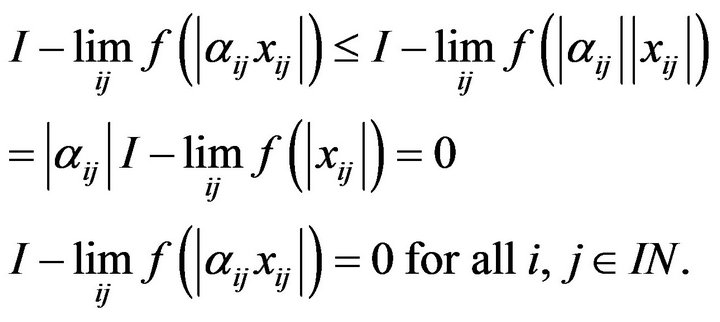
which implies that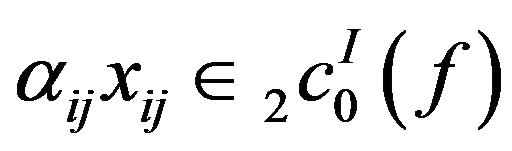 .
.
Therefore the space 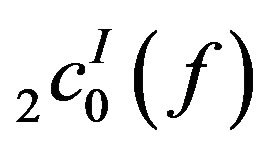 is solid. The space
is solid. The space
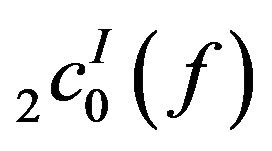 is monotone follows from Lemma (1). For
is monotone follows from Lemma (1). For
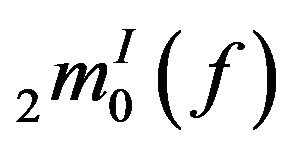 the result can be proved similarly.
the result can be proved similarly.
Theorem 3.6. The spaces 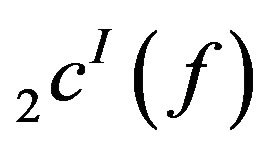 and
and 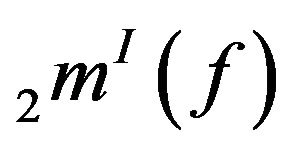 are neither solid nor monotone in general.
are neither solid nor monotone in general.
Proof: Here we give a counter example.
Let 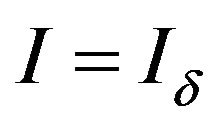 and
and 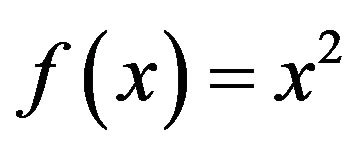 for all
for all 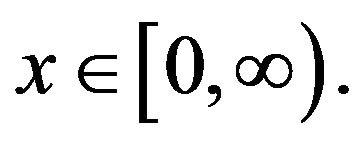 Consider the K-step space
Consider the K-step space 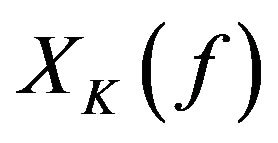 of X defined as follows, Let
of X defined as follows, Let 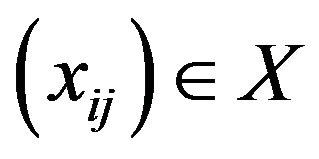 and let
and let 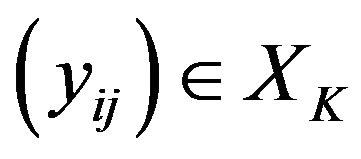 be such that
be such that
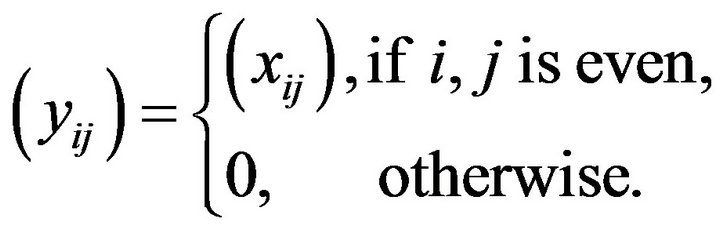
Consider the sequence 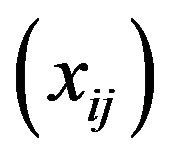 defined by
defined by 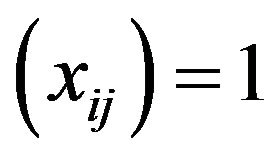 for all
for all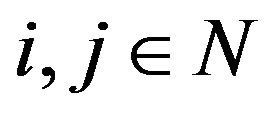 .
.
Then 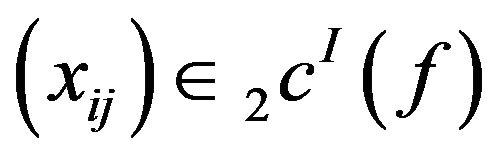 but its K-stepspace preimage does not belong to
but its K-stepspace preimage does not belong to 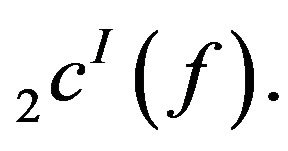 Thus
Thus 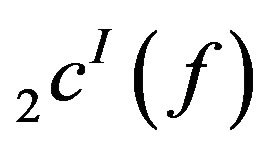 is not monotone. Hence
is not monotone. Hence 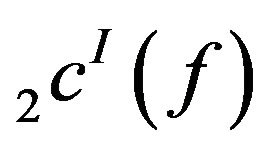 is not solid.
is not solid.
Theorem 3.7. The spaces 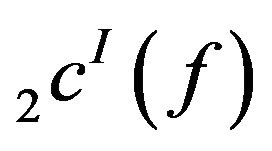 and
and  are sequence algebras.
are sequence algebras.
Proof: We prove that  is a sequence algebra.
is a sequence algebra.
Let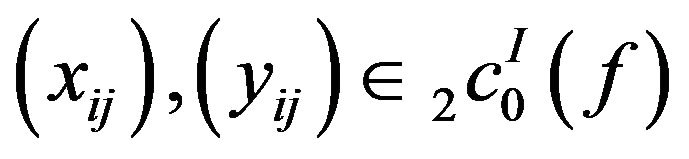 . Then
. Then
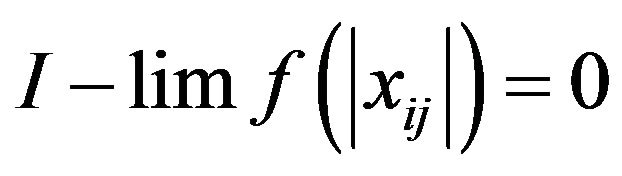
and
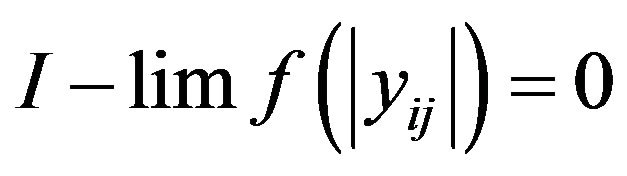
Then we have
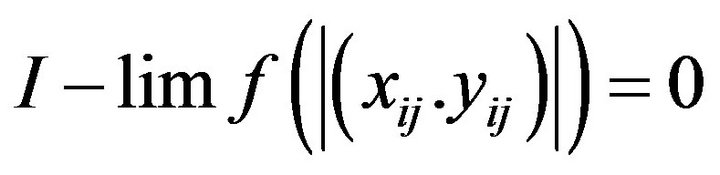
Thus 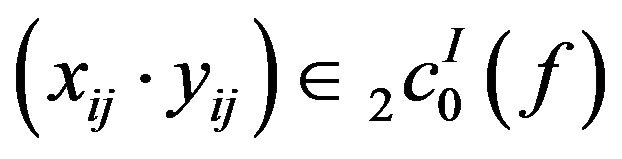 is a sequence algebra.
is a sequence algebra.
For the space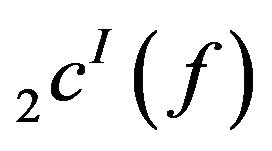 , the result can be proved similarly.
, the result can be proved similarly.
Theorem 3.8. The spaces 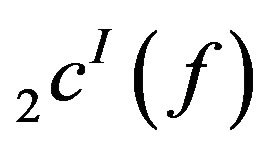 and
and  are not convergence free in general.
are not convergence free in general.
Proof: Here we give a counter example.
Let 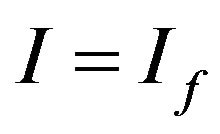 and
and 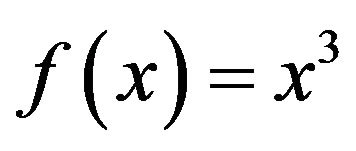 for all
for all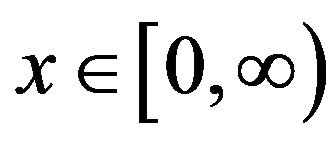 . Consider the sequence
. Consider the sequence 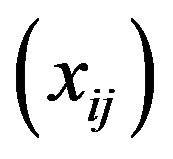 and
and 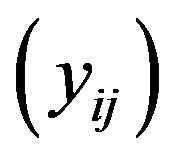 defined by
defined by
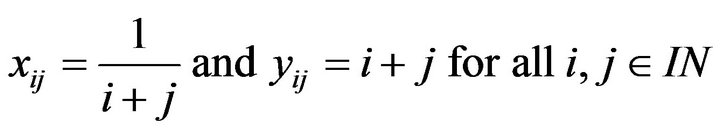
Then 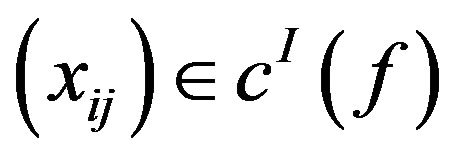 and
and , but
, but 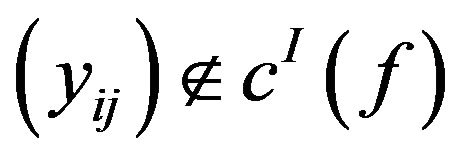
and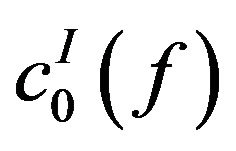 .
.
Hence the spaces  and
and 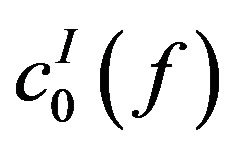 are not convergence free.
are not convergence free.
Theorem 3.9. If I is not maximal and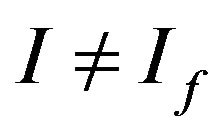 , then the spaces
, then the spaces 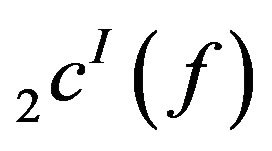 and
and 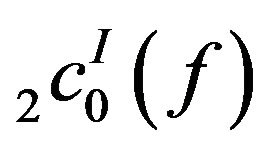 are not symmetric.
are not symmetric.
Proof: Let  be infinite and
be infinite and 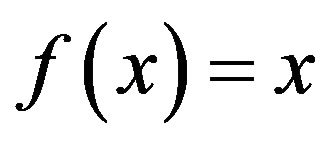 for all
for all 
If
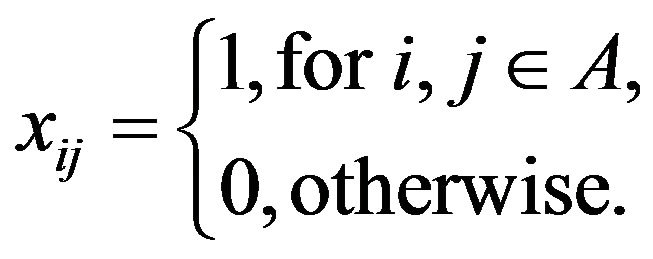
Then by Lemma (3) we have .
.
Let  be such that
be such that  and
and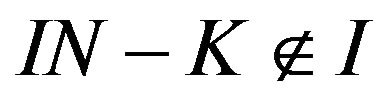 .
.
Let 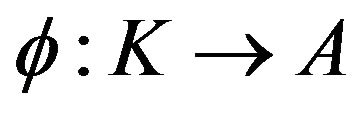 and
and 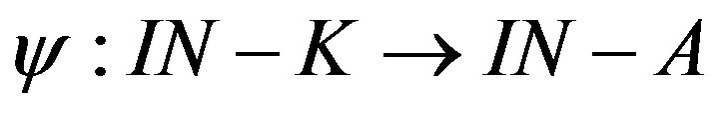 be bijections, then the map
be bijections, then the map 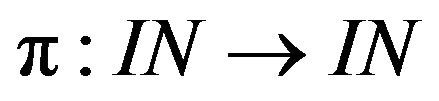 defined by
defined by
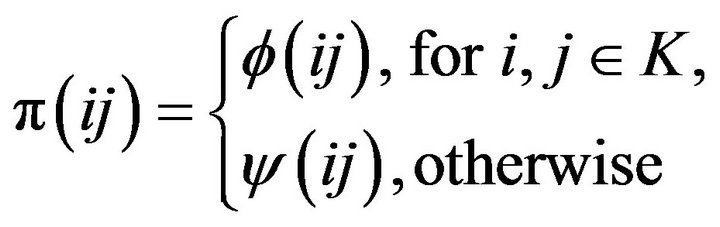
is a permutation on , but
, but 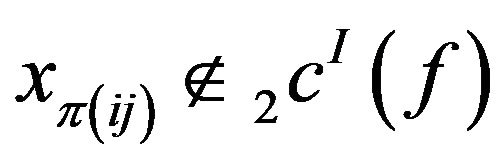 and
and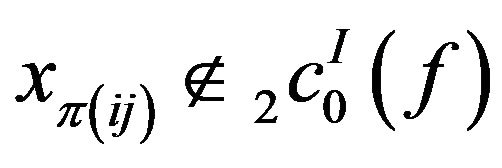 .
.
Hence 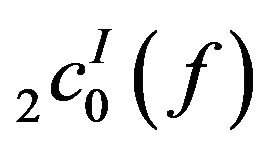 and
and 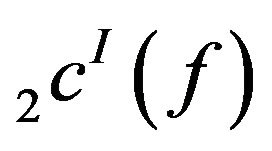 are not symmetric.
are not symmetric.
Theorem 3.10. Let f be a modulus function. Then 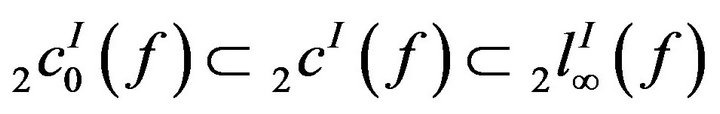 and the inclusions are proper.
and the inclusions are proper.
Proof: The inclusion 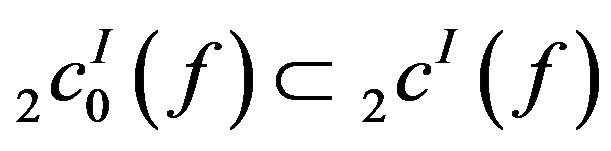 is obvious.
is obvious.
Let 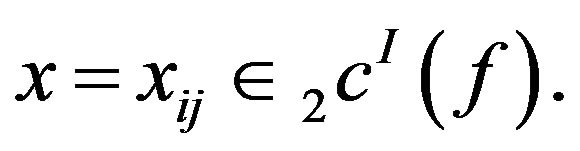 Then there exists
Then there exists 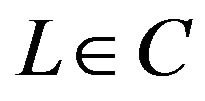 such that
such that
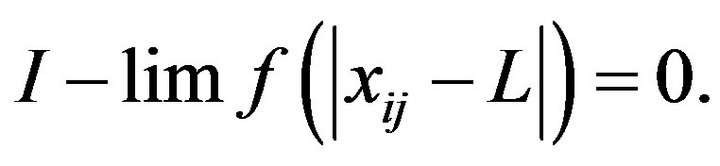
We have 
Taking the supremum over  on both sides we get
on both sides we get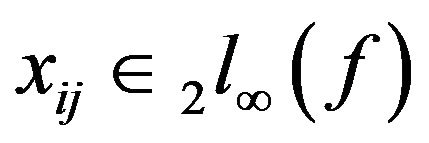 .
.
Next we show that the inclusion is proper.
(i) 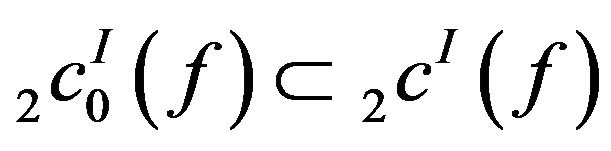
Let 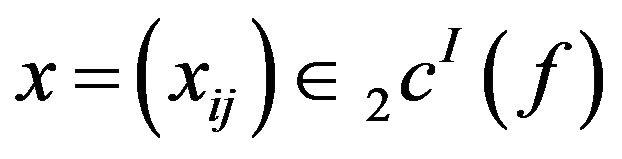 then
then 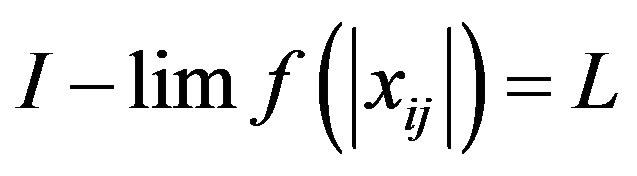 for some
for some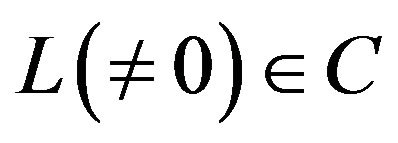 , which implies
, which implies 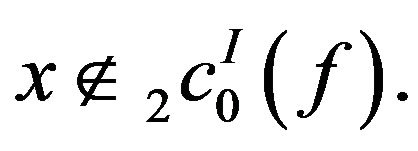 Hence the inclusion is proper.
Hence the inclusion is proper.
(ii)  Let
Let 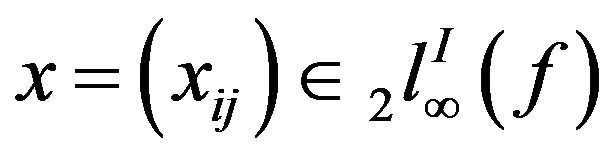 then
then

Therefore , and hence the inclusion is proper.
, and hence the inclusion is proper.
Theorem 3.11. The function 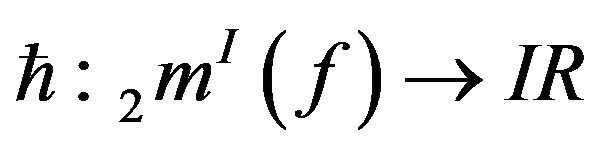 is the Lipschitz function, where
is the Lipschitz function, where
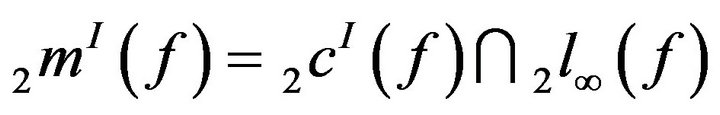 , and hence uniformly continuous.
, and hence uniformly continuous.
Proof: Let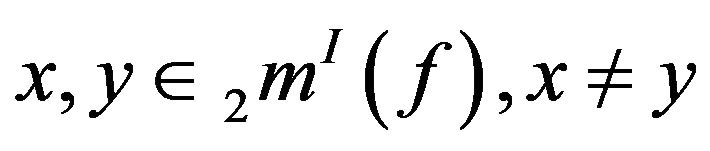 . Then the sets
. Then the sets
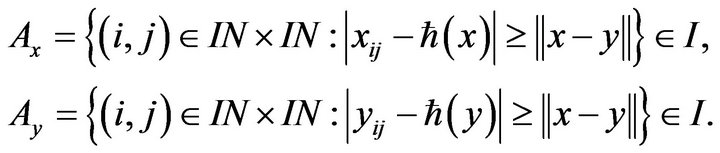
Thus the sets,
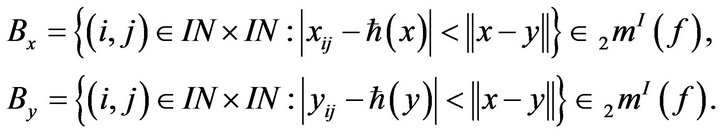
Hence also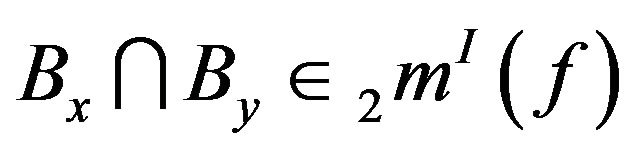 , so that
, so that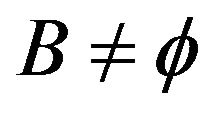 .
.
Now taking 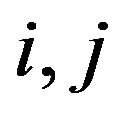 in
in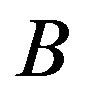 ,
,

Thus  is a Lipschitz function. For
is a Lipschitz function. For 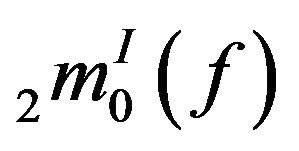 the result can be proved similarly.
the result can be proved similarly.
Theorem 3.12. If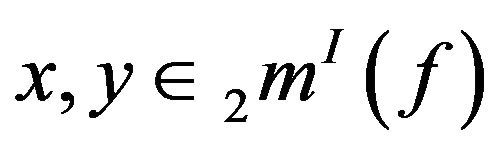 , then
, then
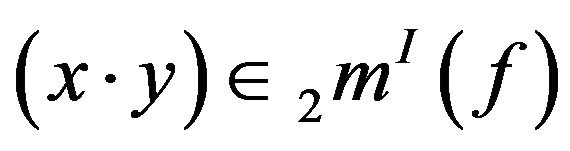 and
and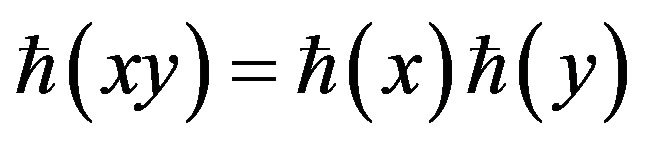 .
.
Proof: For 
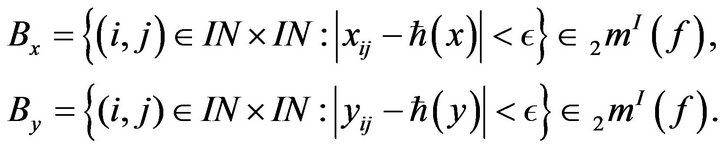
Now,
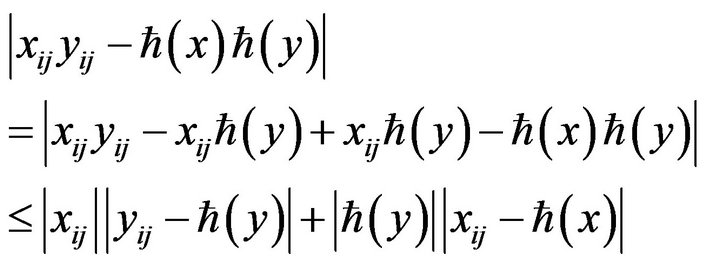 (8)
(8)
As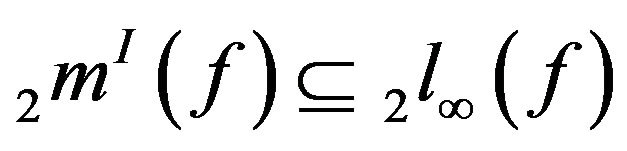 , there exists an
, there exists an 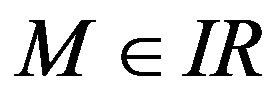 such that
such that 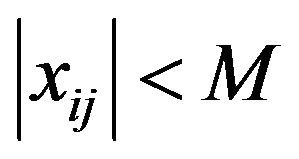 and
and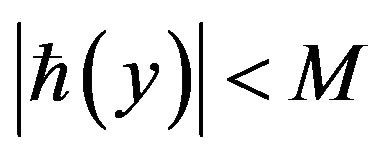 .
.
Using Equation (8) we get
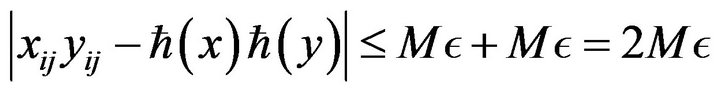
For all . Hence
. Hence
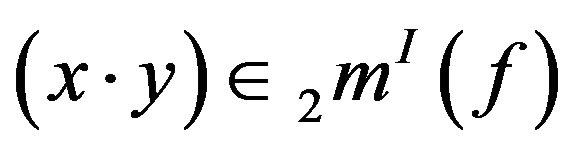 and
and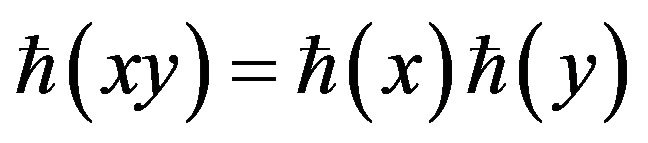 .
.
For 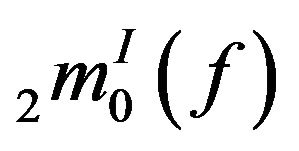 the result can be proved similarly.
the result can be proved similarly.
4. Acknowledgements
The authors would like to record their gratitude to the reviewer for his careful reading and making some useful corrections which improved the presentation of the paper.
REFERENCES
- H. Fast, “Sur la Convergence Statistique,” Colloqium Mathematicum, Vol. 2, No. 1, 1951, pp. 241-244.
- J. A. Fridy, “On Statistical Convergence,” Analysis, Vol. 5, 1985, pp. 301-313.
- J. A. Fridy, “Statistical Limit Points,” Proceedings of American Mathematical Society, Vol. 11, 1993, pp. 1187- 1192. doi:10.1090/S0002-9939-1993-1181163-6
- P. Kostyrko, T. Salat and W. Wilczynski, “I-Convergence,” Real Analysis Exchange, Vol. 26, No. 2, 1999, pp. 193-200.
- T. Salat, B. C. Tripathy and M. Ziman, “On Some Properties of I-Convergence,” Tatra Mountain Mathematical Publications, 2000, pp. 669-686.
- K. Demirci, “I-Limit Superior and Limit Inferior,” Mathematical Communications, Vol. 6, 2001, pp. 165-172.
- T. J. I. Bromwich, “An Introduction to the Theory of Infinite Series,” MacMillan Co. Ltd., New York, 1965.
- M. Basarir and O. Solancan, “On Some Double Sequence Spaces,” Journal of the Indian Academy of Mathematics, Vol. 21, No. 2, 1999, pp. 193-200.
- H. Nakano, “Concave Modulars,” Journal of Mathematical Society, Japan, Vol. 5, No. 1, 1953, pp. 29-49. doi:10.2969/jmsj/00510029
- W. H. Ruckle, “On Perfect Symmetric BK-Spaces,” Mathematische Annalen, Vol. 175, No. 2, 1968, pp. 121-126. doi:10.1007/BF01418767
- W. H. Ruckle, “FK-Spaces in Which the Sequence of Coordinate Vectors is Bounded,” Canadian Journal of Mathematics, Vol. 25, No. 5, 1973, pp. 973-975. doi:10.4153/CJM-1973-102-9
- B. Gramsch, “Die Klasse Metrisher Linearer Raume L(φ),” Mathematische Annalen, Vol. 171, 1967, pp. 61- 78. doi:10.1007/BF01433094
- D. J. H. Garling, “On Symmetric Sequence Spaces,” Proceedings of London Mathematical Society, Vol. 16, 1966, pp. 85-106. doi:10.1112/plms/s3-16.1.85
- D. J. H. Garling, “Symmetric Bases of Locally Convex Spaces,” Studia Mathematica, Vol. 30, No. 2, 1968, pp. 163-181.
- G. Kothe, “Topological Vector Spaces,” Springer, Berlin, 1970.
- W. H. Ruckle, “Symmetric Coordinate Spaces and Symmetric Bases,” Canadian Journal of Mathematics, Vol. 19, 1967, pp. 828-838. doi:10.4153/CJM-1967-077-9
- V. A. Khan and S. Tabassum, “On Some New Double Sequence Spaces of Invariant Means Defined by Orlicz Function,” Communications, Faculty of Sciences, University of Ankara, Vol. 60, 2011, pp. 11-21.
- J. Singer, “Bases in Banach Spaces. 1,” Springer, Berlin, 1970.
- M. Sen and S. Roy, “Some I-Convergent Double Classes of Sequences of Fuzzy Numbers Defined by Orlicz Functions,” Thai Journal of Mathematics, Vol. 10, No. 4, 2013, pp. 1-10.
- I. J. Maddox, “Some Properties of Paranormed Sequence Spaces,” Journal of the London Mathematical Society, Vol. 1, 1969, pp. 316-322.
- J. Connor and J. Kline, “On Statistical Limit Points and the Consistency of Statistical Convergence,” Journal of Mathematical Analysis and Applications, Vol. 197, No. 2, 1996, pp. 392-399. doi:10.1006/jmaa.1996.0027
- K. Dems, “On I-Cauchy Sequences,” Real Analysis Exchange, Vol. 30, No. 1, 2005, pp. 123-128.
- M. Gurdal, “Some Types Of Convergence,” Doctoral Dissertation, Sleyman Demirel University, Isparta, 2004.
- O. T. Jones and J. R. Retherford, “On Similar Bases in Barrelled Spaces,” Proceedings of American Mathematical Society, Vol. 18, 1967, pp. 677-680. doi:10.1090/S0002-9939-1967-0217552-8
- P. K. Kamthan and M. Gupta, “Sequence Spaces and Series,” Marcel Dekker Inc., New York, 1981.
- I. J. Maddox, “Elements of Functional Analysis,” Cambridge University Press, Cambridge, 1970.
- I. J. Maddox, “Sequence Spaces Defined by a Modulus,” Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 100, 1986, pp. 161-166. doi:10.1017/S0305004100065968
- T. Salat, “On Statistically Convergent Sequences of Real Numbers,” Mathematica Slovaca, Vol. 30, 1980, pp. 139- 150.
- A. K. Vakeel and K. Ebadullah, “On Some I-Convergent Sequence Spaces Defined by a Modulus Function,” Theory and Applications of Mathematics and Computer Science, Vol. 1, No. 2, 2011, pp. 22-30.
- A. Wilansky, “Functional Analysis,” Blaisdell, New York, 1964.

