Engineering
Vol.5 No.5(2013), Article ID:31699,6 pages DOI:10.4236/eng.2013.55060
Approximate Analytical Solution to Temperature Profile in a Solid Composite Heated by a Pulsed Laser
1Department of Physics, Faculty of Science, Universiti Putra Malaysia, Serdang, Malaysia
2Department of Mathematics, Faculty of Science, Universiti Putra Malaysia, Serdang, Malaysia
Email: *maarof@science.upm.edu.my
Copyright © 2013 Sani Jibrin et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 12, 2013; revised March 21, 2013; accepted March 28, 2013
Keywords: Laplace Transforms; Subsidiary Equations; Laplace Inversion Theorem; Laser Pulse
ABSTRACT
The flash technique of thermal diffusivity measurement applied to composite materials is dependent upon the success at deriving and solving the associated heat diffusion equation for the particular boundary problems of the experiment. Orthogonal expansion technique and the Green’s function approach are easier and straight forward for deriving and solving such equations, but the solutions converge very slowly for small times and hence cannot be used for numerical calculations. The Laplace transformation technique on the other hand has advantage of allowing for the making of small time approximation in order to obtain solutions that are very rapidly convergent. The principle difficulty of this technique is in the inversion of the resulting transform from s to t domain. Inversion by contour integration requires a lot of mastery in integral calculus and the simplest method is therefore to look up for the transform in the standard Laplace conversion table. At first look not all subsidiary equations can be converted using the Laplace transform conversion table; in this work however, we present the mathematical analysis by means of which analytical solutions to heat diffusion problem in composite media; hitherto only transformed via contour integration, is obtained directly from the Laplace transform conversion tables.
1. Introduction
The flash technique of thermal diffusivity measurements introduced by Parker et al. [1] in 1960 is so easy and successful that it can be extended to composite materials. Larson and Koyama [2] published the first detail work on the mathematical formulation of composite material for thermal diffusivity experiments. The analysis they presented allows the measurements of thermo-physical properties of materials to be made for the material in one of the layers if the corresponding values are known for the materials in the second layer. El-Adawi et al. [3] studied the laser heating of two layer system using the Laplace integral transform method and obtained the expression for the temperature profiles in the thin film and the substrate. Jannot et al. [4] presents a new method dedicated to thermal conductivity measurement of low density insulating materials consisting of three layers experimental device. Macmaster and Dinwiddie [5] developed an analytical method for determining the thermal conductivity of a thin film on a substrate of known thermal properties using the flash diffusivity method. Their research examined the effect of inaccuracies in the known parameters on the estimation of the thermal conductivity of the film. Balageas et al. [6] presented exact analytical solutions of the heat diffusion problem encountered in the pulsed photothermal evaluation of two and three layered materials with imperfect interfaces. Their model provides a new method of measuring the quality of the interface. Abd El-Ghany [7] examined the problem of temperature distribution in a three-layer plate heated by a laser pulse. Hui and Tan [8] proposed a photothermal pulse method to determine the in-plane thermal diffusivity of thin films using a point source excitation. They extensively used Laplace transformation technique to derive the inverse temperature profile in a single layer and composite consisting of two, three, 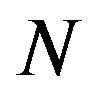 , and
, and 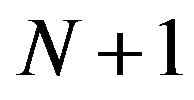 layers.
layers.
Ozisik [9] in his book devoted a chapter for the mathematical analysis of heat conduction in a one-dimensional composite medium. In this book, three analytical methods namely: Laplace transform, Green’s function and orthogonal expansions techniques have been discussed. The orthogonal expansion technique and the Green’s function approach are understood to be easier and straight forward for solving heat diffusion problems, but the solutions converge very slowly for small times. The Laplace transformation on the other hand has the advantage of allowing for the making of small time approximation in order to obtain solutions that are very rapidly convergent. Jaeger [10] in his book set aside three different chapters for Laplace transform technique of solving different heat diffusion problems.
In this work we present the mathematical analysis by means of which analytical solutions to heat diffusion problem in composite media can be obtained directly from the Laplace transform conversion tables as opposed to the complicated integral Laplace inversion theorem.
2. Formulation of the Problem
The mathematical arrangements for the laser heating of the front surface of a composite sample while monitoring the temperature-time history of the rear or front face have been described by several researchers [2-7,11-13] hence; only a brief description of the problem is given here. We consider the first semi-infinite region 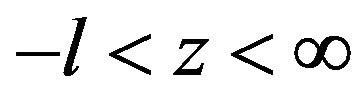 of which
of which 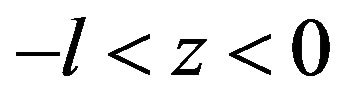 is of one medium (layer 1) and
is of one medium (layer 1) and 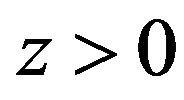 is of another medium (layer 2). We further write
is of another medium (layer 2). We further write 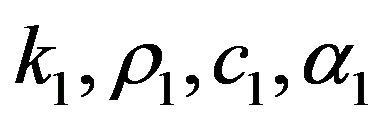 and
and ![]() for thermal conductivity, density, specific heat capacity, thermal diffusivity and temperature in the region
for thermal conductivity, density, specific heat capacity, thermal diffusivity and temperature in the region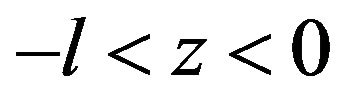 , and
, and 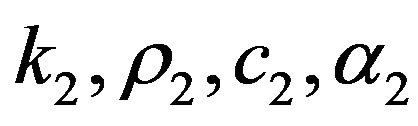 and
and 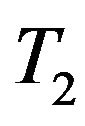 for the corresponding quantities in
for the corresponding quantities in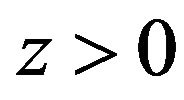 . At time
. At time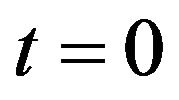 , when the system is in thermal equilibrium with ambient temperature
, when the system is in thermal equilibrium with ambient temperature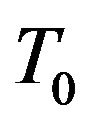 , an intense heat pulse from the laser source is incident, absorbed and subsequently transported axially and radially from the front surface. In this work, it is only the temperature excursion above
, an intense heat pulse from the laser source is incident, absorbed and subsequently transported axially and radially from the front surface. In this work, it is only the temperature excursion above 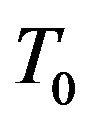 recorded at the rear surface which is of interest. It is assumed in this kind of arrangement that as the temperature excursion is very small all thermo-physical properties of the sample will retain their normal values as at
recorded at the rear surface which is of interest. It is assumed in this kind of arrangement that as the temperature excursion is very small all thermo-physical properties of the sample will retain their normal values as at . In addition, it is also assumed that there exists a perfect thermal interface between the two layers under considerations. We consider the linear heat conduction equation to be solved as
. In addition, it is also assumed that there exists a perfect thermal interface between the two layers under considerations. We consider the linear heat conduction equation to be solved as
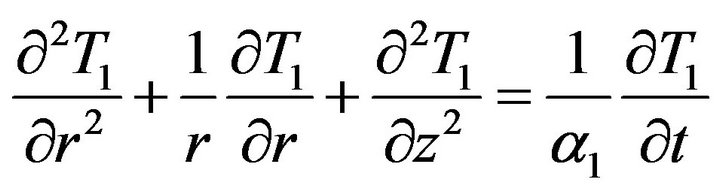 (1)
(1)
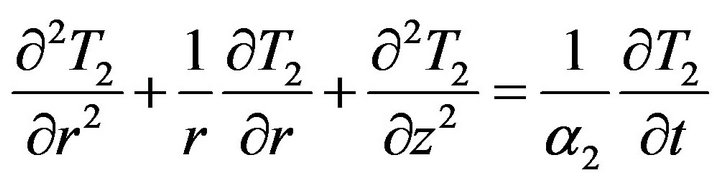 (2)
(2)
For layers 1 and 2 respectively The corresponding initial conditions for Equations (1) and (2) are
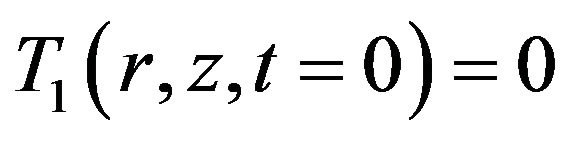 (3)
(3)
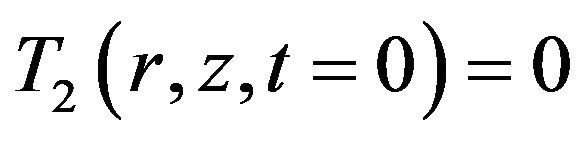 (4)
(4)
The boundary conditions for perfect thermal interface are given as
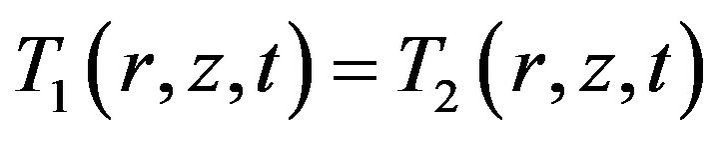 (5)
(5)
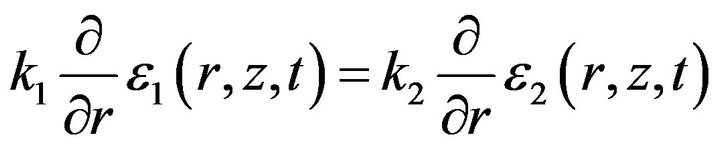 (6)
(6)
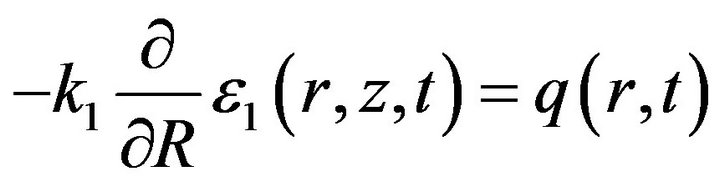 (7)
(7)
where 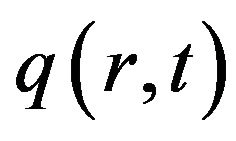 is the input energy flux, and, if the heating is done by a focused laser beam, the spatial–temporal dependence of the heat flux
is the input energy flux, and, if the heating is done by a focused laser beam, the spatial–temporal dependence of the heat flux 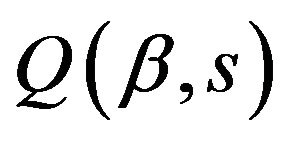 is by [8] expressed as
is by [8] expressed as
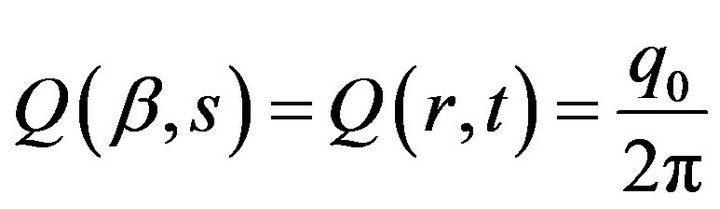 (8)
(8)
Applying the Laplace transform integration technique as done by various researchers [2-10] to Equations (1)-(8) yields
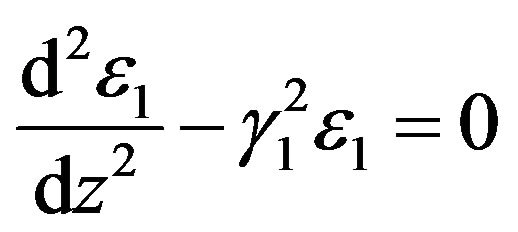 (9)
(9)
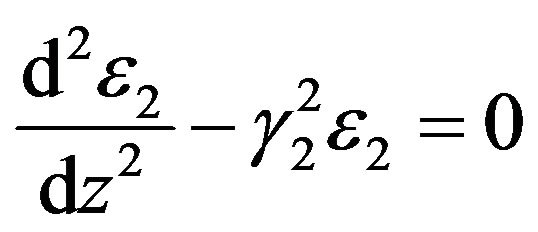 (10)
(10)
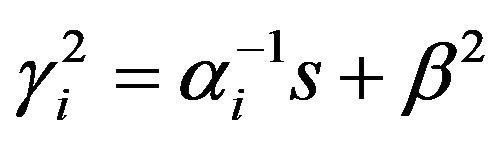 (11)
(11)
where 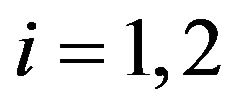 for the two layers respectively.
for the two layers respectively.
The general solution to Equations (9)-(11) together with their boundary and regularity conditions is by [8] written as
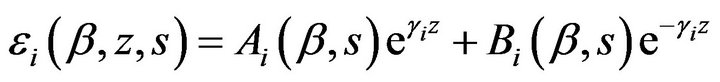 (12)
(12)
where, the coefficients of Ai and Bi are arbitrary integral constants that can be determined by solving the linear algebraic equations from the boundary and regularity conditions.
3. Single Layer Model with Adiabatic Boundary Conditions
Considering the simplest case in which the heat pulse is deposited on the surface of a single-layer solid sample with adiabatic boundary conditions on both surfaces; after dropping the subscripts, Equation (12) becomes
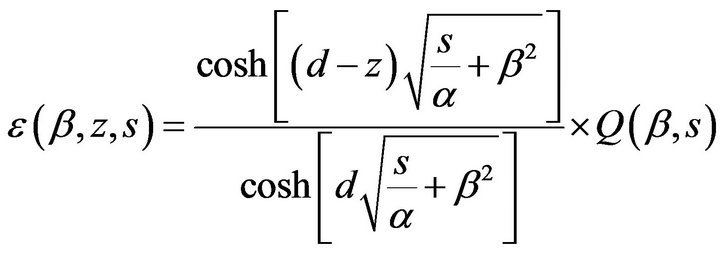 (13)
(13)
Equation (13) is atypical heat conduction problem for finite regions such as slabs and cylinders of finite radius. Such equations are always in a form of a series which converge rapidly for large values of t but converge very slowly for small values of t and hence not suitable for numerical computations for very small values of times [10].
It is vital to mention that whenever the Laplace transform is applied to the time variable it always transforms the equation in t into an equation in s. It is therefore necessary to examine the values of t in the time domain with the corresponding values of s in the Laplace domain. This fact is utilized in obtaining an approximate solution for the function in Equation (13) valid for small times from the knowledge of its transform evaluated for large values of s as done by various researchers [10-13]. Thisrequires that, the transform of the function be expanded as an asymptotic series and then inverted term by term using the Laplace conversion table.
Recall that,
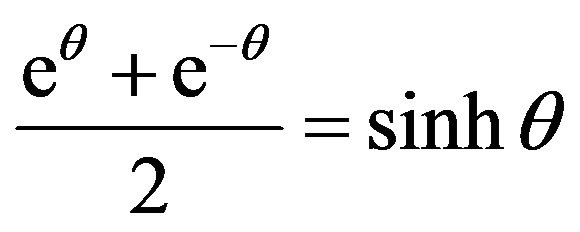 (14)
(14)
and
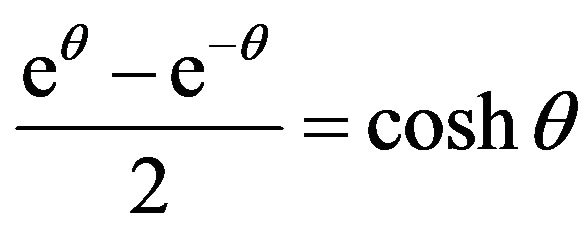 (15)
(15)
Equation (13) can be rewritten as
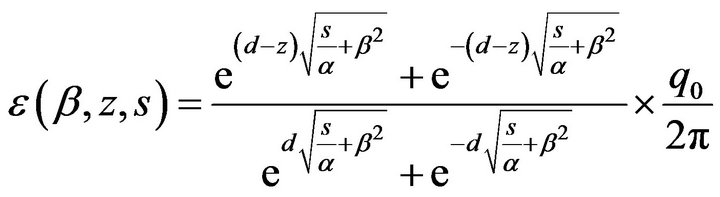
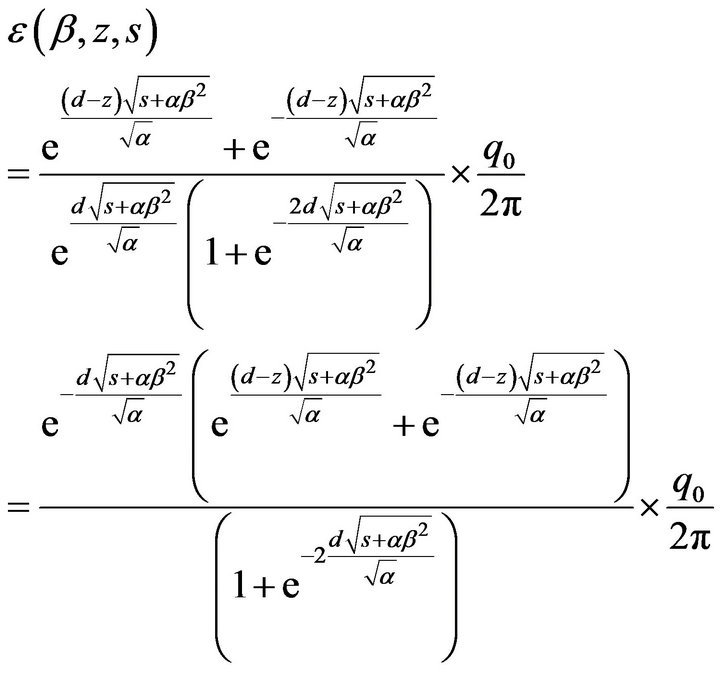
After rearranging and using binomial series expansion we get,
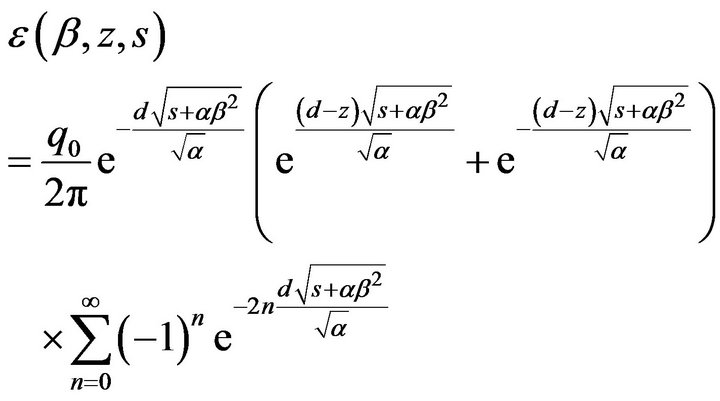
or
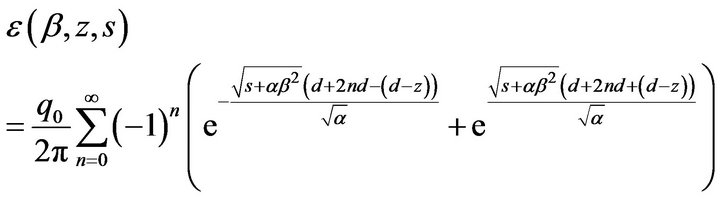 (16)
(16)
where  is the modified Bessel function of the second kind.
is the modified Bessel function of the second kind.
Equation (16) is easily converted to t domain using the Laplace transform conversion table [9, pp. 268-271, Rule 41] with slight modifications as,
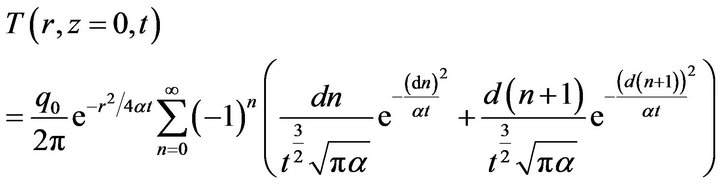 (17)
(17)
Equation (17) converges rapidly for small values of t. It is also to be noted that, this form is often more useful than those obtained by integral inversion theorem, especially for small values of time [10].
4. Two-Layer Films with Adiabatic Boundary Conditions
Composite consisting two different solid layers for which the bottom surface is assumed to be adiabatic and the interface characterized by a perfect thermal contact is considered. For 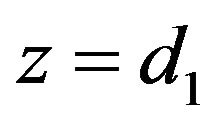 we obtained from Equation (13) the corresponding subsidiary equation
we obtained from Equation (13) the corresponding subsidiary equation
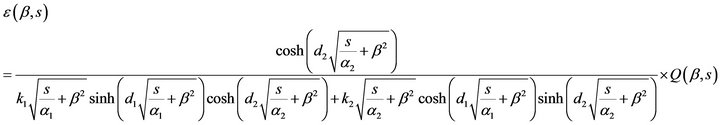
(18)
Using Equations (14) and (15) here gives Using the binomial series expansion as before we get,
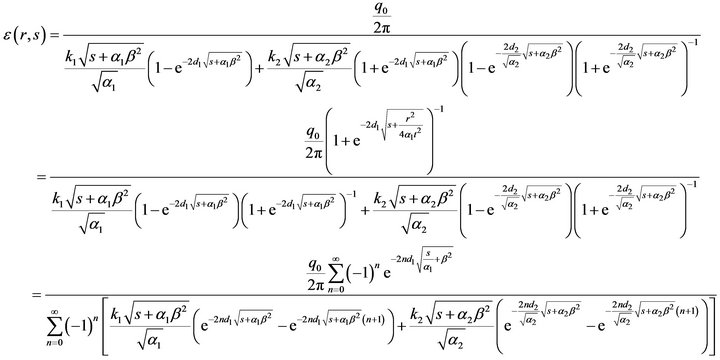
(19)
Equation (19) can now be converted to t domain using the Laplace transform conversion table [9, pp. 268-271, Rule 41 and Rule 43] with slight modifications as done previously.
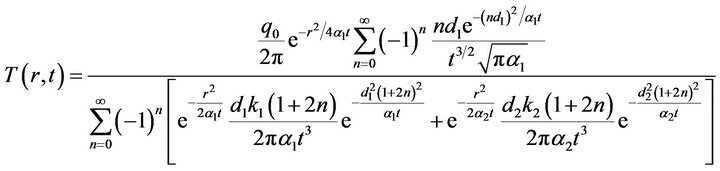
(20)
It is noted that Equation (20) is made up of three parts: the radial diffusion part represented by the first exponential term with the radial diffusion time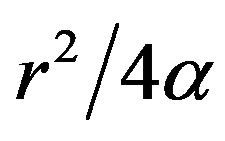 , the axial diffusion part represented by the second exponential term with diffusion time
, the axial diffusion part represented by the second exponential term with diffusion time 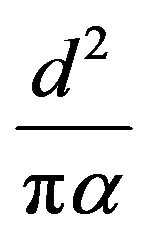 and the input energy averaged over the azimuthal angle
and the input energy averaged over the azimuthal angle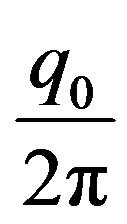 .
.
5. Simulation Results
The behaviour of Equation (20) with different values of radius of heating ring r (m), input laser energy q (J), thermal diffusivities of the film 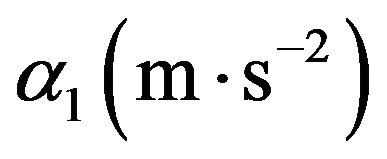 and that of the substrate
and that of the substrate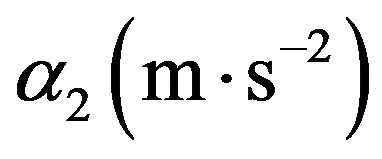 , and their thicknesses
, and their thicknesses 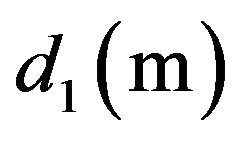 and
and 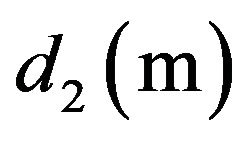 respectively were tested and simulated using MATHEMATICA (version 6) Software and the results are shown in Figures 1 to 6 respectively.
respectively were tested and simulated using MATHEMATICA (version 6) Software and the results are shown in Figures 1 to 6 respectively.
6. Conclusion
Many of the subsidiary equations related to heat diffusion problems in composite media contains hyperbolic functions of 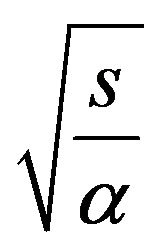 , these functions can be expanded in a series of negative exponentionals and the resulting expression inverted term by term using the Laplace
, these functions can be expanded in a series of negative exponentionals and the resulting expression inverted term by term using the Laplace

Figure 1. Simulation result for different values of radius of heating ring, r.
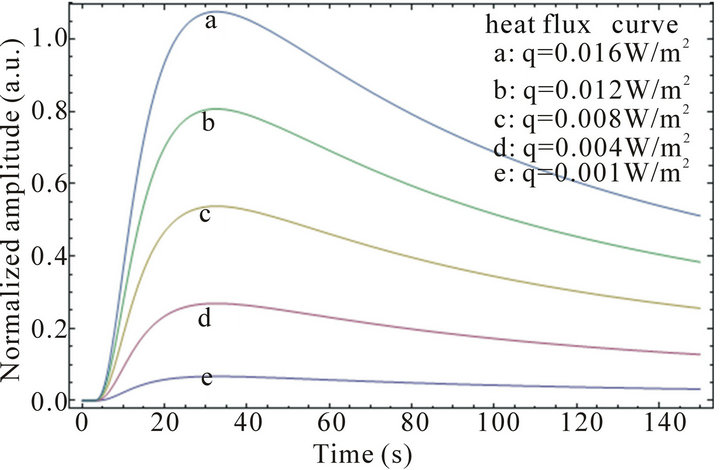
Figure 2. Simulation results for different values of laser input energy, q.
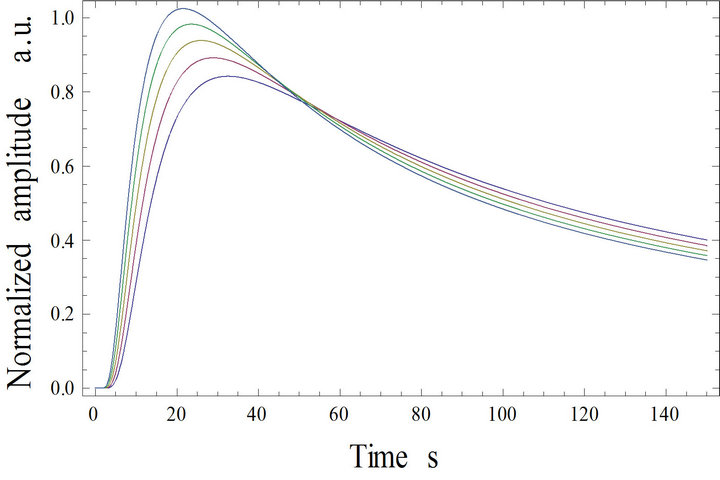
Figure 3. Simulation results for different values of thermal diffusivity a1 of film.
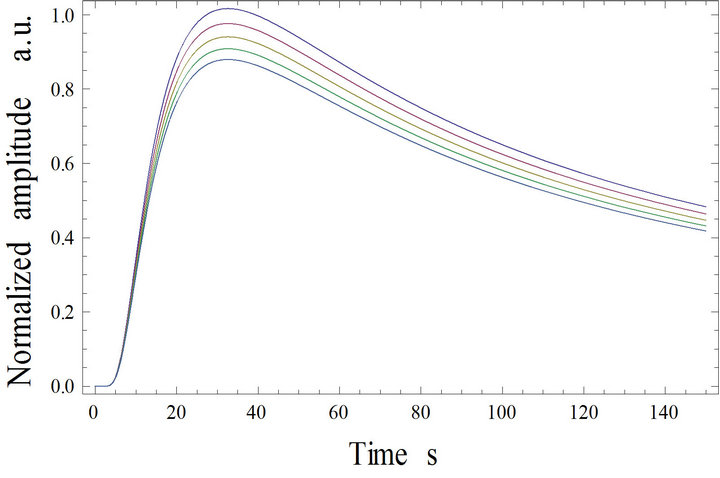
Figure 4. Simulation results for different values of thermal diffusivity a2 of substrate.
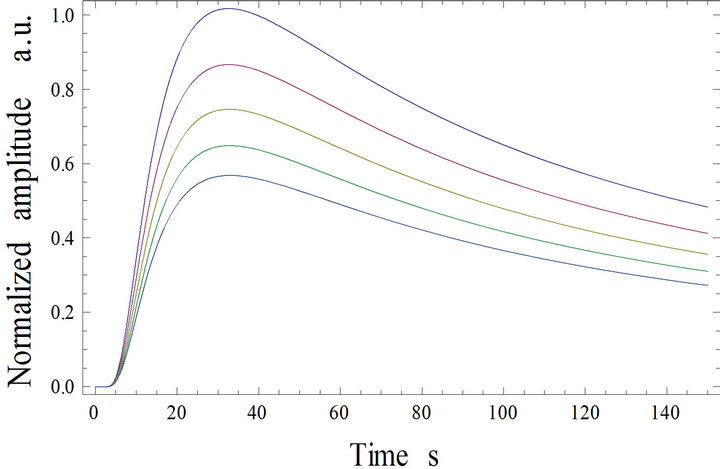
Figure 5. Simulation results for different values of thickness d1 of film.

Figure 6. simulation results for different values of thickness d2 of substrate.
transform conversion table as illustrated with two examples above. This technique is not only easy and straight forward but it is also noted that this form is often more useful than those obtained by integral inversion theorem, especially for small values of time [10].
REFERENCES
- W. J. Parker, R. J. Jenkins, C. P. Butler and G. L. Abbot, “Flash Method of Determining Thermal Diffusivity, Heat Capacity, and Thermal Conductivity,” Journal of Applied Physics, Vol. 32, No. 9, 1961, p. 1679-1684. doi:10.1063/1.1728417
- K. B. Larson and K. Koyama, “Measurement by the Flash Method of Thermal Diffusivity, Heat Capacity, and Thermal Conductivity in Two Layer Composite Sample,” Journal of Applied Physics, Vol. 39, No. 9, 1968, pp. 4408-4416.
- M. K. El-Adawi, M. A. Abdel-Naby and S. A. Shalaby, “Laser Heating of a Two-Layer System with Constant Surface Absorption: An Exact Solution,” International Journal of Heat and Mass Transfer, Vol. 38, No. 5, 1995, pp. 947-952. doi:10.1016/0017-9310(94)00162-O
- Y. Jannot, A. Degiovanni and G. Payet, “Thermal Conductivity Measurement of Insulating Materials with a Three Layers Device,” International Journal of Heat and Mass Transfer, Vol. 52, No. 5-6, 2009, pp. 1105-1111. doi:10.1016/j.ijheatmasstransfer.2008.09.017
- R. L. Mcmasters and R. B. Dinwiddie, “A Sensitivity Analysis of a Thin Film Conductivity Estimation Method,” Proceeding of the 30th International Thermal Conductivity Conference, Pittsburgh, 29 August-2 September 2009, pp. 1403-1411.
- D. L. Balageas, J. C. Krapez and P. Cielo, “Pulsed Photothermal Modelling of Layered Materials,” Journal of Applied Physics, Vol. 59, No. 2, 1986, pp. 348-357. doi:10.1063/1.336690
- S. E.-S. Abd El-Ghany, “The Temperature Profile in the Molten Layer of a Thin-Film Coated on a Substrate Induced by Irradiation with a Pulsed Laser,” Optics and Laser Technology, Vol. 36, No. 2, 2004, pp. 95-106. doi:10.1016/S0030-3992(03)00139-7
- P. Hui and H. S. Tan. “Modelling of Thermal Measurement of Diamond Thin Films Using a Pulsed Laser Technique,” Surface and Coating Technology, Vol. 62, No. 1-3, 1993, pp. 361-366. doi:10.1016/0257-8972(93)90268-S
- M. N. Ozisik. “Heat Conduction,” 2nd Edition, John Wiley and Sons Inc., New York, 1993, pp. 268-271.
- H. S. Carslaw and J. C. Jaeger, “Conduction of Heat in Solids,” 2nd Edition, Oxford University Press, London, 1959.
- N. W. McLachlan, “Complex Variable Theory and Transform Calculus,” Cambridge University Press, London, 1953.
- H. S. Carslaw and J. C. Jaeger, “Operational Methods in Applied Mathematics,” Oxford University Press, London, 1948.
- S. Goldstein, “On the Operational Determination of Two Dimensional Greens Functions in the Theory of Heat Conduction,” Proceedings of London Mathematical Society, 2nd Series, Vol. 34, 1932, pp. 51-88.
NOTES
*Corresponding author.

