Engineering
Vol. 4 No. 3 (2012) , Article ID: 18337 , 6 pages DOI:10.4236/eng.2012.43022
Reflection of Plane Waves from Free Surface of an Initially Stressed Rotating Orthotropic Dissipative Solid Half-Space
1Department of Mathematics, Post Graduate Government College, Chandigarh, India
2Baba Saheb Ambedkar Institute of Technology and Management, Faridabad, India
Email: bsinghgc11@gmail.com
Received December 2, 2011; revised December 26, 2011; accepted January 10, 2012
Keywords: Orthotropic; Dissipative Medium; Initial Stress; Rotation; Plane Waves; Reflection; Reflection Coefficients
ABSTRACT
The governing equations of an initially stressed rotating orthotropic dissipative medium are solved analytically to obtain the velocity equation which indicates the existence of two quasi-planar waves. The appropriate particular solutions in the half-space satisfy the required boundary conditions at the stress-free surface to obtain the expressions of the reflection coefficients of the reflected quasi-P (qP) and reflected quasi-SV (qSV) waves in closed form for the incidence of qP and qSV waves. A particular model is chosen for numerical computation of these reflection coefficients for a certain range of the angle of incidence. The numerical values of these reflection coefficients are shown graphically against the angle of incidence for different values of initial stress parameter and rotation parameter. The impact of initial stress and rotation parameters on the reflection coefficients is observed significantly.
1. Introduction
The Earth is considered as an elastic body with various additional parameters, e.g. porosity, initial stress, viscosity, dissipation, temperature, voids, diffusion, etc. Initial stresses in a medium are caused by various reasons such as creep, gravity, external forces, difference in temperatures, etc. The reflection of plane waves at free surface, interface and layers is important in estimating the correct arrival times of plane waves from the source. Various researchers studied the reflection and transmission problems at free surface, interfaces and in layered media [1- 12]. The study of the reflection of plane waves in the presence of initial stresses and dissipation finds significant applications in various engineering fields. Following Biot [13] theory of incremental deformation, Selim [14] studied the reflection of plane waves at a free surface of an initially stressed dissipative medium. Recently, Singh and Arora [15] studied the reflection of plane waves from a free surface of an initially stressed transversely isotropic dissipative medium.
In the present paper, we studied the problem on reflection of plane waves at a stress-free surface of an initially stressed rotating orthotropic dissipative solid half-space. The reflection coefficients of reflected waves are computed numerically to observe the effects of initial stress and rotation.
2. Formulation of the Problem and Solution
We consider an initially stressed orthotropic half-space rotating about y-axis 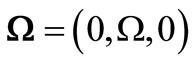 with
with . Following Biot [13] and Schoenberg and Censor [16], the basic dynamical equations of motion in x-z plane for an infinite, initially stressed and rotating medium, in the absence of external body forces are,
. Following Biot [13] and Schoenberg and Censor [16], the basic dynamical equations of motion in x-z plane for an infinite, initially stressed and rotating medium, in the absence of external body forces are,
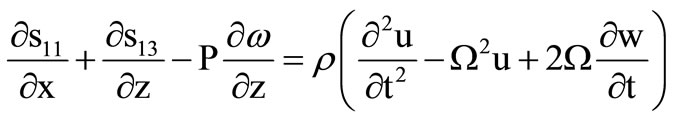 (1)
(1)
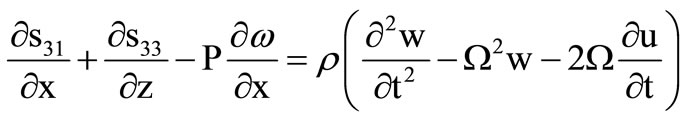 (2)
(2)
where r is the density, 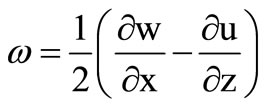 is rotational component, sij (i, j = 1, 3) are incremental stress components, u and w arethe displacement components.
is rotational component, sij (i, j = 1, 3) are incremental stress components, u and w arethe displacement components.
Following Biot [13], the stress-strain relations are:
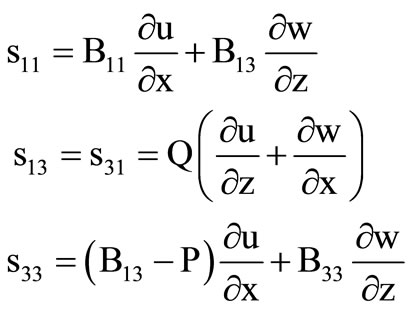 (3)
(3)
where Cij are the incremental elastic coefficients.
For dissipative medium, elastic coefficients are replaced by the complex constants:
 (4)
(4)
where, 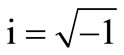 ,
,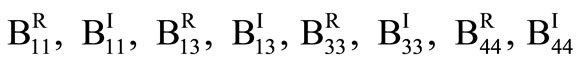 are real. Following Fung [17], the stress and strain components in dissipative medium are,
are real. Following Fung [17], the stress and strain components in dissipative medium are,
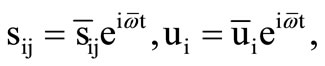 (5)
(5)
where (i, j = 1, 3) and 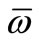 being the angular frequency.
being the angular frequency.
With the help of Equations (4) and (5), the Equation (3) becomes,
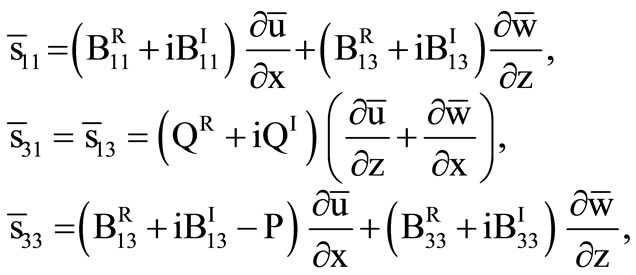 (6)
(6)
The displacement vector  is given by
is given by 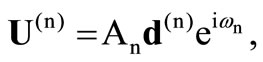 where (n) assigns an arbitrary direction of propagation of waves,
where (n) assigns an arbitrary direction of propagation of waves, 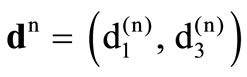
is the unit displacement vector and
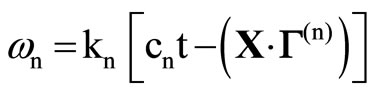
is the phase factor, in which 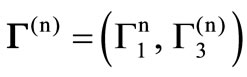 is the unit propagation vector, cn is the velocity of propagation,
is the unit propagation vector, cn is the velocity of propagation, 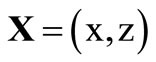 , and kn is corresponding wave number, which is related to the angular frequency by
, and kn is corresponding wave number, which is related to the angular frequency by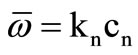 . The displacement components u(n) and w(n) are written as
. The displacement components u(n) and w(n) are written as
 (7)
(7)
Making use of Equations (6) and (7) into the Equations (1) and (2), we obtain a system of two homogeneous equations, which has non-trivial solution if
 (8)
(8)
where,
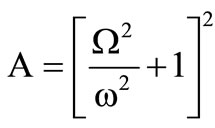 ,
, 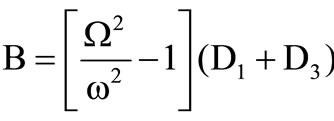 ,
, 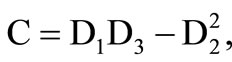
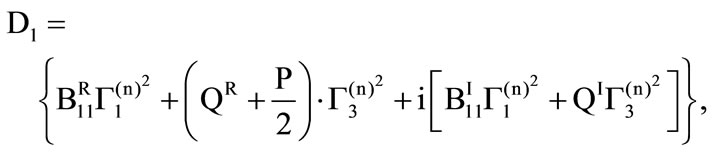
The roots correspond to quasi-P (qP) waves and quasi-SV (qSV) waves respectively. These two roots give the square of velocities of propagation as well as damping. Real parts of the right hand sides correspond to phase velocities and the respective imaginary parts correspond to damping velocities of qP and qSV waves, respectively. It is observed that both
correspond to quasi-P (qP) waves and quasi-SV (qSV) waves respectively. These two roots give the square of velocities of propagation as well as damping. Real parts of the right hand sides correspond to phase velocities and the respective imaginary parts correspond to damping velocities of qP and qSV waves, respectively. It is observed that both  and
and 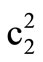 depend on initial stresses, rotation, damping and direction of propagation
depend on initial stresses, rotation, damping and direction of propagation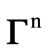 . In the absence of initial stresses, rotation and damping, the above analysis corresponds to the case of orthotropic elastic solid.
. In the absence of initial stresses, rotation and damping, the above analysis corresponds to the case of orthotropic elastic solid.
3. Reflection of Plane Waves from Free Surface
We consider an initially stressed rotating orthotropic dissipative half-space occupying the region z > 0 (Figure 1). In this section, we shall drive the closed form expressions for the reflection coefficients for incident qP or qSV waves.
The displacement components of incident and reflected waves are as,
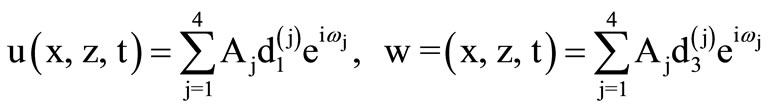 (9)
(9)
where,
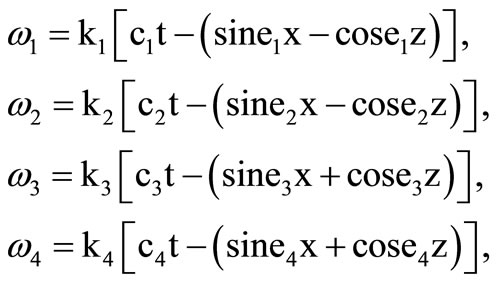 (10)
(10)
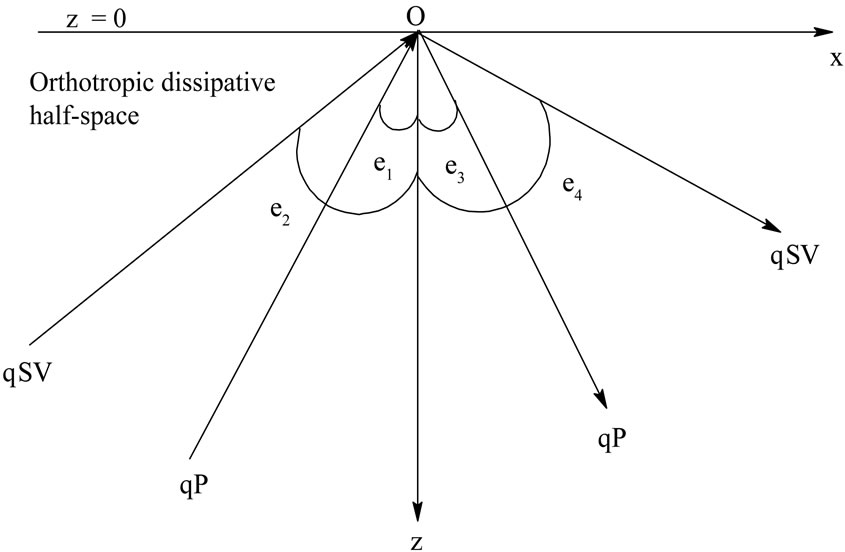
Figure 1. Geometry of the problem.
Here, subscripts 1, 2, 3 and 4 correspond to incident qP wave, incident qSV wave, reflected qP wave and reflected qSV wave, respectively.
In the x-z plane, the displacement and stress components due to the incident qP wave 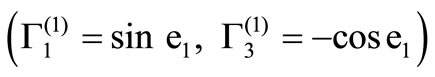 are written as
are written as
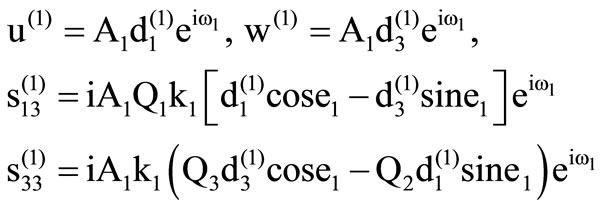 (11)
(11)
where,
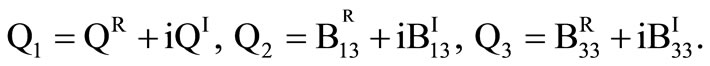
In the x-z plane, the displacement and stress components due to the incident qSV wave 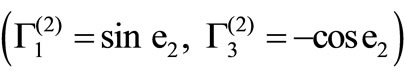 are written as
are written as
 (12)
(12)
In the x-z plane, the displacement and stress components due to the reflected qP wave 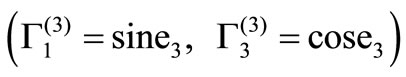 are written as
are written as
 (13)
(13)
In the x-z plane, the displacement and stress components due to the reflected qSV wave 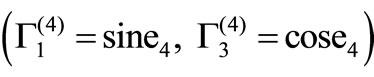 are written as
are written as
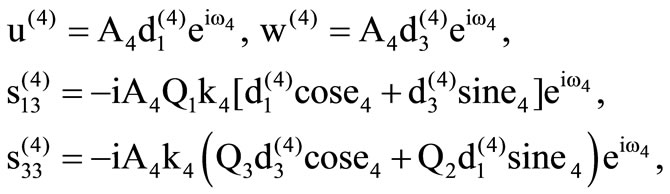 (14)
(14)
The boundary conditions required to be satisfied at the free surface z = 0,
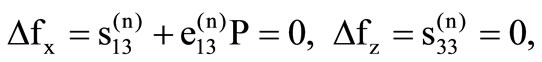 (15)
(15)
The above boundary conditions are written as
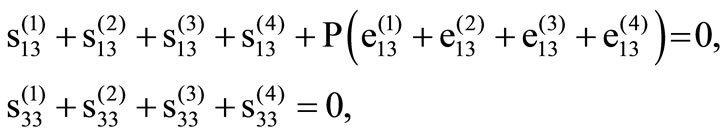 (16)
(16)
The Equations (11) to (14) will satisfy the boundary conditions (16), if the following Snell’s law holds
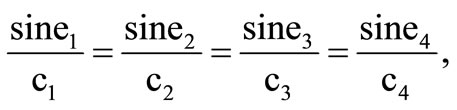 (17)
(17)
with the following relations A1δ1 + A2δ2 + A3δ3 + A4δ4 = 0, (18)
A1δ5 + A2δ6 + A3δ7 + A4δ8 = 0, (19)
where
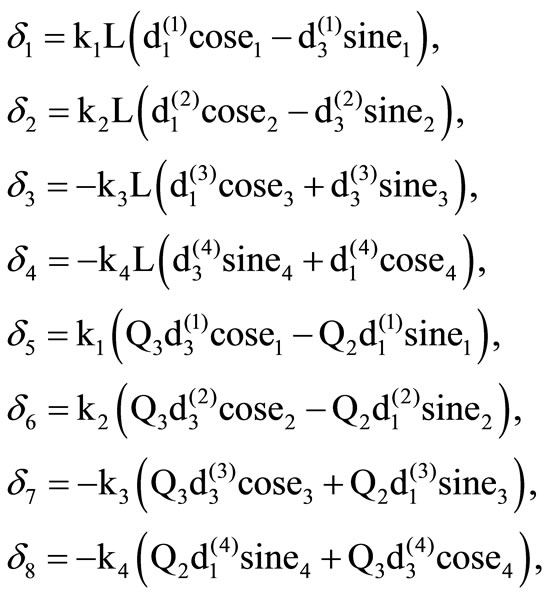 (20)
(20)
and .
.
For incident qP wave (A2 = 0), we obtain from equations (18) and (19),
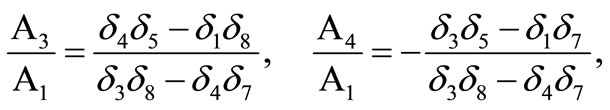 (21)
(21)
For incident qSV wave (A1 = 0), we obtain from equations (18) and (19),
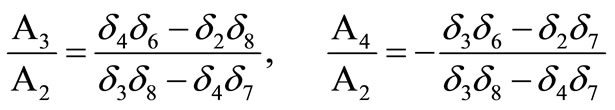 (22)
(22)
For isotropic case, B11 = λ + 2μ + P, B13 = λ + P, B33 = λ + 2μ, Q = μ, P = –S11, Ω = 0, then the above theoretical derivations reduce to those obtained by Selim [14]
4. Numerical Example
For numerical purpose, a particular example of the material (Zinc) is chosen with the following physical constants,
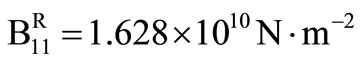 ,
, 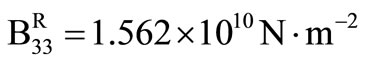 ,
,
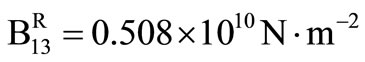 ,
, 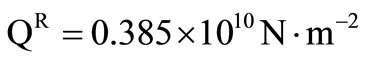 ,
,
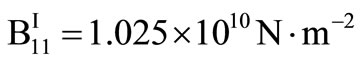 ,
, 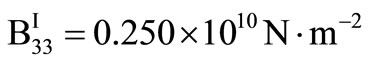 ,
,
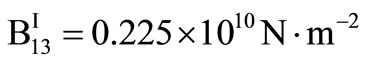 ,
, 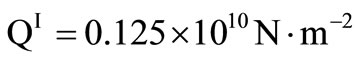 ,
,
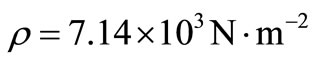 .
.
From Equations (21) and (22), the reflection coefficients of reflected qP and qSV waves are computed for the incident qP and qSV waves. The numerical values of the reflection coefficients of reflected qP and qSV waves are shown graphically in Figures 2 and 3 for incident qP wave and in Figures 4 and 5 for incident qSV wave.
In Figure 2, from comparison of solid line with dashed lines, it is observed that the reflection coefficients of qP and qSV waves change due to the presence of initial stresses at each angle of incidence of qP wave except
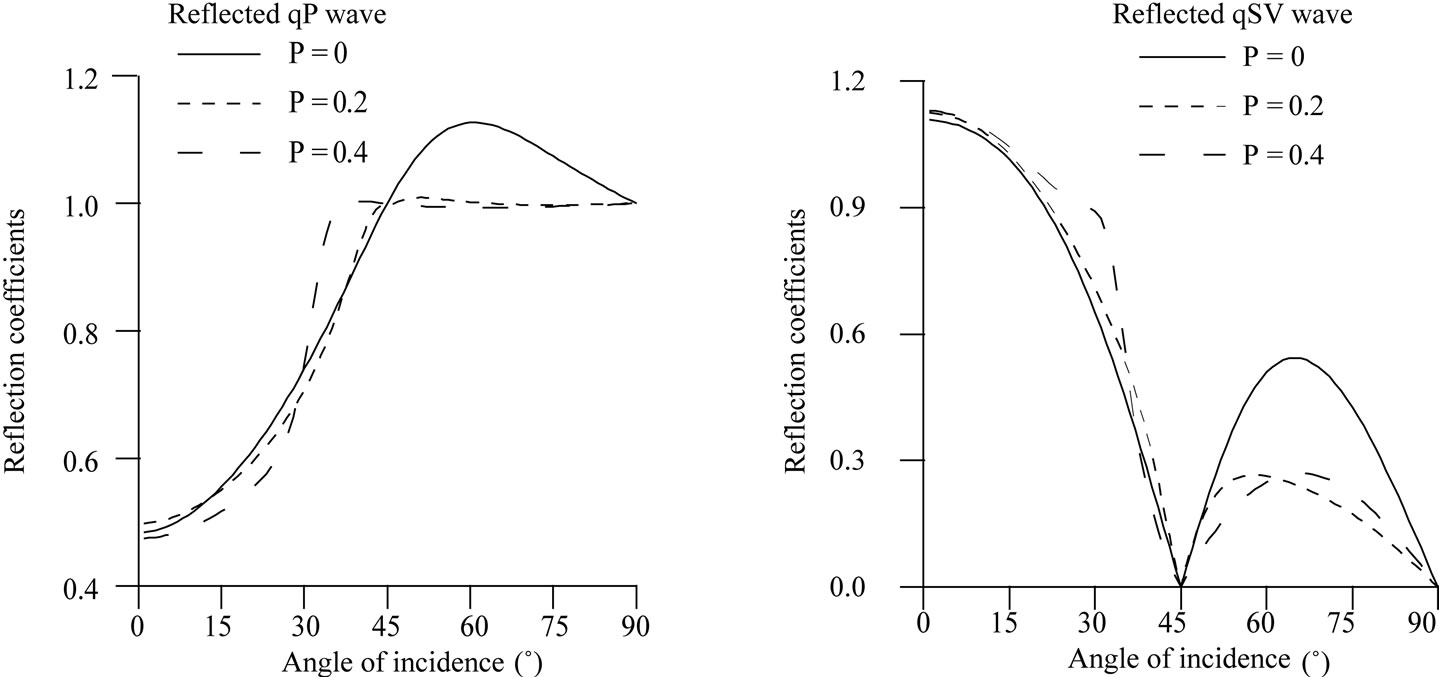
Figure 2. Effect of initial stresses on the reflection coefficients of qP and qSV waves for incidence of qP wave.
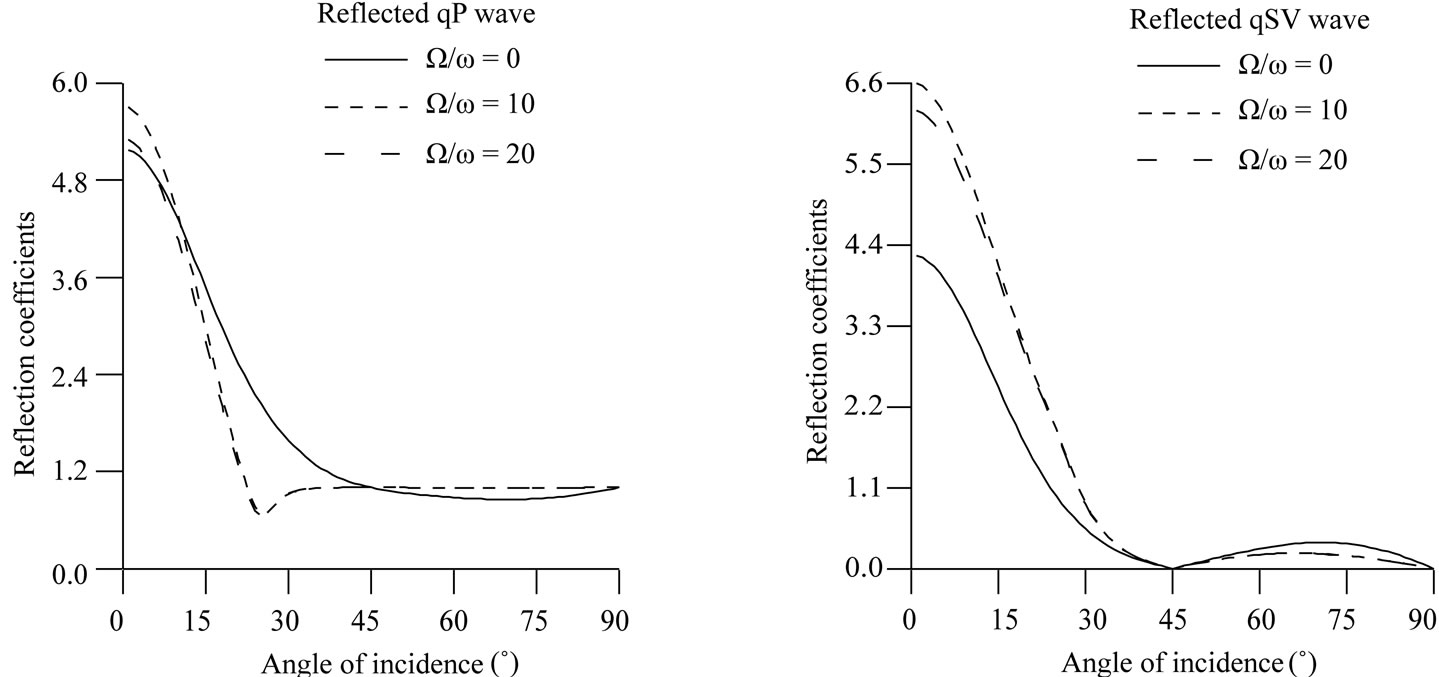
Figure 3. Effect of rotation parameter on the reflection coefficients of qP and qSV waves for incidence of qP wave.
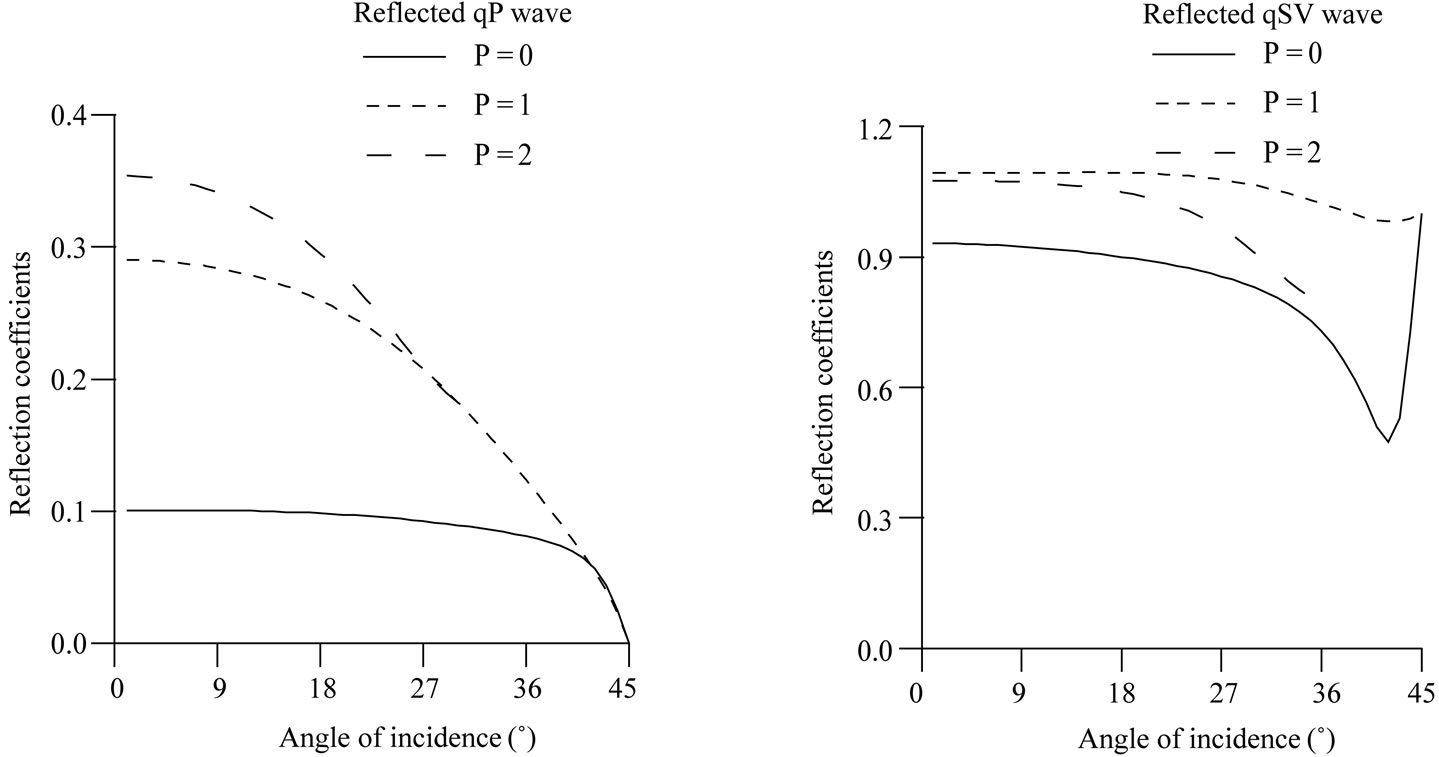
Figure 4. Effect of initial stresses on the reflection coefficients of qP and qSV waves for incidence of qSV wave.
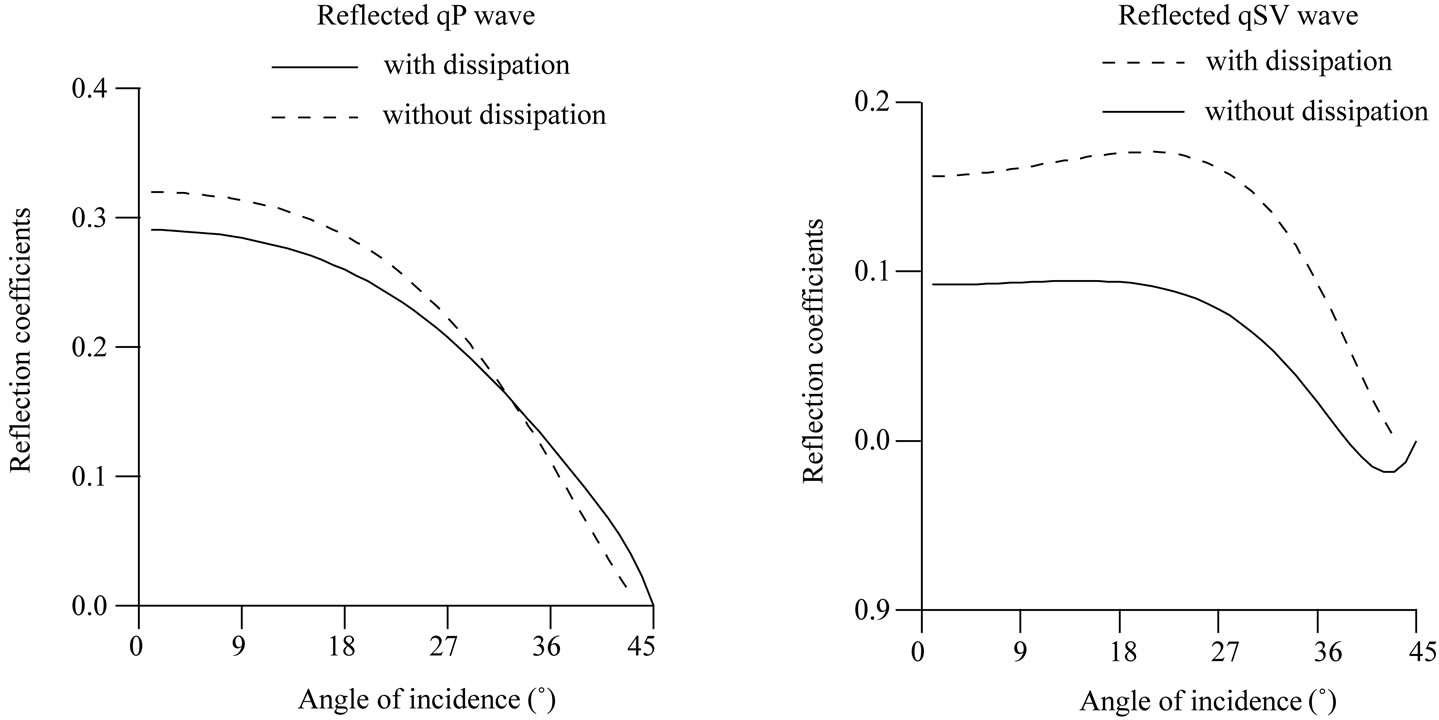
Figure 5. Effect of dissipation on the reflection coefficients of qP and qSV waves for incidence of qSV wave.
grazing incidence. The effect of initial stresses is observed maximum in the range 45˚ < e1 < 90˚.
From Figure 3, it is observed that the reflection coefficients of qP and qSV waves change due to the presence of rotation in the medium at each angle of incidence of qP wave except grazing incidence.
In Figure 4, from comparison of solid line with dashed lines, it is observed that the reflection coefficients of qP and qSV waves change due to the presence of initial stresses in the medium at each angle of incidence of qSV wave except grazing incidence.
From Figure 5, it is observed that the reflection coefficients of qP and qSV waves change due to the presence of dissipation in the medium at each angle of incidence of qSV wave.
5. Conclusions
The reflection from the stress-free surface of an initially stressed rotating orthotropic dissipative medium is considered. The expressions for the reflection coefficients of reflected qP and qSV waves are obtained in closed form for the incidence of qP and qSV waves. For a particular material, these coefficients are computed and depicted graphically against the angle of incidence for different values of initial stress and rotation parameters. From the figures, it observed that 1) the initial stresses affect significantly the reflection coefficients of reflected qP and qSV waves; 2) the rotation parameter also affects significantly the reflection coefficients of qP and qSV waves; 3) Reflection coefficients are also affected due to the presence of dissipation.
REFERENCES
- S. B. Sinha, “Transmission of Elastic Waves through a Homogenous Layer Sandwiched in Homogenous Media,” Journal of Physics of the Earth, Vol. 12, No. 1, 1999, pp. 1-4. doi:10.4294/jpe1952.12.1
- R. N. Gupta, “Reflection of Plane Waves from a Linear Transition Layer in Liquid Media,” Geophysics, Vol. 30, No. 1, 1965, pp. 122-131. doi:10.1190/1.1439528
- R. D. Tooly, T. W. Spencer and H. F. Sagoci, “Reflection and Transmission of Plane Compressional Waves,” Geophysics, Vol. 30, No. 4, 1965, pp. 552-570. doi:10.1190/1.1439622
- R. N. Gupta, “Reflection of Elastic Waves from a Linear Transition Layer,” Bulletin of the Seismological Society of America, Vol. 56, No. 2, 1966, pp. 511-526.
- R. N. Gupta, “Propagation of SH-Waves in Inhomogeneous Media,” Journal of Acoustical Society of American, Vol. 41, No. 5, 1967, pp. 1328-1329. doi:10.1121/1.1910477
- H. K. Acharya, “Reflection from the Free Surface of Inhomogeneous Media,” Bulletin of the Seismological Society of America, Vol. 60, No. 4, 1970, pp. 1101-1104.
- V. Cerveny, “Reflection and Transmission Coefficients for Transition Layers,” Studia Geophysica et Geodaetica, Vol. 18, No. 1, 1974, pp. 59-68. doi:10.1007/BF01613709
- B. M. Singh, S. J. Singh and S. D. Chopra, “Reflection and Refraction of SH-Waves and the Plane Boundary between Two Laterally and Vertically Heterogeneous Solids,” Acta Geophysica Polonica, Vol. 26, 1978, pp. 209- 216.
- B. Singh, “Effect of Hydrostatic Initial Stresses on Waves in a Thermoelastic Solid Half-Space” Applied Mathematics and Computation, Vol. 198, No. 2, 2008, pp. 498-505. doi:10.1016/j.amc.2007.08.072
- M. D. Sharma, “Effect of Initial Stress on Reflection at the Free Surfaces of Anisotropic Elastic Medium,” Journal of Earth System Science, Vol. 116, No. 6, 2007, pp. 537-551. doi:10.1016/j.amc.2007.08.072
- S. Dey and D. Dutta, “Propagation and Attenuation of Seismic Body Waves in Initially Stressed Dissipative Medium,” Acta Geophysica Polonica, Vol. 46, No. 3, 1998, pp. 351-365.
- M. M. Selim and M. K. Ahmed, “Propagation and Attenuation of Seismic Body Waves in Dissipative Medium Under Initial and Couple Stresses,” Applied Mathematics and Computation, Vol. 182, No. 2, 2006, pp 1064-1074. doi:10.1016/j.amc.2007.08.072
- M. A. Biot, “Mechanics of Incremental Deformation,” John Wiley and Sons Inc., New York, 1965.
- M. M. Selim, “Reflection of Plane Waves at Free Surface of an Initially Stressed Dissipative Medium,” World Academy Science, Engineering & Technology, Vol. 40, 2008, pp. 36-43.
- B. Singh and J. Arora, “Reflection of Plane Waves from a Free Surface of an initially Stressed Transversely Isotropic Dissipative Medium,” Applied Mathematics, Vol. 2, No. 9, 2011, pp. 1129-1133. doi:10.4236/am.2011.29156
- M. Schoenberg and D. Censor, “Elastic Waves in Rotating Media,” Quarterly of Applied Mathematics, Vol. 31, 1973, pp. 115-125.
- Y. C. Fung, “Foundation of Solid Mechanics,” Prentice Hall of India, New Delhi, 1965.

