Engineering
Vol. 4 No. 1 (2012) , Article ID: 17098 , 7 pages DOI:10.4236/eng.2012.41006
Maintenance Capacity Planning: Determination of Maintenance Workforce
Industrial Engineering Department, College of Engineering, King Saud University, Riyadh, Kingdom of Saudi Arabia
Email: alshayea@ksu.edu
Received October 5, 2011; revised November 12, 2011; accepted November 22, 2011
Keywords: Maintenance Workforce Size; Maintenance Workload; Maintenance Backlog; Maintenance Resources Planning; Maintenance Programs
ABSTRACT
Determining the size of maintenance workforce is an essential element of maintenance planning. It is important for performing maintenance programs perfectly. However, it is a complex and challenging problem since it involves the consideration of several important factors. The mathematical model developed in this paper aims at finding out the optimal size of the maintenance workforce taking into account all of the important factors that affect this size. It is based on determining the needed number of workers with different skill levels and from different sources to meet maintenance workload of different grades that is to be performed in a specified planning horizon with minimum cost acquired.
1. Introduction
Maintenance function is known to be subordinate to production function. All of its objectives are concentrated toward keeping production systems in their best possible operating condition. Maintenance as a function is very important for any type of manufacturing industries. It keeps the continuation of manufacturing cycle and it is vital for supporting the overall production strategy while making the most economical use of total resources [1-4].
Manufacturing industries usually search for proper ways to apply maintenance function in their plants in order to achieve the purpose of using this function. In other words, they are in search of proper ways for planning, scheduling and executing maintenance programs to achieve organizational objectives such as availability, quality rates, reliability and delivery dates. Proper ways of executing maintenance programs depend on good scheduling of the maintenance workload which in turns depends on good planning of maintenance resources [2- 8]. Good planning means proper determination of the maintenance resources that are needed to meet the maintenance workload to be performed during the planning horizon. In particular, good planning deals with good determination of [2-8]:
• Skills of maintenance workers;
• Exact number of maintenance workers of various crafts;
• Types of maintenance equipment and tools;
• Exact number of maintenance equipment and tools;
• Specifications of spare parts and materials;
• Exact number of spare parts and materials;
• Right level of work backlog;
• Overtime capacity;
• Contract maintenance capacity.
The most complex element among all of these essential elements of planning is the determination of the exact number of maintenance workers of various crafts [2,6,9- 12]. This is because it involves meeting maintenance workload with different grade of complexity by the use of workers of different skills and from different work sources (direct hire, overtime, and contracting). This complexity stimulates researchers to find ways to determine the exact number of maintenance workers with minimum cost acquired. The efforts by the researchers to find ways to determine the maintenance workforce with minimum cost acquired when the forecasted maintenance workload, standard times, and other random variables are constants are classified into two categories. The first category represents the heuristic tableau method [2]. This method drives plans to determine a feasible number of maintenance workers based on sound principles and guidelines. The used principles and guidelines include important issues such as providing sufficient in-house workers for high priority work, a reasonable ratio between overtime work and regular-time work, and fixed healthy backlog of maintenance work. The method is based on evaluating the cost of each alternative plan and the plan with minimum cost is selected.
The second category represents the mathematical models that are developed to deal with the capacity planning of maintenance workers. The objective of these models is to determine the number of maintenance workers of different skill levels from a maintenance trade made available from different sources to perform different grades of maintenance work [2,6,8-10,13]. Each model consists of an objective function and set of constraints. The objective function is to minimize manpower cost and backlog of maintenance work cost and the constraints include the work balance constraints, a reasonable ratio between inhouse man-hours and overtime man-hours constraints, limits on labor availability constraints, and lower and upper limits on backlog of different work grade constraints. The differences between the models in this category are solving this complexity as a linear programming instead of an integer programming problem and changing the decision variables to represent number of man-hours needed instead of number of workers needed [2,6,8-10, 13].
All of the methods in these two categories succeeded in finding the number of workers with a certain skill level and from certain work source that is needed to perform maintenance workload of certain grade in each period of time of the planning horizon (period wise determination). However, they failed to solve all aspects of the complexity of determining the exact number of maintenance workers which represent a problem to the maintenance departments in the field. In particular, they failed to find the needed number of direct-hired workers for the whole planning horizon, the number of workers needed to work overtime in each period and the number of subcontracted workers in each period (planning horizon wise determination). This means that there are important issues that need to be covered as shown in Table 1. These are the following:
• Considering the needed number of workers to hire for the whole planning horizon, the number of workers needed to work overtime in each period and the number of subcontracted workers needed in each period as decisions variables.
• There should be no limits on workers availability from any source and from any skill level because setting limits means that the needed number of workers to hire for the whole planning horizon is known and presented by the limits.
• The cost of contracted workers is changing from time period to the other according to the demand of these workers and this should be reflected in the models whereas the cost parameter for the direct hired workers working in the regular day time (normal day shift) or in the overtime is fixed constant according to their contracts.
• The number of hours worked by a direct hired worker in each time period is changing from time period to the other according to the holidays in each time period and this should be reflected in the models.
The work in this paper considers these important issues. It proposes mathematical model that determines the exact number of maintenance workers of different skill levels and from different work sources needed to perform the forecasted maintenance workload and healthy work backlog with minimum cost acquired taking into consideration all of the important issues affecting the determination process including the above important issues.
2. Determining Maintenance Workforce
The optimal allocation of the maintenance workforce to meet random and varying workload is a complex and challenging problem [2,6,8-10,12]. It is a problem of determining the needed number of workers with different skill levels and from different sources to meet maintenance workload of different grades [2,6,9,10]. In particular, it is the determination of the number of direct hired, overtime, and subcontracted workers with different skill levels needed for a specified planning horizon in which maintenance workload of different grades is required to be performed with minimum cost acquired.
The determination of maintenance workforce involves the consideration of several important factors. Specifically, it involves the consideration of the following:
1) Planning horizon;
2) Maintenance workload for each maintenance work grade in each time period of the planning horizon;
3) Healthy backlog for maintenance works of each maintenance work grade in each time period of the planning horizon;
4) Productivity of maintenance workers;

Table 1. Elements of differences between previous models and the proposed model.
5) Cost of maintenance workers;
6) Cost of backlogging maintenance work.
The consideration of the planning horizon involves specifying the time length of this horizon. Also, it involves dividing the horizon into smaller time periods. In each time period of the planning horizon, the maintenance workload and the backlog of the maintenance works for each work grade are considered. The consideration of the maintenance workload for each work grade in each time period is based on forecasting these workloads whereas the consideration of the backlog of the maintenance works for each work grade in each time period is based on its cost and the healthy lower and upper limits of this backlog that are to be specified. Healthy lower and upper limits of backlogging maintenance works are those limits that will not let maintenance workers to be lazy because there are no or few backlog maintenance works or to be overreacting and overwhelming because there are a lot of backlog maintenance works to be performed.
The consideration of the productivity of the workers depends on the worker professionalism of carrying out the work and on his experience. It is different from source to source and from skill level to skill level. Basically, it is considered by dividing the time required to perform the maintenance work over the actual time spent by the worker to perform the maintenance wok.
In addition to these factors, the last two factors that need to be considered are the cost of the maintenance workers and the cost of backlogging maintenance work. The consideration of the cost of backlogging maintenance work is based on specifying the maintenance cost and the losses in production or service that are caused by backlogging maintenance work whereas the consideration of the cost of the maintenance workers is based on specifying the agreed amount of money to be paid to the worker for each time period he spent working on the maintenance work. For the direct hired and overtime workers, the cost of the worker is usually fixed constant in each time period according to signed contracts by maintenance workers and the employer. This is not the case for the subcontracted workers who are brought to the work when needed. The cost in this case is varied from time period to time period according to the demand variation on these workers.
3. Model Formulations
The model formulation is arranged in a way that describes all of the necessary aspects to determine the number of maintenance workers of different skill levels and from different work sources needed to meet the forecasted maintenance workload and the healthy work backlog that are required to be performed in a specific planning horizon. In particular, the model formulation is arranged to determine the following with minimum cost acquired:
1) The number of direct-hired workers with different skill levels who work in regular day time (normal day shift) and who are needed to perform the forecasted maintenance workload and the backlogged of the maintenance workload of different grades for the whole planning horizon.
2) The number of direct-hired workers with different skill levels needed to work overtime in order to perform the forecasted maintenance workload and the backlogged of the maintenance workload of different grades in each period of the planning horizon.
3) The number of subcontracted workers with different skill levels who work in regular day time (normal day shift) and who are needed to perform the forecasted maintenance workload and the backlogged of the maintenance workload of different grades in each period of the planning horizon.
4) The number of subcontracted workers with different skill levels needed to work overtime in order to perform the forecasted maintenance workload and the backlogged of the maintenance workload of different grades in each period of the planning horizon.
The indices, parameters, variables and equations used in the model are the following:
3.1. Indices
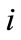 : Source of workers
: Source of workers
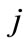 : Skill level
: Skill level
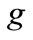 : Work grade
: Work grade
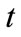 : Time period
: Time period
3.2. Parameters
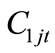 : Cost of direct hired worker of skill level
: Cost of direct hired worker of skill level 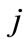 works during regular day time in period
works during regular day time in period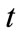 ;
;
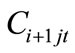 : Cost of a worker of skill level
: Cost of a worker of skill level 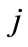 from source
from source 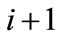 (sources of workers other than regular day time - direct hired workers) in time period
(sources of workers other than regular day time - direct hired workers) in time period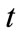 ;
;
 : Cost of backlogging one man-hour of grade
: Cost of backlogging one man-hour of grade 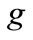 maintenance work in period
maintenance work in period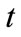 ;
;
 : Productivity of a worker of skill level
: Productivity of a worker of skill level  from source
from source 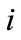 when performing a maintenance work of grade
when performing a maintenance work of grade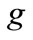 ;
;
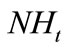 : Number of hours worked by a regular day time—direct hired worker in period
: Number of hours worked by a regular day time—direct hired worker in period ;
;
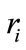 : Constant number equal to 1 if a worker is direct hired or subcontracted worker who works during regular day time, and between 0 and 1 if a worker is overtime direct hired or overtime subcontracted worker;
: Constant number equal to 1 if a worker is direct hired or subcontracted worker who works during regular day time, and between 0 and 1 if a worker is overtime direct hired or overtime subcontracted worker;
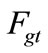 : Forecasted maintenance workload of grade
: Forecasted maintenance workload of grade 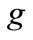 in time period
in time period ;
;
 : Upper limit of a healthy backlog for maintenance work of grade
: Upper limit of a healthy backlog for maintenance work of grade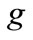 ;
;
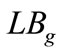 : Lower limit of a healthy backlog for maintenance work of grade
: Lower limit of a healthy backlog for maintenance work of grade .
.
3.3. Variables
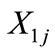 : Number of direct hired workers of skill level
: Number of direct hired workers of skill level 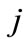 work during regular day time;
work during regular day time;
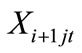 : Number of workers of skill level
: Number of workers of skill level  from source
from source 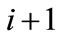 (sources of workers other than regular day time—direct hired workers) needed to work in time period
(sources of workers other than regular day time—direct hired workers) needed to work in time period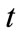 ;
;
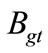 : Backlog of maintenance work of grade
: Backlog of maintenance work of grade 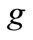 in period
in period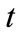 .
.
3.4. Model Constraints
The first set of constraints deals with assuring that the maintenance workload in each time period of the planning horizon is performed. In particular, it deals with balancing the sum of the number of man-hours provided by all workers of all skills and from all sources who will perform maintenance work of grade  in time period
in time period  and the backlog of maintenance work of grade
and the backlog of maintenance work of grade 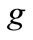 in time period
in time period 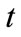 with the sum of the forecasted maintenance workload of grade
with the sum of the forecasted maintenance workload of grade  in time period
in time period 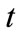 and the backlog of maintenance work of grade
and the backlog of maintenance work of grade 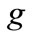 in time period
in time period .
.
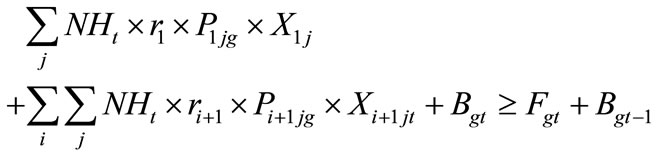 (1)
(1)
where:
The constant number  is equal to 1 because it is associated with the regular day time-direct hired workers.
is equal to 1 because it is associated with the regular day time-direct hired workers.
The second set of constraints is to make sure that the number of overtime-direct hired workers in each time period 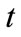 is less than or equal to regular day time-direct hired workers.
is less than or equal to regular day time-direct hired workers.
 (2)
(2)
where:
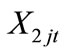 represents the number of overtime-direct hired workers in each time period
represents the number of overtime-direct hired workers in each time period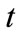 .
.
The Third set of constraints is to make sure that the number of overtime-subcontracted workers in each time period 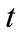 is less than or equal to regular day time-subcontracted workers.
is less than or equal to regular day time-subcontracted workers.
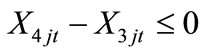 (3)
(3)
where:
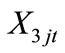 represents the number of regular day time-subcontracted workers in each time period
represents the number of regular day time-subcontracted workers in each time period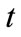 .
.
 represents the number of overtime-subcontracted workers in each time period
represents the number of overtime-subcontracted workers in each time period .
.
The last set of constraints is to make sure that the backlog of maintenance work of grade 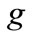 in time period
in time period  is within the lower and the upper limits of the healthy backlog for maintenance work of grade
is within the lower and the upper limits of the healthy backlog for maintenance work of grade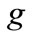 .
.
 (4)
(4)
In practical, the upper limit of the healthy backlog should not exceed the total number of maintenance hours given by the regular day time-direct hired workers. This means that the healthy backlog constraint should be revised to the following:
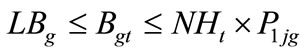 (4’)
(4’)
3.5. Model Objective Function
The model objective function has been influenced by the aim of the model which is to find the number of maintenance workers of different skill levels and from different work sources needed to meet the forecasted maintenance workload and healthy work backlog that are required to be performed in a specific planning horizon. It deals with minimizing the maintenance workers cost as well as the backlog of maintenance work cost while finding the number of maintenance workers needed to meet the forecasted maintenance workload and healthy work backlog that are required to be performed in a specific planning horizon.
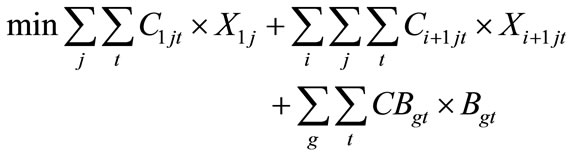 (5)
(5)
4. Case Study
Every year, maintenance department in a plant at Riyadh second industrial city works on determining its need of the electricians for performing the forecasted maintenance workload in each month of the year (the forecasted maintenance workload to be performed in each month of the next year in this plant is given in Table 2). The department classifies the maintenance work to be done by the electricians to three grades according to their level of complexities. The first grade represents maintenance works that are related to inspections, predictive maintenance and improvement maintenance whereas the second grade represents other planned and breakdown maintenance works and the third grade represents routine and running maintenance works respectively.
The backlog of maintenance works from month to month is kept within the lower and upper limits. These limits of the backlogged maintenance works have been specified by the department. They are different from

Table 2. The forecasted maintenance workload to be performed in each month of the next year.
maintenance work grade to the other as shown in Table 3. The maintenance department prefers to set the upper limit of the healthy backlog in such a way it should not exceed the total number of maintenance hours given by the regular day time-direct hired workers. In addition, it prefers to backlog an amount of maintenance works from the last month of a year to the first month of the next that is less than the upper limits (the amount of maintenance works to be backlogged to the first month of the next year is given in Table 3). The cost of backlogging maintenance works is different from maintenance grade to another while it may differ from month to month as well according to the losses in production that are caused by backlogging maintenance work. The costs of backlogging maintenance works of grade (1), grade (2) and grade (3) in each month of the planning horizon in this plant are SR 1020, SR 790 and SR 450 respectively.
The department classifies its electricians into three different types according to their skills. The first type of electricians represents those who have more than five years of experience and have passed at least four training courses. The second type represents those whose experience of performing the work is less than or equal to five years and have passed at least two training courses whereas the third type represents the newly qualified workers. The cost of each type is different according to the source to which the electrician is related (direct-hired regular day time, direct-hired overtime, subcontracted,

Table 3. The amount of maintenance works to be backlogged.
overtime subcontracted). In addition, it is different from month to month except for the direct-hired regular day time and direct-hired overtime electricians as shown in Table 4. The productivities of performing different grades of maintenance works by the department’s electricians and the subcontracted electricians are given in Table 5. The figures in the table represent the averages of the productivities of the electricians of different skill levels and from different sources.
The number of regular time hours in each month that can be provided by the electricians of different skills and from different source is given in Table 2. This number is different from month to month because of the holidays and other occasional days. In addition, it is four times as equal to the number of overtime hours that are provided by the electricians of different skills and from different source (this means that  and
and 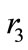 equal 1 whereas
equal 1 whereas 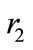 and
and 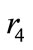 equal 0.25).
equal 0.25).
The optimum numbers of electricians of different skill levels and from different work sources needed for performing the forecasted maintenance workload in each month of the next year for this plant are found by the use of the formulated model and the results are the following:
1) Three (3) direct-hired workers of skill level (2) are needed to work in regular day time (normal day shift) for the whole planning horizon (12 months).
2) One (1) of the above mentioned direct-hired workers (direct-hired workers of skill level (2)) is needed to work overtime in the first, fifth, eighth and ninth months of the planning horizon.
3) One (1) of subcontracted workers of skill level (1) is needed to work in regular day time (normal day shift) in the second and third months of the planning horizon.
4) One (1) of subcontracted workers of skill level (2) is needed to work in regular day time (normal day shift) in the fourth, sixth, seventh and eleventh months of the
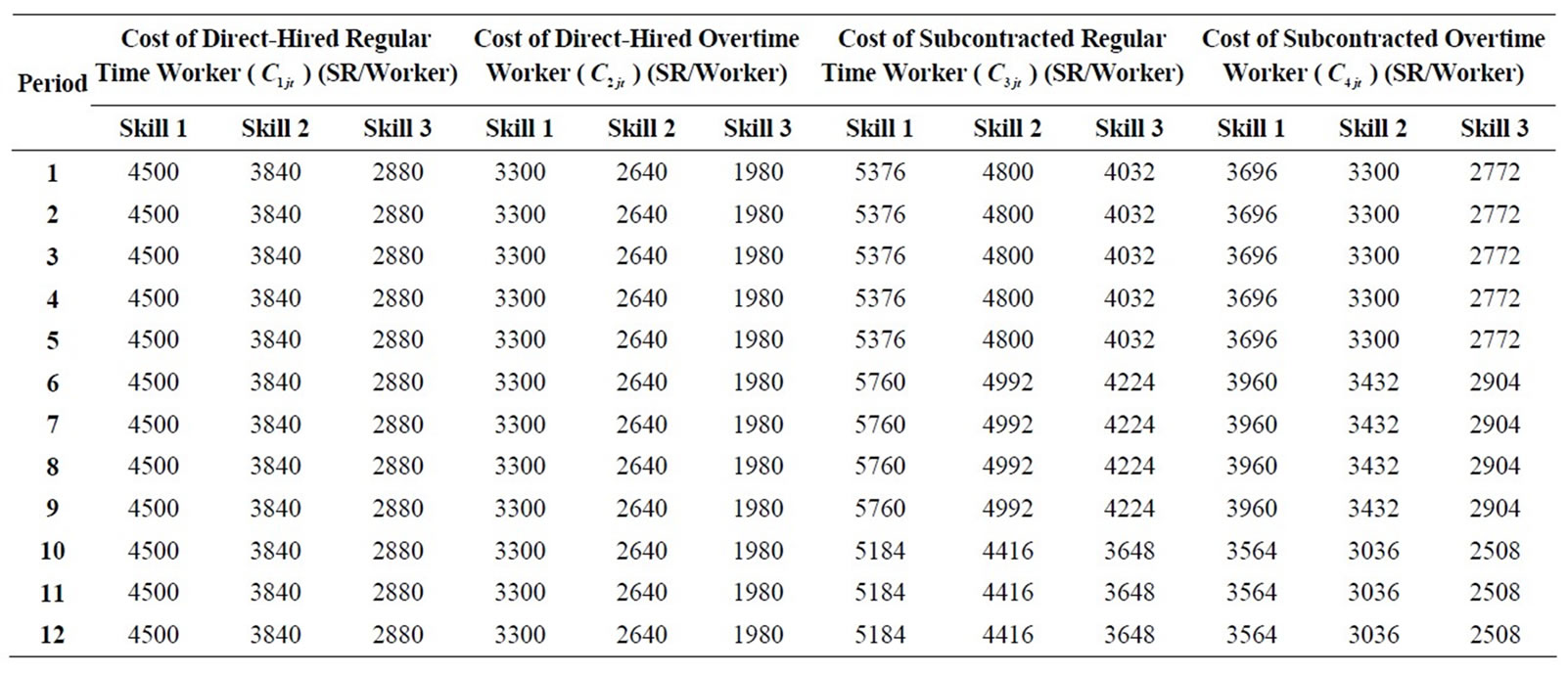
Table 4. Cost of maintenance workers.
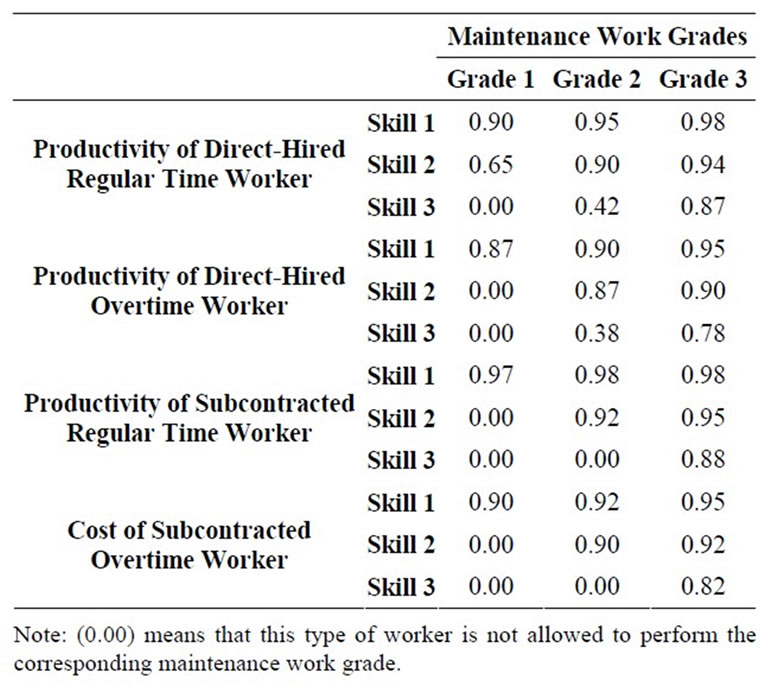
Table 5. Maintenance workers productivity.
planning horizon.
There is no backlog maintenance work. The total cost of using these numbers of electricians is SR 178752.
5. Sensitivity Analysis
In the case above, the cost of backlogging maintenance works is different from maintenance grade to another and it is fixed from month to month. However, this cost, as it has been mentioned in Section 4, may differ from month to month according to the losses in production that are caused by backlogging maintenance work. Therefore, if the cost of backlogging maintenance works is different from maintenance grade to another and from month to month as it is shown in Table 6, then the model will pick this change in the data and will give the following results:
1) Three (3) direct-hired workers of skill level (2) are needed to work in regular day time (normal day shift) for the whole planning horizon (12 months).
2) One (1) of the above mentioned direct-hired workers (direct-hired workers of skill level (2)) is needed to work overtime in the first and eighth months of the planning horizon.
3) One (1) of subcontracted workers of skill level (1) is needed to work in regular day time (normal day shift) in the second and third months of the planning horizon.
4) One (1) of subcontracted workers of skill level (2) is needed to work in regular day time (normal day shift) in the fourth, sixth, seventh and eleventh months of the planning horizon.
There is no backlog maintenance work except in the fifth and ninth months in which the backlog was 20 and 6 hours of the maintenance work of grade (2) respectively. The total cost of using these numbers of electricians and the backlog of the maintenance work is SR 176372. These results are congruent with the change that has been made.
6. Conclusions
Good planning of maintenance workforce helps industrial plants to perform their maintenance programs in an efficient and effective way. This, in turns, keeps the reliability and the availability of the production systems in these plants at their higher levels. Reaching higher levels of reliability and availability assists the industrial plants to achieve other organizational objectives such as meeting the desired quality rates and delivery dates.
Developing model to determine optimum size of the maintenance workforce is important issue. It is complex
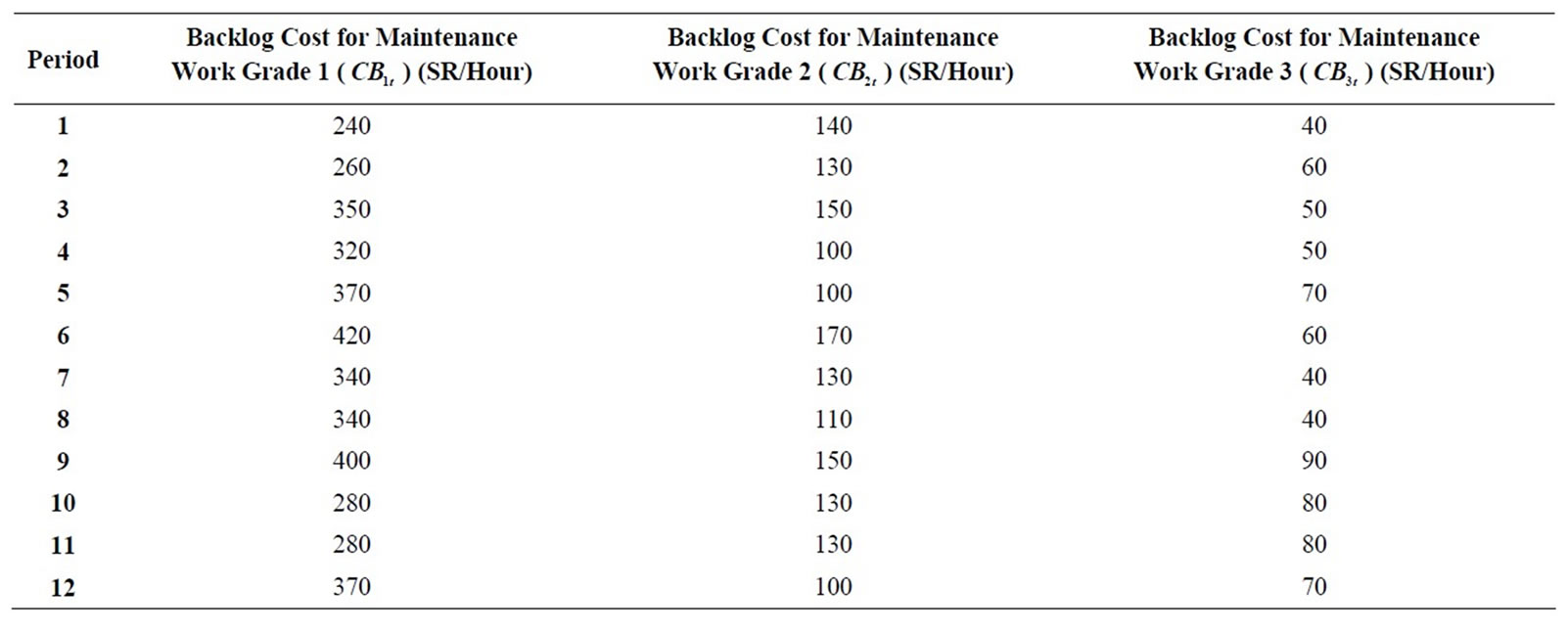
Table 6. The revised cost of backlogging maintenance works.
and challenging problem. However, when the factors that affect the determination process are considered, the developing process of the model becomes manageable.
REFERENCES
- I. Alsyouf, “The Role of Maintenance in Improving Companies’ Productivity and Profitability,” International Journal of Production Economics, Vol. 105, No. 1, 2007, pp. 70-80. doi:10.1016/j.ijpe.2004.06.057
- S. Duffuaa, A. Raouf and J. Campbell, “Planning and Control of Maintenance Systems: Modeling and Analysis,” John Wiley & Sons, New York, 1999.
- A. Kelly, “Plant Maintenance Management Set,” Butterworth Heinemann, Oxford, 2006.
- R. Smith and B. Hawkins, “Lean Maintenance,” Butterworth Heinemann, Oxford, 2004.
- I. Alsyouf, “Maintenance Practices in Swedish Industries: Survey Results,” International Journal of Production Economics, Vol. 121, No. 1, 2009, pp. 212-223. doi:10.1016/j.ijpe.2009.05.005
- A. Ashayeri, A. Teelen and W. Selen, “A Production and Maintenance Planning Model for the Process Industry,” International Journal of Production Research, Vol. 34, No. 12, 1996, pp. 3311-3326. doi:10.1080/00207549608905092
- A. Banerjee and J. Burton, “Equipment Utilization Based Maintenance Task Scheduling in a Job Shop,” European Journal of Operational Research, Vol. 45, No. 2-3, 1990, pp. 191-202. doi:10.1016/0377-2217(90)90184-D
- S. Kamran and J. Moghaddam, “Preventive Maintenance and Replacement Scheduling for Repairable and Maintainable Systems Using Dynamic Programming,” Computers and Industrial Engineering, Vol. 60, No. 4, 2011, pp. 654-665. doi:10.1016/j.cie.2010.12.021
- J. Aston and A. Gillson, “Optimization of the Maintenance Force in a Company Producing Drop Forgings,” Journal of Mechanical Working Technology, Vol. 4, No. 1, 1980, pp. 31-49. doi:10.1016/0378-3804(80)90004-2
- M. Lilly, I. Emovon, S. Ogaji and S. Probert, “Four-Day Service-Staff Work-Week in Order to Complete Maintenance Operations More Effectively in a Nigerian PowerGenerating Station,” Applied Energy, Vol. 84, No. 10, 2007, pp. 1044-1055. doi:10.1016/j.apenergy.2007.02.012
- L. Swanson, “An Empirical Study of the Relationship between Production Technology and Maintenance Management,” International Journal of Production Economics, Vol. 53, No. 2, 1997, pp. 191-207. doi:10.1016/S0925-5273(97)00113-8
- L. Swanson, “An Information-Processing Model of Maintenance Management,” International Journal of Production Economics, Vol. 83, No. 1, 2003, pp. 45-64. doi:10.1016/S0925-5273(02)00266-9
- R. Dekker and P. Scarf, “On the Impact of Optimization Models in Maintenance Decision Making: The State of the Art,” Reliability Engineering & Systems Safety, Vol. 60, No. 2, 1998, pp. 111-119. doi:10.1016/S0951-8320(98)83004-4

