Engineering
Vol. 3 No. 9 (2011) , Article ID: 7330 , 6 pages DOI:10.4236/eng.2011.39111
Study of Tsunamis by Dimensional Analysis
Department of Chemical Engineering, Amirkabir University of Technology, Tehran, Iran
E-mail: ghasemi.samira@gmail.com
Received December 18, 2010; revised June 10, 2011; accepted June 25, 2011
Keywords: Dimensional Analysis, Wavelength, Period, Dimensionless Number
ABSTRACT
Tsunamis are among the most terrifying natural hazards known to man and have been responsible for tremendous loss of life and property throughout history. In this paper by means of dimensional analysis, important non-dimensional groups in Tsunamis was studied and an equation to calculate the power of tsunamis was obtained. Also by this method and using tsunami basic physics, the height of waves near the coastline was estimated and results were compared by reported values.
1. Introduction
In recent years, there have been a number of zone earthquakes that have generated unexpectedly large local tsunamis. On Sunday, 26 December 2004, the greatest earthquake in 40 years occurred about 150 kilometers off the west coast of northern Sumatra Island in Indonesia. [1-6]. The tsunami death toll is estimated at 300,000. The quake was widely felt in Sumatra, the Nicobar and Andaman Islands, Malaysia, Myanmar, Singapore, Thailand, Bangladesh and India [7,8].
According to the U. S. Geological Survey (USGS NEIC (WDCS-D)), the moment magnitude of the earthquake—which is larger than the Richter magnitude—was 9. Such magnitude would make this earthquake to be the fourth largest in the world since 1900 [1]. But others [7-11] reported the magnitude of this earthquake to be 9.3 Richter.
USGS scientists estimate that the sea floor in the vicinity of the earthquake was uplifted by several meters. Displacement of water above the sea floor triggered the tsunami [12].
“Tsunami” is made up of two Japanese words: tsu, “harbour” and nami, “sea” [13,14]. But the term ‘harbour wave’ is misleading, since tsunami don’t just occur in harbour. The scientific definition from the Department of Geophysics at the University of Washington, USA is more informative: a tsunami is a wave train, or series of waves, generated in a body of water by an impulsive disturbance that vertically displaces the water column [15].
Tsunami waves threaten rescue and recovery operations, especially when they arrive at high height. Such waves also endanger vessels in shallow water. For these reasons, emergency managers need to know tsunami wave height to help guide rescue and recovery operations.
In this paper by dimensional analysis, important dimensionless numbers in tsunamis were obtained and studied. In addition, using these numbers, a simple equation to calculate energy of a tsunami wave and its wave height near the coast lines, was derived.
2. Tsunamis Are Shallow-Water Waves
First, what is a tsunami? A Tsunami is a series of waves that is generated when a disturbance vertically displaces the entire water column. These waves have very long wavelengths, sometimes greater than 100 km, as well as large periods of approximately an hour. In physics point of view, a tsunami is just a shallow-water gravity wave with tiny amplitude and extremely large wavelength λ. [7,11,16-18]. A wave becomes a shallow-water wave or Surface wave, when the ratio between the water depth and its wave length gets very small [19]. (When sea depth “d”, is much less than half of the wave length “λ/2”, we have a shallow-water wave or a long wave [20]).
In these waves, particles of the medium undergo a circular motion (Figure 1). Surface waves are neither longitudinal nor transverse. In longitudinal and transverse waves, all the particles in the entire bulk of the medium move in a parallel and a perpendicular direction (respectively) relative to the direction of energy transport. In a

Figure 1. A surface wave.
surface wave, it is only the particles at the surface of the medium which undergo the circular motion. The motion of particles tends to decrease as one proceeds further from the surface [21].
The speed of the wave crest, also called the phase velocity is for all harmonic waves given by the ratio of the wavelength to the period [7,22,23]:
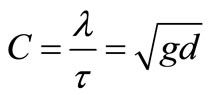 (1)
(1)
This equation clearly shows that the speed of tsunami wave corresponds to the depth of the sea, d. For example, in the Indian where the typical water depth is about 3963 m, a tsunami travels approximated to 197 m·s–1or 709 km·h–1[17,24]. The speed of tsunami in Indian Ocean is comparable to the speed of Boeing 737. This phenomenon of speed show that it may move from one side of the Indian Ocean to the other side in less than one day. Table 1 indicated the information of the depth of main world ocean with the average speed of tsunami wave [25].
3. Dimensionless Parameters in Tsunami
Dimensional analysis is a conceptual tool often applied in physics, chemistry, and engineering to understand physical situations involving a mix of different kinds of physical quantities. It is used to form reasonable hypotheses about complex physical situations that can be tested by experiment or by more developed theories of the phenomena.
The Buckingham π theorem is of central importance to dimensional analysis. This theorem describes how every physically meaningful equation involving n variables can be equivalently rewritten as an equation of n-m dimensionless parameters, where m is the number of fundamental dimensions used. Furthermore, and most importantly,

Table 1. Ocean depth information with average speed of tsunami wave [25].
it provides a method for computing these dimensionless parameters (also called dimensionless numbers) from the given variables [26].
In this study, using dimensional analysis and considering effective parameters on tsunami power, important dimensionless numbers in tsunami were obtained.
Considered parameters are as follows: wave speed (C), length of fault (L), water amplitude (a), standard gravity (g), sea water density (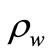 ) and wave period
) and wave period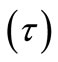 . Now we can find that we can form four dimensionless numbers.
. Now we can find that we can form four dimensionless numbers.
The four groups found can be combined into an equivalent form as an equation
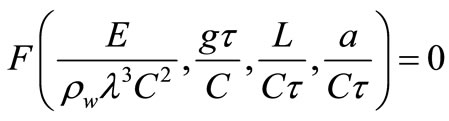 (2)
(2)
where F is some unknown function, or, equivalently as
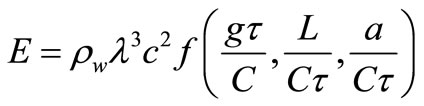 (3)
(3)
So dimensionless groups can be obtained as fallows:
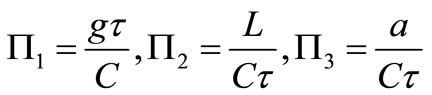 (4)
(4)
The value of 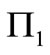 in different tsunamis is larger than 10, so required depth criteria to produce shallow water waves in tsunami simulation experiments, can be defined as:
in different tsunamis is larger than 10, so required depth criteria to produce shallow water waves in tsunami simulation experiments, can be defined as:
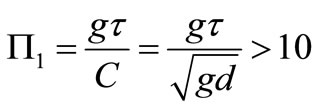 (5)
(5)
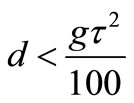 (6)
(6)
This result is in agreement with shallow water traditional criteria [24]:
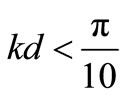 (7)
(7)
where, k and 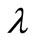 are wave number and wavelength, respectively:
are wave number and wavelength, respectively:
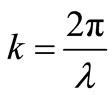 (8)
(8)
 (9)
(9)
The second non-dimensional number is Hammack number [27]:
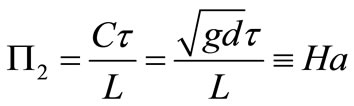 (10)
(10)
This number describes the method of generation of waves and is the ratio between the time scale of the landslide motion and the time it takes for long waves to propagate over the region in which they were generated.
The third non-dimensional number  is the ratio between the wave amplitude to wavelength and in all the tsunamis it has a very little value (
is the ratio between the wave amplitude to wavelength and in all the tsunamis it has a very little value ( ):
):
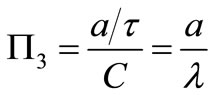 (11)
(11)
4. Energy of a Tsunami Wave
Basically, earthquake may occur from volcano eruption, meteor impacts, underground explosion (nuclear test) and movement of earth plates (tectonic). But for the Indian Ocean earthquake on December 26th 2004, have been reported that it may caused by the tectonic phenomena [11].
There exists an empirical relation, called the Gutenberg-Richter formula, between an earthquake’s magnitude and the energy that is radiated all over the globe in the form of seismic vibrations. If the energy E is measured in joule (J), the Gutenberg-Richter formula is traditionally written as [23,28]:
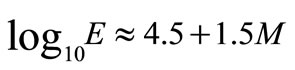 (12)
(12)
where, M is the Richter magnitude. For the Indonesian earthquake this formula yields: 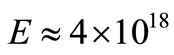 J, corresponding to the energy released in the explosion of about 500 million tons TNT.
J, corresponding to the energy released in the explosion of about 500 million tons TNT.
The power of a tsunami wave was estimated in several methods. McIntyre [29] suggested following relation to calculate power of tsunami by using Bernoulli equation:
 (13)
(13)
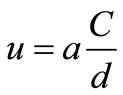 (14)
(14)
Benny Lautrup [23] and M.N.A. Halif et al. [7], obtained following relation by calculating potential energy of waves and considering ‘waterberg’ phenomena:
 (15)
(15)
By considering tsunami as a big solitary wave that propagates without dispersing its energy over larger and larger regions of space [30] (Soliton is widespread natural non-linear Phenomenon described by nonlinear partial differential equations [31]), Fr´ed´eric Dias & Denys Dutykh [32] derived following equation to estimate tsunami energy:
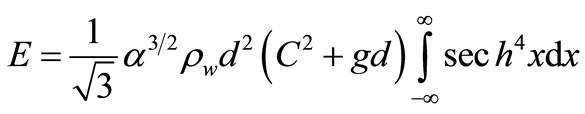 (16)
(16)
With respect to this fact that long waves dissipate very little energy (E ~ a2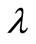 ) [23,33], the unknown function
) [23,33], the unknown function 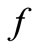 in Equation (4), can be determined. Following equation will be obtained to estimate the energy of one wavelength of tsunamis:
in Equation (4), can be determined. Following equation will be obtained to estimate the energy of one wavelength of tsunamis:
 (17)
(17)
From 2004 Indian Ocean earthquake data, L = 1200 km,  = 150 km and a = 1.5 m [7,23]. Table 2 shows a comparison among the amount of tsunami energy estimated by previous methods and the suggested equation (Equation 17).
= 150 km and a = 1.5 m [7,23]. Table 2 shows a comparison among the amount of tsunami energy estimated by previous methods and the suggested equation (Equation 17).
5. Wave height of tsunamis
All shallow-water waves move with the same speed because their velocity depends only on the depth, and a composite wave containing many harmonic components of different wave-lengths will tend to keep its shape [23]. Tsunamis not only travel at constant and great speeds but experience very limited energy loss (solitary wave). As such they can travel great distances before they dissipate [16].
But, when a tsunami wave approaches the costal region the phase velocity will decrease as c~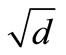 . Since there is no place that wave crests can accumulate, the period
. Since there is no place that wave crests can accumulate, the period 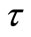 between the waves crests must be the same all the way. So, according to Equation (1), wavelength becomes shorter in the same way as the phase velocity. When the wavelength becomes comparable to the depth,
between the waves crests must be the same all the way. So, according to Equation (1), wavelength becomes shorter in the same way as the phase velocity. When the wavelength becomes comparable to the depth, 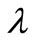 ~ d, dispersion will set in. The relevant parameter for estimating the importance of dispersion is
~ d, dispersion will set in. The relevant parameter for estimating the importance of dispersion is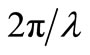 . Over long distances the dispersion will separate the wavelengths such that the very longest waves hit the coast first [23].
. Over long distances the dispersion will separate the wavelengths such that the very longest waves hit the coast first [23].
According to Equation (17), E ~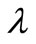 a2, by considering a tsunami wave as a soliton, the amplitude must grow as
a2, by considering a tsunami wave as a soliton, the amplitude must grow as 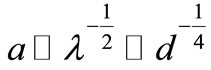 . When the amplitude becomes comparable to the depth, non-linear effects set in and may cause the wave to break and froth before it hits the beach. Here its enormous energy of about one gigajoule per meter of beach causes extensive destruction of the coastal areas.
. When the amplitude becomes comparable to the depth, non-linear effects set in and may cause the wave to break and froth before it hits the beach. Here its enormous energy of about one gigajoule per meter of beach causes extensive destruction of the coastal areas.

Table 2. A comparison among estimated energy of December 26th 2004 tsunami of Sumatra.
In general, the extent of amplitude of sea water during tsunamis depends on earthquake parameters, geographical location, velocity of tsunami waves and their frequency, near shore bathymetry, beach profile and land topography [6]. However, by using Equation (17) and substituting the required time that it takes for a tsunami wave to reach the beach in place of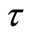 , height of tsunami waves (a), near the coastline can be estimated.
, height of tsunami waves (a), near the coastline can be estimated.
To show this, using the available information for 26 December 2004 Tsunami in Sumatra, like its energy (E) and the time that tsunami wave reach the beach ( ), a comparison between reported value of wave heights and estimated ones for this tsunami was done and its results are given in Table 3. As it can be seen from this table, there is a good agreement between estimated values and the reported ones. Also we can use Equation (17) to estimate the height of tsunami waves in other tsunamis.
), a comparison between reported value of wave heights and estimated ones for this tsunami was done and its results are given in Table 3. As it can be seen from this table, there is a good agreement between estimated values and the reported ones. Also we can use Equation (17) to estimate the height of tsunami waves in other tsunamis.
In 26 May 1983, a magnitude 7.8 Mw (USGS) earthquake in the central region of the Sea of Japan, about 80 km off the west coast of Akita Perfecture, Japan, caused 103 fatalities and 324 injuries. One hundred of the fatalities were due to the tsunami. The fault length was 120 km - 130 km running north to south with a breadth about 40 km east to west [36]. By using Equation (17), the amount of released energy can be estimated as 3.011 × 1014j. Table 4 shows comparison between reported wave’s heights and estimated ones.
In 12 Dec 1992, a magnitude 7.5 Ms (USGS) earthquake in the Flores, Indonesia region, produces a tsunami that it reached shore in five minutes. The source was a thrust fault dipping 32 degrees to the south and
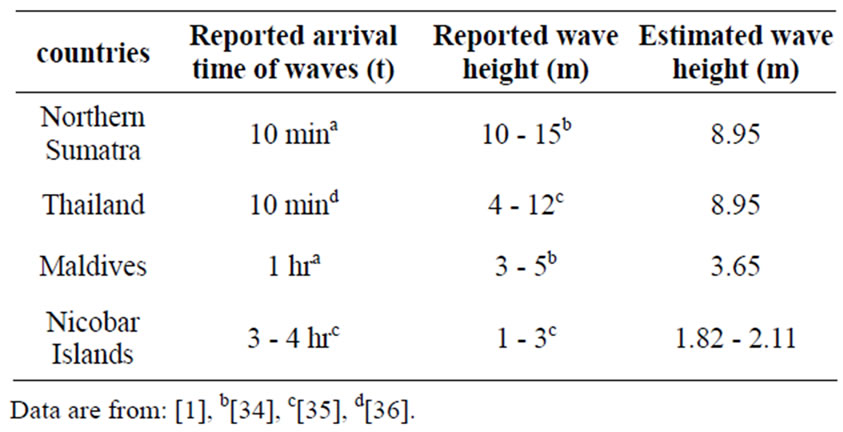
Table 3. The comparison between reported wave heights with estimated ones (26 December 2004 Tsunami).

Table 4. The comparison between reported wave heights with estimated ones (26 May 1983 Tsunami).
Table 5. The comparison between reported wave height with estimated one (12 Dec 1992 Tsunami).
extending about 110 km from Cape Batumanuk to Cape Bunga [36]. The comparison between reported wave height and estimated one is given in Table 5.
6. Conclusions
Tsunami waves are shallow-water waves with very large wavelengths, phase velocities and periods. In this work, we used dimensional analysis to obtain and study important dimensionless numbers in tsunamis. One of these numbers is  that can be used to determine the required depth criteria to produce shallow water waves in tsunami simulation experiments. Another dimensionless number
that can be used to determine the required depth criteria to produce shallow water waves in tsunami simulation experiments. Another dimensionless number  describes the method of generation of waves.
describes the method of generation of waves.
In addition, using dimensional analysis, we obtained an equation to calculate the energy of a tsunami wave and compared the result of calculation of energy released in 26 December 2004 Tsunami in Sumatra by suggested equation with pervious methods.
As mentioned earlier, when a tsunami wave reaches land, its period will remain the same as in deep waters, whereas the phase velocity and the wavelength become smaller while the amplitude grows. The net result is that the water level is raised several meters, flooding the beach and coastal areas. However, behavior of a tsunami wave near the coastline depends not only on considered parameters but also on other parameters such as coast slope and local topography. But because of lack of complete information about tsunamis, by a simple equation presented here (Equation 17), wave height can be estimated with an acceptable error as such estimated for three tsunamis and compared with reported values.
7. REFERENCES
- “The Great Earthquake and Tsunami of 26 December,” 2007. http://www.drgeorgepc.com/index.htm.
- S. Stein and E. A. Okal, “Size and Speed of the Sumatra Earthquake,” Nature, Vol. 434, 2005, pp. 580-582.
- V. V. Titov, A. B. Rabinovich, H. O. Mofjeld, R. E. Thomson and F. I. González, “The Global Reach of the 26 December 2004 Sumatra Tsunami,” Science, Vol. 309 No. 5743, 2005, pp. 2045-2048
- A. Schleicher, “Scientist Explain the Origin of South Asia’s Deadly Tsunami,” MacNeil/Lehrer Productions, Denver, 2004.
- M. N. A. Halif and S. N. Sabki, “The Physics of Tsunami: Basic Understanding of the Indian Ocean Disaster,” American Journal of Applied Sciences, Vol. 2, No. 8, 2005, pp. 1188-1193. doi:10.3844/ajassp.2005.1188.1193
- M. V. Ramanamurthy, S. Sundaramoorthy and Y. Pari, “Inundation of Sea Water in Andaman and Nicobar Islands and Parts of Tamil Nadu Coast during 2004 Sumatra Tsunami,” Current Science, Vol. 88, No. 11, 2005, pp. 1736-1740
- H. M. Fritz and J. C. Borrero, “Field Surveys of 2004 Indian Ocean Tsunami from Sumatra to East Africa”, Third Tsunami Symposium of the Tsunami Society, Honolulu, 23-25 May 2006.
- C. Lomnitz and S. Nilsen-Hofseth, “The Indian Ocean Disaster: Tsunami Physics and Early Warning Dilemmas,” Transactions American Geophysical Union, Vol. 86, No. 7, 2005, p. 65. doi:10.1029/2005EO070001
- I. Fehr , P. Grossi and S. Hernandez, “Managing Tsunami Risk in the Aftermath of 2004 Indian Ocean Earthquake & Tsunami,” 2006 Risk Management Solution ,Inc.
- “Preliminary Assessment of Impact of Tsunami in Selected Coastal Areas of India,” Department of Ocean Development Integrated Coastal and Marine Area Management Project Directorate Chennai, June 2005.
- “2004 Indian Ocean earthquake,” 2005. http://en.wikipedia.org/wiki/2004_Indian_Ocean_earthquake.
- “Indian Ocean Earthquake Triggers Deadly Tsunami”. http://soundwaves.usgs.gov/2005/01/index.html
- J. Floor Anthony, “Oceanography: Waves,” 2005. www.seafriend.org.nz/ocean/waves.htm,
- “Tsunami”, 2005. http://en.wikipedia.org/wiki/Tsunami.
- “Calculating the threat of tsunami,” 2007. http://Science .org. au//aashome.html.
- S. Loucaides, “Tsunamis: The Killer Waves,” 2003. http://rover.phy.uncwil.edu/phy475/spring02/students/Loucaides/tsunamipaper.pdf.
- “The IOC/UNESCO Indian Ocean Tsunami Post Tsunami field survey,” 2008. http://ioc.unesco.org/iosurveys/seychelles/sey2.htm.
- “Intergovernmental oceanographic commission, Tsunami information,” 2008. http://www.ioc-tsunami.org/index.php?option=com_content&task=view&id=19&Itemid=29.
- “How do tsunamis differ from other water waves?” 2007. http://www.geophys washington.edu/tsunami.htm.
- “Water Waves,” 2007. www.alaska.net/~atwc/physics.htm.
- “The Nature of a Wave,” 2007. www.glenbrook.k12.il.us/gbassci/phys/CLass/waves/u10|1c.htm|.
- A. Uy, “The Physics of Tsunamis: The Harbor Wave,” UBC Physics 420: Demonstrations. http://outreach.phas.ubc.ca/phys420/p420_05/anthony/The%20Physics%20of%20Tsunamis.htm
- B. Lautrup, “Tsunami Physics,” The Niles Bohr Institute, Copenhagen, 2005
- “Tsunami Information,” 2007. http://www.bom.gov.au/index.shtml.
- “Earth’s Ocean: An introduction,” 2005. http://www.enchantedlearning.com/subjects/ocean/.
- “Dimensional analysis,” 2008. http://en.wikipedia.org/wiki/Dimensional_analysis.
- P. Watts, “Tsunami Features of Solid Block Underwater Landslides,” Journal of Waterway, Port, Coastal and Ocean Engineering, Vol. 126, No. 3, 2000, pp. 144-152. doi:10.1061/(ASCE)0733-950X(2000)126:3(144)
- R. Gutenberg, B. and C. F. Ritcher, “Seismicity of the Earth and Associated Phenomenon”, 2nd Edition, Princeton University Press, Princeton, 1954.
- M. E. McIntyre, “Tsunami”
- Answer.com, 2008. http://www.answers.com/topic/soliton?cat=technology.
- V. Sergey, J. Biryukov, Fydorova, “Tsunami in DERIVE and TI-92,” (The Workshop “Studding Solitons”)
- F. Dias and D. Dutykh, “Dynamic of Tsunami Waves,” Ecole Normale Sup´erieure de Cachan, Springer, New York, 2006.
- “Properties of Waves,” 2007. www.glenbrook.k12.il.us/gbassci/phys/CLass/waves/u10|2c.htm|.
- J. Marshall, “2004 Sumatra Earthquake & Indian Ocean Tsunami,” Geological Sciences Department Cal Poly Pomona University, Pomona.
- G. Weber, “Earthquake and Tsunami maps, charts and sequence of events,” 2008. http://www.andaman.org/mapstsunami/tsunami.htm.
- J. F. Lander, L. S. Whiteside, P. A. Lockridge, “Two Decades of Global Tsunamis 1982-2002,” Vol. 21, No. 1, 2003, p. 3.
Nomenclature
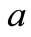 Water amplitude (m),
Water amplitude (m),
 Wave speed (m·s–1),
Wave speed (m·s–1),
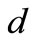 Water depth (m),
Water depth (m),
 Power (j),
Power (j),
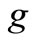 Standard gravity (m·s–2),
Standard gravity (m·s–2),
Ha Hammack number (-),
L length of fault (m),
U Horizontal speed (m·s–1),
Greek symbols
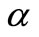
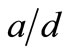 Ratio (-),
Ratio (-),
 Wave period (s),
Wave period (s),
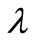 Wavelengths (m),
Wavelengths (m),

