Engineering
Vol. 3 No. 3 (2011) , Article ID: 4145 , 4 pages DOI:10.4236/eng.2011.33028
Comparison of Wind-Induced Displacement Characteristics of Buildings with Different Lateral Load Resisting Systems
1Department of Civil Engineering, The Federal University of Technology, Akure, Nigeria
2Works Department, Ladoke Akintola University of Technology, Ogbomoso, Nigeria
E-mail: arumcnwchrist@yahoo.co.uk, engr.akinkunmi@gmail.com
Received December 25, 2010; revised January 5, 2011; accepted January 17, 2011
Keywords: Moment Frame, Shear Wall, Dual System, Inter-Storey Drift, Lateral Displacement, Wind Load
ABSTRACT
Due to excessive displacements of tall buildings occasioned by lateral loads, lateral load resisting systems are usually provided to curtail the load effect. The resistance may be offered by Frame Action, Shear Walls, or combined Walls and Frames (also known as Dual System). In this study, finite element based software, ETABS, was used to generate and analyse three-dimensional building models for the assessment of the relative effectiveness of the various lateral load resisting systems. Three models were used, one each for the three resisting systems. Each model consisted of three samples representing three different building heights of 45 m, 75 m, and 99 m. Wind Design Spreadsheet complying with the appropriate British Standards was used to compute preliminary wind load coefficients using the wind speed values from the relevant wind isopleth map of Nigeria as primary data. Lateral wind load was then applied at floor levels of each of the building samples. Each building sample was subjected to three-dimensional analysis for the determination of both the lateral displacements of storey tops and interstorey drifts. The results of the work showed that the dual system was the most efficient lateral-load resisting system based on deflection criterion, as they yielded the least values for lateral displacements and inter-storey drifts. The moment frame was the least stiff of the resisting systems, yielding the highest values of both the lateral displacement and the inter-storey drift.
1. Introduction
In general, as the height of a building increases, its overall response to lateral load (such as wind and earthquake) increases. When such response becomes sufficiently great such that the effect of lateral load must be explicitly taken into consideration in design, a multistory building is said to be tall. Tall buildings are prone to excessive displacements, necessitating the introducetion of special measures to contain these displacements. The lateral load effects on buildings can be resisted by Frame action, Shear Walls, or Dual System. Peak interstorey drift and lateral displacement (or sidesway) are two essential parameters used for assessing the lateral stability and stiffness of lateral force resisting systems of tall buildings.
Park, Hong & Seo [1] in their work pointed out that the efficiency of lateral load resisting system or the amount of materials required for multistorey buildings heavily depends on drift limits. Kowalczyh [2] noted the difficulties faced by Structural Engineers in selecting strong and stiff enough deformation resisting systems that will curtail the drift within acceptable code limits. Chen & Lui [3] extensively discussed susceptibility of multistorey buildings to sway under lateral wind loading and therefore advocated the need for good understanding of the nature of wind load and estimation of interstorey drift. Sindel et al. [4] reiterated the importance of the knowledge of lateral displacements at the top of multistorey buildings because of its usefulness in assessing the stability and stiffness of multistorey buildings.
In view of the foregoing, this study examined the three deflection limiting structural systems (moment frame, shear-wall and dual system) prominently utilized in tall building structures, in order to establish their relative effectiveness.
2. Lateral Load Resisting Systems
2.1. Shear Wall System
Khajehpour [5] described Shear Walls as stiff structures with high ductility which keeps the deformations of non-ductile framing systems in the elastic range. He noted that the in-plane load resistance is the principal strength of shear walls and that the resistance against both gravity and lateral loads can be assigned to shear walls if they are appropriately located in a building.
2.2. Moment Frame System
Moment Frame is suitable where the presence of Shear Wall is undesirable, especially in situations where architectural limitation is imposed. The results of Khajehpour’s work [5] revealed that Moment Frame is economical up to twenty stories while Smith & Coull [6] submitted that it is economical for buildings up to twenty-five stories, above which their behaviour is costly to control.
The lateral deflection of Moment Frame is caused by two modes of deformation, namely chord drift which accounts for 20% of the total drift of structures, and frame racking which accounts for 80% of the storey drift [5].
2.3. Dual Frame-Wall System
Gardiner, Bull, and Carr [7] in their work noted that the wall element in dual system is responsible for an increase of stiffness which is beneficial in terms of drift control. Nawy [8] observed that if they were to act independently, the shear walls would deflect as vertical cantilevers with greater interstorey drift occurring at the top while the frames would deflect at more uniform rate or with greater interstorey drift at the bottom. With rigid diaphragms he noted that there is a forced compatibility of frame and wall deflection at each storey and this induces interaction forces between shear walls and frames. He showed that the pattern of these forces is such that the shear walls tend to support the frame at the lower stories and the frame tends to support the shear walls at the upper stories.
3. Wind Load Determination
Lungu and Rackwitz [9] in their studies established that wind effects on buildings and structures depend on the general wind climate, the exposure of buildings, type of structures and their elements, the dynamic properties, and the shape and dimensions of the building structure. BS6399-2 [10] is the widely adopted code for wind load estimation in Nigeria. For the computation of wind loads, the Standard Method was employed. The static approach used in this study is based on a quasi-steady assumption equivalent to a structure that is dynamically displaced in its lowest frequency mode and assumes a building to be a fixed rigid body in the wind direction. According to BS 6399-2 [10], the site wind speed is given by the following formula:
 (1)
(1)
where:
Vb = basic wind speed;
Sa = altitude factor;
Sd = wind direction;
Ss = seasonal factor; and Sp = probability factor.
According to the Code [10], the effective wind speed is computed as follows:
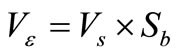 (2)
(2)
where:
Sb = terrain and building factor.
The dynamic pressure is obtained as follows:
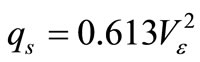 (3)
(3)
and the net load, P, on an area of a building element is given as the product of net pressure across the surface p, and the loaded area A, as given by Equation (4).
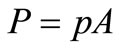 (4)
(4)
where:
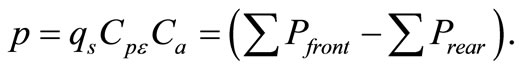
Here:
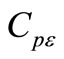 = net pressure coefficient;
= net pressure coefficient;
Ca = size effect factor;
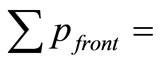 horizontal component of surface load summed over the windward-facing walls and roofs, and
horizontal component of surface load summed over the windward-facing walls and roofs, and
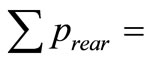 horizontal component of surface load summed over the leeward-facing walls and roofs.
horizontal component of surface load summed over the leeward-facing walls and roofs.
A basic wind speed of 56 m/s was employed in this work, the maximum value for Nigeria.
4. Storey Drifts Limitation
Sindel et al. [4] defined the storey drift as the difference of maximum lateral displacements of any two adjacent floors under the factored loads, divided by respective storey height. In terms of elastic deflections, the storey drift, S is given by
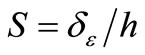 (5)
(5)
 (6)
(6)
where:
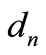 = maximum elastic deflections of the nth floor under the factored loads.
= maximum elastic deflections of the nth floor under the factored loads.
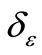 = difference of the elastic deflections between two neighbouring floors.
= difference of the elastic deflections between two neighbouring floors.
h = storey height .
BS 8110-2 [11] restricts relative lateral deflection in any one storey under the characteristic wind load to a maximum of![]() ; where H is the storey height. Higher values of storey drift limitation
; where H is the storey height. Higher values of storey drift limitation 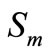 are permitted to vary between 0.004 and 0.008 when the non structural elements are isolated from and not integrally connected to the main structure. Sindel et al. [4] had proposed that the upper limit of the elastic storey drift could be taken as
are permitted to vary between 0.004 and 0.008 when the non structural elements are isolated from and not integrally connected to the main structure. Sindel et al. [4] had proposed that the upper limit of the elastic storey drift could be taken as
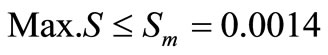 (7)
(7)
5. Modeling Assumptions and Idealizations
The following assumptions apply in this work:
1) Static or equivalent static loads as recommended by BS 6399-2 [10] are considered.
2) Dead loads are assumed to be invariant with changes in member sizes.
3) The material of concrete is assumed to be linearly elastic and P-∆ effects are not considered.
4) Structural members are straight and prismatic.
5) In order to reflect actual behaviour of structures, all frames are assumed to be rigid in plane, hence they constrain the horizontal shear deflection of all vertical bents at floor levels to be related by the horizontal translations and floor slab rotations.
6) All connections between members of all building models are assumed rigid while the buildings are fixed at the base.
7) The buildings are assumed to be office complex type meant for general use located in exposure B.
8) Member sizing is carried out based on the provision for worst combination of load forces as stipulated by BS 8110-1 [12].
9) It is assumed that window openings are installed in all shear walls at 1.0 m above floor levels with total width of 2.60 m and stretch to a height of 1.2 m while the door openings 2.10 m high by 1.2 m wide are introduced at the floor levels.
10) Major axis is taken to be the axis about which the section has the larger second moment of area.
11) The wall piers of wall-frame structures are uniform.
6. Materials and Methods
Finite Element Method of analysis was employed in the structural modeling of all three lateral load resisting systems. This was achieved by the use of both Wind Design Workbook by Buczkowski [13] and ETABS computer analysis software package.
6.1. Generation of Building Analytical Models
Three building models were generated with the aid of ETABS, representing the three lateral load resisting systems under investigation. Each model consisted of three building samples which differed only by the number of storeys, namely, 15, 25 and 33 storeys. Thus, nine samples altogether were generated, loaded and their threedimensional analyses were performed using ETABS software. Each sample had four bays in the X direction and three bays in the Y direction. The storey height was fixed at 3.0 m. The bay width was 5 m centre-to-centre equal span in both X and Y directions. This brought the overall plan dimensions of the building to 20.0 m by 15.0 m. The general arrangement drawings for typical floors for the moment frame, the shear wall system and the dual system are shown respectively in Figures 1, 2 and 3.
In the moment resisting frame (Figure 1), every joint is an intersection of beams and columns and it is this network of beams and columns that resists the lateral load by the bending action of the members. In the shear wall building (Figure 2), the interior of the building framework consists of beams and columns while the exterior frame of the building consists of shear walls and beams without any columns. Finally, the dual system (Figure 3) has columns and beams both within the interior and the exterior framing of the building but in addition
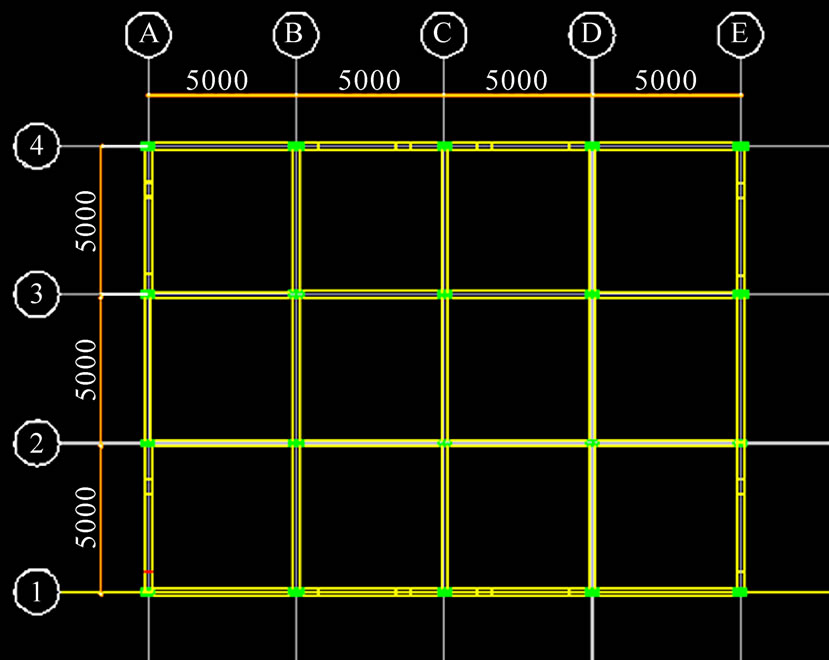
Figure 1. General arrangement drawing for a typical floor for the moment frame.
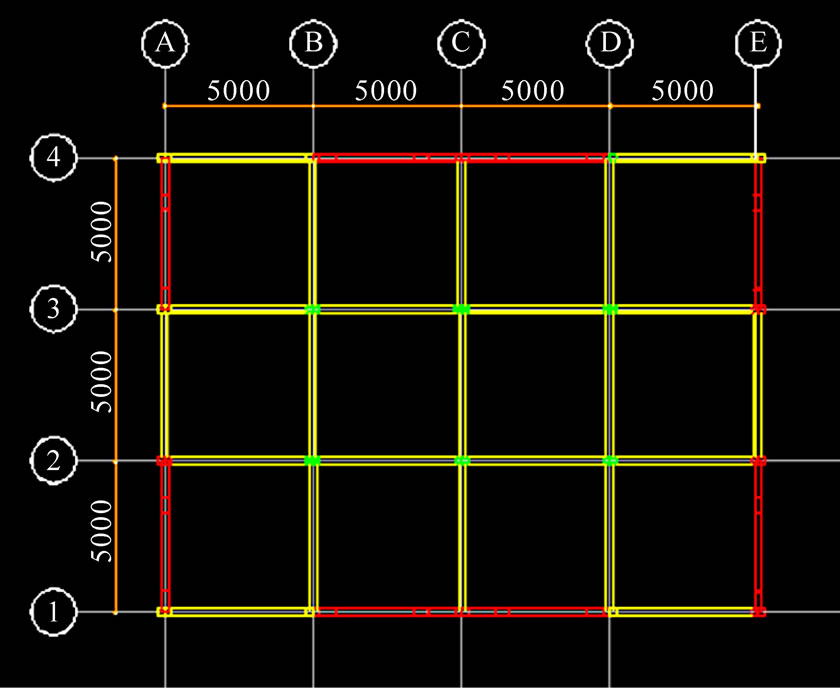
Figure 2. General arrangement drawing for a typical floor for the shear wall system.
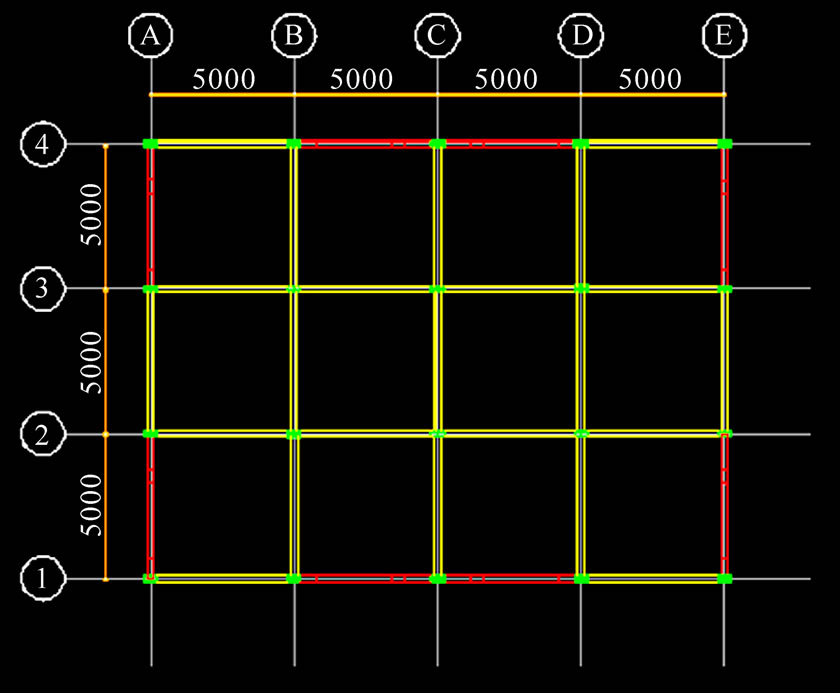
Figure 3. General arrangement drawing for a typical floor for the dual system.
it also has shear walls incorporated in the exterior framework of the building.
A typical three-dimensional model with shear wall is shown in Figure 4 for a 15-storey sample while Figure 5 shows the maximum nodal values of the wind load for the same model, on a plane elevation.
Every building model was assigned fixed bottom support condition while a rigid diaphragm constraint was allotted to both slab and deck members. Each model was loaded with gravity loading in addition to wind load.
6.2. Loading
The basic wind speed was obtained from the map of wind speed isopleths for Nigeria. In order to fully consider local conditions, the works of Arum [14] and Auta
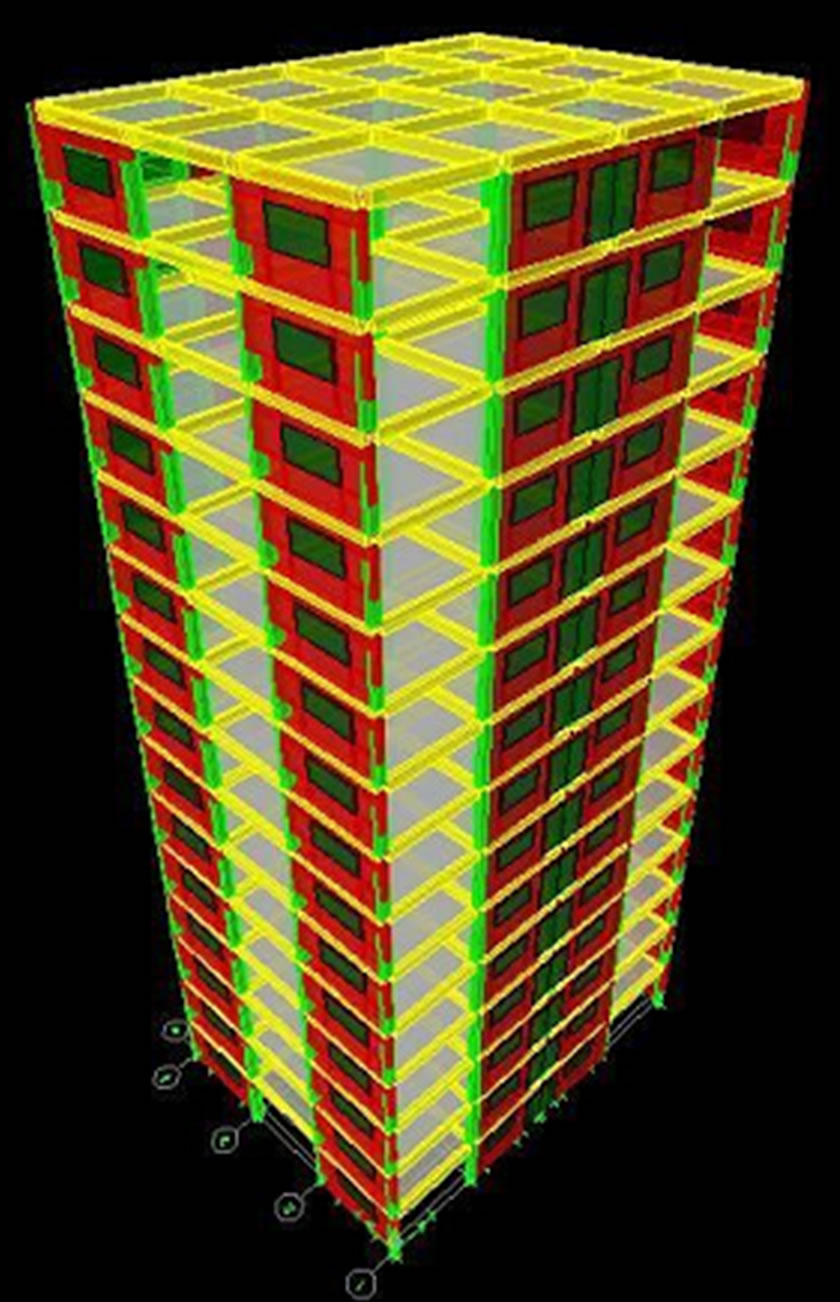
Figure 4. Typical 3D model with shear wall for the 15-storey building sample.
[15] were utilised. Wind Design Workbook developed by Buczkowski [13] which implements the full Standard Method of calculating wind loads for buildings in accordance with BS 6399-2 [10] was employed to compute the preliminary wind load which were later used as secondary wind data in ETABS software. Wind load was computed for each of the four sides of each building sample. A uniform shell live load of 2.5 kN/m2 was assigned to the solid slab along the negative global Z-direction. A live load reduction was effected on the total distributed imposed shell loads in compliance with minimum imposed floor load stipulated by BS 6399-1 [16] for office buildings. The dead load for both slab and filled deck were automatically generated by ETABS. In addition, a minimum imposed load of 1.5 kN/m2 was assigned to the deck in accordance with BS 6399 [15].
Static Load Combinations
Each of the nine samples was subjected to load combination as provided for in BS 8110-1 [12]. The load combinations included the following:

Figure 5. Maximum nodal values of the wind load for the 15-storey build-ing sample.
1) 1.4DL + 1.4WL, and
2) 1.2DL + 1.2LL + 1.2WL combinations.
where
DL = Dead load
WL = Wind load
LL = Live load
7. Results & Discussion
7.1. Results
The results of the lateral displacements curve for the 15-storey building sample, which is typical of all building heights considered, are presented in Figure 6 while their corresponding interstorey drifts are shown in Figure 7.
The values of the lateral displacements and their comparisons for the three lateral load resisting systems are shown in Tables 1 to 3 respectively for the 15-storey, 25-storey and 33-storey buildings.
The values of the inter-storey drifts as well as the comparison of the values for the three lateral load systems are shown presented in Tables 4, 5 and 6 respectively for the 15-storey, 25-storey and 33-storey buildings.
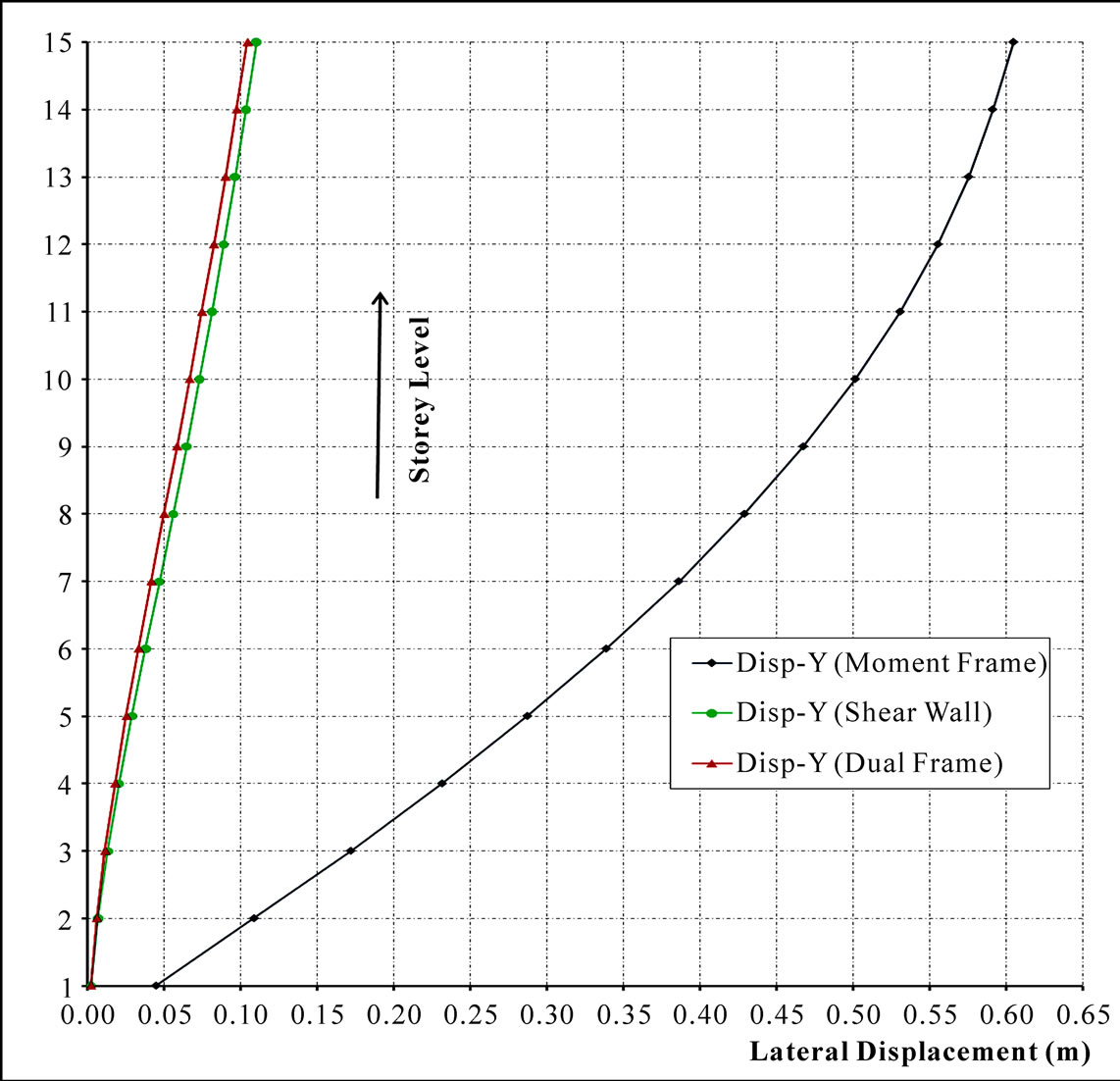
Figure 6. Lateral displacements curve for the 15-storey building sample.
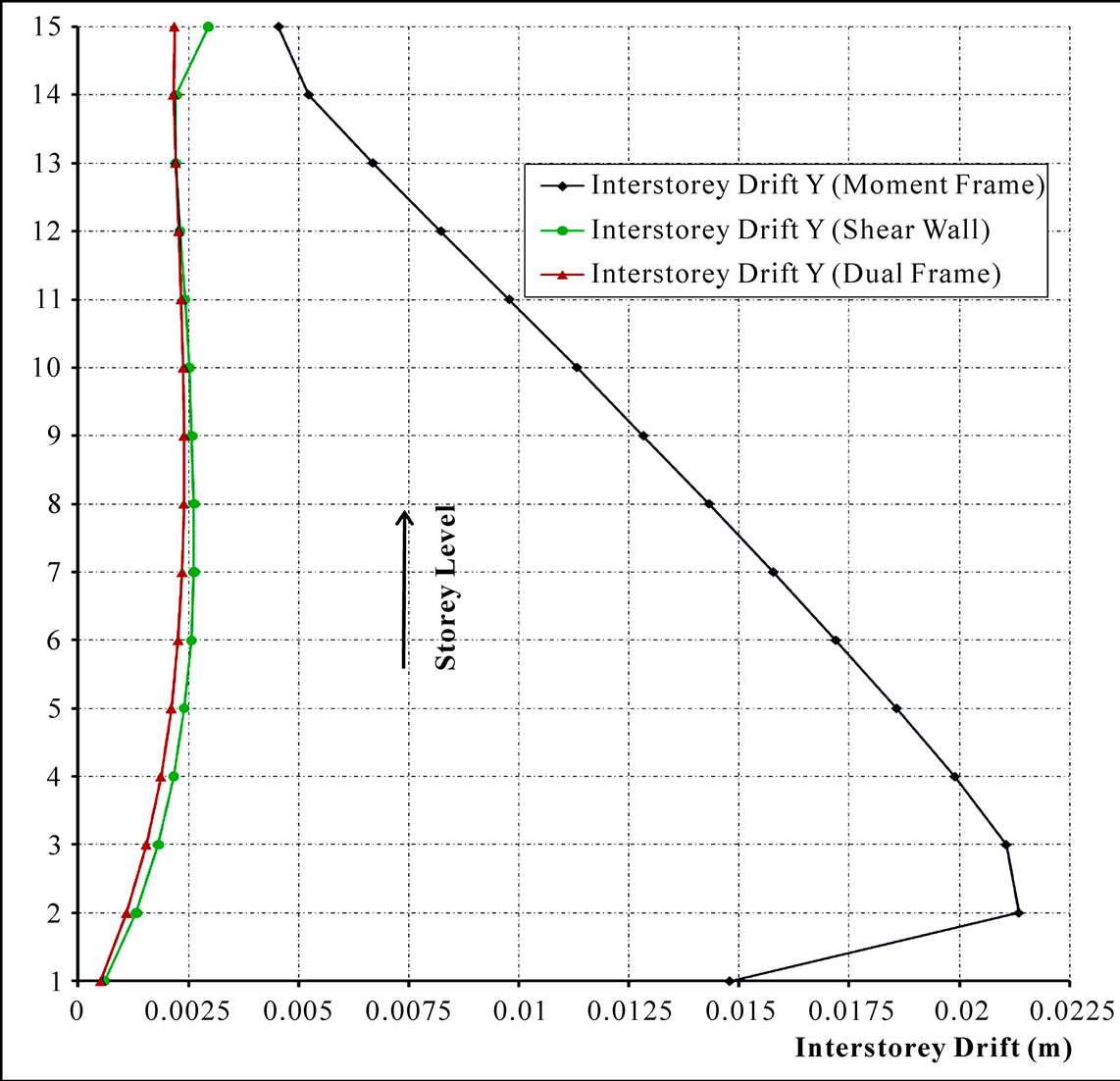
Figure 7. Inter-storey drifts curve for the 15-storey building sample.

Table 1. Comparison of lateral displacements for a 15-storey building with different lateral load resisting systems.
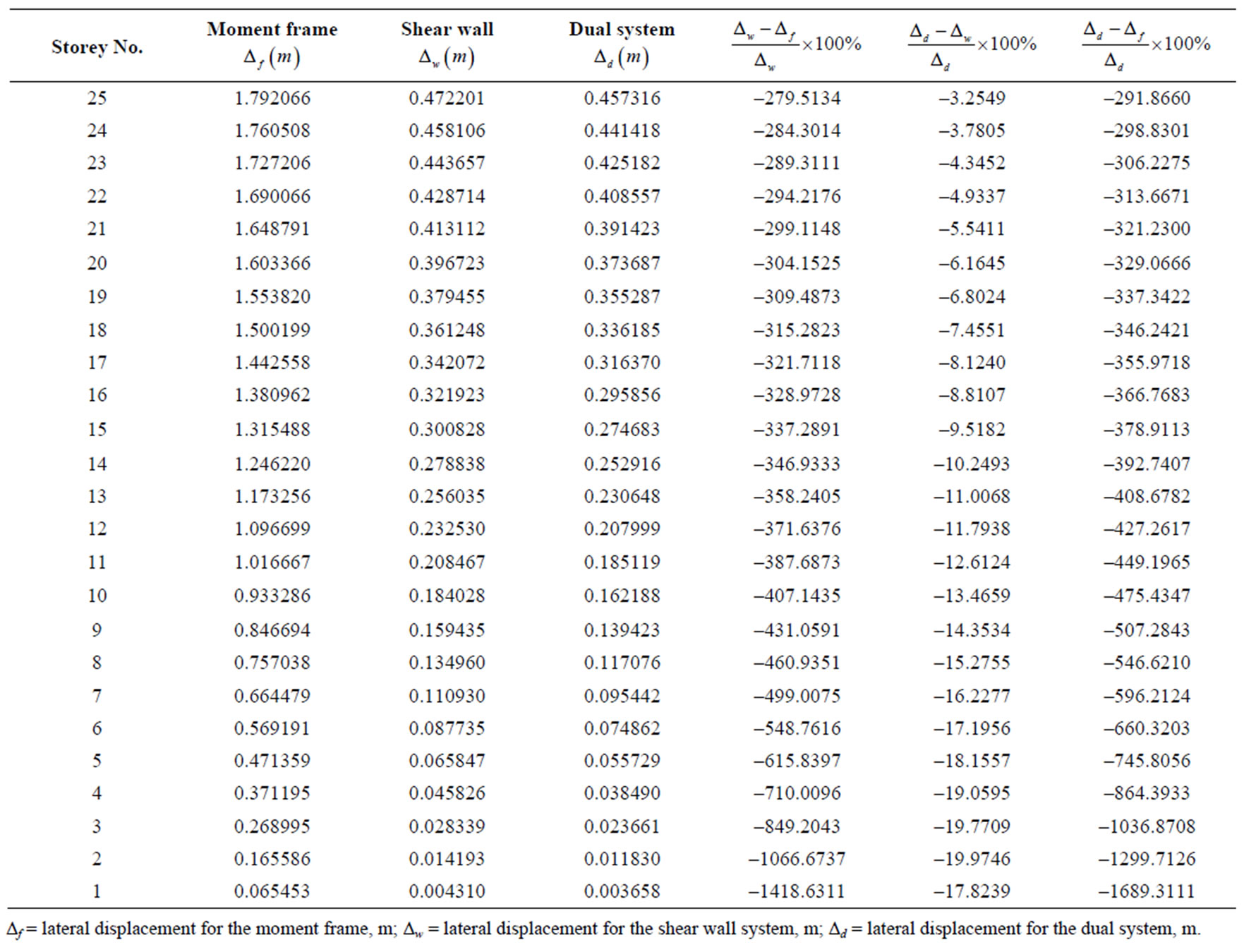
Table 2. Comparison of lateral displacements for a 25-storey building with different lateral load resisting systems.
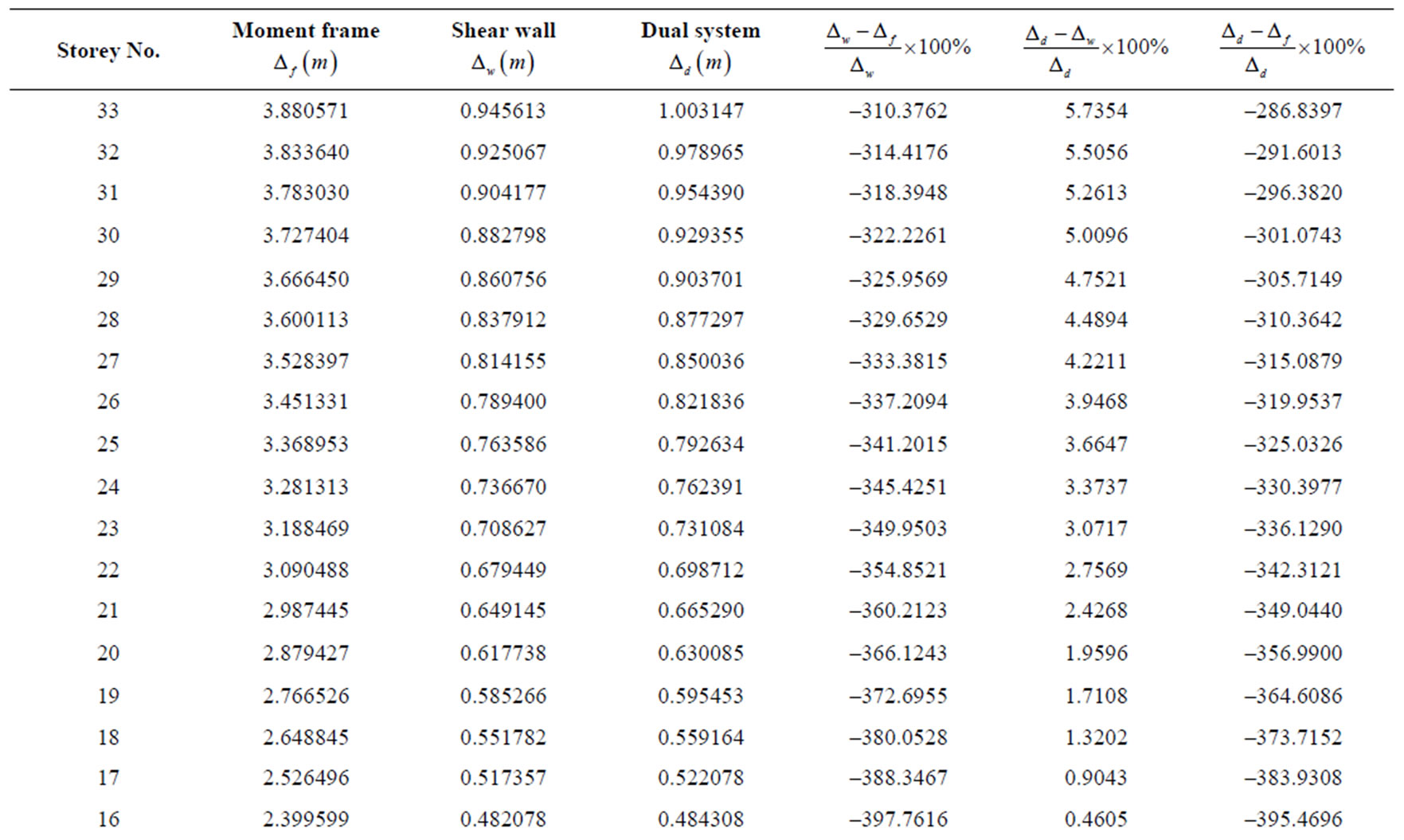

Table 3. Comparison of lateral displacements for a 33-Storey building with different lateral load resisting systems.
7.2. Discussion
A comparison of the values for the lateral displacements as contained in Tables 1, 2 and 3 for 15-storey, 25-storey and 33-storey buildings respectively shows that the lateral displacement is greatest at the topmost storeys for the three lateral force resisting systems, having the greatest values for the moment frame and the least for the dual system. For the 15-storey building, the lateral displacement of the moment frame at the level of the 1st storey is about 20 times greater than that of the shear wall system and about 24 times that of the dual system. Thus, from the standpoint of resistance to lateral displacement, the moment frame is the worst while the dual system is the best. The shear wall lies in-between being far better than the moment frame and marginally

Table 4. Comparison of inter-storey drifts for a 15-storey building with different lateral load resisting systems.

Table 5. Comparison of inter-storey drifts for a 25-storey building with different lateral load resisting systems.
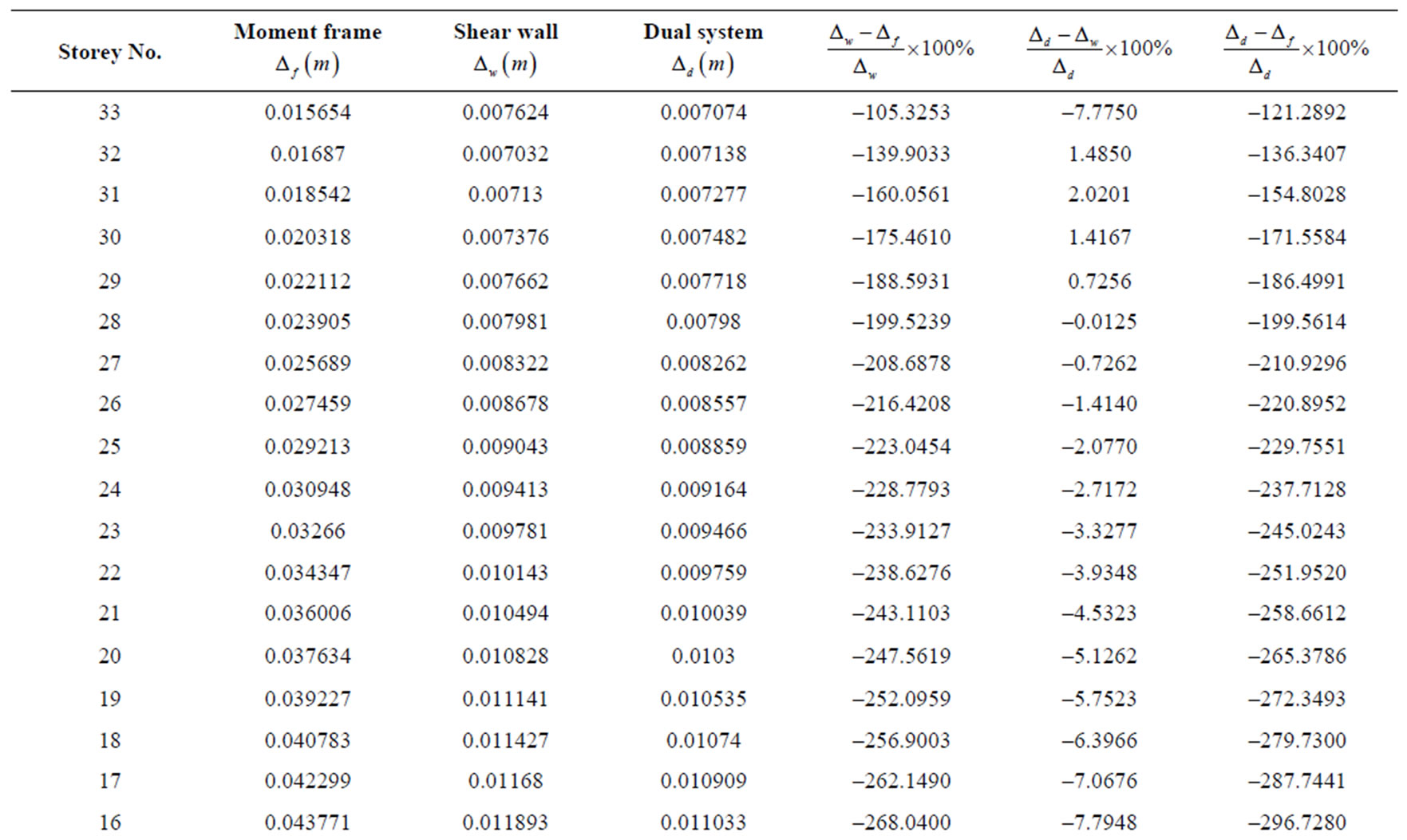
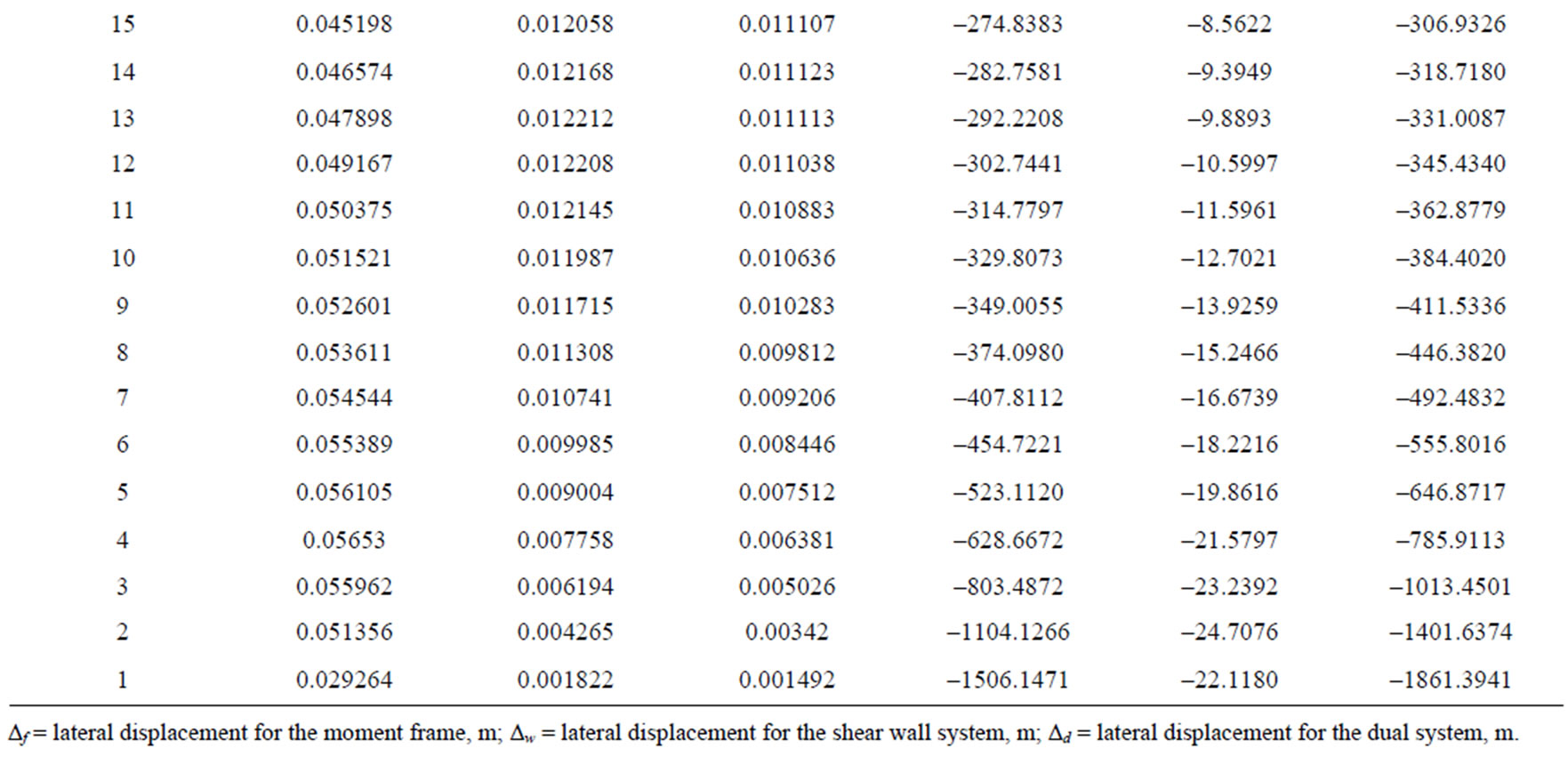
Table 6. Comparison of inter-storey drifts for a 33-storey building with different lateral load resisting systems.
worse than the dual system. In the moment resisting frame system, since the stiffness of the columns is comparable to that of the beams, the beam-column joints rotate as well as translate laterally and the high deformation components of rotation and translation sum up to give high displacement values. In the case of the shear wall system, the shear walls act like deep beams which are much stiffer than the columns. In this case the deformation due to rotation of the joints is significantly reduced and the major component of the deformation is due to lateral translation, resulting in overall reduced lateral displacement values. Finally, since the dual system incorporates both columns and beams as well as shear walls, the system is the stiffest of the three and the extra resistance offered by the periphery columns further reduces the lateral displacement prevailing in the case of the shear wall system. In practice, in order to reach a decision on which of the shear wall and the dual system to use, the extra stiffness offered by the dual system should be weighed against the extra cost in material and construction of the periphery columns and beams, which are absent in the shear wall system.
As shown in Tables 4 to 6, for all storey variants considered, the inter-storey drift is greatest for moment frame and least for dual system. Furthermore, for all storey variants, the greatest inter-storey drifts for the moment frame occur at the lowest third along the building height, with the exception of the first storey which has about half the drift value of the average value of the storeys located in the lowermost third of the building height. For the shear wall and the dual system, the drift is greatest for the storeys located within the middle third of the building height. In addition, for the 25 and 33 storeys, whereas the drift is greater in the shear wall than for the dual system at the lower floors, from the 20th to the 24th storey for the 25-storey building and from the 29th storey to the 32nd for the 33-storey building, the drift of the dual system is greater than for the shear wall. It should be noted that this reversal occurred only for the tall buildings (25 and 33 storeys) and not for the 15-storey variant. The implication of this is that for tall buildings, there exists a height for every building from which greater building stiffness would be achieved by employing shear wall system rather than dual system.
Furthermore, the lateral displacement curves of Figure 6 show that for the moment frame, the lateral displacement increases rapidly from the first storey to about two-thirds of the building height from where the increase with height begins to dampen. The average slope of the curve within the first two-thirds of the building height is very gentle. For the shear wall and dual systems, the relationship between building height and lateral displacement is almost linear with a steep slope.
8. Conclusions
From the results of this work the following conclusions are apt:
1) The lateral displacement in moment frames is the greatest among the three lateral load resisting systems investigated; the lateral displacement in dual frames is the least while the lateral displacement in shear wall systems is slightly higher than that of the dual system.
2) Interstorey drift is greatest in moment frames and least in dual systems while that of the shear wall system is slightly higher than that of the dual system.
3) Among the building samples studied, the greatest interstorey drift occurred at the bottom third of the moment frames. For the shear wall and the dual system, the drift is greatest for the storeys located within the middle third of the building height. In addition, for the 25 and 33 storeys, whereas the drift is greater in the shear wall than for the dual system at the lower floors, from the 20th to the 24th storey for the 25-storey building and from the 29th storey to the 32nd for the 33-storey building, the drift of the dual system is greater than for the shear wall.
9. REFERENCES
- H. S. Park, K. Hong and J. Seo, “Drift Design of SteelFrame Shear-Wall Systems for Tall Buildings,” The Structural Design of Tall Buildings, Vol. 11, No. 1, 2002, pp. 35-49. doi:10.1002/tal.187
- R. Kowalczyh, “Tall Buildings: Past, Present & Future Developments,” URE: Summer School Urban Steel Structures, Gdansk, 2005.
- W. Chen and E. M. Lui, “Principles of Structural Design,” CRC Press Taylor & Francis Group, London, 2006.
- Z. Sindel, R. Akbas and S. Tezcar, “Drift Control & Damage in Tall Buildings,” Engineering Structures, Vol. 18, No. 12, 1996, pp. 959-962. doi:10.1016/0141-0296(95)00215-4
- S. Khajehpour, “Optimal Conceptual Design of HighRise Office Buildings,” Ph.D. Thesis, University of Waterloo, Ontario, 2001.
- B. S. Smith and A. Coull, “Tall Building Structures: Analysis & Design,” John Wiley & Sons, Inc., New York, 1991.
- D. R. Gardiner, D. K. Bull and A. J. Carr, “Internal Forces of Concrete Floor Diaphragms in Multistorey Buildings,” Department of Civil Engineering, University of Canterbury NZSEE Conference, Christchurch, 2008.
- E. G. Nawy, “Concrete Construction Engineering Handbook,” CRC Press, Taylor & Francis Group, London, 2008.
- D. Lungu and R. Rackwitz, “Joint Committee on Structural Safety, Probabilistic Model Code Part 2: Loads,” Joint Committee on Structural Safety, Section 2.13 on WINDS, Tampa, 1997.
- British Standards Institution, “BS 6399: Loading for Buildings—Part 2: Code of Practice for Wind Loads,” British Standards Institution, London, 1997.
- British Standards Institution, “BS 8110: Structural Use of Concrete—Part 2: Code of Practice for Special Circumstances,” British Standards Institution, London, 1985.
- British Standards Institution, “BS 8110: Structural Use of Concrete—Part 1: Code of Practice for Design & Construction,” British Standards Institution, London, 1997.
- C. Buczkowski, “Wind Design Workbook for Microsoft Excel—Version 2.1,” 2009. http://www.structural-engineering.fsnet.co.
- C. Arum, “Lightweight Steel Frameworks for Shed Buildings in Different Wind Regions of Nigeria,” Nigerian Journal of Industrial and Systems Studies, Vol. 1, No. 4, 2002, pp. 5-14.
- S. M. Auta, “Wind Load Estimation on Tall Building: Part 1: Comparison of Russian & Nigerian Codes of Practice,” Asian Journal of Civil Engineering (Building & Housing), Vol. 7, No. 3, 2006, pp. 233-238.
- British Standards Institution, “BS 6399: Loading for Buildings—Part 1: Code of Practice for Dead and Imposed Loads,” British Standards Institution, London, 1996.

