Engineering
Vol. 3 No. 7 (2011) , Article ID: 6431 , 6 pages DOI:10.4236/eng.2011.37085
Extended Finite Element Modeling: Basic Review and Programming
University of Bechar, Bechar, Algeria
E-mail: numelab@yahoo.fr
Received November 2, 2011; revised June 8, 2011; accepted June 20, 2011
Keywords: X-FEM, Programming, Fracture, Cracks, LSM
ABSTRACT
In this work, we have exposed a recent method for modeling crack growth without re-meshing. The main advantage of this method is its capability in modeling discontinuities independently, so the mesh is prepared without any considering the existence of disconti-nuities. The paper covers the formulation and implementation of XFEM, and discusses various aspects of the approach (enrichments functions, level set representation, numeri-cal integration…). Numerical experiments show the effectiveness and robustness of the XFEM implementation.
1. Introduction
The method finite element is widespread in applications of industrial design, and much of various software packages based on techniques of FEM were developed. It proved appropriate for the study of the fracture mechanics. However, modelling the propagation of a crack by a finite element mesh proves to be difficult because of the topology alteration of the mesh. Besides, the singularity of the crack end has to be represented exactly by the approximation [1].
Recently a new class has been proposed that simulates the singular nature of discrete models within a geometrically continuous mesh of finite elements. The extended finite element method XFEM has emerged from this class of problems, and is based on the concept of partition of unity for enriching the classical finite element approximation to include the effects of singular or discontinuous fields around a crack [2]. An overview of the early developments of the X-FEM method has been given by Abdelaziz [3,4].
2. Basic Works
The method of X-FEM originators were Belytschko and Black [2]. They introduced a method to develop the finite approximations element so that problems of the crack progression could be solved with remeshing minimal. Dolbow et al. [5] and Moes et al. [6] came up with a more clever technique by adapting an enrichment including asymptotic at the field and a Heaviside function of H(x).
A significant advance of the extended finite element method was given by its coupling with level set methods (LSM): The LSM is employed to represent both the crack position and that of the crack ends. The X-FEM is employed to calculate the fields of stress and displacement that is important to determine the crack growth ratio [7].
The results of the X-FEM method have been so encouraging that some authors have immediately seized the opportunity to apply this method for solving many kinds of problems where disconti-nuities and moving boundaries are to be modeled.
3. Key Ideas
3.1. X-FEM Approximation
In the X-FEM method, a standard displacement based finite element approximation is enriched by additional functions using the framework of partition of unity (Figure 1).
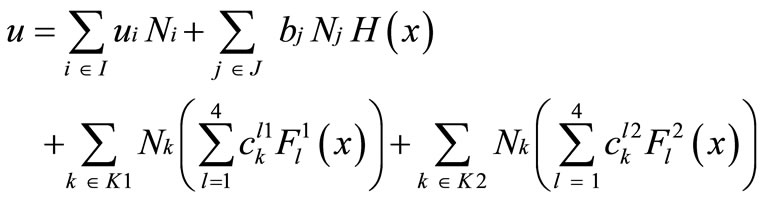 (1)
(1)
where
• Ni is the shape function associated to node i
• I is the set of all nodes of the domain
• J is the set of nodes whose shape function support is cut by a crack
• K is the set of nodes whose shape function support contains the crack front
• ui are the classical degrees of freedom (i.e. displacement) for node i
• bj account for the jump in the displacement field across the crack at node j. If the crack is aligned with the mesh, bj represent the opening of the crack
• H(x) is the Heaviside function
• ckl are the additional degrees of freedom associated with the crack tip enrichment functions Fl
• Fl is an enrichment which corresponds to the four asymptotic functions in the development expansion of the crack tip displacement field in a linear elastic solid (Figure 2).
3.2. Tip Element
The nodes whose the corresponding shape function support contains the crack tip are enriched by singular functions that can model the singular behavior of the displacement field at the crack tip.
The crack tip enrichment functions in isotropic elasticity Fi(r, q) are obtained from the asymptotic displacement fields:
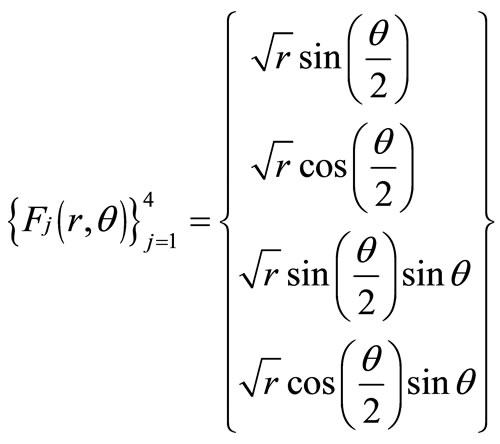 (2)
(2)
Note that the third singular function F3 is the only enrichment function which is discontinuous across the crack. Thus, the discontinuity of the displacement field at  in the singular enrichment zone is only modeled by F3 on the element containing the crack tip.
in the singular enrichment zone is only modeled by F3 on the element containing the crack tip.
3.3. Split Element
The nodes whose the corresponding shape function support is totally cut by the crack, are enriched by an Heaviside function (Figure 3).
The function of Heaviside jump is a discontinuous function through the surface of slit and constant on both slit sides: +1 on a side and –1 on the other.
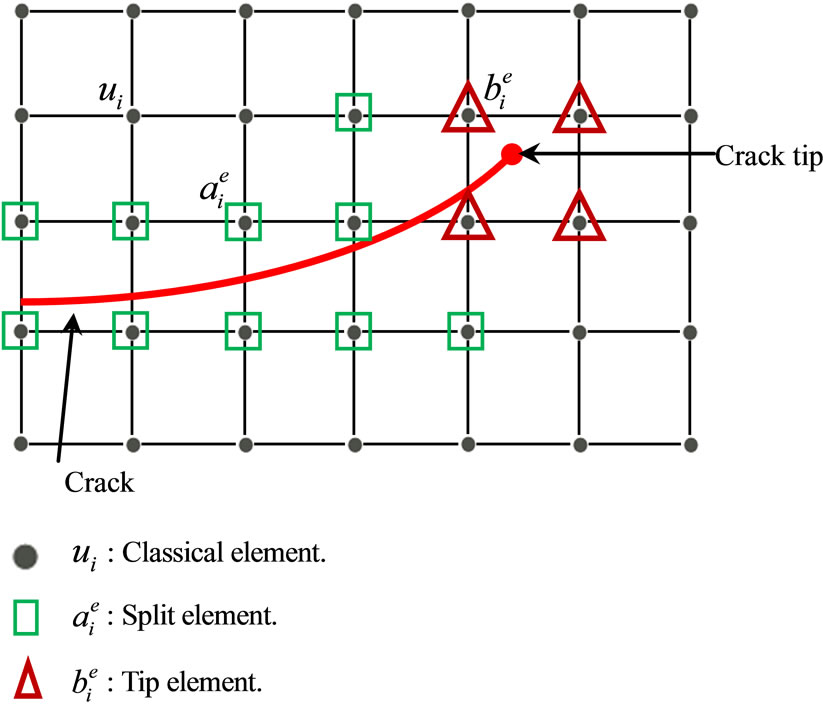
Figure 1. X-FEM enrichment strategy.
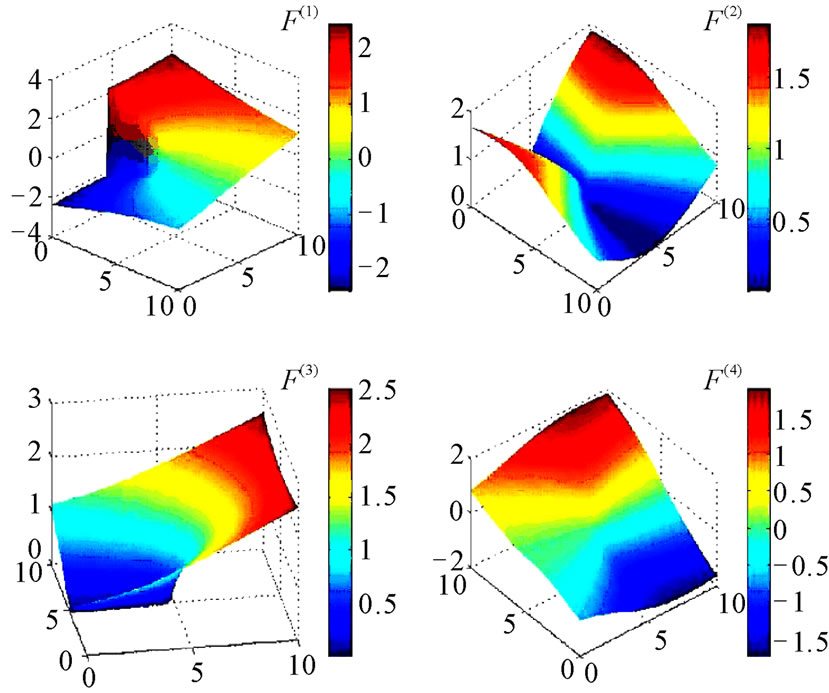
Figure 2. 2D view of near tip asymptotic functions.
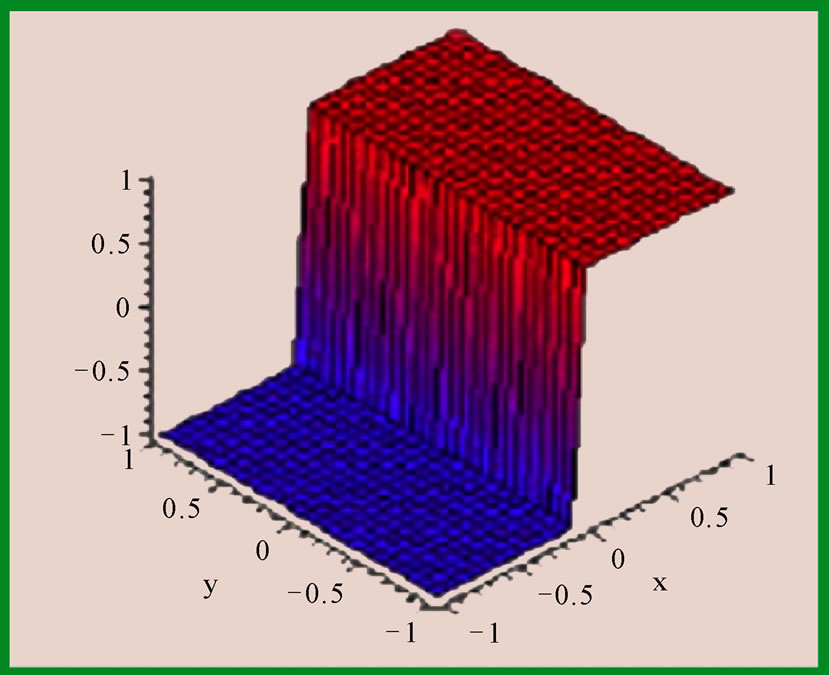
Figure 3. Heaviside jump function.
3.4. Numerical Integration
For the slit cut elements that are enriched with the jump function H(x), Moes [6] altered the routines quadrature element for the weak form assembly. Because the slit can be randomly directed in an element, the standard squaring of Gauss may not properly integrate the field of discontinuity. This process is generally carried out by means of dividing them into standard sub-triangles (Figure 4). Consequently whenever the slit propagates, a new subtriangles set and a new set of gauss points are used.
4. Method of the Level Set
The description of discontinuities in the context of the extended finite element method is often realized by the level-set method. The Method of level set is a numerical design of Osher [8] for interfaces movement modeling. The method is believed to represent an interface by the zero of a function, called the function of the level set, and the Hamilton-Jacobi’s equations modernized the function of the level set so as to know the interface speed in the normal direction to this interface (Figure 5).
A crack is described by two level sets (Figure 6):
• a normal level set, y(x), which the signed distance to the crack surface
• a tangent level set f(x), which is the signed distance to the plane including the crack front and perpendicular to the crack surface.
In a given element, ymin and ymax, respectively, be the minimum and maximum nodal values of y on the nodes of that element. Similarly, let fmin and fmax, respectively be the minimum and maximum nodal values of f on the nodes of an element:
• If f < 0 and ymin ymax £ 0, then the crack cuts through the element and the nodes of the element are to be enriched with H(x).
• If in that element fmin fmax £ 0 and ymin ymax £ 0, then the tip lies within that element, and its nodes are to be enriched Fi(r, q).
5. Programming Procedure
One can apply the method of finite extended element within one finite element code with relatively slight alterations: variable degrees numbers of freedom per node; interaction of mesh geometry (a manner to detect elements intersecting with discontinuity geometry); matrices of enriched rigidity; numerical integration. Sukumar and Prévost [9] described the X-FEM execution to model discontinuities of cracks within Dynaflow [10], as a package of standard finite element. Huang et al. [11] concentrated on the X-FEM application to problems of

Figure 4. Numerical integration schema.

Figure 5. Level set representation.
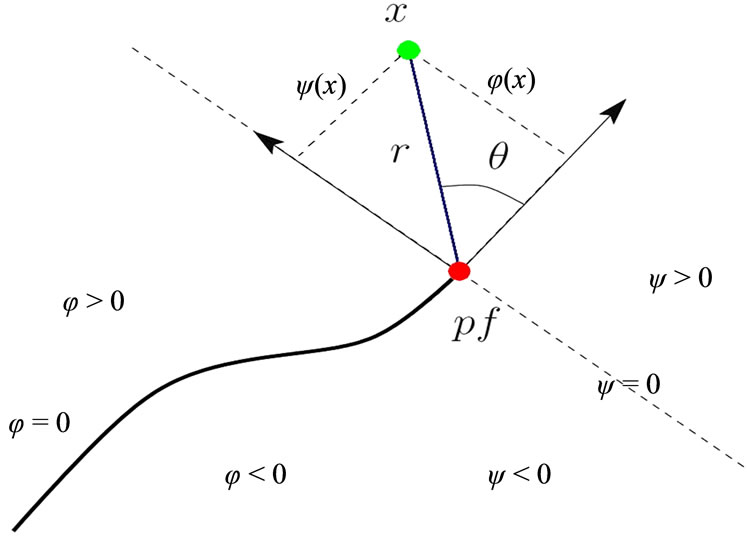
Figure 6. Coupling XFEM/LSM.
cracks in isotropic and bi-material media. Nisto et al.’s suggestion [12] of a numerical establishment in an explicit code was to treat the propagation of active cracks. The explicit dynamic FEM code (DynELA) [13] developed in the LGP with an object-directed framework to support the X-FEM application as a new module called DynaCrack. Bordas extended finite element library [14], the structure program, was conceived to fit all natural modularity, extensibility and robustness requirements. (C++) and of a commercial package of solid modeling/ finite element.
The XFEM method can be implemented within a finite element code with relatively small modifica-tions: variable number of degrees of freedom per node; mesh geometry interaction; enriched stiff-ness matrices; numerical integration [9].
1) Input data: defining various object entities (crack, holes, inclusions, interfaces…), enrichment types and crack growth law.
2) Nodal degrees of freedom: a part from the classical degrees of freedom, additional unknown enriched degrees of freedom is introduced via the displacement approximation.
3) Mesh-geometry interactions: This sub-category detects the selection of the enriched nodes, then touches upon the computation of enrichment functions, and detects the partitioning of the finite elements that are intersected by the crack.
4) Assembly procedure: The stiffness matrix and force vector assembly are done on an element level, which is similar to classical finite element implementation. The distinction herein is that the dimensions of the element stiffness matrix can differ from element (unenriched) to element enric-hed).
5) Post-processing: This sub-category addresses the main objectives of a fracture analysis by determining the interaction integral, and controlling the crack growth criteria.
The task of incorporating the X-FEM capabilities within a general-purpose finite element program can be broken down into the following schema (Figures 7 and 8, Table 1):
6. Numerical Experimentation
The Figures 9-12 show tow examples of crack growth modeling without re-meshing obtained by X-FEM code.
7. Conclusions
The extended finite element method (X-FEM) uses the partition of unity to remove the need to mesh physical surfaces or to remesh them as they evolve. It allows to model cracks, material inclusions and holes on non conforming meshes. The methodology of X-FEM that differs from that of the traditional method of finite element is of very particular concern since it does not force discontinuities to go with the borders. It solves the technological problems in the various complex fields accurately; the thing that can hardly be achieved impossible when using the traditional method of finite element alone. In this work, we present the basic concepts and the implantation of the X-FEM. The work discusses general algorithms for implementing an efficient X-FEM. A numerical experiment is provided to demonstrate the effectiveness

Figure 7. Structural scheme of the X-FEM code.
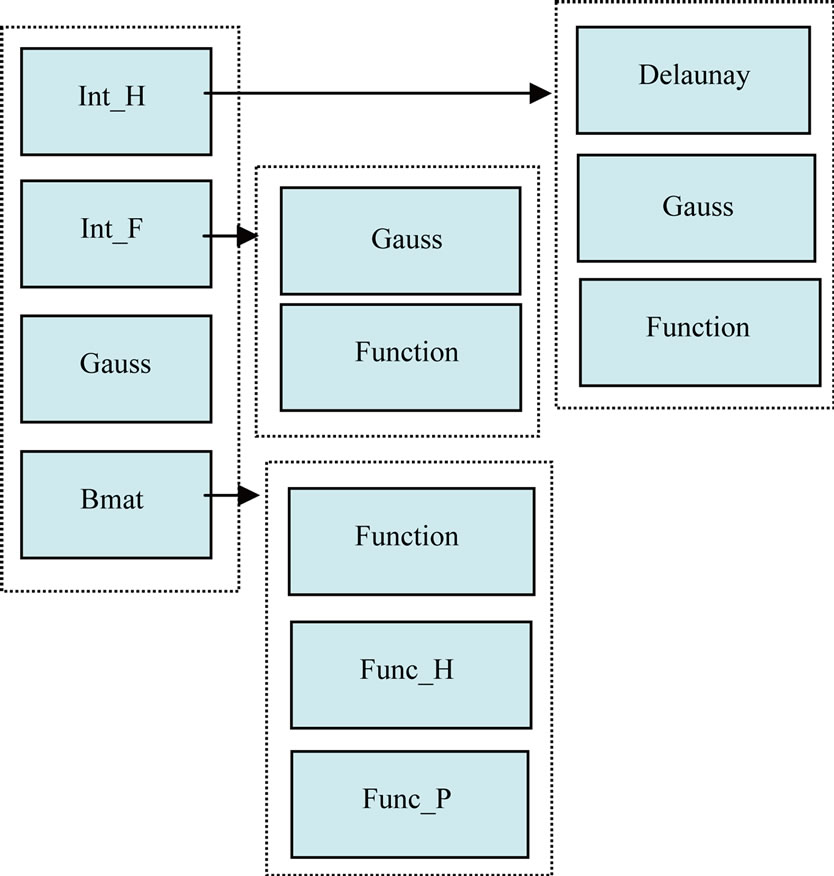
Figure 8. Structural scheme of Rigidity bloc.


Table 1. List of X-FEM functions.
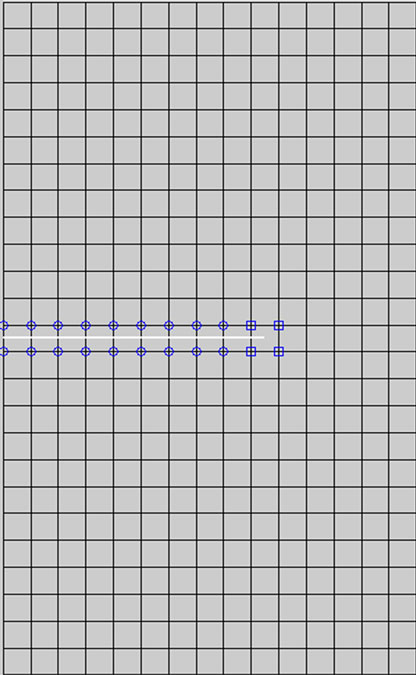
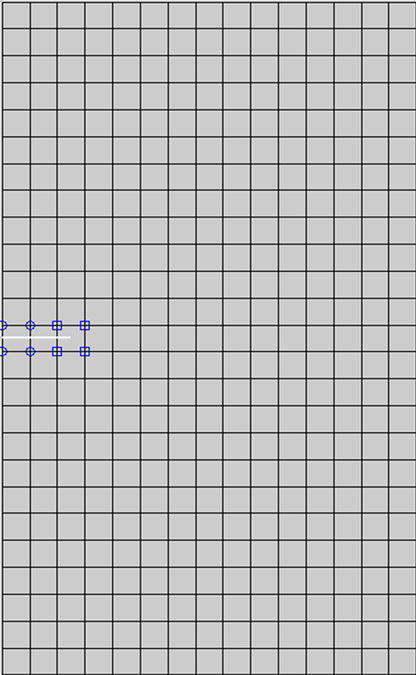
Figure 9. Crack growth modeling by X-FEM (SEN specimen).


Figure 10. Crack growth modeling by X-FEM (CN specimen).
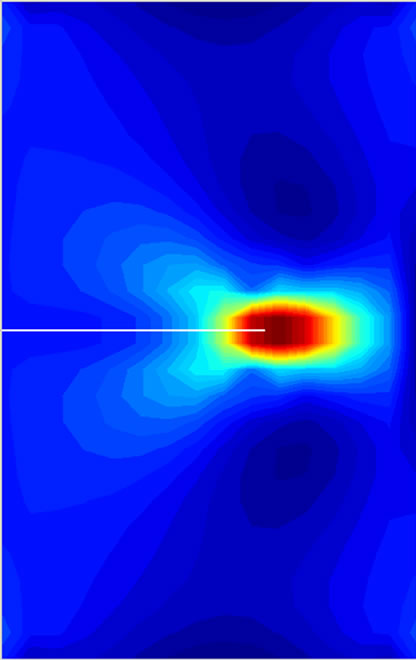

Figure 11. Stress distribution for different crack lengths (SEN specimen).
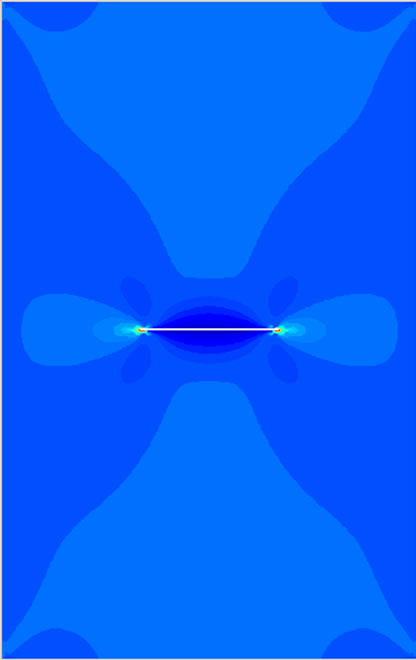

Figure 12. Stress distribution for different crack lengths (CN specimen).
and robustness of the X-FEM implementation.
8. REFERENCES
- P. Tong and T. Pian, “On the Convergence of the Finite Element Method for Problems with Singularity,” International Journal of Solids and Structures, Vol. 9, No. 3, 1973, pp. 313-321. doi:10.1016/0020-7683(73)90082-6
- T. Belytschko and T. Black, “Elastic Crack Growth in Finite Elements with Minimal Remeshing,” International Journal for Numerical Methods in Engineering, Vol. 45, No. 5, 1999, pp. 601-620. doi:10.1002/(SICI)1097-0207(19990620)45:5<601::AID-NME598>3.0.CO;2-S
- Y. Abdelaziz and A. Hamouine, “A Survey of the Extended Finite Element,” Computers and Structures, Vol. 86, No. 11-12, 2008, pp. 1141-1151. doi:10.1016/j.compstruc.2007.11.001
- Y. Abdelaziz, A. Nabbou and A. Hamouine, “A State- of-the-Art Review of the X-FEM for Computational Fracture Mechanics,” Applied Mathematical Modelling, Vol. 33, No. 12, 2009, pp. 4269-4282. doi:10.1016/j.apm.2009.02.010
- J. Dolbow, “An Extended Finite Element Method with Discontinuous Enrichment for Applied Mechanics,” PhD Thesis, Northwestern University, Chicago, 1999.
- N. Moes, J. Dolbow and T. Belytschko, “A Finite Element Method for Crack Growth without Remeshing,” International Journal for Numerical Methods in Engineering, Vol. 46, No. 1, 1999, pp. 131-150.
- M. Stolarska, D. D. Chopp, N. Moes and T. Belyschko, “Modelling Crack Growth by Level Sets in the Extended Finite Element Method,” International Journal for Numerical Methods in Engineering, Vol. 51, No. 8, 2001, pp. 943-960. doi:10.1002/nme.201
- S. Osher and J. Sethian, “Fronts Propagating with Curvature Dependent Speed: Algorithms Based on Hamilton-Jacobi Formulations,” Journal of Computational Physics, Vol. 79, No. 1, 1988, pp. 12-49. doi:10.1016/0021-9991(88)90002-2
- N. Sukumar and J. H. Prevost, “Modeling Quasi-Static Crack Growth with the Extended Finite Element Method Part I: Computer Implementation,” International Journal of Solids and Structures, Vol. 40, No. 26, 2003, pp. 7513- 7537. doi:10.1016/j.ijsolstr.2003.08.002
- J. Prevost, “Dynaflow,” Princeton University, Princeton, 1983.
- R. Huang, N. Sukumar and J. Prevost, “Modeling QuasiStatic Crack Growth with the Extended Finite Element Method Part II: Numerical Applications,” International Journal of Solids and Structures, Vol. 40, 2003, pp. 7539-7352. doi:10.1016/j.ijsolstr.2003.08.001
- I. Nistro, O. Pantale and S. Caperaa, “On the Modeling of the Dynamic Crack Propagation by Extended Finite Element Method: Numerical Implantation in DYNELA Code,” 8th International Conference on Computational Plasticity, Barcelona, 5-8 September 2005.
- O. Pantale, S. Caperaa and R. Rakotomalala, “Development of an Object Oriented Finite Element Program: Application to Metal Forming and Impact Simulation,” Journal of Computational and Applied Mathematics, Vol. 186, No. 1-2, 2004, pp. 341-351.
- S. Bordas, P. Nguyen, C. Dunant, H. Dang and A. Guidoum, “An Extended Finite Element Library,” International Journal for Numerical Methods in Engineering, Vol. 2, 2006, pp. 1-33.

