Intelligent Control and Automation
Vol.06 No.01(2015), Article ID:53319,9 pages
10.4236/ica.2015.61006
Dual Dynamic PTZ Tracking Using Cooperating Cameras
Mohammed A. Eslami, John R. Rzasa, Stuart D. Milner, Christopher C. Davis*
Department of Electrical and Computer Engineering, University of Maryland, College Park, USA
Email: meslami@umd.edu, rzasaman@umd.edu, *davis@umd.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 December 2014; accepted 4 January 2015; published 19 January 2015
ABSTRACT
This paper presents a real-time, dynamic system that uses high resolution gimbals and motorized lenses with position encoders on their zoom and focus elements to “recalibrate” the system as needed to track a target. Systems that initially calibrate for a mapping between pixels of a wide field of view (FOV) master camera and the pan-tilt (PT) settings of a steerable narrow FOV slave camera assume that the target is travelling on a plane. As the target travels through the FOV of the master camera, the slave cameras PT settings are then adjusted to keep the target centered within its FOV. In this paper, we describe a system we have developed that allows both cameras to move and extract the 3D coordinates of the target. This is done with only a single initial calibration between pairs of cameras and high-resolution pan-tilt-zoom (PTZ) platforms. Using the information from the PT settings of the PTZ platform as well as the precalibrated settings from a preset zoom lens, the 3D coordinates of the target are extracted and compared to those of a laser range finder and static-dynamic camera pair accuracies.
Keywords:
Surveillance, PTZ Cameras, Cooperating Cameras

1. Introduction
Investigating the use of cooperating camera systems for real-time, high definition video surveillance to detect and track anomalies over time and adjustable fields of view is moving us towards the development of an automated, smart surveillance system. The master-slave architecture for surveillance, in which a wide field-of-view camera scans a large area for an anomaly and controls a narrow field of view camera to focus in on a particular target is commonly used in surveillance setups to track an object [1] - [3] . The static camera solution [4] - [6] , or the master-slave system architecture with static master camera [6] [7] are well-researched problems, but is limited by the field of view of the master camera.
In particular, due to the computational complexity arising from object identification, having such systems operate in real-time is a hurdle within itself [1] [2] [8] . These setups often use background subtraction to detect a target within the FOV of the static camera and use a homography mapping between the pixels of the static camera to the pan/tilt (PT) settings of the slave camera to focus on the target. Look-up tables [3] and interpolation functions [9] - [11] are common tools used to navigate through the different settings to find the optimum setting for target tracking [6] . Essentially, a constraint is placed on the target such as the percentage of the image it must cover, or the centering of the target within the image at all times, or a combination of the two, and the intrinsic/ extrinsic parameters are varied to find the optimum setting that best satisfies these constraints.
This paper presents a dual-dynamic camera system that uses in-house designed, high-resolution gimbals [12] , and commercial-off-the-shelf (COTS) motorized lenses with position encoders on their zoom and focus elements to “recalibrate” the system as needed to track a target. The encoders on the lenses and gimbals of the master camera control the slave camera to zoom in and follow a target as well as extract its 3D coordinate relative to the position of the master camera. This system interpolates the homography matrix between pixels of the master camera and angles on the slave camera for different pan/tilts of the master camera. The master camera will keep a target in a specific region within the image and adjust its angle based on the trajectory of the target to force the target to stay within that region.
The homography mapping between the master and salve camera is updated anytime the master camera moves, so as to keep the control between the master-slave cameras continuous. The master camera turns off background subtraction every time it detects that it needs to move and reinitializes it after it has completed its movement. This system operates in real-time, and since the encoder settings are in absolute coordinates it can potentially be used to provide a 3D reconstruction of the trajectory of the target.
2. System Architecture
2.1. General Overview
The goal of this system is to use high definition, uncompressed video to resolve a target of length 5 m, such as a car, at ranges of 100 s of meters. This involves choosing appropriate hardware to be able to meet these requirements and the necessary control algorithms to allow the system to operate in real-time.
Mathematically, this situation can be modeled for a camera with w-pixel resolution in the horizontal direction imaging an object at a distance l from the camera with a FOV of qFOV:
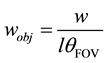 (1)
(1)
which provides an accuracy of 2 cm at a target range of 100 m and object size of 10 m (with the lens at maximum zoom, corresponding to a FFOV of 2) which should suffice in traffic surveillance applications.
2.2. Offline/One-Time Calibrations
To minimize the amount of image processing needed and thereby reduce the computational complexity of the problem, the processing needed for detecting the features to identify the target should be done only in one camera. These calibrations can be divided into two parts: 1) Computer vision algorithms and toolboxes to extract optical parameters and initialize the control algorithm, and 2) Generation and interpolation of the optical parameters extracted at various zoom settings for target localization. These two calibration parts are shown in Figure 1.
The Matlab toolbox [13] was used to extract the calibration parameters of the cameras and generate the look- up table (LUT) of the lens at the various zoom/focus settings, which were then interpolated in the same manner as [14] . The initial homography between the master camera’s pixels and the slave camera’s pan/tilt settings was found by corresponding nine pixel points in the master camera to nine pan/tilt settings of the slave camera. The pair of (x, y) coordinates retrieved from the master camera and (p, t) coordinates from the slave camera form a calibration point which obeys Equation (2), where H is a linear mapping (3 × 3 homography matrix) and s is a constant scale factor.
Figure 1. Calibration phase of the surveillance system.
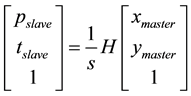 (2)
(2)
At selected zoom settings of each camera, singular value decomposition (SVD) is used to find the homography between the pixels of the master camera and the pan/tilt settings of the slave camera to bring the (x, y) calibration point to its center. Errors will arise from the fact that all lenses exhibit some shift in their optic axis [3] as they zoom in on a target.
This procedure is repeated for the various regions that are defined for the master camera. That is, the master camera is held to a particular pan/tilt setting that defines a region and one homography mapping is attributed to it. Then, the pan/tilt settings of the master camera are changed to define the next region and a new homography mapping is applied to the new region. Once all regions are defined, the elements of the various homography mappings are interpolated linearly to be able to control the slave camera with the appropriate homography mapping of the target in a specified region. Figure 2 shows the elements of the homography matrix for various pan/ tilt settings of a master/slave camera setup with a baseline of 1.5 m, focal lengths of 33 mm and 100 mm, respectively, for an area that is 70 × 70 m at a range of 150 m. The surface plot is a linear interpolation through the angles that were chosen for calibration. The reason for choosing a linear interpolation for the data will be explained in the description of the tracking phase of the system.
2.3. Real-Time Tracking
A large region of interest about the center defined in the master camera on every frame checks to ensure the target stays within its boundaries. The pan/tilt settings of the master camera are adjusted as the target moves above/below or to the left/right of this region of interest. The increment of adjustment used is the same as that of the linear calibration to ensure accuracy in the homography being used. Ideally, the master camera should not be moving too much since it has a wide field of view and thus using the linear interpolation between these schemes is satisfactory. Figure 3 shows the real-time tracking phase of the surveillance system.
Although the cameras are set in a master-slave relationship, the gimbal encoders from each camera are independent of one another. This amounts to having two independent, different viewpoints of the same scene, which provides stereovision. The range from such a setup can be approximated by a homogeneous linear method of triangulation, which often provides acceptable results. Its advantage over other methods is that it can be easily extended when additional cameras are added, a requirement of this system [15] .
3. Simulations and Experimental Results
3.1. Simulations
Simulations model a perfect world with no noise in choosing the pairs of pixel points and pan/tilt settings to calibrate the homography matrices between the master and slave. Essentially, points in the world are mapped to the image of the master camera via a projection matrix and rotation matrices are chosen for the slave camera to have that point fall in the center of its image. To achieve this, an initial guess can be derived for the slave camera to point at the world point by finding the vector C from Equation (3) and is shown in Figure 4.
Figure 2. Homography matrix elements for various pan/tilt settings of the master camera.
Figure 3. Real-time tracking of surveillance system.
Figure 4. Initial guess to find the slave camera angles from master camera and baseline.
 (3)
(3)
The vector A is the fixed orientation of the master camera, and the vector B is the baseline vector between the master and the slave cameras. The projection matrix of the slave camera is then optimized to bring that world point into a region of within 10 pixels of the center of the slave image. A maximum of five bounces is allowed if the camera begins to hover around the world point as it tries to bring it within the center of its image. The pair of (x, y) coordinates retrieved from the master camera and (p, t) coordinates from the slave camera form a calibration point and this is repeated nine times.
Once the calibration stage is complete and all of the homographies are found, a target world coordinate is imaged into the master camera and the control algorithm is simulated to control the slave camera and localize the target. The simulated results are compared to pre-coded target coordinates and this is shown in Figure 5.
The y-coordinate shows the worse localization error at 10% of a surveyed area that is 50 ´ 50 ´ 150 m (Z coordinate ´ x coordinate ´ Y coordinate) large. This localization was extracted assuming the target is exactly centered within the slave camera. Another simulation recalculated the average relative error if the there was some noise added to the system that would cause the control algorithm to fail to bring the target exactly to the center of the slave camera FOV. This simulation is shown in Figure 6. It can be seen that increasing the baseline between the master and slave cameras reduces the localization error.
Figure 5. Relative error in the coordinates for a random walk in the calibrated environment. The x-axis is the iteration number while the y-axis is the relative error in localizing the target using stereovision versus the known simulated coordinate.
Figure 6. Positioning error with additive noise at different baseline measurements. Larger baselines compensate for the error produced by the noise.
An advantage of this system is that it does not need to corresponding features between cameras since the homographies will all be precalibrated manually. So long as the target is found in a single camera, the second camera will follow the target, without the need for image segmentation and identification algorithms.
3.2. Experimental Results
The experimental setup consisted of two Fujinon C22X23R2D-ZP1 motorized zoom lenses with digital preset to ensure that the precise position of the zoom and focus elements were known. The lenses were equipped with 16- bit encoders to accurately calibrate for the focal length by using the MATLAB camera calibration toolbox [13] at a number of zoom settings fitting the model to the commonly used exponential model between zoom/focus settings and focal length. The plots retrieved are similar to those shown by Wilson [14] and other surveillance papers that have motorized zoom capabilities [1] [2] . The cameras used in the stereo setup are Allied Vision Technologies GC1600CH, 2-Megapixel, 25 fps, Gigabit Ethernet machine vision cameras streaming uncompressed video data. The gimbals used are designed in-house [12] with a common yolk-style platform giving 360˚ continuous pan range and ±40˚ tilt range. The gimbals are driven with two direct-drive brushless AC servo motors with 20bit absolute encoders giving 0.000343˚ readout resolution. They are equipped to hold 50 lbs and have a 0.002˚ positioning repeatability with the optical system used in this work. The full system is shown in Figure 7. There were two experiments that were conducted: 1) Target localization and 2) Real-time surveillance tracking.
Figure 8 and Figure 9 show experimental results obtained from the ranging experiment with the hardware setup. The Biomolecular Services Building across from the Kim Engineering Building on the Universtiy of Maryland campus was used as the plane for calibration, and points were selected in the tracking phase to center the slave camera. Google Earth was used to find the distance of the building relative to our laboratory and these were compared to the results given from the camera system. Google Earth’s numbers were also confirmed with a GLR225 Bosch laser range finder by giving a measured distance between the buildings on the order of 170 m. The (X, Y) positions are roughly estimated based on the size of the windows on the building, which are 1.2 m wide by 1.3 m high.
The surveillance setup was housed in the Kim Engineering building to track a single target in the parking lot, which was divided up into four regions. A failure of surveillance occurs anytime the target moves out of the field of view of the slave camera [16] . Testing the surveillance setup in real-time (12 fps) at 405 × 305 resolution to track a target also showed excellent alignment capabilities as seen in Figure 10. A false positive in the experiment is defined as a feature that is detected which is not the target. They are a result of the master camera adjusting its setting to bring the target back within its region of interest. An average of two false positives were detected in 10 different adjustments of the master camera. These false positives can be minimized and/or eliminated by increasing the number of learning images needed to detect a background so that new objects within the scene are not considered as moving foreground objects. Increasing the number of images to find a background, however, does increase the latency in tracking the target with the slave camera.
Figure 7. Master-slave camera surveillance setup (refer to gimbals gra- phically like master and slave).
Figure 8. (a) Master Camera looking at a building with its point selected shown in red; (b) Slave camera centering that point within its image and computing the position relative to the master camera.
Figure 8. (a) Master Camera looking at a building with its point selected shown in red; (b) Slave camera centering that point within its image and computing the position relative to the master camera.
4. Conclusions/Future Work
We designed and developed a novel system with multiple dynamic cameras to track a target’s 3D coordinate relative to the master camera in a master-slave relationship. As the target moved out of the region of interest in the master camera, the master camera moved to bring the target back into a certain predefined window. Calibrations between pan/tilt settings of the slave camera and pixel settings of the master camera are then updated based on the moves of the master camera to ensure the slave camera keeps the target within its center. The absolute encoders available on the optical system and the gimbals were then used in a stereo setup to find the 3D coordinate of the target relative to the master camera in real-time. To improve ranging accuracies, it was shown through simulation that the baseline of the system should be increased. This is relatively easy to incorporate within the master-slave system described.
To expand on the system currently running in real-time in our laboratory would require an implementation of
Figure 9. (a) Master Camera looking at a building with its point selected in a box; (b) Slave camera centering that point within its image and computing the position relative to the master camera.
Figure 9. (a) Master Camera looking at a building with its point selected in a box; (b) Slave camera centering that point within its image and computing the position relative to the master camera.
image features to be used for correspondence. These vision algorithms are computationally expensive if they are to be run on the whole image, particularly when the video stream is in the form of uncompressed megapixel imagery data coming from machine vision cameras. Therefore, the master-slave relationship can act as an initialization of a region to correspond features. The larger baselines on the order of 7 m and above could then be tested to monitor the improvements of correspondence between the respective video streams. If the baseline is too large, the lighting coming into one camera could show a completely different image of the same scene between the two cameras and correspondence would fail. The initialization of two regions that should correspond to one another will help to alleviate this problem.
Our system was implemented with two cameras and a single target. A next step would be to use this setup as a single node within a much larger surveillance network. The network would communicate through a secondary control network to pass a target ID, namely the measured 3D coordinate and velocities from optic flow measurements, to other nodes for a longer track period. A lower data rate secondary channel would communicate small portions of data would allow the network to hand off the target from node to node in real-time. This would be a step towards the development of a fully cooperating, smart surveillance system.


Figure 10. Surveillance system after calibration tracking a target moving from (a) Region 1; to (b) Region 2; (c) Region 3.
Support
This work was supported by the U.S. Department of Transportation and the Federal Highway Administration Exploratory Advanced Research Program contract. (DTFH6112C00015).
References
- Zhou, J. and Wan, D. (2008) Stereo Vision Using Two PTZ Cameras. Computer Vision and Image Understanding, 112, 184-194. http://dx.doi.org/10.1016/j.cviu.2008.02.005
- Zhou, J., Wan, D. and Ying, W. (2010) The Chameleon Like Vision System. IEEE Signal Processing Magazine, 27, 91-101. http://dx.doi.org/10.1109/MSP.2010.937310
- Badri, J., Tilmant, C., Lavest, J.-M. and Pham, Q.-C. (2007) Camera-to-Camera Mapping for Hybrid Pan-Tilt-Zoom Sensors Calibration. Lecture Notes in Computer Science, 4522, 132-141.
- Horaud, R., Knossow, D. and Michaelis, M. (2006) Camera Cooperation for Achieving Visual Attention. Machine Vision Applications, 16, 331-342. http://dx.doi.org/10.1007/s00138-005-0182-9
- Khan, S., Javid, O. and Rasheed, Z. (2001) Human Tracking in Multiple Cameras. Proceedings of IEEE International Conference of Computer Vision, 331-336.
- Senior, A., Hampapur, A. and Lu, M. (2005) Acquiring Multi-Scale Images by Pan-Tilt-Zoom Ontrola nd Automatic Multi-Camera Calibration. IEEE Workshop on Applications on Computer Vision, 433-438.
- Sinha, S. and Pollefeys, M. (2004) Towards Calibrating a Pan-Tilt-Zoom Camera Network. EECV Conference Workshop.
- Nelson, E.D. and Cockburn, J.C. (2007) Dual Camera Zoom Control: A Study of Zoom Tracking Stability. Proceedings of IEEE International Conference of Acoustics, Speech and Signal Processing, 941-944.
- Bazin, J.-C. and Demonceaux, C. (2008) UAV Attitude Estimation by Vanishing Points in Catadioptric Images. International Conference on Robotics and Automation, 2743-2749.
- Caprile, B. and Torre, V. (1990) Using Vanishing Points for Camera Calibration. International Journal of Computer Vision, 4, 127-140. http://dx.doi.org/10.1007/BF00127813
- Chen, Y.S., Hung, Y.P., Fuh, C.S. and Shih, S.W. (2000) Camera Calibration with a Motorized Zoom Lens. International Conference on Pattern Recognition, 495-498.
- Rzasa, J., Milner, S.D. and Davis, C.C. (2011) Design and Implementation of Pan-Tilt FSO Transceiver Gimbals for Real-Time Compensation of Platform Distrubances Using a Secondary Control Network. SPIE Laser Communication and Propagation through the Atmosphere and Oceans, San Diego.
- Bouget, J. http://www.vision.caltech.edu/bouguetj/calib_doc/
- Wilson, R.K. (1994) Modeling and Calibration of Automated Zoom Lenses. Proceedings of SPIE, 170-186.
- Hartley, R. and Zisserman, A. (2003) Multiple View Geometry in Computer Vision. 2nd Edition, Cambridge University Press, Cambridge.
- Chen, C.-H., et al. (2008) Heterogeneous Fusion of Omnidirectional and PTZ Cameras for Multiple Object Tracking. IEEE Transactions on Circuits and Systems for Video Technology, 18, 1052-1063. http://dx.doi.org/10.1109/TCSVT.2008.928223
NOTES
*Corresponding author.











