Intelligent Control and Automation
Vol. 4 No. 3 (2013) , Article ID: 35561 , 8 pages DOI:10.4236/ica.2013.43034
Robust Adaptive Neural Network Control for XY Table
1Department of Intelligent System Engineering, Graduate School of Dong-eui University, Busan, South Korea
2Department of Mechatronics Engineering, Dong-eui University, Busan, South Korea
Email: **************
Copyright © 2013 Nguyen Hoang Giap et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 21, 2013; revised June 21, 2013; accepted July 1, 2013
Keywords: Robust Adaptive Neural Network; Motion Control; XY Table; DSP
ABSTRACT
This paper proposed a robust adaptive neural network control for an XY table. The XY table composes of two AC servo drives controlled independently. The neural network with radial basis function is employed for velocity and position tracking control of AC servo drives to improve the system’s dynamic performance and precision. A robust adaptive term is applied to overcome the external disturbances. The stability and the convergence of the system are proved by Lyapunov theory. The proposed controller is implemented in a DSP-based motion board. The validity and robustness of the controller are verified through experimental results.
1. Introduction
The XY tables have taken an important role in manufacturing systems. Generally, the XY table is a ball-screw driven mechanism actuated by two AC servo drives. Such mechanism often exist many kinds of disturbances, nonlinear friction and uncertainties that limit the tracking performance of controlled system. In order to improve the performance of XY table, many works have been presented [1-3]. In [4], a combination of friction-modelbased feed-forward and inverse-model-based disturbance observe is used to reduce the radial tracking error and quadrant glitches of linear-drive XY table. This technique increases the system bandwidth, hence improves the overall tracking performance. However, robustness to variations of system parameters and uncertainties among each axis mechanism were not considered in the design of the compensation.
In most manufacturing processes, XY table often utilizes two AC servo motors and couples their output shafts to mechanical translators such as gears or bears to perform linear motions. Such mechanical systems have been extensively used in the industrial market due to low cost, high torque density, little torque ripple and power saving. Along with their intensive applications, many works have been conducted to enhance the performance of the motion control system [5-7]. In [8], the authors developed an auto-disturbance rejection controller based on a nonlinear tracking-differentiator, an extended states observer and a nonlinear PD control to achieve high performance and large robustness motion control. Although this simple method can archive high precision of AC servo system under unknown parameters and large load disturbance, the stability of the whole system is not guaranteed. In [9], a back propagation neural network is used to identify the dynamic parameters of AC servo motor. Although the controller obtained excellent performance compared with traditional PID controller, the load torque disturbance and uncertainties were not considered in the design.
In this paper, we propose a robust adaptive neural network (RANN) scheme to overcome such described drawbacks. The main aim of our controller is to define an augment error related to the angular position error and angular velocity error. Then the controller is designed so that the augment error can converge toward zero asymptotically. This process makes the angular velocity error and angular position error stable asymptotically. The controller is able to guarantee the convergence and stability of the servo system despite the existence of model uncertainties and external disturbances. In this controller, a 2-layer neural network with radial basis function is used to approximate the nonlinear factors of the AC servo motor. A robust adaptive control scheme is applied to suppress the disturbances and guarantee the stability of the system. The proposed robust adaptive neural network controller is implemented in a motion controller based on the high performance digital signal processor (DSP) TMS320C6727. The high speed DSP allows the closedloop controller and reference trajectory generators to be implemented in the DSP, while the feedback position signals with digital filter and digital inputs/outputs are carried out in the FPGA to reduce the computational load of DSP. Afterward, the output current control is put forward to the analog amplifier to drive the motor. This hardware structure allows for designing a highly sampled, flexible and compact motion controller.
This paper is organized as follows. Section 2 describes the development of robust adaptive neural network controller with the proof of asymptotic stability. Section 3 presents experimental results, including the comparison of the traditional PID controller and the proposed controller. Section 4 draws the conclusions.
2. Development of Robust Adaptive Neural Network Controller
2.1. Model of Two-Axis XY Table
The XY table used in this paper is composed of two AC servo drives controlled separately. Therefore, dynamic equation of a single-axis AC servo drive can be described in a rotating reference frame as following:
 (1)
(1)
where ![]() is angular velocity of the rotor, J is the moment of inertia,
is angular velocity of the rotor, J is the moment of inertia, 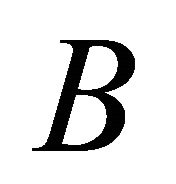 is the viscous coefficient.
is the viscous coefficient. ![]() is the driving torque,
is the driving torque, 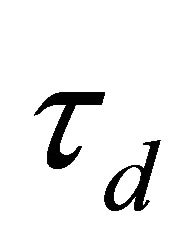 can be considered as the unknown load torque disturbance on the rotating shaft.
can be considered as the unknown load torque disturbance on the rotating shaft.
In the system design, it is assumed that the reference angular position is a continuous and differentiable signal. Therefore, the angular velocity and angular acceleration can be expressed as:
 (2)
(2)
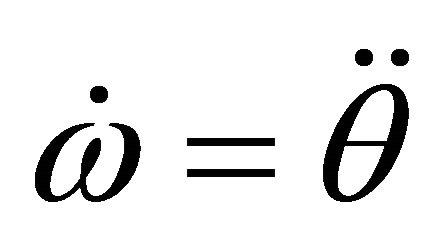 (3)
(3)
where  is the angular position.
is the angular position.
The goal of our control scheme is to achieve asymptotic tracking for a given continuous reference trajectory.
2.2. Introduction of Feed-Forward Neural Network with Radial Basis Function
Two-layer feed-forward neural network as shown in Figure 1 can be presented in matrix form:
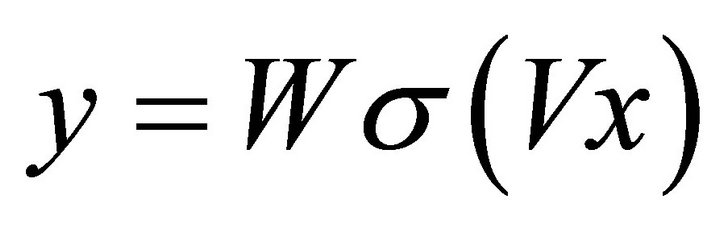 (4)
(4)
where 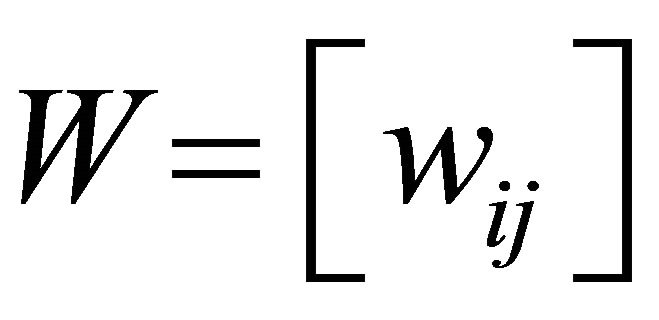 and
and 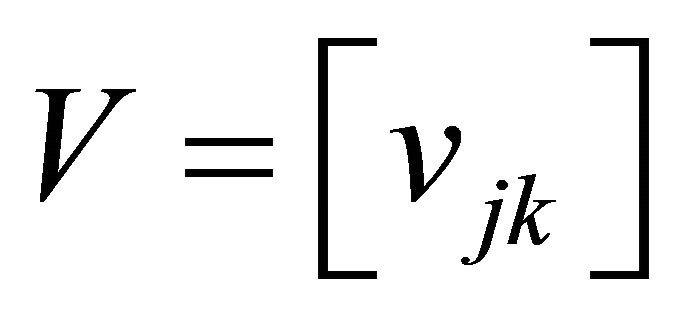 are the weight vectors,
are the weight vectors,
 is the input vector,
is the input vector,
 is the output vector, and
is the output vector, and
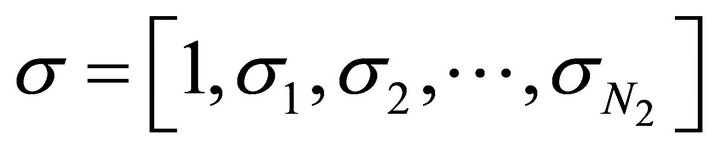 denotes the activation function vector. Constant 1 included in the vector
denotes the activation function vector. Constant 1 included in the vector ![]() and
and ![]() as a first term allows one to incorporate the thresholds
as a first term allows one to incorporate the thresholds 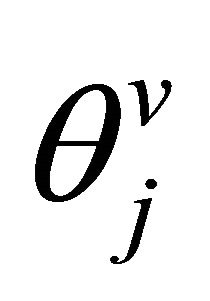

Figure 1. Two-layer feed-forward neural network.
and 
The well-known universal approximation property of a neural network proposed by Hornik et al. [10] says that for a nonlinear function , there exists a sufficiently large N2 number of neurons satisfying
, there exists a sufficiently large N2 number of neurons satisfying
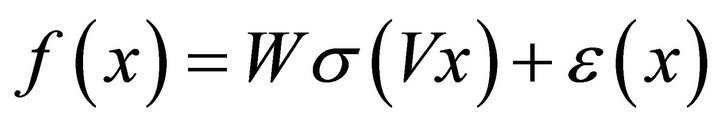 (5)
(5)
and makes the two-layer neural network functional approximation error vector  arbitrarily small.
arbitrarily small.
We know that the main disadvantage of the multilayer neural network is highly nonlinear in parameter. Hence, we consider hereafter the neural network of fixed V, which makes the neural network linearly parameterized. Defining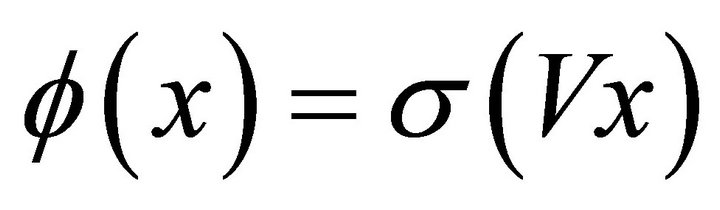 , we have
, we have
 (6)
(6)
where 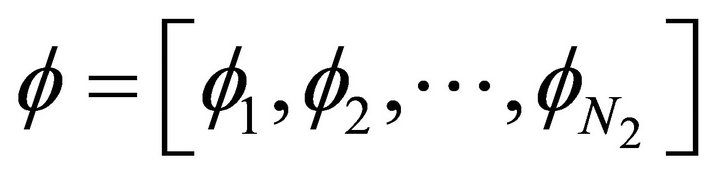 is the generalized basis function vector. In this paper, we use the radial basis function with Gaussian form as following:
is the generalized basis function vector. In this paper, we use the radial basis function with Gaussian form as following:
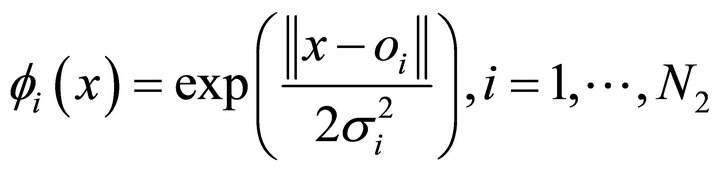 (7)
(7)
where ![]() is the center of the i-th radial basis function, and
is the center of the i-th radial basis function, and 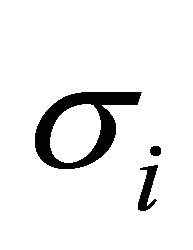 is the width coefficient.
is the width coefficient.
2.3. Controller Design
In this section, we introduce the design of proposed controller for AC motor based on the Lyapunov’s stability theorem. The strategy is to define an augment error and design a neural network with learning rules and a robust adaptive term to force the augment error to converge to zero asymptotically in spite of the presence of the system uncertainties and load torque disturbances.
The controller scheme is shown in Figure 2.
The angular position tracking error is denoted as:
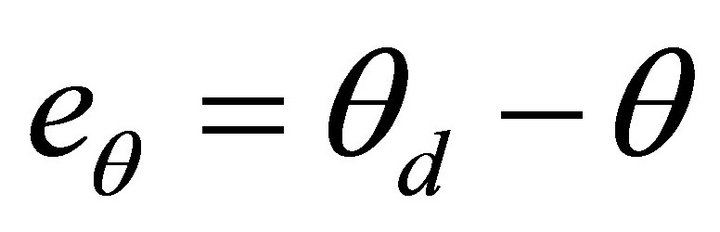 (8)
(8)

Figure 2. Controller scheme.
where 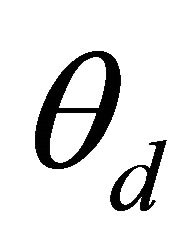 is the desired angular position.
is the desired angular position.
Differentiating Equation (8) with respect to time to get the angular position tracking error:
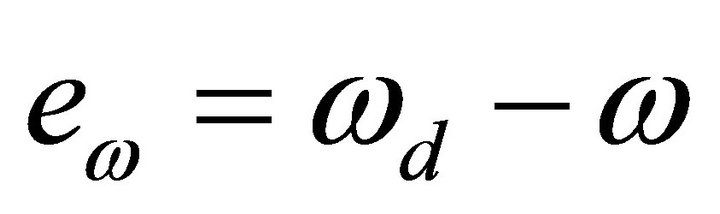 (9)
(9)
The angular velocity tracking error is presented as following:
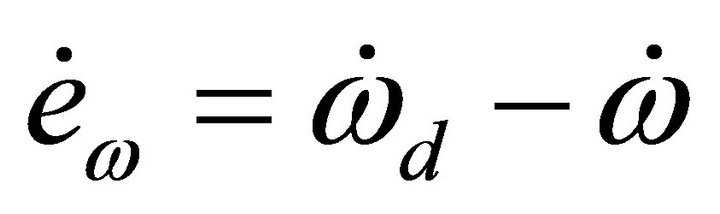 (10)
(10)
In order to solve the position tracking problem with asymptotical stability, we define the augment error as below:
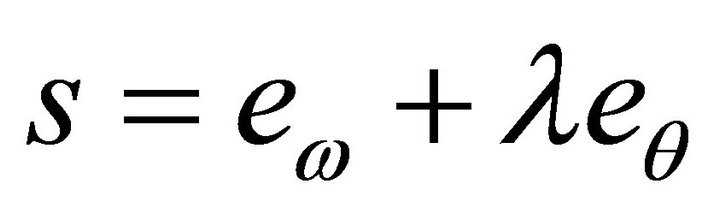 (11)
(11)
Differentiating Equation (11) and substituting it into dynamic Equation (1), we have the error dynamic equation:
 (12)
(12)
The nonlinear function containing the dynamic parameters of AC servo motor is defined as:
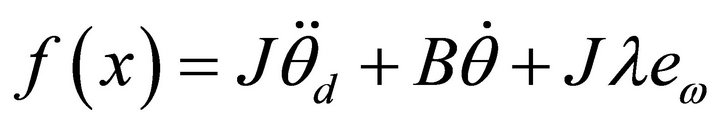 (13)
(13)
It is well-known that the neural network is capable of approximating any nonlinear function over compact input space [10]. The strategy is to construct a simple neural network with radial basis function as presented in Section II.B to approximate the nonlinear function (4). Therefore, the output of neural network controller can be rewritten as:
 (14)
(14)
Assumption 1: There exist unknown positive constants 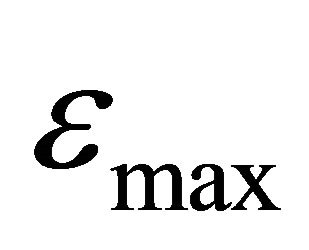 and
and 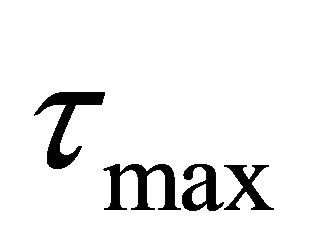 such that
such that 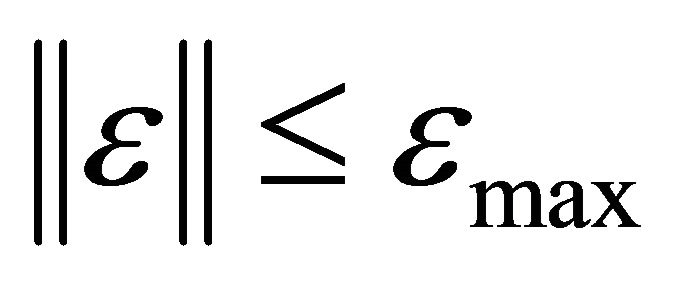 and
and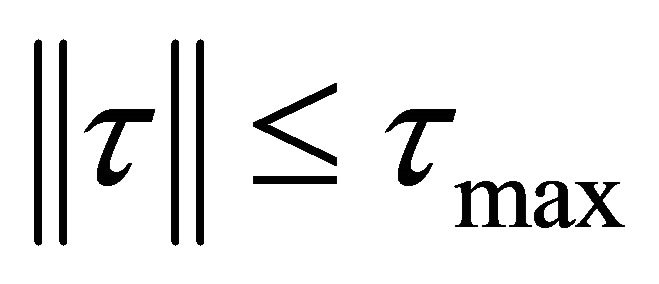 .
.
The torque control input is defined as:
 (15)
(15)
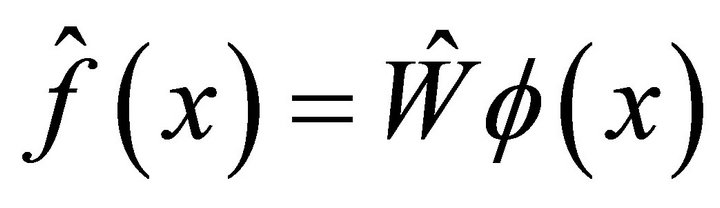 (16)
(16)
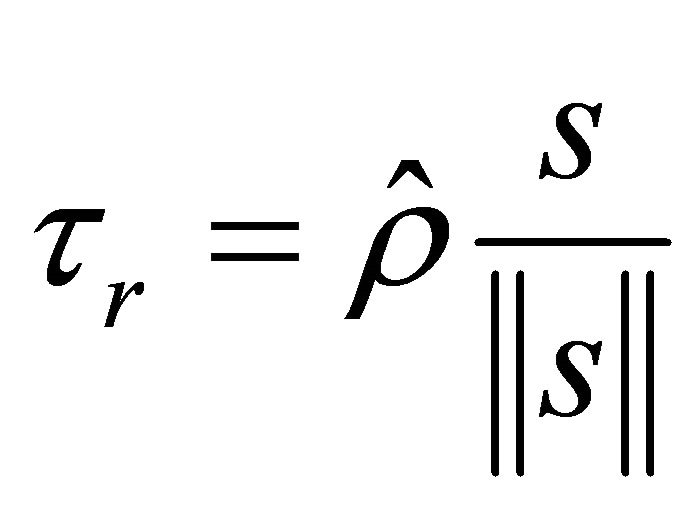 (17)
(17)
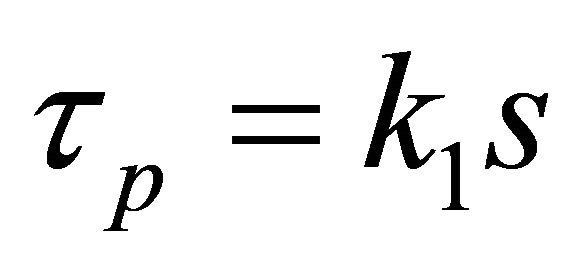 (18)
(18)
where 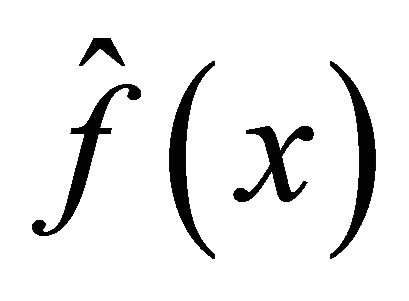 is the estimate function of the nonlinear function
is the estimate function of the nonlinear function ,
,  is estimate weight vector of
is estimate weight vector of ,
, 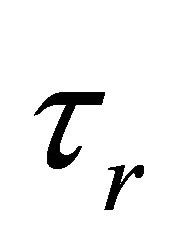 is the robust adaptive control input,
is the robust adaptive control input,  is the stabilizing control term, and
is the stabilizing control term, and  is a constant denoted as the rate of error convergence.
is a constant denoted as the rate of error convergence.
Substituting Equations (14) and (15) into Equation (12), we obtain the closed-loop error dynamics for augment error s:
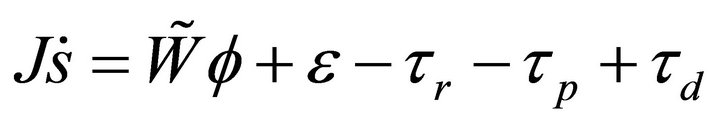 (19)
(19)
where  is the estimate weight error.
is the estimate weight error.
Consider the Lyapunov function:
 (20)
(20)
Differentiating Equation (20) with respect to time and substituting Equation (19) into the result, we can obtain:
 (21)
(21)
By choosing the weight update rule:
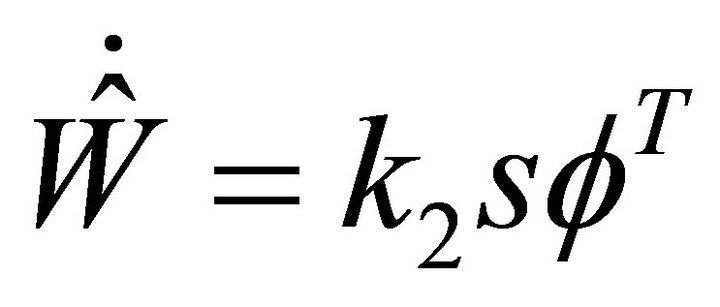 (22)
(22)
and combining with Assumption 1, we can infer the boundedness of Equation (21) as following:
 (23)
(23)
where 
Since 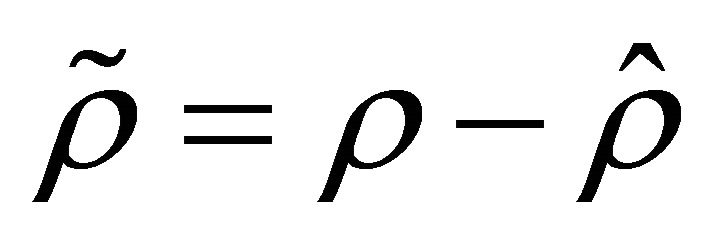 then
then
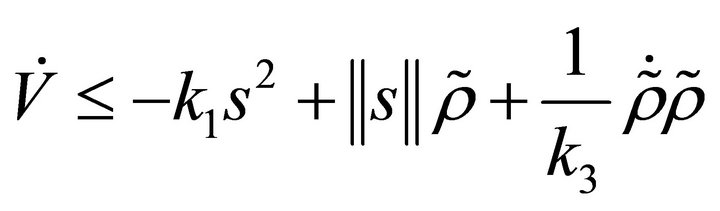 (24)
(24)
The adaptation rule is simply selected as:
 (25)
(25)
It can be seen that the adaptation law (25) suppresses the approximation estimation error and disturbance, allows the augment error to converge to zero asymptotically:
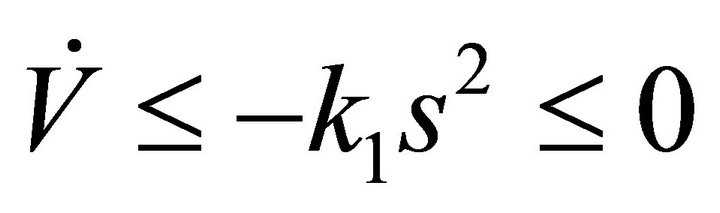 (26)
(26)
Because 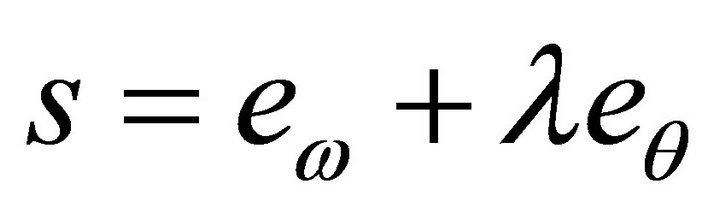 is dynamics stability,
is dynamics stability, 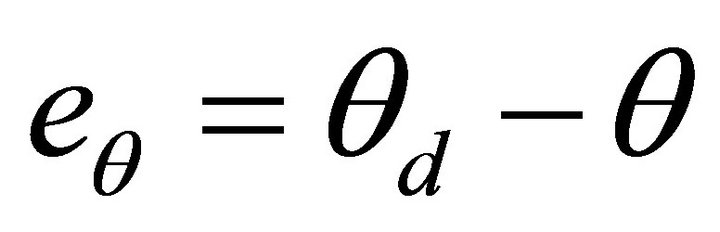 and
and 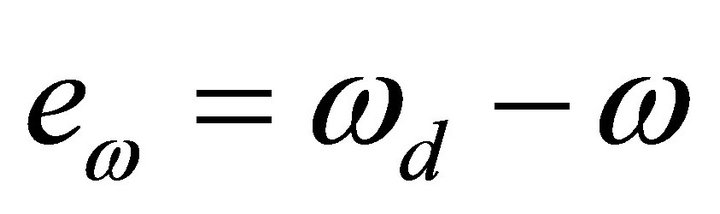 are asymptotically stable.
are asymptotically stable.
3. Experimental Results
The proposed motion control board as shown in Figure 3 is developed based on high performance floating point DSP TMS320C6727 with the CPU clock rate of 350 MHz. Moreover, the proposed controller includes multichannels of 16-bit DAC, DIO, encoder interface, and PCI interface. The servo interface, including encoder module, DAC control module, and DIO are designed in the FPGA XC3S1000. The PCI interface is built in the FPGA to communicate with the host PC. The DSP communicates with the PCI interface through Wishbone Connection Matrix structure. The block diagram of the proposed control board is shown in Figure 4.

Figure 3. Developed DSP-based motion controller.

Figure 4. Block diagram of DSP controller.
Code Composer Studio software is used to implement the algorithm in TMS320C6727. The overall algorithm is divided into two main parts: main module and runtime module. The main module defines and initializes the software variables, constants and specific registers. Moreover, some look-up tables employed in the algorithm is also addressed in this parts. Initialized registers in the initialization module are Phase-Locked-Loop (PLL) registers, timer registers, EDMA registers, EMIF registers, interrupt registers, and communication registers. The initialization module is called once at the beginning of the program. Runtime module is generated in the form of functional modules. This modularity technique is preferred to debug and maintain the code in an easy way. In motion control applications, the runtime module including overall control algorithms, trajectory generation, realtime updating of position and velocity variable, and digital filters is carried out by each interrupt clock.
The neural network structure using in the experiment has 3 inputs, 5 neurons in hidden layer, and 1 output layer. The initial weights and thresholds are set as 0.01. The weights vector is updated online by the learning rule proposed in Equation (16).
From the proof of stability, it can be seen that the constant  determines the convergence speed of augment error s. However, the bigger
determines the convergence speed of augment error s. However, the bigger  is, the higher torque is needed to drive the system.
is, the higher torque is needed to drive the system. 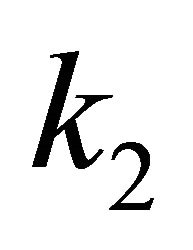 determines the learning speed of the neural network. Therefore, high gain
determines the learning speed of the neural network. Therefore, high gain  can avoid the system uncertainties.
can avoid the system uncertainties. 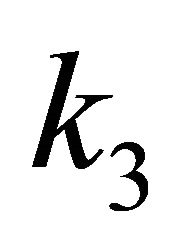 decides the adaptive speed of the robust term. Due to the characteristic of dynamics stability of augment error s, the constant λ should be chosen sufficiently small to guarantee the convergence of angular position error. In the simulation, the initial control gains and neural network structure are selected as:
decides the adaptive speed of the robust term. Due to the characteristic of dynamics stability of augment error s, the constant λ should be chosen sufficiently small to guarantee the convergence of angular position error. In the simulation, the initial control gains and neural network structure are selected as: ,
, 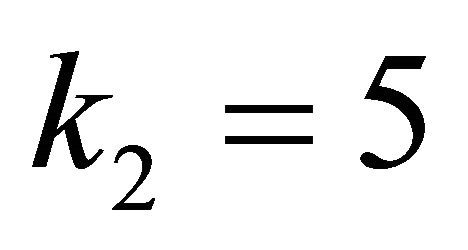 ,
, 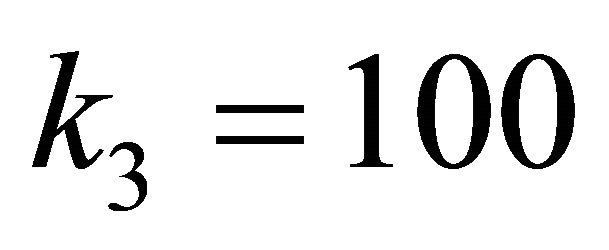 ,
,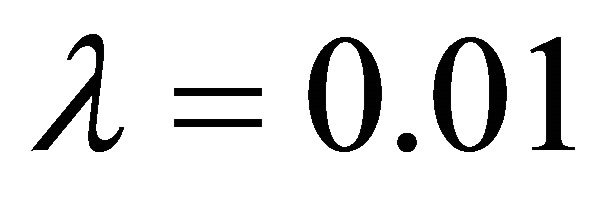 .
.
The overall experimental system setup shown in Figure 5 consists of a DSP-based motion controller, an ELMO analog amplifier, a LG FMA-CN02 servo motor with 2000 pulses/revolution feedback encoder, a linear stage RoboStar with 10 mm lead screw, and a host computer.
A circle path with center position 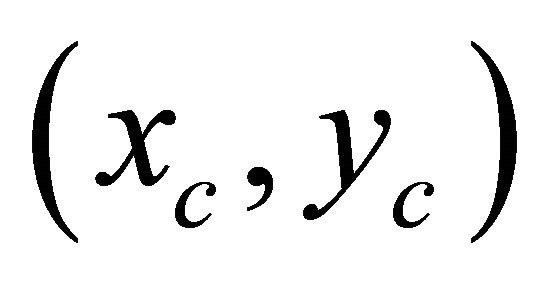 and radius R is designed as reference trajectory for the experiment, which can be presented by individual axes as following:
and radius R is designed as reference trajectory for the experiment, which can be presented by individual axes as following:
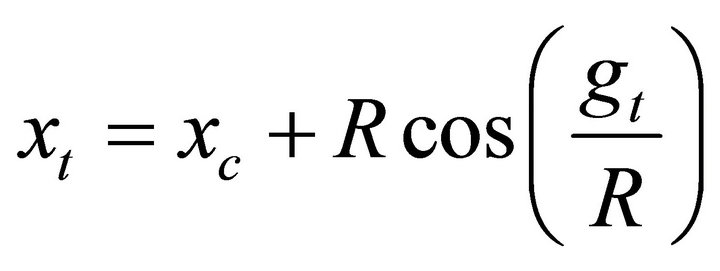 (27)
(27)
 (28)
(28)
The experimental results using conventional PID controller with the control gains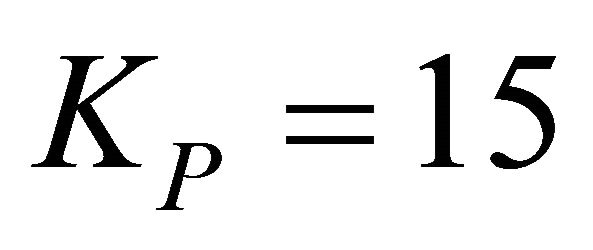 ,
, 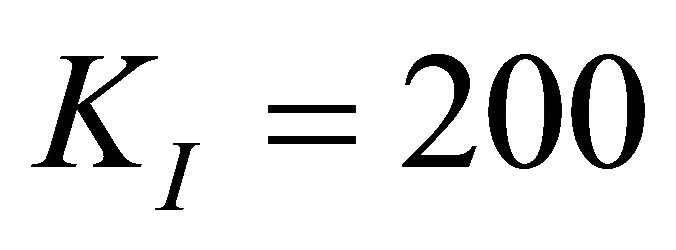 , KD = 0.15 are shown in Figures 6-12. Figure 13 shows the circular interpolation tracking of XY table. Figures 7
, KD = 0.15 are shown in Figures 6-12. Figure 13 shows the circular interpolation tracking of XY table. Figures 7
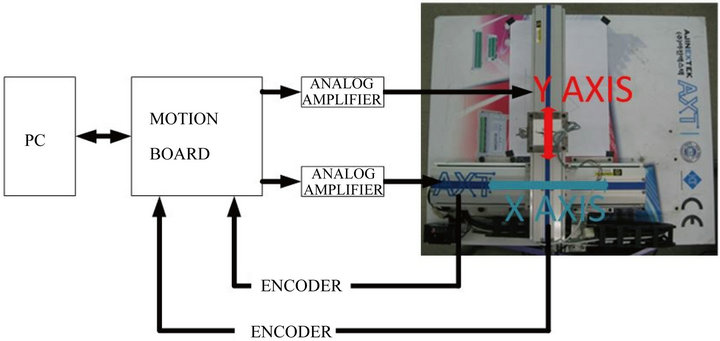
Figure 5. The proposed XY table motion control system.
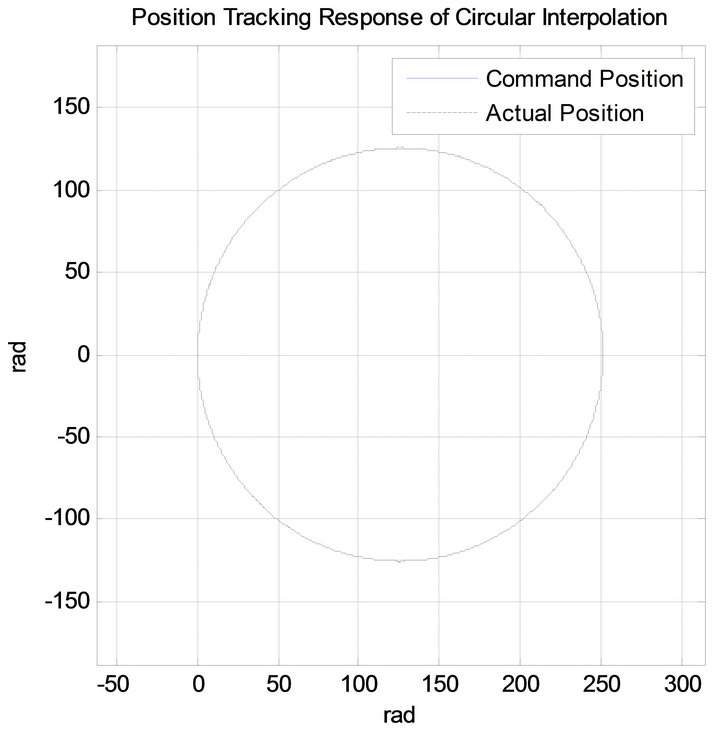
Figure 6. Position tracking response of circular interpolation using PID controller.
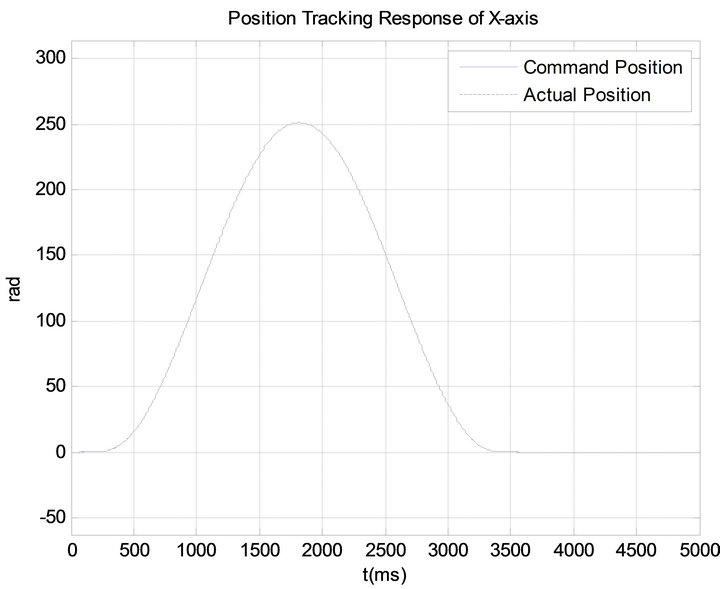
Figure 7. Position tracking response of X-axis using PID controller.

Figure 8. Position tracking error of X-axis using PID controller.

Figure 9. Control input of X-axis using PID controller.

Figure 10. Position tracking response of Y-axis using PID controller.
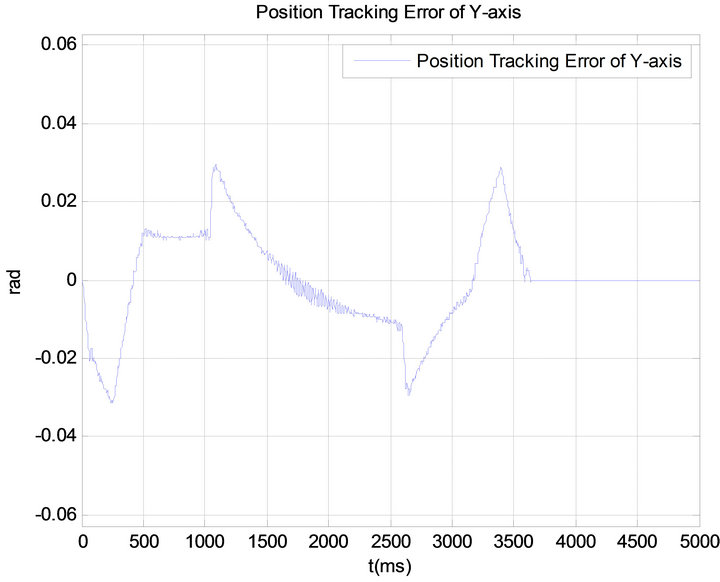
Figure 11. Position tracking error of Y-axis using PID controller.

Figure 12. Control input of Y-axis using PID controller.
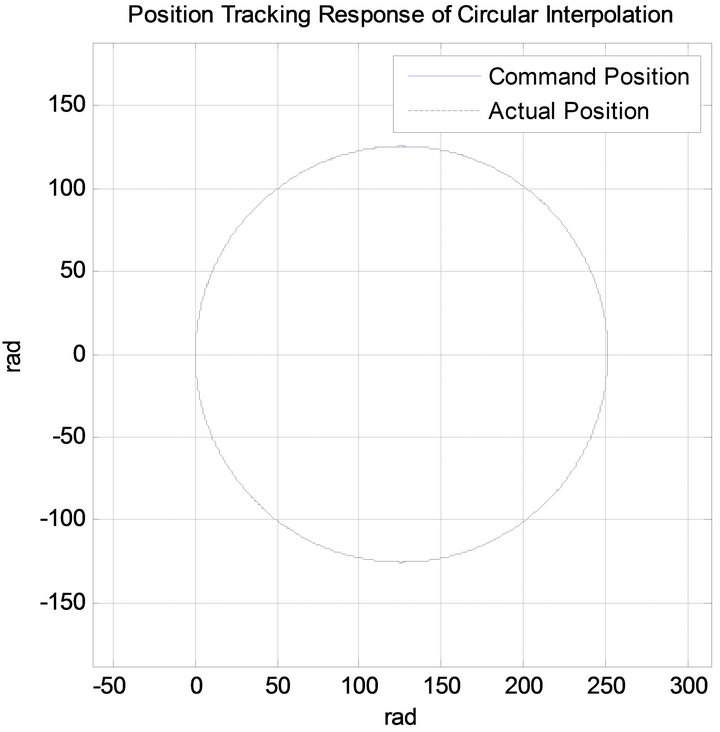
Figure 13. Position tracking response of circular interpolation using RANN controller.
and 10 are the trajectories of individual axis. Figures 9 and 12 present the input torque command of the PID controller. The tracing error of X-axis and Y-axis in Figures 8 and 11 show that during the motion path, PID controller is not able to reduce the tracking error since it is a linear feedback control system.
Figures 13-19 show the experimental results using proposed RANN controller. The convergence rate , the neural network learning rate
, the neural network learning rate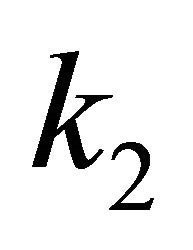 , the adaptive speed
, the adaptive speed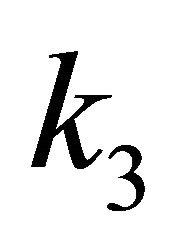 , and the constant
, and the constant ![]() are selected as 120, 0.0005, 100, and 0.01 respectively. The initial weights and thresholds in neural network are set as 0.01. It is clear from the experimental results that the tracking error is substantially reduced to nearly zero. The actual positions of the motors closely track the reference and tracking error converges to zero quickly. Moreover, the control input responses of X-axis and Y-axis shown in Figures 16 and 19 indicate the improvement of control effort of proposed controller, since it keeps the tracking error negligible during the motion path. On the contrary, the PID controller cannot produce sufficient torque command to keep tracking error of motor arbitrary small. Table 1 shows the comparison of the dynamic performance of the PID controller and RANN controller. It can be seen from the Table 1 that the proposed controller has the standout performance over the traditional PID controller.
are selected as 120, 0.0005, 100, and 0.01 respectively. The initial weights and thresholds in neural network are set as 0.01. It is clear from the experimental results that the tracking error is substantially reduced to nearly zero. The actual positions of the motors closely track the reference and tracking error converges to zero quickly. Moreover, the control input responses of X-axis and Y-axis shown in Figures 16 and 19 indicate the improvement of control effort of proposed controller, since it keeps the tracking error negligible during the motion path. On the contrary, the PID controller cannot produce sufficient torque command to keep tracking error of motor arbitrary small. Table 1 shows the comparison of the dynamic performance of the PID controller and RANN controller. It can be seen from the Table 1 that the proposed controller has the standout performance over the traditional PID controller.
From the experimental results, it is clear that by using the proposed controller, the convergence and stability of the servo system can be guaranteed despite the existence of model uncertainties and disturbances and the rotor angle follows its desired trajectory satisfactorily.
4. Conclusions
In this paper, a robust adaptive neural network controller has been successfully implemented for the X-Y table.

Figure 14. Position tracking response of X-axis using RANN controller.
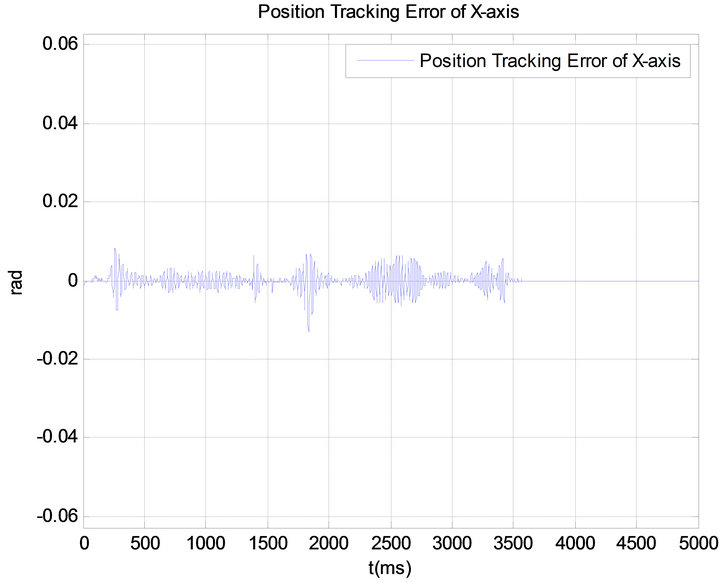
Figure 15. Position tracking error of X-axis using RANN controller.

Figure 16. Control input of X-axis using RANN controller.
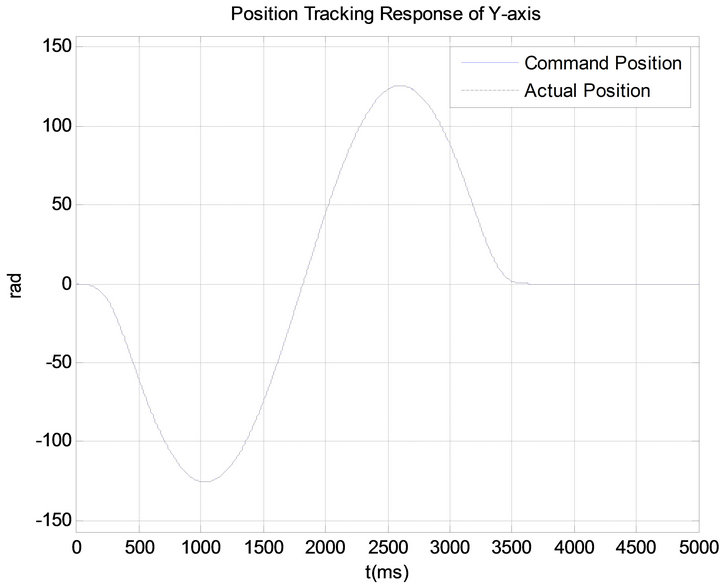
Figure 17. Position tracking response of Y-axis using RANN controller.
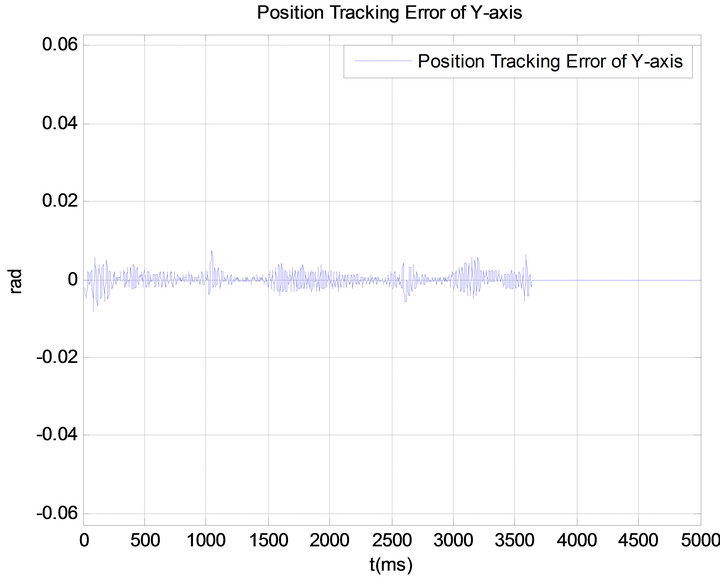
Figure 18. Position tracking error of Y-axis using RANN controller.
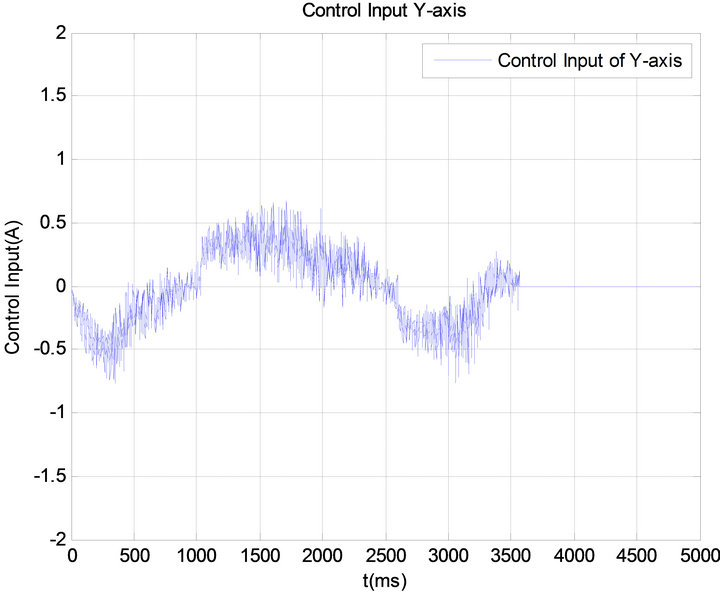
Figure 19. Control input of Y-axis using RANN controller.

Table 1. Comparison of PID and RANN controller.
The proposed schemes are designed by a systematic approach and implemented based on the high performance DSP TMS320C6727. Fast learning rule of the neural network and stable adaptive mechanism enable the controlller to overcome the nonlinear friction, uncertainties and disturbances of the mechanical system.
The stability and the convergence of the system are proved by Lyapunov theory and the validity of the controller is verified through experimental results.
REFERENCES
- H. Lim, J. W. Seo and C. H. Choi, “Position Control of XY Table in CNC Machining Center with Non-Rigid Ballscrew,” Proceedings of the American Control Conference, Chicago, 2000, pp. 1542-1546.
- E. C. Park, H. Lim and C. H. Choi, “Position Control of X-Y Table at Velocity Reversal Using Presliding Friction Characteristics,” IEEE Transactions on Control Systems Technology, Vol. 11, No. 1, 2003, pp. 24-31. doi:10.1109/TCST.2002.806436
- F. J. Lin and P. H. Shen, “Robust Fuzzy Neural Network Sliding-Mode Control for Two-Axis Motion Control System,” IEEE Transactions on Industrial Electronics, Vol. 53, No. 4, 2006, pp. 1209-1225. doi:10.1109/TIE.2006.878312
- Z. Jamaludin, H. Van Brussel and J. Swevers, “Friction Compensation of an XY Feed Table Using Friction-Model-Based Feedforward and an Inverse-Model-Based Disturbance Observer,” IEEE Transactions on Industrial Electronics, Vol. 56, No. 10, 2009, pp. 3848-3853. doi:10.1109/TIE.2009.2017560
- Y. T. Kim, “Adaptive Fuzzy Backstepping Control of AC Servo System in the Presence of Nonlinear Dynamic Effect and Mechanical Uncertainties,” Automation Congress, WAC, Hawaii, 28 September-2 October 2008, pp. 1-8.
- J. Chang, Y. Tan and J. T. Yu, “Backstepping Approach of Adaptive Control, Gain Selection and DSP Implementation for AC Servo System,” IEEE Power Electronics Specialists Conference, Orlando, 17-21 June 2007, pp. 535- 541.
- Y. S. Xiao, Q. D. Wu and G. X. Zhou, “Neural Network Based Parameters Identification and Adaptive Speed Control of AC Drive System,” Proceedings of the IEEE International Conference on in Industrial Technology, Shanghai, 2-6 December 1996, pp. 118-121.
- Y. X. Su, B. Y. Duan and Y. F. Zhang, “Robust Precision Motion Control for AC Servo System,” Proceedings of the 4th World Congress on Intelligent Control and Automation, Vol. 4, 2002, pp. 3319-3323.
- P. H. Kim, S. H. Sin, H. L. Baek and G. B. Cho, “Speed Control of AC Servo Motor Using Neural Networks,” Proceedings of the 5th International Conference on Electrical Machines and Systems, Shenyang, August 2001, pp. 691-694.
- K. Hornik, M. Stinchcombe and H. White, “Multilayer Feed-Forward Networks Are Universal Approximator,” Neural Networks, Vol. 2, No. 5, 1989, pp. 359-366. doi:10.1016/0893-6080(89)90020-8

