Intelligent Control and Automation
Vol. 3 No. 4 (2012) , Article ID: 24866 , 8 pages DOI:10.4236/ica.2012.34038
Adaptive Force Control of in Web Handling Systems
1Control Engineering, Lakehead University, Thunder Bay, Canada
2Mechanical Engineering, Lakehead University, Thunder Bay, Canada
Email: akadik@lakeheadu.ca, wwang3@lakeheadu.ca
Received June 17, 2012; revised July 16, 2012; accepted July 24, 2012
Keywords: Web Tension Control; Neural Fuzzy Approximator; Gain Scheduling; Winding/Unwinding Systems
ABSTRACT
Winding/unwinding system control is a very important issue to web handling machines. In this paper, a novel adaptive H∞ control strategy is developed for winding process control. A gain scheduling scheme is proposed based on a neural fuzzy approximator to improve the transient response and enhance tension control; the controller’s convergence and adaptive capability can be further improved by an efficient hybrid training algorithm. The effectiveness of the proposed adaptive H∞ control is verified by experimental tests. Test results show that the developed gain approximator can adaptively accommodate parameter variations in the system and improve the control performance.
1. Introduction
The term “web” refers to any material in a continuous flexible strip form, whose thickness is much less than its length and width, such as a paper, plastic film, textile, tape, metal plate. Web handling systems are used in a wide array of industries such as printing, pulp and paper, steel mills, and textile. An example is shown in Figure 1 as a multistage printing machine, which is a complicated, high-speed, and very expensive piece of equipment. The web is fed from an unwinding roll, transmitted though a series of intermediate units, and usually accumulated unto a winding roll. Web tension may vary from one span to another, due to the imperfections such as rotation nonsynchronization among the related drive motors, vibration, and mechanical/electrical defects in the system [1]. Excessive tension variations in web materials will degrade the production quality [2,3]. Correspondingly winding process control is a very important issue in web handling facilities to improve production quality, productivity, and reliability [4].
Several control strategies have been studied for winding systems, such as the decentralized control [5], distributed PI control with tension observers [6], noninteracting force control [7], as well as those based on softcomputing tools such as fuzzy logic and neural networks [8,9]. However, the classical control systems usually lack adaptive capability and robustness to accommodate for operation uncertainty and parameter variations. Although certain model-based feedforward loop compensation can be implemented to improve the robustness of web tension control, the effect of the compensation depends on the accuracy of the associated mathematical plant models. However, accurate analytical models are usually difficult to derive especially with parameter uncertainty, disturbances, and measurement noise.
Disturbance arises from various sources in a multistage web handling system, such as upstream tension fluctuations and web speed variations. On the other hand, in printing industries, for instance, different web materials may go through a given web-handling machine; that is, the operating characteristics change in operations. Furthermore, line speed variations will also have a strong influence on web tension control. When perturbations exist, robustness of the control system is desired. Baumgart et al. [10] suggested a robust control strategy based on the decoupled tension and speed loops of the nonlinear web model. Several H∞ controls were also proposed in [11-13] for web transportation system regulation. However, the effectiveness of these controllers heavily relies on the accuracy of the analytical gain scheduling that

Figure 1. An example of web-handling system: a multi-stage printing machine.
may lack adaptive capability to accommodate for some time-varying system characteristics in real-time applications.
To tackle the aforementioned problems, a new adaptive H∞ control strategy is developed in this work for winding process control. A novel gain scheduling scheme is proposed based on a neural fuzzy approximator to improve the transient response and enhance tension control; the adaptive capability of the controller is further improved by the use of a hybrid training strategy.
The remainder of the paper is organized as follows. Web system modeling is discussed in Section 2. The H∞ control and the related adaptive gain scheduling techniques are presented in Section 3. The effectiveness of the proposed control techniques is verified experimenttally in Section 4.
2. System Modeling
2.1. Plant Modeling
A simplified winding unwinding process is illustrated in Figure 2. To simplify analysis, the following assumptions are made [14,15]: 1) the thickness of the web is very small compared with the radius of winding/unwinding rollers; 2) the strain in the web is uniform within the web span; 3) the driving motors of winding and unwinding rolls have identical specifications; 4) no slip occurs between the web and the rollers; 5) neglecting dynamics of the load cell and idler rolls. The dynamics of the winding system can be derived as
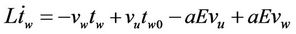 (1)
(1)
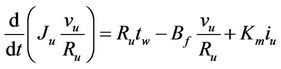 (2)
(2)
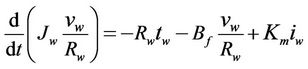 (3)
(3)
where tw = total web tension, N;
L = web length between winding and unwinding rolls, m;
Bf = coefficient of bearing viscous friction, Nm·s/rad;
Km = toque constant of the motors, N·m/A;
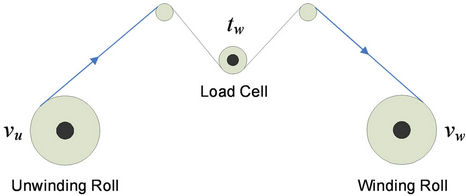
Figure 2. A simplified web handling process.
tw0 = wound-out tension of the unwinding roll, N;
vu, vw = tangential velocities of the unwinding and winding rolls, m/s;
iu, iw = input current to the driving motors of the unwinding and winding rolls, A;
Ru, Rw = radii of unwinding and winding rolls, m;
Ju, Jw = moments of inertia of the unwinding and winding rolls, kg·m2;
a, E = cross section area (m2) and Young’s modulus (GPa) of the web material.
The wound-out tension 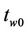 is an initial static tension within the web roll, which is generated by the previous winding and is assumed to be zero in this work for the sake of simplicity.
is an initial static tension within the web roll, which is generated by the previous winding and is assumed to be zero in this work for the sake of simplicity.
With the web material transmitted from the unwinding roll to the winding roll, the roll radius and inertia vary. If the winding and unwinding rolls have the same roll cores, the variations of the radius and inertia can be approximately described as
 (4)
(4)
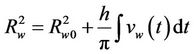 (5)
(5)
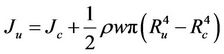 (6)
(6)
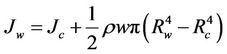 (7)
(7)
where
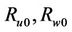 = initial radii of unwinding/winding rolls, m;
= initial radii of unwinding/winding rolls, m;
Rc, Jc = radius (m) and moment of inertia (kg·m2) of unwining winding roll core;
ρ, w, h = density (kg/m3), width (m), and thickness (m) of the web material, respectively.
Taking derivative of Equations (4)-(7) yields
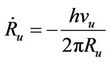 (8)
(8)
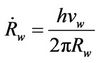 (9)
(9)
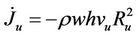 (10)
(10)
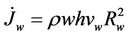 (11)
(11)
Substituting Equations (8)-(11) into (2) and (3) yields
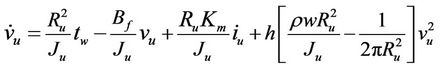 (12)
(12)
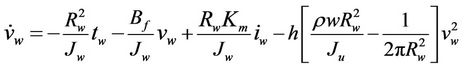 (13)
(13)
Since the web thickness h is much less than its width (e.g. the paper thickness is 0.0762 mm in this work), the last terms in Equations (12) and (13) can be neglected. The real-time model becomes S
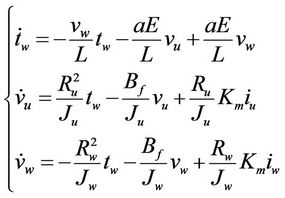 (14)
(14)
The state-space representation of the nominal winding process plant will be
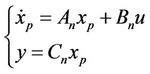 (15)
(15)
where the subscript p represents plant, n stands for nominal, and
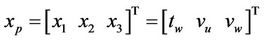
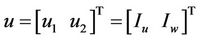
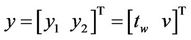
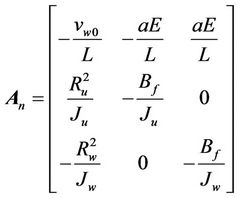
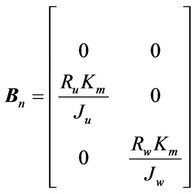
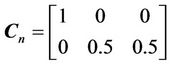
Matrix Cn is defined such that the outputs are the web tension and its line speed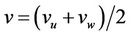 .
.
2.2. The Standard LFT Framework
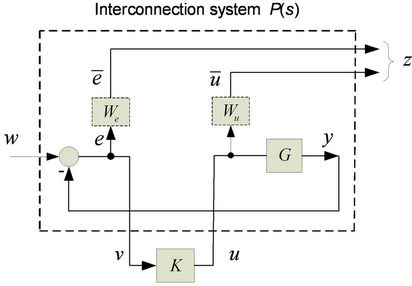
The practical connection of the closed-loop system with two weighting functions is illustrated in Figure 3(a), where P(s) is the interconnection system in the standard linear fractional transformation (LFT) framework as shown in Figure 3(b). The standard LFT framework in Figure 3(b) compactly describes the closed-loop system, whose exogenous input and output are w and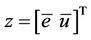 , respectively.
, respectively.
The weighting function We(s) aims to limit the magnitude of the output sensitivity function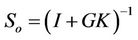 . With We(s), the H∞ norm of WeSo will be minimized by H∞ synthesis. In general, its desired value is limited to unity [16], that is,
. With We(s), the H∞ norm of WeSo will be minimized by H∞ synthesis. In general, its desired value is limited to unity [16], that is, 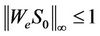 or
or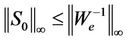 . We(s) is selected with a high gain at low frequency to reject low frequency perturbations
. We(s) is selected with a high gain at low frequency to reject low frequency perturbations
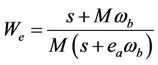 (16)
(16)
where M is the peak magnitude of S0,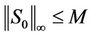 ;
; 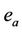 is the allowed steady-state error; and ωb is the required minimum frequency bandwidth.
is the allowed steady-state error; and ωb is the required minimum frequency bandwidth.
The control signal weighting function Wu(s) is selected to shape the frequency property of control signals
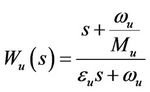 (17)
(17)
where Mu is the maximum gain of KS0, that is, 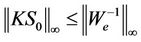 ; ωu is the bandwidth of the controller K; and εu is a real value to adjust the pole location of Wu.
; ωu is the bandwidth of the controller K; and εu is a real value to adjust the pole location of Wu.
The selection of weighting function and their numerical realization are based on the following considerations: 1) to achieve the desired control performance; 2) to op-
 (a)
(a)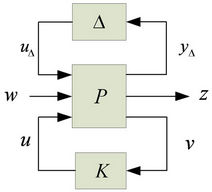 (b)
(b)
Figure 3. (a) The closed-loop system with weighting functions; (b) The standard LFT framework.
timize the control effort and avoid actuator saturation; 3) to obtain the best robustness property to the closed-loop system; and 4) to get the optimal balance among different robustness properties of the closed-loop system. By simulation, the frequency weighting functions We(s) and Wu(s) are determined as
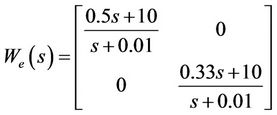 (18)
(18)
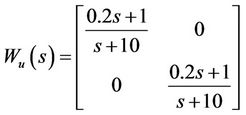 (19)
(19)
3. H∞ Synthesis and Gain Scheduling
3.1. H∞ Control Synthesis
H∞ synthesis is an optimization algorithm that aims to design an H∞ controller to achieve the desired robustness of the closed-loop system. Consider a nominal system represented by a lower LFT framework in Figure 4. The closed-loop transfer matrix can be represented as 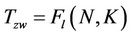 . The H∞ norm of the complex transfer matrix Tzw is defined as
. The H∞ norm of the complex transfer matrix Tzw is defined as
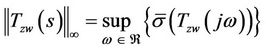 (20)
(20)
where 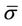 is the maximum singular value for a specific frequency ω, and
is the maximum singular value for a specific frequency ω, and 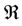 represents the collection of real numbers. The commonly adopted suboptimal H∞ control is described in [16]: Given γ > 0, find all admissible controllers
represents the collection of real numbers. The commonly adopted suboptimal H∞ control is described in [16]: Given γ > 0, find all admissible controllers  if there are any, such that
if there are any, such that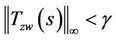 .
.
According to the selected weighting function 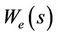 in (18), the conditions and assumption on a standard H∞ problem (as in [17]) are not satisfied. To tackle this problem, in this work, the initial controllers are designed based on the basic linear and time invariant model (15). One of the suboptimal H∞ controllers is derived for the considered general H∞ problem by solving two algebraic Riccati equations [16,18]. It can be represented by the following transfer function:
in (18), the conditions and assumption on a standard H∞ problem (as in [17]) are not satisfied. To tackle this problem, in this work, the initial controllers are designed based on the basic linear and time invariant model (15). One of the suboptimal H∞ controllers is derived for the considered general H∞ problem by solving two algebraic Riccati equations [16,18]. It can be represented by the following transfer function:
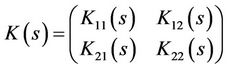 (21)
(21)
where
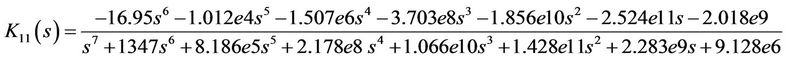
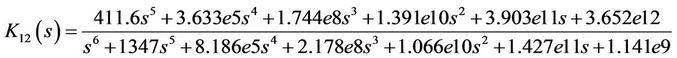
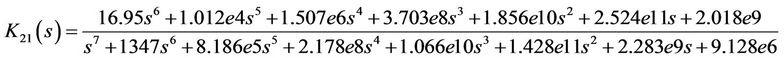
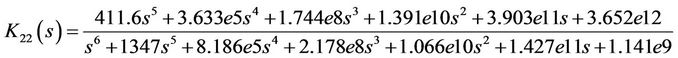
3.2. Neural Fuzzy Approximator for Gain Scheduling
Control system design for web handling processes is conducted based on the basic linear and time invariant model, in which all parameters take their nominal values at the specified operating point. However, the time varying parameters (e.g., roll radius and inertia) will influence the control performance and robustness property of the corresponding closed-loop system. Within the design region where both winding and unwinding rolls are around dimensionally half web loaded, the control performance is satisfactory. However, at starting and ending stages, tension output becomes rather sensitive to line speed variations. It is generally assumed in the literature that the impact from time varying parameters is not significant since the variation is small, especially when the web roll is small [13]. In this work, a neural fuzzy (NF) approximator is developed to adaptively estimate the gain values to improve tension control performance.
In this case, five input variables are used in the developed NF approximator: the radius of winding roll, radius of the unwinding roll, tension, web speed, and armature current signals for both the winding and unwinding motors. Three membership functions (MFs), small, medium, and large, are assigned to each input variable. The reasoning processing is performed in the following form:
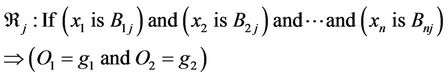 (22)
(22)
where 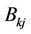 are MFs;
are MFs; 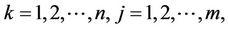 m is the number of rules.
m is the number of rules.
Figure 5 schematically shows the network architecture of the developed NF approximator. Unless specified, all
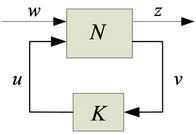
Figure 4. The LFT framework of nominal closed-loop system.
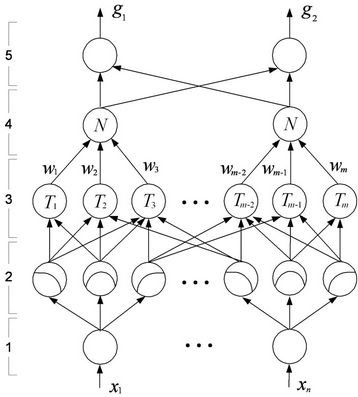
Figure 5. Network architecture of the NF approximator.
the network links have unity weights. The input nodes in layer 1 transmit the monitoring indices 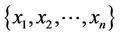 to the next layer, successively, where n = 5 in this case. Each node in layer 2 acts as an MF, which can be either a single node that performs a simple activation function or multilayer nodes that perform a complex function. The nodes in layer 3 perform the fuzzy T-norm operations. If a max-product operator is used, the firing strength of rule
to the next layer, successively, where n = 5 in this case. Each node in layer 2 acts as an MF, which can be either a single node that performs a simple activation function or multilayer nodes that perform a complex function. The nodes in layer 3 perform the fuzzy T-norm operations. If a max-product operator is used, the firing strength of rule 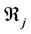 will be
will be
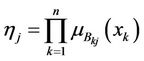 (23)
(23)
where 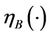 denote MF grades.
denote MF grades.
After normalization in layer 4, defuzzification is performed in layer 5. The predicted gain grades to each motor will be:
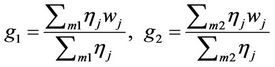 (24)
(24)
where 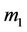 and
and 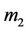 are the number of rules associated with the decisions of
are the number of rules associated with the decisions of 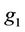 and
and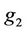 , respectively.
, respectively.
Correspondingly, the compensated input signals to the drive motors will be
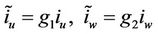 (25)
(25)
where 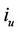 and
and 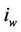 are the input current signals to the unwinding motor and winding motor, respectively.
are the input current signals to the unwinding motor and winding motor, respectively.
3.3. Online Training of the NF Approximator
Once the NF approximator is established, the related parameters should be optimized properly in order to achieve the desired input-output mapping. In training nonlinear system parameters, the classical method is the use of gradient algorithms [9]. The classical gradient algorithm, however, is slow in convergence especially when the approximation error becomes smaller [1]. To tackle this problem, an efficient fast gradient method, recently proposed in our research group [18], will be used in this work to optimize the nonlinear parameters of the NF approximator.
A hybrid training strategy is employed in this case to train the NF approximator. Each training epoch consists of two runs: in the backward pass, the nonlinear parameters of the NF approximator are updated by the fast gradient method [18]. In the backward pass, the linear parameters of the NF approximator, 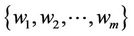 , are fine-tuned using a recurrent LSE method [1].
, are fine-tuned using a recurrent LSE method [1].
4. Evaluation and Comparison
In order to verify the effectiveness of the developed adaptive H∞ controller and the related techniques, a comparison study is taken in this section by experimental tests.
4.1. Experimental Setup
The experimental setup used in this work is shown in Figure 6, which has been developed by the authors’ research team. It consists of four DC motors and four idler rolls. Each motor can be controlled separately to simulate different drive/load conditions. Eight encoders (2048- lines) are used to measure shaft angular velocity. Tension can be measured by a tension transducer or an alternative spring-link-idler system. In this work, only two DC motors are set up as winding and unwinding rolls, whereas

Figure 6. Winding process experimental setup. (1) Alternative tension measurement system, (2) Winding roll, (3) DSP board, (4) Idler shaft, (5) Tension transducer, (6) Unwinding roll, (7) Encoder.
no control actions are provided in the intermediate zone.
The experiments are taken in two parts: tests in the middle stage of a winding process and tests in the starting stage of a winding process. In modeling, the radii of unwinding and wingding rolls can be approximately calculated by
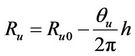 (24)
(24)
 (25)
(25)
where 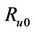 and
and 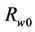 are the initial radii of unwinding and winding rolls, respectively;
are the initial radii of unwinding and winding rolls, respectively;  and
and 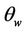 are the integrated angular displacements of the rolls; and h is the web thickness. Angular displacements are measured by two encoders mounted on the driving shafts of unwinding and winding rolls.
are the integrated angular displacements of the rolls; and h is the web thickness. Angular displacements are measured by two encoders mounted on the driving shafts of unwinding and winding rolls.
4.2. Middle Stage Experimental Test
In this test, both the winding roll and unwinding roll are operating around dimensionally half web wounded. The performance of the developed adaptive H∞ control is compared with a classical linear quadratic regulator (LQR) control. From our previous investigation [4], the LQR has been shown to outperform other related classical control modes (e.g., PI and PID) in web system control.
Figure 7 shows the test results of web tension control and line speed control by the developed adaptive H∞ control using the NF approximator and without using the NF approximator (i.e., the gains are estimated with the classical method as suggested in [13]). It is seen that the NF approximator can effectively predict the gain values and process the tension and speed control operations.
Figure 8 shows the corresponding results using the

Figure 7. Test result by using the adaptive H∞ control. (a), (b) Tension and speed using the NF approximator; (c), (d) Tension and speed using the classical gain scheduling.
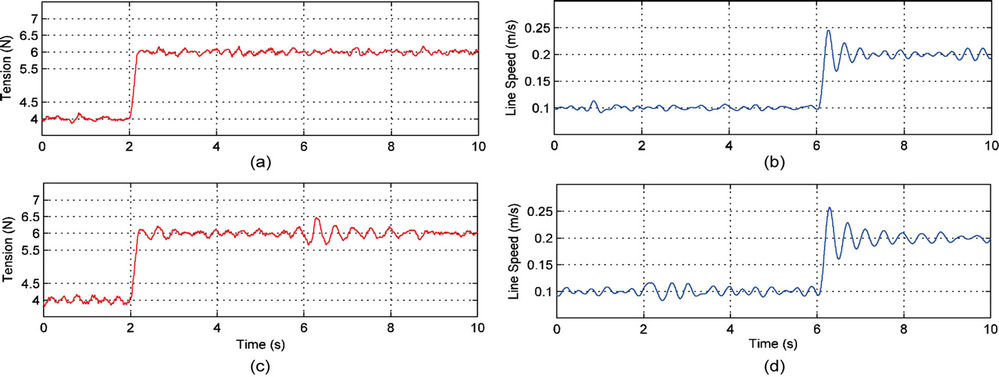
Figure 8. Test result by using the LQR control. (a), (b) Tension and speed using the NF approximator; (c), (d) Tension and speed using the classical gain scheduling.
LQR control with and without using the NF approximator. Comparing the corresponding results in Figure 7, the adaptive H∞ control outperforms the LQR in both force control and speed control, in terms of overshooting/undershooting and settling time. The proposed gain scheduling scheme can improve the control performance: specifically, 1) suppress the tension fluctuation due to line speed variations; 2) reduce the settling time for both tension and speed responses; and 3) the decrease overshot of speed response. The effectiveness of the classical gain scheduling method relies on the accuracy of the mathematical models, and the robustness to attenuate disturbances in web handling operations.
4.3. Starting Stage Experimental Test
In this test, the winding process is running from the starting point, at which the winding roll is web unloaded and the unwinding roll is fully web loaded. Figure 9 illustrates the test results by the adaptive H∞ control using the NF approximator and the classical gain scheduling methods, respectively. It is seen that the NF approximator can accommodate for more system uncertainty in gain scheduling, and provide more accurate control performance.
Figure 10 shows the control results using LQR control corresponding to different gain compensation strategies. Comparing Figures 8 and 9, it is clear the adaptive H∞ control is superior to the classical LQR control.
5. Conclusion
An adaptive H∞ control technique is developed in this paper for web handling system control, in which a neural
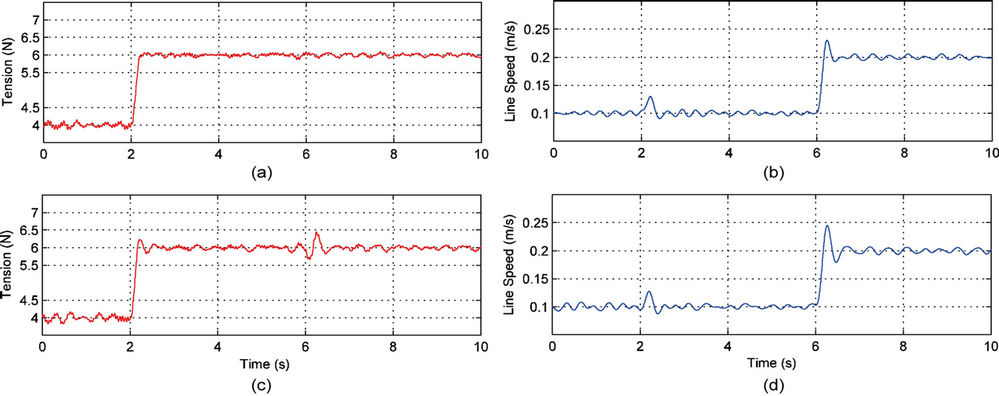
Figure 9. Test result by using the adaptive H∞ control. (a), (b) Tension and speed using the NF approximator; (c), (d) Tension and speed using the classical gain scheduling.

Figure 10. Test result by using the LQR control. (a), (b) Tension and speed using the NF approximator; (c), (d) Tension and speed using the classical gain scheduling.
fuzzy approximator is proposed to adaptively predict the gain values so as to improve transient performance in tension and line speed control. System convergence and adaptive capability can be further improved by an efficient hybrid training method. The viability of the developed H∞ control technique is verified by experimental tests. Test results have shown that the developed controller can effectively suppress the tension and speed fluctuations due to operation condition changes over the entire operating range of the winding process. The NF approximator can adaptively accommodate for parameter uncertainty, attenuate transient effects, and improve web tension control efficiency.
6. Acknowledgements
This work was partly financially supported by Materials and Manufacturing Ontario (MMO), Canada, and eMech Systems Inc.
REFERENCES
- W. Wang, “An Enhanced Diagnostic System for Gear System Monitoring,” IEEE Transactions on Systems, Man, Cybernetics, Part-B: Cybernetics, Vol. 38, No. 1, 2008, pp. 102-112. doi:10.1109/TSMCB.2007.908864
- W. Wang, F. Golanraghi and F. Ismail, “Condition Monitoring of Multistage Printing Presses,” Journal of Sound and Vibration, Vol. 260, 2004, pp. 755-766. doi:10.1016/S0022-460X(03)00209-8
- X. Dou and W. Wang, “Robust Control of Multistage Printing Systems,” Journal of ControlEngineering Practice, Vol. 18, No. 3, 2010, pp. 219-229. doi:10.1016/j.conengprac.2009.09.012
- K. Shin and S. Kwon, “The Effect of Tension on the Lateral Dynamics and Control of a Moving Web,” IEEE Transactions on Industry Applications, Vol. 43, No. 2, 2007, pp. 403-411. doi:10.1109/TIA.2006.889742
- P. Pagilla, N. Siraskar and R. Dwivedula, “Decentralized Control of Web Processing Lines,” IEEE Transactions on Control Systems Technology, Vol. 15, No. 1, 2007, pp. 106-117. doi:10.1109/TCST.2006.883345
- S. Song and S. Sul, “A New Tension Controller for Continuous Strip Processing Line,” IEEE Transactions on Industry Applications, Vol. 36, No. 2, 2000, pp. 633-639. doi:10.1109/28.833782
- G. Brandenburg, S. Geibenberger and A. Klemm, “Noninteracting Control of Web Force and Cut-Off Register Error in Rotary Printing Presses with Electronic Line Shafts,” EPE Journal, Vol. 16, 2006, pp. 38-44.
- D. Li and W. Wang, “A Novel Sliding Mode Controller for vibration Control in Flexible Structures,” Journal of Vibration and Control, Vol. 17, No. 14, 2011, pp. 2187- 2198. doi:10.1177/1077546311403181
- C. Wang, Y. Wang, R. Yang and H. Lu, “Research on Precision Tension Control System Based on Neural Network,” IEEE Transactions on Industrial Electronics, Vol. 51, No. 2, 2004, pp. 381-386. doi:10.1109/TIE.2003.822096
- M. Baumgart and L. Pao, “Robust Control of Nonlinear Tape Transport Systems with and without Tension Sensors,” Journal of Dynamic Systems, Measurement and Control, Vol. 129, No. 1, 2007, pp. 41-55. doi:10.1115/1.2397151
- H. Koc, D. Knittel, M. de Mathelin and G. Abba, “Modeling and Robust Control of Winding Systems for Elastic Webs,” IEEE Transactions on Control Systems Technology, Vol. 10, No. 2, 2002, pp. 197-208. doi:10.1109/87.987065
- D. Knittel, E. Laroche, D. Gigan and H. Koc, “Tension Control for Winding Systems with Two-Degrees-ofFreedom H-Infinity Controllers,” IEEE Transactions on Industry Applications, Vol. 39, No. 1, 2003, pp. 113-120. doi:10.1109/TIA.2002.807231
- E. Laroche and D. Knittel “An Improved Linear Fractional Model for Robustness Analysis of a Winding System”, Control Engineering Practice, Vol. 13, 2005, pp. 659-666. doi:10.1016/j.conengprac.2004.05.008
- K. Shin, “Tension Control,” TAPPI Press, Raleigh, 2000.
- K. Zhou and J. Doyle, “Essentials of Robust Control,” Prentice Hall, Prentice Hall, 1998.
- R. Beaven, M. Wright and D. Seaward, “Weighting Function Selection in the Design Process,” Control Engineering Practice, Vol. 4, No. 5, 1996, pp. 625-633. doi:10.1016/0967-0661(96)00044-5
- K. Lin, “Observer-Based Tension Feedback Control with Friction and Inertia Compensation,” IEEE Transactions on Control Systems Technology, Vol. 11, No. 1, 2003, pp. 109-118. doi:10.1109/TCST.2002.806464
- W. Wang, D. Li and J. Vrbanek, “An Adaptive Evolving Technique for System Dynamic State Analysis,” Journal of Neurocomputing, Vol. 85, 2012, pp. 111-119. doi:10.1016/j.neucom.2012.02.006

