Intelligent Control and Automation
Vol. 3 No. 2 (2012) , Article ID: 19240 , 9 pages DOI:10.4236/ica.2012.32018
An Output Stabilization Problem of Distributed Linear Systems Approaches and Simulations
Department of Mathematics and Computer science, Faculty of Science, University of Moulay Ismaïl, Meknès, Morocco
Email: {zerrik3, bensyassine}@yahoo.fr
Received February 13, 2012; revised March 20, 2012; accepted March 28, 2012
Keywords: Distributed System; Gradient Stability; Gradient Stabilization; Stabilizing Control
ABSTRACT
The goal of this paper is to study an output stabilization problem: the gradient stabilization for linear distributed systems. Firstly, we give definitions and properties of the gradient stability. Then we characterize controls which stabilize the gradient of the state. We also give the stabilizing control which minimizes a performance given cost. The obtained results are illustrated by simulations in the case of one-dimensional distributed systems.
1. Introduction
One of the most important notions in systems theory is the concept of stability. An equilibrium state is said to be stable if the system remains close to this state for small disturbances; and for an unstable system the question is how to stabilize it by a feedback control.
For finite dimensional systems, the problem of stabilization was considered in many works and various results have been developed [1]. In the infinite dimensional case, the problem has been treated in Balakrishnan [2], Curtain and Zwart [3], Pritchard and Zabczyk [4], Kato [5], Triggiani [6]. Many approaches have been considered to characterize different kinds of stabilization for linear distributed systems: Lyapunov and Riccati equation for exponential stabilization, and dissipative type criterion for the case of strong stabilization [3-5,7]. The problem has been also treated by means of specific state space decomposition [6]. The above results concern the state, but in many real problem the stabilization is considered for the state gradient of the considered system, which means to find a feedback control such that the gradient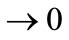 , when
, when 
For example the problem of thermal insulation where the purpose is to keep a constant temperature of the system with regards to the outside environment assumed to be with fluctuating temperature. Thus one has to regulate the system temperature in order to vanish the exchange thermal flux. This is the case inside a car where one has to change the level of the internal air conditioning with respect to the external temperature.
As we cannot always have external measurements, we use a sensor to measure the flux, which is a transducer producing a signal that is proportional to the local heat flux.
The purpose of this paper is the study of gradient stabilization. It is organized as follows: In the second section we define and characterize gradient stability. In the third section, we characterize gradient stabilizability, by finding a control that stabilizes the gradient of a linear distributed system and we give characterizations of such a control. In the fourth section we search the minimal cost control that stabilizes the system gradient. In the last section we give an algorithmic approach for control implementation and simulation examples.
2. Gradient Stability
This section is devoted to some preliminaries concerning definition and characterization of gradient stability for linear distributed systems.
2.1. Notations and Definitions
Let 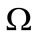 be an open regular subset of
be an open regular subset of 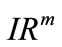 and let us consider the state-space system
and let us consider the state-space system
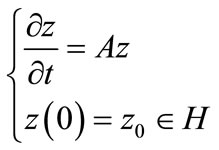 (1)
(1)
where 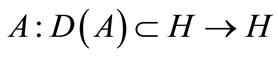 is a linear operator generating a strongly continuous semigroup
is a linear operator generating a strongly continuous semigroup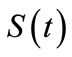 ,
, 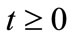 , on the state space H which is continuously embedded in
, on the state space H which is continuously embedded in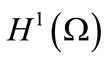 .
.
H is endowed with its a complex inner product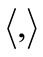 . and the corresponding norm
. and the corresponding norm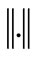 .
.
We define the operator  by:
by:
 (2)
(2)
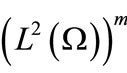 is endowed with its usual complex inner product
is endowed with its usual complex inner product  and the corresponding norm
and the corresponding norm 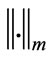 where:
where:
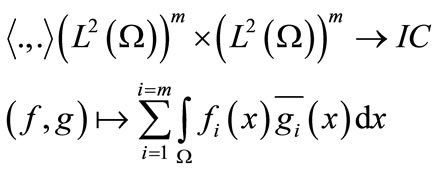 (3)
(3)
With 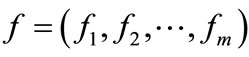 and
and 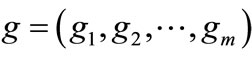 where
where 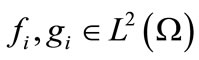
 The mild solution of (1) is given by
The mild solution of (1) is given by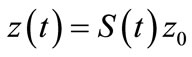 .
.
Let  denote the adjoint operator of
denote the adjoint operator of , and we define the operator
, and we define the operator 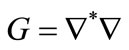 which a bounded operator applying H into itself.
which a bounded operator applying H into itself.
Definition 2.1
The system (1) is said to be
• Gradient weakly stable (g.w.s) if , the corresponding solution
, the corresponding solution  of (1) satisfies
of (1) satisfies
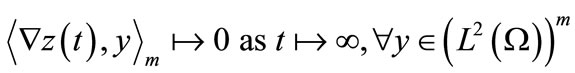
• Gradient strongly stable (g.s.s) if for any initial condition 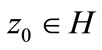 the corresponding solution
the corresponding solution 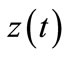 of (1) satisfies:
of (1) satisfies:
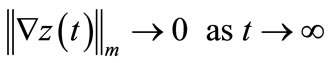
• Gradient exponentially stable (g.e.s) if there exist M, 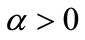 such that:
such that:
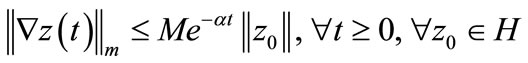
Remark 2.2
From the above definitions we have:
1) g.e.s 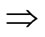 g.s.s
g.s.s 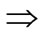 g.w.s.
g.w.s.
2) If the system (1) is stable then it also gradient stable.
3) We can find systems gradient stable but not stable. This is illustrated in the following example.
Exemple 2.3
Let , on
, on  we consider the following system
we consider the following system
 (4)
(4)
Where  and
and 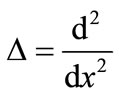 is the Laplace operator.
is the Laplace operator.
The eigenpairs 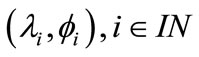 of A are given by:
of A are given by:
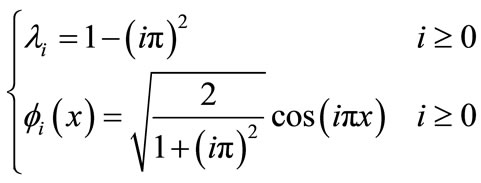
A generates a strongly continuous semigroup  given by
given by

 then (4) isn’t stable but
then (4) isn’t stable but
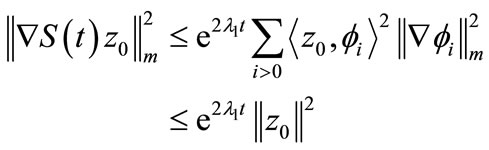
Therefore the system (4) is g.e.s.
2.2. Characterizations
The following result links gradient stability of the system (1) to the spectrum properties of the operator A.
Let us consider the sets
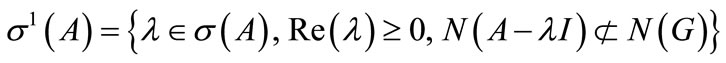
and
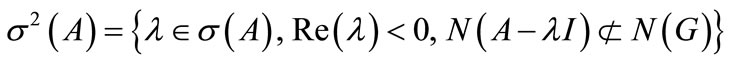
where 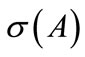 and
and 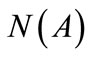 are the points spectrum and the kernel of the operator A.
are the points spectrum and the kernel of the operator A.
Proposition 2.4
1) If the system (1) is g.w.s then 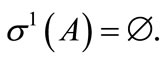
2) Assume that the state space H has an orthonormal basis 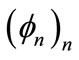 of eigenfunctions of A, if
of eigenfunctions of A, if 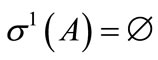 and, for some
and, for some ,
,  for all
for all 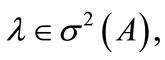 then the system (1) is g.e.s.
then the system (1) is g.e.s.
Proof
1) Assume that there exists  such that
such that 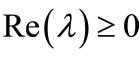 and there exists
and there exists 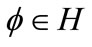 such that
such that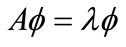 .
.
For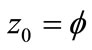 , the solution of (1) is
, the solution of (1) is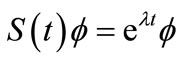 , so
, so
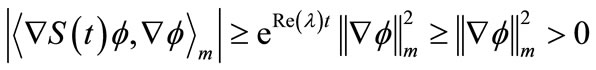
hence the system (1) is not g.w.s.
2) For 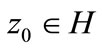 we have
we have

where  is the multiplicity of the eigenvalue
is the multiplicity of the eigenvalue 
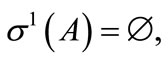 gives:
gives:
 for some
for some 
So we have the g.e.s of the system (1).
As example we consider (4). We have: 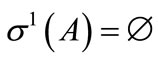 and
and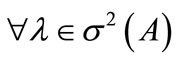 ,
,  , then the system (4) is g.e.s.
, then the system (4) is g.e.s.
For the gradient exponential stability, we need the following lemma.
Lemma 2.5
Assume that there exists a function  such that:
such that:
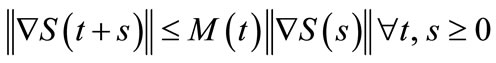 (5)
(5)
Then the operators  are uniformly bounded.
are uniformly bounded.
Proof
Let us show that . Otherwise there exists a sequence
. Otherwise there exists a sequence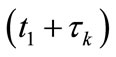 ,
, 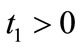 and
and 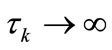 such that
such that 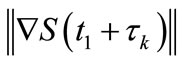 is increasing without bound.
is increasing without bound.
Now we have:
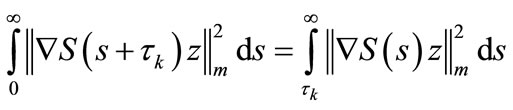
and the right-hand side goes to zero when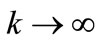 .
.
By Fatou’s lemma 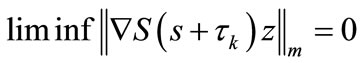 when
when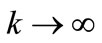 , almost everywhere
, almost everywhere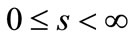 .
.
Hence for some  we can find a subsequence
we can find a subsequence 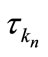 such that
such that 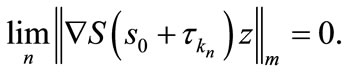
But with (5) we have
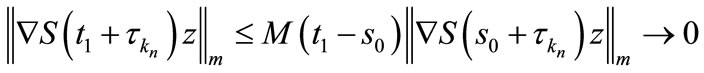
when  which is a contradiction.
which is a contradiction.
The conclusion follows from the uniform boundedness principle.
Proposition 2.6
Assume that (5) is satisfied and
 (6)
(6)
Then the system (1) is g.e.s if and only if
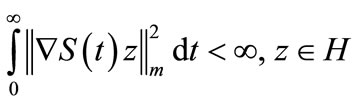
Proof
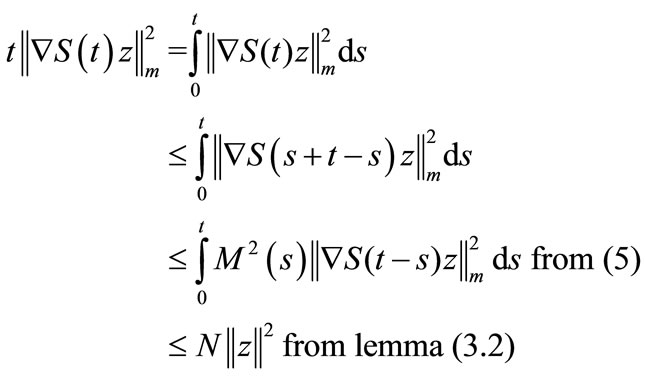
where , then
, then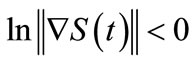 ,
, 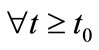 for some
for some 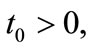 hence
hence
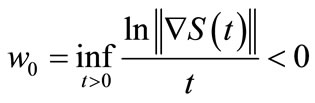
Now we show that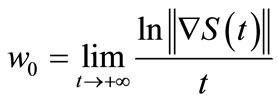 .
.
Let t1 > 0, and 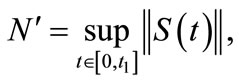 there exists
there exists 
such that 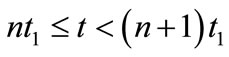 for each
for each 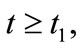 then
then

With (4) we have
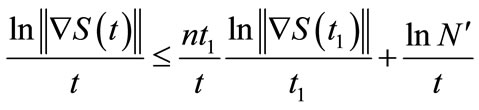
Therefore
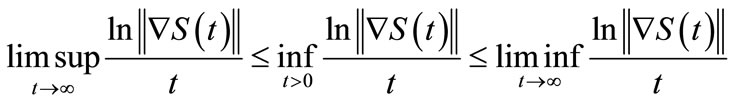
then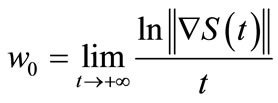 .
.
Hence for all  there exists M' such that
there exists M' such that
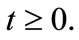

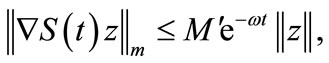
So the system (1) is g.e.s.
The converse is immediate.
Example 2.7
The system (2) satisfies the conditions (5) and (6). Indeed:
Let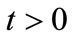 , and
, and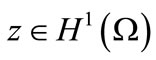 .
.
We have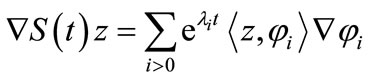 , which implies
, which implies
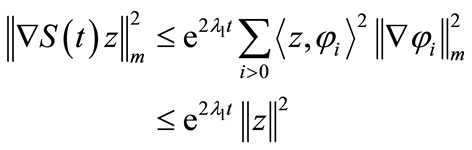
we can show that 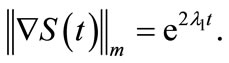
We have .
.
Therefore the system (4) is g.e.s.
Corollaire 2.8
Under conditions (5) and (6) and assume, in addition, that there exists a self-adjoint positive operator 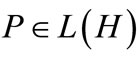 such that:
such that:
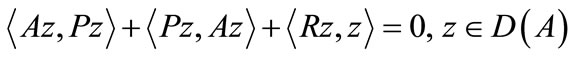 (7)
(7)
where 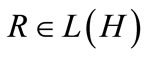 is a self-adjoint operator satisfying
is a self-adjoint operator satisfying
 (8)
(8)
then (1) is g.e.s.
Proof
We define the function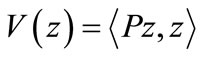 ,
, 
For 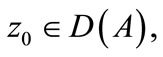 we have
we have 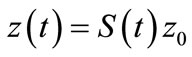 and
and

Thus  By (8), we obtain
By (8), we obtain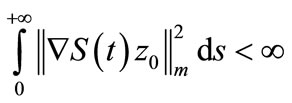 .
.
Since 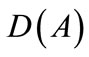 is dense in H we can extended this inequality to all
is dense in H we can extended this inequality to all 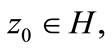 and the proposition 3.3 gives the conclusion.
and the proposition 3.3 gives the conclusion.
For the gradient strong stability we have the following result.
Proposition 2.9
Assume that the equation
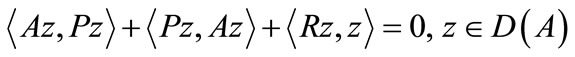
has a self-adjoint positive solution 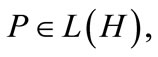 where
where  is a self-adjoint operator satisfying (8). Moreover if the following condition holds
is a self-adjoint operator satisfying (8). Moreover if the following condition holds
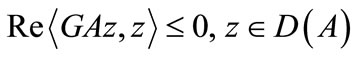 (9)
(9)
then (1) is g.s.s.
Proof
Let us consider the function:

For , we have
, we have 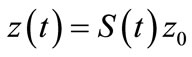 and
and

we obtain 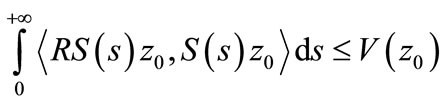 By (8),
By (8), 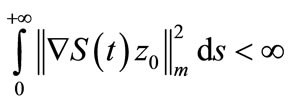 and from (9), we have
and from (9), we have
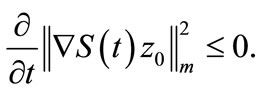
Then

We deduce
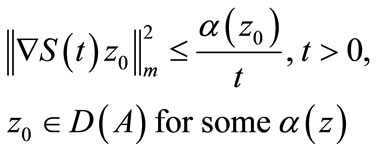 (10)
(10)
From the density of 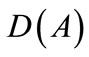 in H, and the continuity of
in H, and the continuity of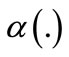 , (10) is satisfied for all
, (10) is satisfied for all . This means that the gradient of (1) is strongly stable.
. This means that the gradient of (1) is strongly stable.
3. Gradient Stabilizability
Let us consider the system
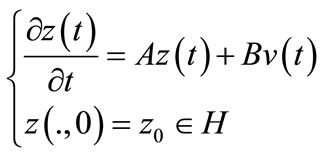 (11)
(11)
with the same assumptions on A, and B is a bounded linear operator mapping U, the space of controls (assumed to be Hilbert space), into H.
Definition 3.1
The system (11) is said to be gradient weakly (respectively strongly, exponentially) stabilizable if there exists a bounded operator  such that the system
such that the system
 (12)
(12)
is g.w.s (respectively g.s.s, g.e.s).
Remark 3.2
1) If a system is stabilizable, then it is also gradient stabilizable.
2) Gradient stabilizability is cheaper than state stabilizability. Indeed if we consider the cost functional

and the spaces
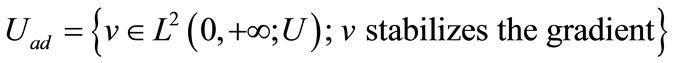
and
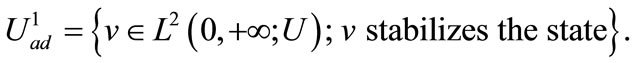
Then we have 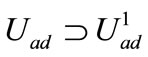 and therefore
and therefore
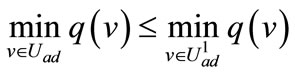
3) The gradient stabilization may be seen as a special case of output stabilization with output operator .
.
In the following we give the feedback control which stabilizes the gradient of the system (11), by two approaches.
The first is an extension of state space decomposition [6] and the second one is based on algebraic Riccati equation.
3.1. Decomposition Method
Let 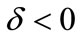 be a fixed real and consider the subsets
be a fixed real and consider the subsets  and
and  of the spectrum
of the spectrum 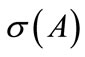 of A defined by
of A defined by
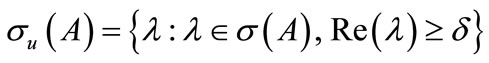
and
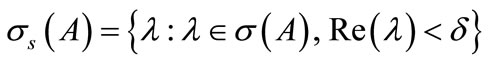
Assume that  is bounded and is separated from the set
is bounded and is separated from the set 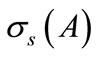 in such a way that a rectifiable simple closed curve can be drawn so as to enclose an open set containing
in such a way that a rectifiable simple closed curve can be drawn so as to enclose an open set containing 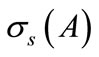 in its interior and
in its interior and 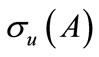 in its exterior. This is the case, for example, where A is selfadjoint with compact resolvent, there are at most finitely many nonnegative eigenvalues of A and each with finite dimensional eigenspace.
in its exterior. This is the case, for example, where A is selfadjoint with compact resolvent, there are at most finitely many nonnegative eigenvalues of A and each with finite dimensional eigenspace.
Then the state space H can be decomposed [5] according to:
 (13)
(13)
with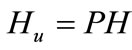 ,
, 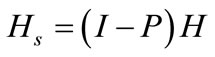 , and
, and 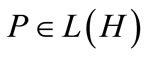 is the projection operator given by
is the projection operator given by 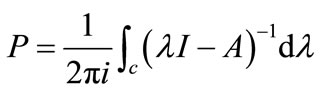
where C is a closed curve surrounding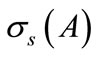 .
.
The system (11) may be decomposed into the two subsystems
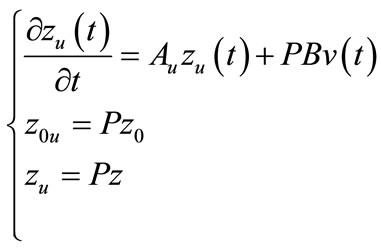 (14)
(14)
and
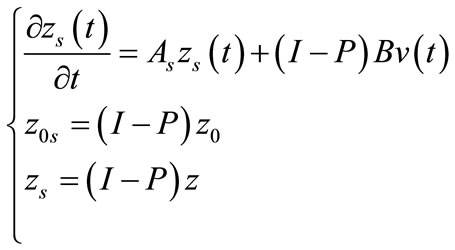 (15)
(15)
where  and
and 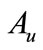 are the restrictions of A to
are the restrictions of A to  and
and , and are such that
, and are such that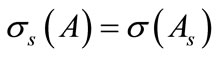 ,
,  , and
, and 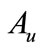 is a bounded operator on Hu.
is a bounded operator on Hu.
The solutions of (14) and (15) are given by
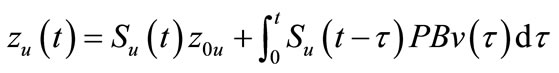 (16)
(16)
And
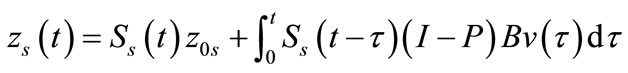 (17)
(17)
where 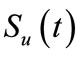 and
and 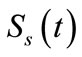 denote the restriction of
denote the restriction of  to
to  and
and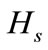 , which are strongly continuous semigroups generated by
, which are strongly continuous semigroups generated by 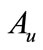 and
and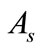 .
.
For the system state, it is known (see [6]) that if the operator 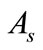 satisfies the spectrum growth assumption
satisfies the spectrum growth assumption
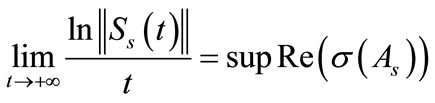 (18)
(18)
then stabilizing (11) comes back to stabilize (14).
The following proposition gives an extension of this result to the gradient case.
Proposition 3.3
Let the state space satisfy the decomposition (13) and 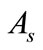 satisfy the following inequality
satisfy the following inequality
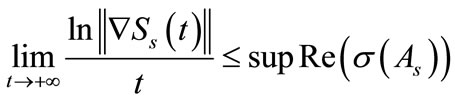 (19)
(19)
1) If the system (14) is gradient exponentially (respectively strongly) stabilizable by a feedback control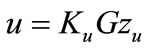 , with
, with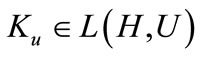 , then the system (11) is gradient exponentially (respectively strongly) stabilizable using the control
, then the system (11) is gradient exponentially (respectively strongly) stabilizable using the control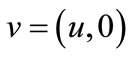 .
.
2) If the system (14) is gradient exponentially (resp strongly) stabilizable by the feedback control:  with
with 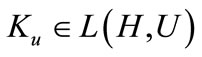 then the system (11) is gradient exponentially (respectively strongly) stabilizable using the feedback operator
then the system (11) is gradient exponentially (respectively strongly) stabilizable using the feedback operator .
.
Proof
We give the proof for the exponential case. In view of the above decomposition, we have: .
.
Hence if 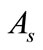 satisfies (19) then for some
satisfies (19) then for some 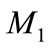 and
and , we have:
, we have: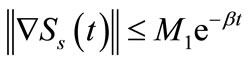 ,
,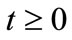 .
.
It follows that the system (15) is gradient exponentially stabilizable taking v(t) = 0.
Let 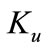 be such that
be such that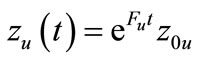 , with
, with
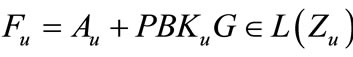 and there exists
and there exists , M2 > 0 such that
, M2 > 0 such that 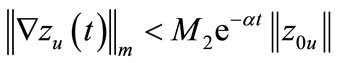
Then with the feedback control 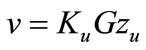 we have
we have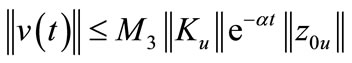 , with
, with 
From (17) and (18) we have
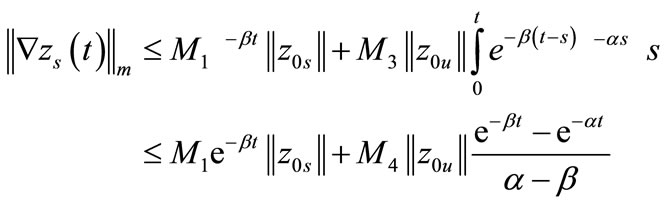
with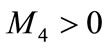 .
.
Thus the system (11) excited by 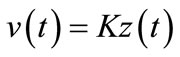 satisfies
satisfies
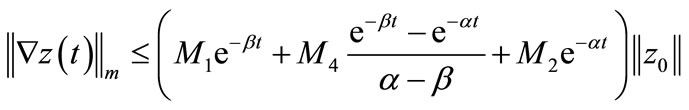
which shows that the system (11) is gradient exponentially stabilizable.
2) The case of strong stabilizability follows from similar above techniques.
Corollary 3.4
Let A satisfy the spectrum decomposition assumption (13) and suppose that (19) is satisfied. If in addition 1)  is a finite dimensional space 2) The system (14) is controllable on
is a finite dimensional space 2) The system (14) is controllable on  then the system (11) is gradient exponentially stabilizable.
then the system (11) is gradient exponentially stabilizable.
Proof
The system (14) is of finite dimension and is controllable on the space 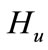 then it is stabilizable on the same space, hence it is gradient stabilizable, the conclusion is obtained with the proposition 3.3.
then it is stabilizable on the same space, hence it is gradient stabilizable, the conclusion is obtained with the proposition 3.3.
3.2. Riccati Method
Let us consider the system (11) with the same assumptions on A and B. We denote by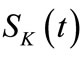 ,
,  the strongly continuous semigroup generated by
the strongly continuous semigroup generated by , where K is the feedback operator
, where K is the feedback operator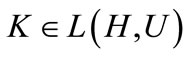 .
.
Let 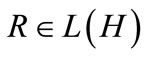 be a self-adjoint operator such that (8) is satisfied and suppose that the steady state Riccati equation
be a self-adjoint operator such that (8) is satisfied and suppose that the steady state Riccati equation
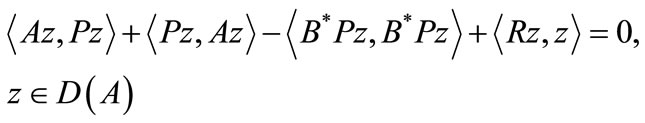 (20)
(20)
has a self-adjoint positive solution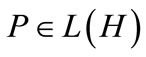 , and let
, and let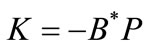 .
.
Proposition 3.5
1) If 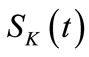 satisfies the conditions (5) and (6), then the system (11) is gradient exponentially stabilizable by the control
satisfies the conditions (5) and (6), then the system (11) is gradient exponentially stabilizable by the control 
2) If 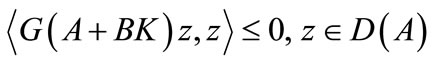 then the system (11) is gradient strongly stabilizable.
then the system (11) is gradient strongly stabilizable.
3) Suppose that the system (11) is gradient exponentially stabilizable. If in addition the feedback operator K satisfies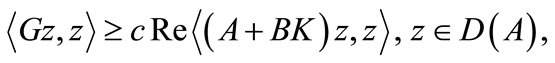 for some c > 0 then the state of the system (12) remains bounded.
for some c > 0 then the state of the system (12) remains bounded.
Proof
The first and second points are deduced from the second section.
For the thirst point: Let 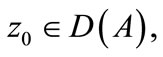 we have
we have
 (21)
(21)
and from (21) we obtain
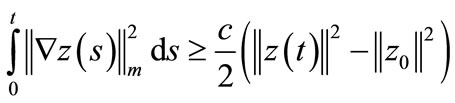
Since the system (11) is gradient exponentially stabilizable then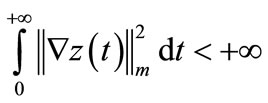 , so there exists
, so there exists 
such that 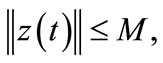 for all
for all 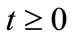 and by the density of
and by the density of 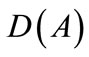 in H we have the conclusion.
in H we have the conclusion.
3.3. Gradient Stabilization Control Problem
Here we explore the control that stabilizes the gradient of the system (11) as a solution of the minimization problem
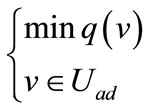 (22)
(22)
where  with
with

and R is a linear bounded operator mapping H into itself and satisfying (8).
We recall the classical result known for state stabilization if 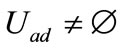 for each initial state
for each initial state 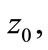 then there exists a unique control
then there exists a unique control 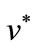 that minimizes (22) and given by
that minimizes (22) and given by  where P is a positive solution of the steady state Riccati Equation (20).
where P is a positive solution of the steady state Riccati Equation (20).
If in addition the operator R is coercive then the state of system (11) is exponentially stabilizable (see [7]).
In the following we give an extension of the above result to the gradient case.
We suppose that  for each initial state
for each initial state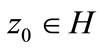 , and R satisfies (8).
, and R satisfies (8).
Proposition 3.6
The control given by 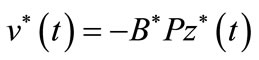 minimizes
minimizes  where P assumed to be a self-adjoint, positive operator, and satisfies the steady state Riccati equation (20), if in addition the semigroup
where P assumed to be a self-adjoint, positive operator, and satisfies the steady state Riccati equation (20), if in addition the semigroup  satisfies the conditions (5) and (6) then the same control stabilizes the gradient of system (11)
satisfies the conditions (5) and (6) then the same control stabilizes the gradient of system (11)
Proof
The proof follows from [7], and the proposition 3.5.
4. Numerical Algorithm and Simulations
In this section we present an algorithm which allows the calculation of the solution of problem (22) stabilizing the gradient of the system (11). By the previous result this control may be obtained by solving the algebraic Riccati Equation (20). Let 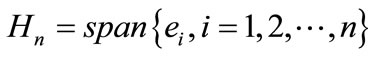 where
where 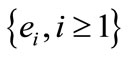 is a hilbertian basis of H.
is a hilbertian basis of H.  is a subspace of H endowed with the restriction of the inner product of H. The projection operator
is a subspace of H endowed with the restriction of the inner product of H. The projection operator 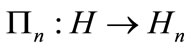 is defined by
is defined by
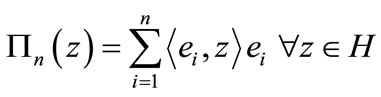
The projection of (20) on space , is given formally by:
, is given formally by:
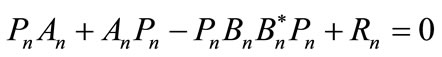 (23)
(23)
where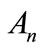 ,
,  and
and 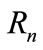 are respectively the projections of A, P and R on
are respectively the projections of A, P and R on , and
, and 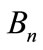 the projection of B which is mapping U the space of control into
the projection of B which is mapping U the space of control into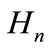 .
.
We have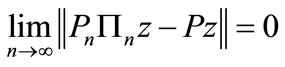 , that is
, that is 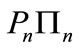 converges to P strongly in H, (see [8]).
converges to P strongly in H, (see [8]).
We can write the projection of (11) like
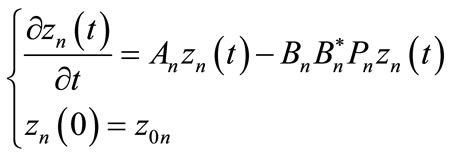 (24)
(24)
the solution of this system is given explicitly by:
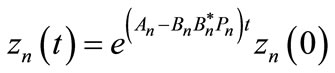 (25)
(25)
To calculate the matrix exponential we use the Padé approximation with scaling and squaring (see [9]).
If we denote , we have
, we have
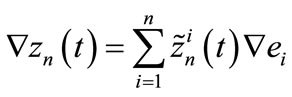 (26)
(26)
Let consider a time sequence ,
, 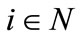 where
where 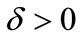 small enough.
small enough.
With these notations, the gradient stabilization control may be obtained the algorithm steps (Table 1).
Remark 4.1
The dimension of the projection space n is choosing to be good approximation of the considered system and appropriate for numerical constraint.
Example 4.2
Let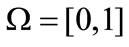 , on
, on
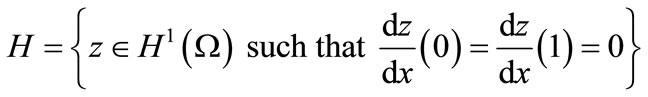
which is an Hilbert space we consider the following system
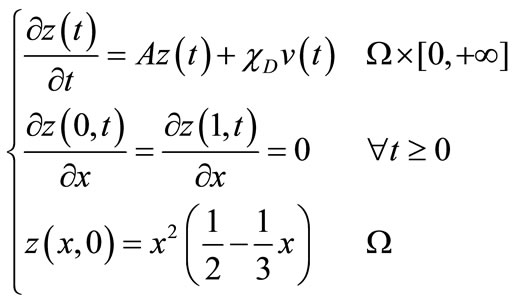 (27)
(27)
where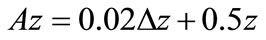 ,
, 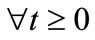
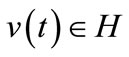 ,
, 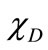 is the restriction operator on
is the restriction operator on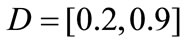 , and we consider the problem (22) with
, and we consider the problem (22) with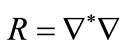 .
.
A generates a strongly continuous semigroup 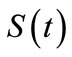
given by: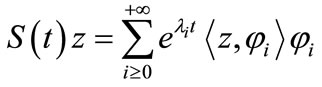 , where
, where
 and
and  with
with
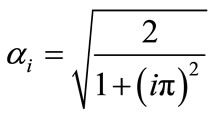 .
.
The state and the gradient of system (27) are unstable since .
.
Let consider the subspace

Applying the algorithm taking the truncation at n = 5, we obtain figures 1 which illustrates the evolution of the system gradient and shows how the gradient evolves close to zero when the time t increases.
The gradient is stabilized with error equals 9.9836 × 10–7 and cost equals 2.6982 × 10–4. This shows the efficiency of the developed algorithm.
In table 2 we give the cost of gradient stabilization of system (27) for different supports control “D”.
The Table 2 shows that there is relation between area of control support and the cost of gradient stabilization, more precisely more this area decreases more cost in-

Table 1. Algorithm.
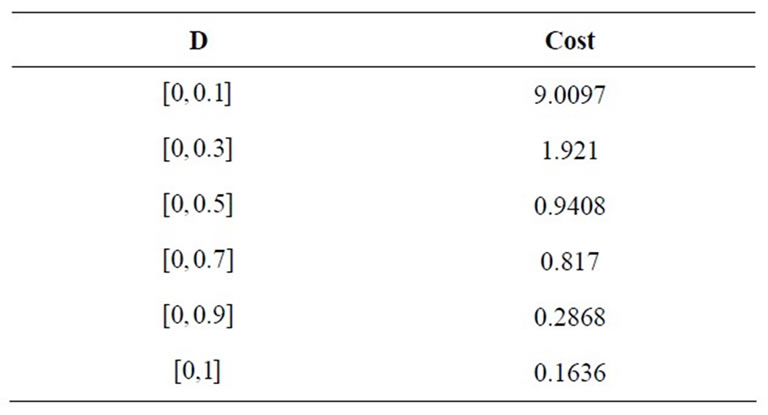
Table 2. Support control-cost stabilization.

Figure 1. The gradient evolution for the Neumann boundary condition case.
creases.
Example 4.3
Let  on
on  we consider the system (27) with Dirichlet boundary conditions:
we consider the system (27) with Dirichlet boundary conditions:
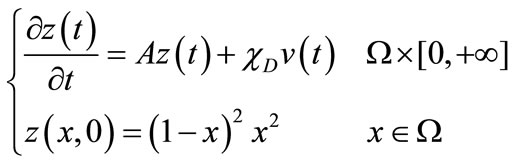 (28)
(28)
where ,
, 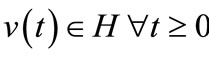 ,
, 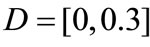 , and we consider the problem (22) with
, and we consider the problem (22) with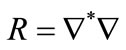 .
.
The eigenpairs of A are given by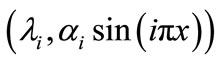 ,
, 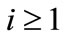 , with
, with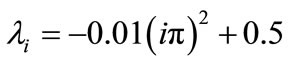 .
.
The state and the gradient of system (28) are unstable since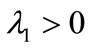 .
.
We consider the subspace
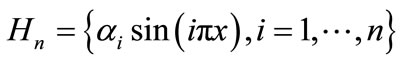 with
with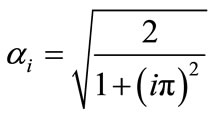 .
.
Applying the algorithm with truncation (n = 5), the figure 2 shows the gradient evolution at times t = 3, 5, and 13.
In table 3 we present the cost of gradient stabilization

Figure 2. The gradient evolution for the Direchlet boundary condition case.
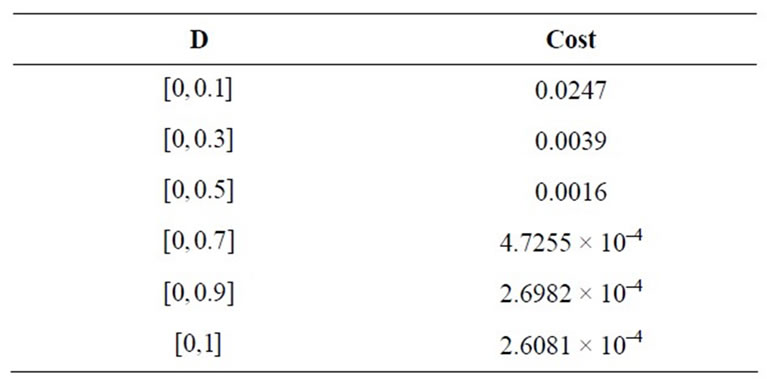
Table 3. Support control-cost stabilization.
of system (28) for different zone control support “D”.
Also in this example, we remark that more the area of control support increases more the cost of gradient stabilization decreases.
4. Conclusions
In this paper the question of gradient stabilization is explored. According to the conditions, satisfied by the dynamic of system, and those satisfied by the state space, two methods are applied to characterize the controls of gradient stabilization namely, decomposition approach and Riccati method.
The obtained results are successfully illustrated by numerical simulations. Questions are still open, this is the case of regional gradient stabilization. It is under consideration and will be appear in separate paper.
5. Acknowledgements
The work presented here was carried out within the support of the Academy Hassan II of Sciences and Technology.
REFERENCES
- W. M. Wonham, “Linear multivariable Control: A Geometric Approach,” Springer-Verlag, Berlin, 1974.
- A. V. Balakrishnan, “Strong stabilizabity and the Steady State Riccati Equation,” Applied Mathematics and Optimization, Vol. 7, No. 1, 1981, pp. 335-345. doi:10.1007/BF01442125
- R. F. Curtain and H. J. Zwart, “An Introduction to Infinite Dimensional Linear Systems Theory,” SpringerVerlag, Berlin, 1995.
- A. J. Pritchard and J. Zabczyk, “Stability and Stabilizability of Infinite Dimensional Systems,” Siam Review, Vol. 23, No.1, 1981, pp. 25-51. doi:10.1137/1023003
- T. Kato, “Perturbation theory for Linear Operators,” Springer-Verlag, Berlin, 1980.
- R. Triggiani, “On the Stabilizability Problem in Banach Space,” Journal of Mathematical Analysis and Applications, Vol. 52, No. 3, 1979, pp. 383-403. doi:10.1016/0022-247X(75)90067-0
- R. F. Curtain, and A. J. Pritchard, “Infinite Dimensional Linear Systems Theory,” Springer-Verlag, Berlin, 1978.
- H. T. Banks and K. Kunisch, “The Linear Regulator Problem for Parabolic Systems,” SIAM Journal on Control and Optimization, No. 22, Vol. 5, 1984, pp. 684-696. doi:10.1137/0322043
- N. J, Higham, “The Scaling and Squaring Method for the Matrix Exponential,” SIAM Journal on Matrix Analysis and Applications, Vol. 26, No. 4, 2005, pp. 1179-1193. doi:10.1137/04061101X
- A. J. Laub, “A Schur Method for Solving Algebraic Riccati equations,” IEEE Transactions on Automatic Control, Vol. 24, No. 6, 1979, pp. 913-921. doi:10.1109/TAC.1979.1102178
- W. F Arnold and A. J. Laub, “Generalized Eigenproblem Algorithms and Soft-ware for Algebraic Riccati Equations,” Proceedings of the IEEE, vol. 72, No. 12, 1984, pp. 1746-1754. doi:10.1109/PROC.1984.13083

