Journal of Information Security
Vol.4 No.2(2013), Article ID:30064,11 pages DOI:10.4236/jis.2013.42013
A Formal Model of Conformity and Security Testing of Inheritance for Object Oriented Constraint Programming
Laboratory of Research in Computer Science and Telecommunications, Faculty of Science, Ibn Tofail University, Kenitra, Morocco
Email: benlhachmi11@yahoo.fr
Copyright © 2013 Khalid Benlhachmi, Mohammed Benattou. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 1, 2013; revised April 1, 2013; accepted April 9, 2013
Keywords: Conformity Test; Security Test; Constraints Resolution; Formal Specification; Inheritance
ABSTRACT
This paper presents an approach for extending the constraint model defined for conformity testing of a given method of class to its overriding method in subclass using inheritance principle. The first objective of the proposed work is to find the relationship between the test model of an overriding method and its overridden method using the constraint propagation. In this context the approach shows that the test cases developed for testing an original method can be used for testing its overriding method in a subclass and then the number of test cases can be reduced considerably. The second objective is the use of invalid data which do not satisfy the precondition constraint and induce valid output values for introducing a new concept of test called secure testing. The implementation of this approach is based on a random generation of test data and analysis by formal proof.
1. Introduction
The principle of testing is to apply input events to the Implementation under Test (IUT) and to compare the observed output events to the expected results. A set of input events and its corresponding results is generally called test case and can be generated from the IUT specification. The purpose of testing methods is to find the failures that are not detected during system normal operation and to define the relationship between the specifications and implementations of entities under test. Indeed, in object oriented modeling, a formal specification defines operations by collections of equivalence relations and is often used to constrain class and type, to define the constraints on the system states, to describe the preand post-conditions on operations and methods, and to give constraints of navigation in a class diagram. The object oriented constraints (OOC) are specified by formal languages as OCL [1] and JML [2], and are used for generating test data from formal specifications [3]. The proposed test oracles in the industry are satisfied with the conformity test methods, and are carried out by generating test data that conform to the pre-condition constraint. However, a false pre-condition may induce both valid post-condition and invariant at the same time. A correctly implemented testing method should eliminate cases of invalid data which lead to valid results.
In this context, this paper introduces in the first instance an optimizing approach to minimize the test sequences used for testing the conformity of an overriding method in object oriented models. The main idea of this work is the use of a technique that generates test data by exploiting the existing test sequences. Indeed, it is important to reuse the test result of overridden methods for testing the conformity of the overriding methods during inheritance operation. That is why our approach specifies all cases of conformity of an overriding method by using data extracted from conformity testing of the original methods. The second contribution of our approach is the definition of a security testing based on the generation of invalid input data which induce valid output values. Indeed, in this paper we show how we can use the valid data extracted from the pre-condition constraint to test the conformity of an overriding method, and how the data which does not satisfy the precondition can be used to test the security of similar methods. Our test oracle enables to detect anomalies in invalid inputs that imply valid results.
The work presented in this paper allows to extend the constraint model defined in [4] for modeling the specification of an overriding method in subclass using inheritance principle. This work is based on our model of similarity concept [5,6] for testing the conformity and the security of overriding methods from test results of the original methods. The main objective is to reduce the number of test cases by using the test result developed in parent classes, and to integrate the invalid data in test process. We present firstly, the relationship between the test model of overridden and overriding methods, and we show how to use the constraint model for extracting the possible cases of test values. Secondly, we show how it is possible to exploit the invalid data that do not satisfy the precondition constraint and induce valid post-conditions.
This paper is organized as follows: in Section 2 we present related works and similar approaches for generating test data from a formal specification, in Section 3 we describe theoretical aspects of our test process, and we define our test formal model of constraints, in Section 4 we present how the testing formal model can be used to generate data for testing the conformity of overriding methods during inheritance operation, in Section 5 we present our approach of security testing that strengthens the conformity testing, and we show how the security testing of an overriding method can be deduced from its overridden method in parent class. Finally, in Section 6 we describe our approach with an example of conformity and security testing for an object oriented model.
2. Related Works
Most works have studied the problem of relating types and subtypes with behavioral specification in an object oriented paradigm. These proposed works show how the contracts are inherited during method overriding and how the testing process can use the formal specification. In [4], we have presented the definition of a formal model of constraint, illustrating the relationship between pre-conditions, post-conditions and invariants of methods, and we have formalized a generic constraint of a given individual method of class that contains all constraints into a single logical predicate. The given model translates algebraically the contract between the user and the called method.
In [5], we have developed a basic model for the concept of methods similarity, the test is based only on a random generation of input data. In [6], we have generalized the basic model of similarity using analysis of partition and formal proof. In [7], the authors propose a randomly generation of test data from a JML specification of class objects. They classify the methods and constructors according to their signature (basic, extended constructors, mutator, and observer) and for each type of individual method of class, a generation of test data is proposed. In [8], the paper describes specially the features for specifying methods, related to inheritance specification; it shows how the specification of inheritance in JML forces behavioral sub-typing.
The work presented in [9] shows how to enforce contracts if components are manufactured from class and interface hierarchies in the context of Java. It also overcomes the problems related to adding behavioral contracts to Object Oriented Languages, in particular, the contracts on overriding methods that are improperly synthesized from the original contracts of programmer in all of the existing contract monitoring systems. The work is based on the notion of behavioral sub-typing; it demonstrates how to integrate contracts properly, according to the notion of behavioral sub-typing into a contract monitoring tool for java. In [10], the authors treat the problem of types and subtypes with behavioral specifications in object oriented world. They present a way of specification types that makes it convenient to define the subtype relation. They also define a new notion of the subtype relation based on the semantic properties of the subtype and super-type. In [11], they examine various notions of behavioral sub-typing proposed in the literature for objects in component-based systems, where reasoning about the events that a component can raise is important.
All the proposed works concerning the generation of test data from formal specification or to test the conformity of a given method implementation, use only the constraint propagation from super to subclass related to subtype principle and do not exploit the test results of the original method. As an example, several test oracles used in industry as JML compiler can generate the conformity test of an overriding method even if its original method in the parent class does not conform to its specification. Our approach shows that this type of test is unnecessary and can be removed, and presents how we can reduce the test cases by using the test values developed for testing the original methods in a parent class. The main difference between our work and other related works is the definition of the security testing. Indeed, the test methods have focused only on valid inputs satisfying the precondition, and do not integrate the invalid data in test process. Our approach shows how we can use the valid and invalid data extracting from the pre-condition to test the conformity and the security of overridden and overriding methods.
3. Formal Model of Constraint
This section presents a formal model of the generalized constraint defined in [4] which provides a way for modeling the specification of an overriding method by inheritance from a super-class. Indeed, we establish a series of theoretical concepts in order to create a solid basis for testing the conformity of overriding methods in subclasses using the test result of the original methods.
3.1. Constraint Propagation in Inheritance
In [4] we have presented the definition of a formal model of constraint, illustrating the relationship between the pre-condition P, the post-condition Q of a method m and the invariant Inv of the class C: this constraint H is a logical property of the pair (x,o) (x is the vector of parameters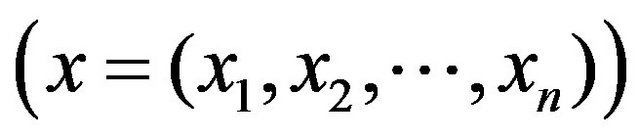 and o is the receiver object) such that:
and o is the receiver object) such that:

where Ic is the set of instances of the class C and E the set of input vectors of m.
Indeed, the invocation of a method m is generally done by reference to an object o and consequently, m is identified by the couple (x,o). The logical implication in the proposed formula means that: each call of method with (x,o) satisfying the precondition P and the invariant before the call, (x,o) must necessarily satisfy the post-condition Q and the invariant Inv after the call. In the context of this work, we assume that the object which invokes the method under test is valid (satisfying the invariant of its class), thus, the objects used at the input of the method under test are generated from a valid constructor. This justifies the absence of predicate Inv of the object o before the call to m in the formula H (Figure 1).
The purpose of this paragraph is to establish a series of theoretical rules in order to evolve the constraint H of a method m of a super-class during the operation of inheritance. We consider a method m of a class C2 which inherits from the class C1 such that m overrides a method of C1. The original method and its overriding method in the subclass C2 will be denoted respectively by m(1), m(2). (P(1),Q(1)) denote respectively the pre-condition, the post-condition of the method m(1), and Inv(1) the invariant of C1; and 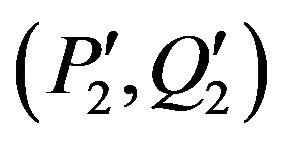 denote respectively the specific pre-condition, post-condition of the overriding method m(2), and
denote respectively the specific pre-condition, post-condition of the overriding method m(2), and ![]() the specific invariant of the class C2. (P(2), Q(2)) denote respectively the pre-condition, the postcondition of the method m(2), and Inv(2) the invariant of C2 (Figure 2).
the specific invariant of the class C2. (P(2), Q(2)) denote respectively the pre-condition, the postcondition of the method m(2), and Inv(2) the invariant of C2 (Figure 2).
The results of this paragraph are based on the works of Liskov, Wing [12] and Meyer [13] who have studied the problem relating to types and subtypes with behavioral

Figure 1. Specification of a method m.
specification in an object oriented (OO) paradigm. Indeed, a derived class obeys the Liskov Substitution Principle (LSP) if for each overriding method m(2), the pre-condition P(2) is weaker than the pre-condition P(1) of the overridden method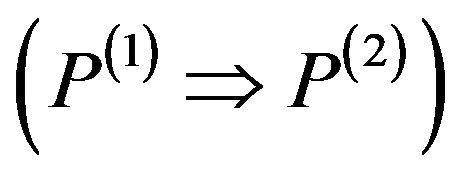 , the post-condition Q(2) is stronger than the post-condition Q(1) of the overridden method
, the post-condition Q(2) is stronger than the post-condition Q(1) of the overridden method , and the class invariant Inv(2) of the subclass C2 must be equal to or stronger than the class invariant Inv(1) of the C1
, and the class invariant Inv(2) of the subclass C2 must be equal to or stronger than the class invariant Inv(1) of the C1 .
.
As a result of LSP:
The pre-condition P(2) of m(2) is the disjunction of P(1) and the specific pre-condition  of m(2) (Figure 2):
of m(2) (Figure 2):
 (1)
(1)
The post-condition Q(2) of m(2) is the conjunction of the post-condition Q(1) of m(1) and the specific post-condition  of m(2) (Figure 2):
of m(2) (Figure 2):
 (2)
(2)
The invariant Inv(2) of the class C2 is the conjunction of the invariant Inv(1) of C1 and the specific invariant ![]() of C2 (Figure 2):
of C2 (Figure 2):
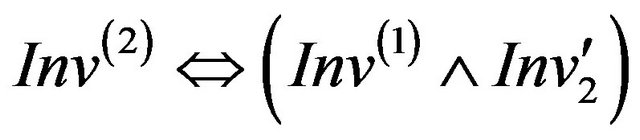 (3)
(3)
Based on the definition of the generalized constraint, we have:
The constraint of m(1):
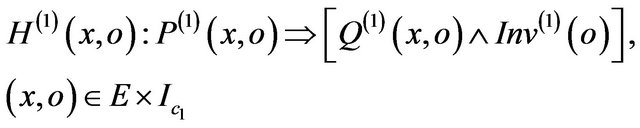
The constraint of m(2):
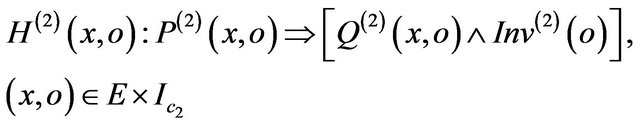
Using (1), (2), (3) the constraint of m(2) will have the following form:

In our approach, the specification 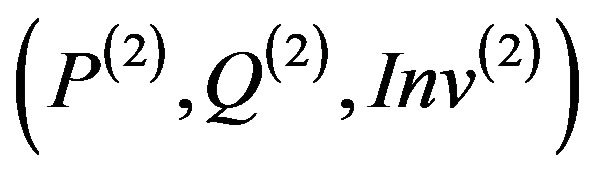 of m(2) is constituted by :
of m(2) is constituted by :
Two inputs: the Basic Input  and the Specific Input
and the Specific Input 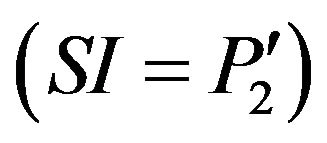 of m(2).
of m(2).
Two outputs: Basic Output  and the Specific Output
and the Specific Output 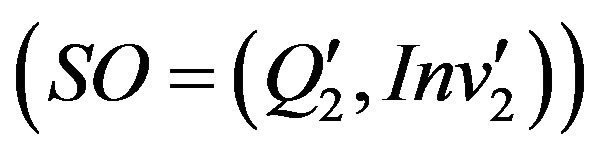 of m(2).
of m(2).
This induces 4 possible combinations of I-O: (BI,BO), (BI,SO), (SI,BO), (SI,SO).
3.2. Constraint Model of Overriding Methods
The aim of this paragraph is to construct a formal model of an overriding method by generalizing the constraint

Figure 2. Constraints of m(1) and m(2).
model of the original methods. In achieving this goal, we should define a specific constraint of inheritance and also study the compatibility between the overriding methods and original methods in the parent class.
In this sense, we had proposed in [5,6] the definition of similarity concept for assuring if the overriding method m(2) has the same behavior as its original version m(1) in the super-class relatively to their common specification . Indeed, the implementation in the subclass must override the implementation in the super class by providing a method m(2) that is similar to m(1). We propose firstly the definition of a constraint H(SI,SO) allowing a partial view of the overriding method m(2) in the class C2. Secondly, we determine the relationship between the constraints H(2), H(1) and H(SI,SO).
. Indeed, the implementation in the subclass must override the implementation in the super class by providing a method m(2) that is similar to m(1). We propose firstly the definition of a constraint H(SI,SO) allowing a partial view of the overriding method m(2) in the class C2. Secondly, we determine the relationship between the constraints H(2), H(1) and H(SI,SO).
The constraint H(SI,SO) specifies the logical relationship between the input specific predicate 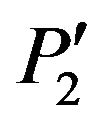 of m(2) and the output predicates
of m(2) and the output predicates 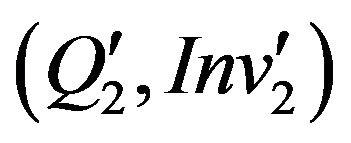 specific to m(2):
specific to m(2):
Definition 1: (Constraint H(SI,SO))
We define the constraint H(SI,SO) of an overriding method m(2) of a sub-class C2 as a logical property of the pair 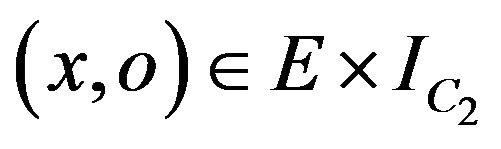 such that:
such that:
![]()
where 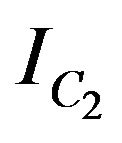 is the set of instances of C2, and E is the set of parameters vector of m(2).
is the set of instances of C2, and E is the set of parameters vector of m(2).
The logical implication in the proposed formula means that: each call of method with (x,o) satisfying the specific precondition 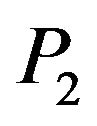 before the call, (x,o) must necessarily satisfy the specific post-condition
before the call, (x,o) must necessarily satisfy the specific post-condition  and the specific invariant
and the specific invariant ![]() after the call.
after the call.
In the same way, we put:

And
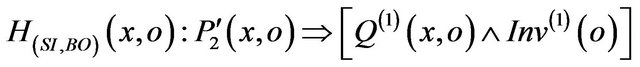
The relationship between H(1) and H(2) for the two similar methods m(1) and m(2) in classes C1 and C2 is shown in the following theorem:
Theorem 1:
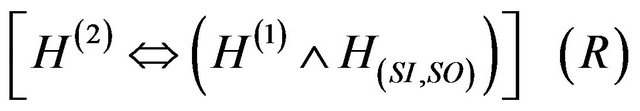
Proof: Using the following result:
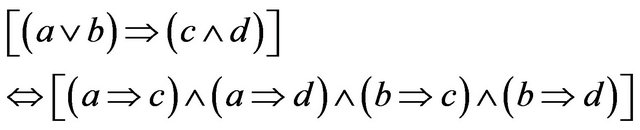
We have:
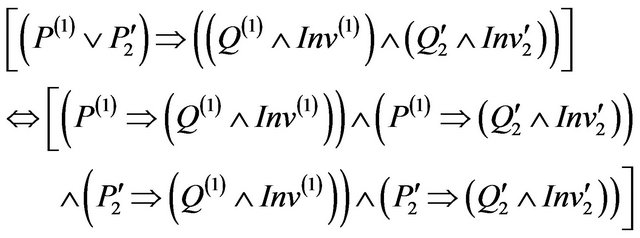
Therefore, we have the following result:

In principle, the method m(2) is not intended to provide the services (SI,BO) and (BI,SO) however m(2) must guarantee the services (BI,BO) (Figure 3) and (SI,SO) (Figure 4). Consequently, we put:  and
and .
.
Finally, (R) is equivalent to
 .
.
The constraints H(1), H(SI,SO), and the relation (R) form the theoretical basis that will be used to test the conformity of overriding methods in subclasses from the test result of their original methods in the parent classes.
4. Conformity Testing
The formal model of test proposed in [4] defines the no-

Figure 3. Constraint BI-BO of an overriding method.
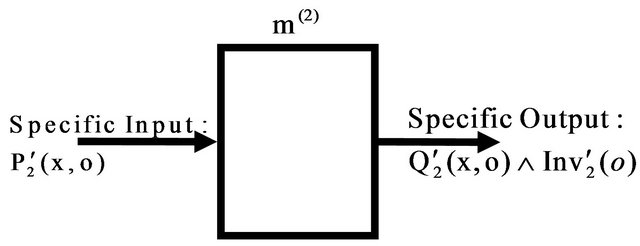
Figure 4. Constraint SI-SO of an overriding method.
tion of method validity in a basic class and constitutes a way to generate test data for conformity. In a conformity test, the input data must satisfy the precondition of the method under test. In this context, we are particularly interested in valid input values (i.e. the pairs (x,o) that satisfy the precondition P). The conformity test for a method means that if a pre-condition is satisfied at the input, the post-condition and the invariant must be satisfied at the output. The purpose of this section is to generalize the model of [4-6] in order to test the conformity of an overriding method m(2) in a derived class by using the elements of conformity test of its original method m(1) in the super-class.
In [4], we have tested the conformity of methods in a basic class without taking into account the inheritance relationship: the model of test generates random data at the input of a method using elements of the valid domain which satisfy the precondition of the method under test. This test stops when the constraint H becomes False 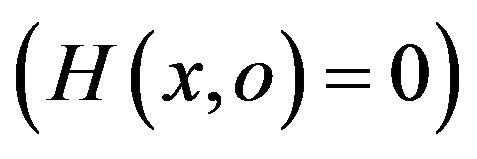 or when the maximum threshold of the test is reached with H satisfied.
or when the maximum threshold of the test is reached with H satisfied.
Definition 2: (Valid method)
A method m of class C is valid or conforms to its specification if for each , the constraint H is satisfied:
, the constraint H is satisfied: 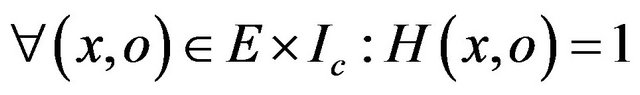
In other words, for a valid method: : If (x,o) satisfies the precondition P then this (x,o) must satisfy the post-condition Q and the invariant Inv.
: If (x,o) satisfies the precondition P then this (x,o) must satisfy the post-condition Q and the invariant Inv.
The conformity test of m(2) requires the following steps:
• Step 1: a conformity test of a basic constructor of class C2. This step is necessary for using valid objects at the input of the method under test.
• Step 2: a similarity test of m(1) and m(2) relatively to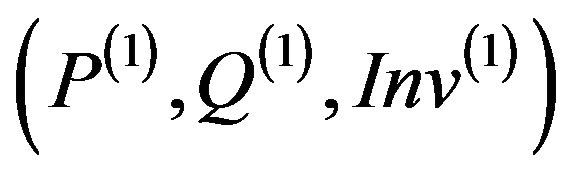 .
.
We assume that the test of step 2 showed that m(1) and m(2) are similar.
The conformity test process of the overriding method m(2) relatively to H(2) is based on the test result of m(1) relatively to H(1) and the test result of m(2) relatively to H(SI,SO) (Theorem1).
The conformity test of m(1) induces two cases: m(1) conforms to its specification or m(1) is not in conformity with its specification:
• Case 1: The method m(1) is not in conformity with its specification We have the following result:
Theorem 2:
If the overridden method m(1) in parent class C1 is not in conformity with its specification 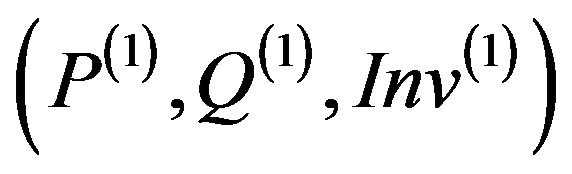 then any similar method m(2) in a subclass is not in conformity with its specification
then any similar method m(2) in a subclass is not in conformity with its specification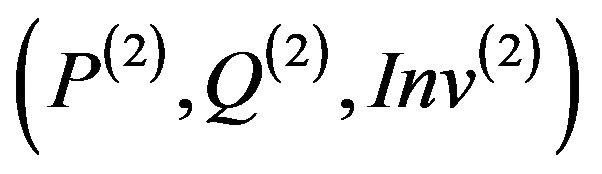 .
.
Proof:
We assume that the method m(1) is not in conformity with its specification. This means (Def. 2) that:
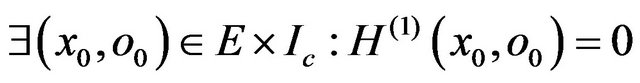
The object o0 is an instance of the class C1. We consider an object 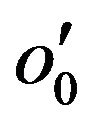 of the subclass C2 that has the same values as the object o0 for attributes of C1 And therefore, the object
of the subclass C2 that has the same values as the object o0 for attributes of C1 And therefore, the object  has the same behavior as o0 in a context of C1 and consequently:
has the same behavior as o0 in a context of C1 and consequently:
![]()
We apply the relationship (R) (Theorem 1) on the pair  of the domain
of the domain :
:
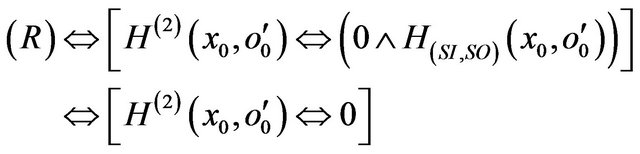
This means: ![]()
This shows (Def. 2) that the method m(2) is not in conformity with its specification.
• Case 2: The method m(1) conforms to its specification In this case, we have (Def. 2):
![]()
Using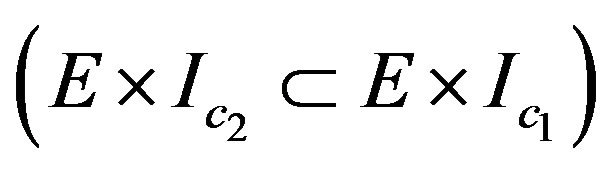 , we have:
, we have:
![]()
The relationships (R) in theorem1implies:
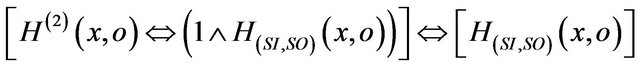
Therefore, we must to test m(2) relatively to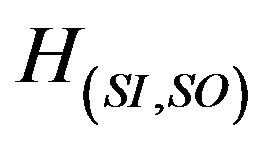 :
:
• m(2) is not in conformity with H(SI,SO)
We have in this case, the following result:
Theorem 3:
If the overriding method m(2) of the subclass C2 is not in conformity relatively to its specific constraints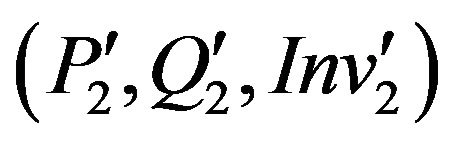 , then the method m(2) is not in conformity with its global specification
, then the method m(2) is not in conformity with its global specification .
.
Proof:
We assume that the method m(2) does not satisfy its specific constraint H(SI,SO):
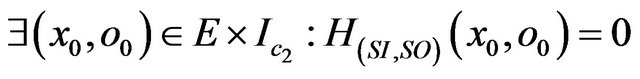
Applying the relationship (R):
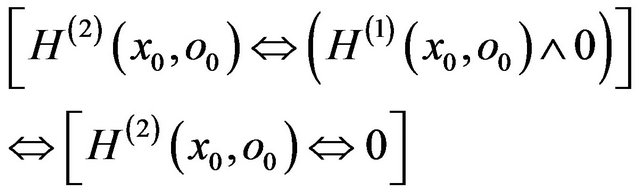
and consequently: ![]()
This induces that m(2) is not in conformity with its global specification (Def. 2) .
• m(2) conforms to its specific constraint H(SI,SO)
We have in this case, the following result:
Theorem 4:
If the overridden method m(1) of the class C1 conforms to its specification, and its similar method m(2) in the subclass C2 conforms to the specific constraint H(SI,SO), we deduce that the overriding method m(2) conforms to its global specification.
Proof:
In this case, we have:
![]() and
and 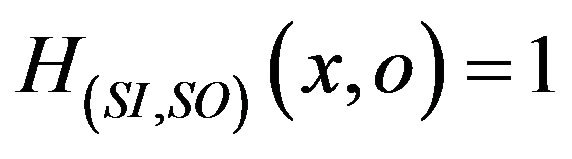
The relationships (R) implies: 
This means: ![]()
We deduce that the overriding method m(2) conforms to its global specification (Def. 2).
5. Security Testing
5.1. Formal Model of Security Testing
The realized tests for conformity consider that the input data satisfy the precondition. However, a false pre-condition may induce both a post-condition and an invariant which are valid. A correctly testing of implementation of a method should reject cases of invalid data which provide valid results. Most of test oracles do not integrate the invalid data in test process. This section presents a complementary test aimed to study the invalid inputs of a method that conforms to its specification. Indeed, an anomaly difficult to be detected arises when a couple (x,o) does not satisfy the pre-condition P is accepted and induces both a post-condition Q and invariant Inv that are valid at the output. Our approach allows resolving these anomalies by the introduction of a complementary test for each method m that conforms to its specification. On the theoretical level, we are looking for strengthening the current constraint H in order to integrate this type of test.
Consider a method m of class C such that: o the receiver object and x the vector of parameters.
Definition 3: (Secure method)
The method m is secure relatively to its specification if it satisfies the following conditions:
• It conforms to its specification.
• For each invalid couple (x,o) of input (does not satisfy the pre-condition: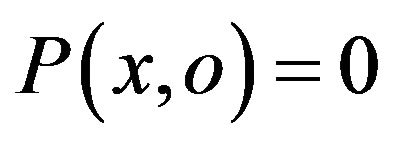 ), the post-condition Q and the invariant Inv should not be both valid in output:
), the post-condition Q and the invariant Inv should not be both valid in output: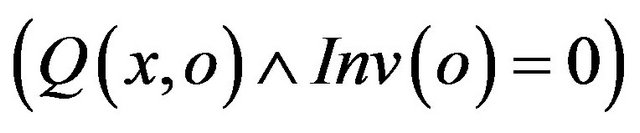 .
.
As is shown in Table 1, the constraint H defined above for conformity test takes in the security test the following form:

We note:

Table 1. Truth cases of H and Hsecurity.
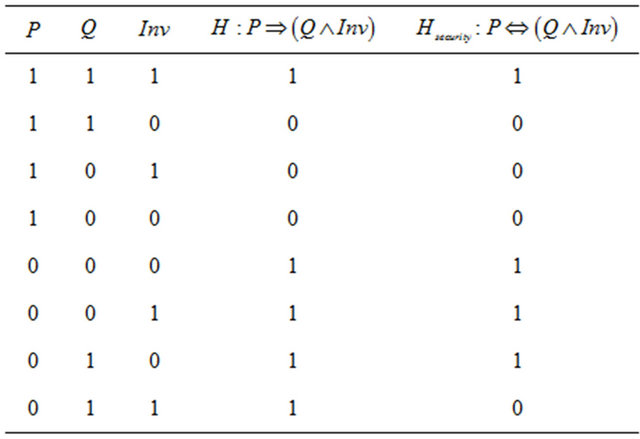
In this test, we assume that with an invalid input, we can expect only an invalid result: any valid result coming from an invalid input indicates the presence of a security problem into the method implementation.
Theorem 5: The method m is secure relatively to its specification, if: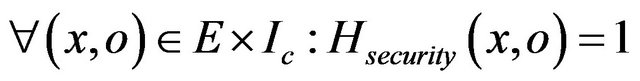 .
.
5.2. Algorithm of Security Testing
The main aim of security testing algorithm is the use of the proposed security testing model for checking if the method under test is secure relatively to its specification. We assume that the method under test is conforming to its specification. The test data generation requires that the input values generated must not satisfy the pre-condition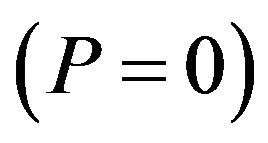 . The execution of each security test algorithm stops when the constraint Hsecurity becomes false
. The execution of each security test algorithm stops when the constraint Hsecurity becomes false 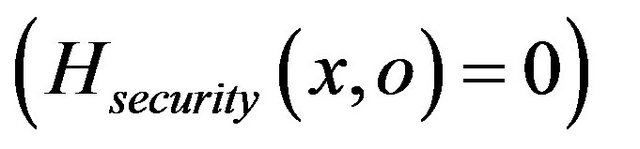 or when we reach the threshold of test with
or when we reach the threshold of test with . In the Figure 5, the constant N is an input value and (A21, A22, A23, A24) is the partition of the invalid input domain of the method m:
. In the Figure 5, the constant N is an input value and (A21, A22, A23, A24) is the partition of the invalid input domain of the method m:
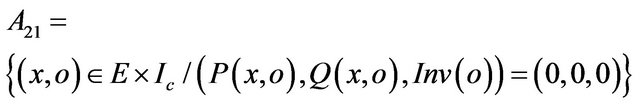

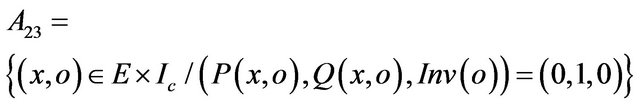

5.3. Security Testing in Inheritance
The purpose of this paragraph is to test the security of an overriding method m(2) relatively to its global specification 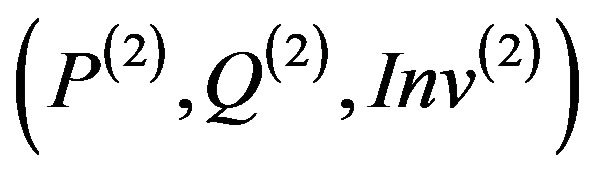 in a derived class C2 using the
in a derived class C2 using the

Figure 5. Security test algorithm of the method m.
elements of security test of its original method m(1) in the super-class C1.
Definition 4: (Security of m(2) relatively to 
An overriding method m(2) is secure relatively to its inherited specification  if:
if:
• m(2) conforms to its inherited specification  .
.
• For each couple (x,o) in the invalid input domain of m(2) , the post-condition Q(1) and the invariant Inv(1) should not be both valid in output of m(2)
, the post-condition Q(1) and the invariant Inv(1) should not be both valid in output of m(2)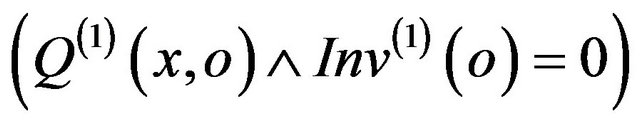 .
.
Definition 5: (Security of an overriding method m(2) relatively to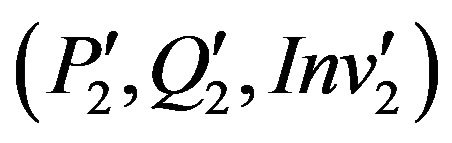 ).
).
An overriding method m(2) is secure relatively to its own specification 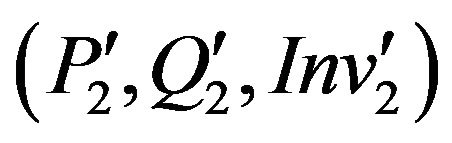 if:
if:
• m(2) conforms to its own specification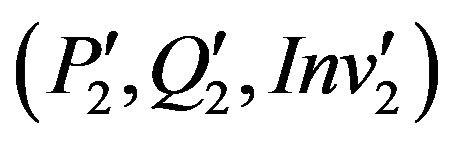 .
.
• For each couple (x,o) in the invalid input domain of m(2)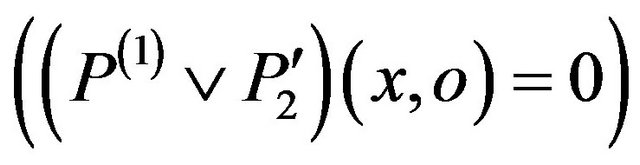 , the post-condition
, the post-condition 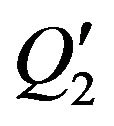 and the invariant
and the invariant ![]() should not be both valid in output of m(2)
should not be both valid in output of m(2) .
.
Definition 6: (Security of an overriding method m(2) relatively to its global specification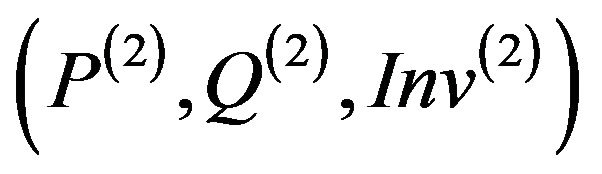 )
)
An overriding method m(2) is secure relatively to its global specification  if and only if:
if and only if:
• m(2) is secure relatively to its inherited specification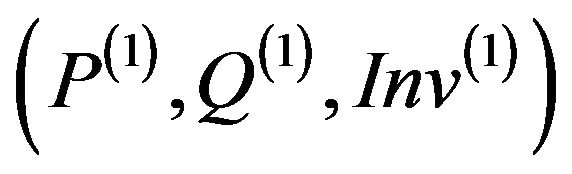 .
.
• m(2) is secure relatively to its own specification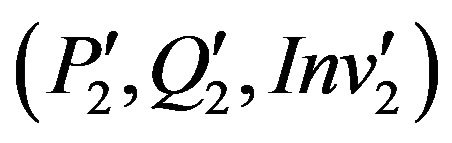 .
.
Theorem 6:
An overriding method m(2) is secure relatively to its global specification 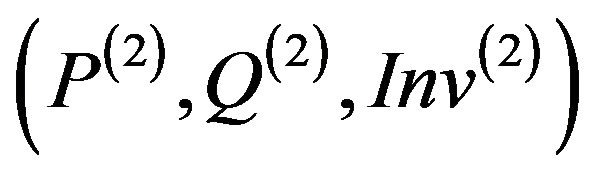 if:
if:
• m(2) conforms relatively to its global specification .
.
• For each invalid couple (x,o) of input (does not satisfy the pre-condition , the post-condition Q(2) and the invariant Inv(2) should not be both valid in output of m(2)
, the post-condition Q(2) and the invariant Inv(2) should not be both valid in output of m(2) .
.
Theorem 7:
An overriding method m(2) (that conforms to its global specification) is not secure relatively to this specification if
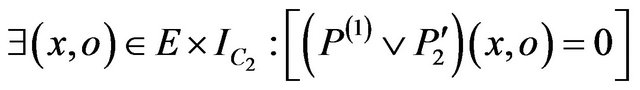
in input of m(2) and
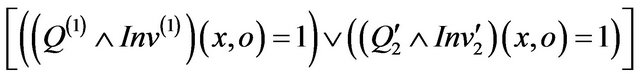
in output of m(2).
The security test of m(2) relatively to its global specification  is performed only if the conformity test of m(2) relatively to
is performed only if the conformity test of m(2) relatively to  is validated. We consider that m(1) and m(2) are in conformity with their specifications, and we assume that the security test of m(2) starts when the security testing of m(1) is completed. Indeed, the security test of m(1) induces two cases: m(1) is secure relatively to its specification or m(1) is not secure relatively to its specification:
is validated. We consider that m(1) and m(2) are in conformity with their specifications, and we assume that the security test of m(2) starts when the security testing of m(1) is completed. Indeed, the security test of m(1) induces two cases: m(1) is secure relatively to its specification or m(1) is not secure relatively to its specification:
· Case 1: m(1) is not secure relatively to its specification.
We assume that the method m(1) is not secure relatively to its specification. This means (Def. 3 and Th. 5) that:
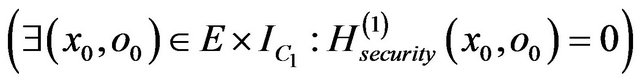
The object o0 is an instance of the class C1. We consider an object 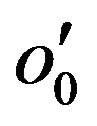 of the subclass C2 that has the same values as the object o0 for attributes of C1 and therefore, the object
of the subclass C2 that has the same values as the object o0 for attributes of C1 and therefore, the object  has the same behavior as o0 in a context of C1 and consequently:
has the same behavior as o0 in a context of C1 and consequently:

i.e.

m(1) and m(2) are similar, then we have:
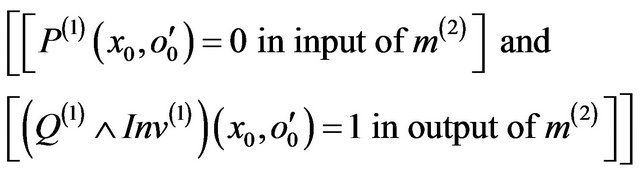
We have two cases:  or
or 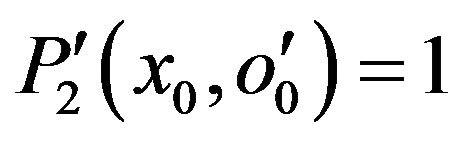
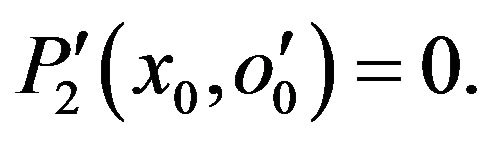
In this case, we have:
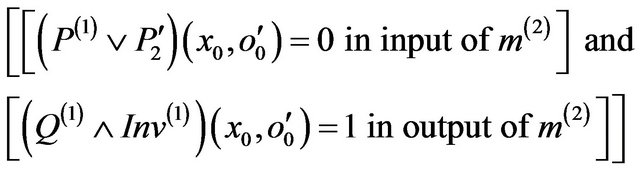
Consequently the method m(2) is not secure relatively to 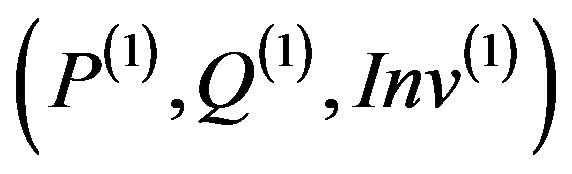 (Def. 4).
(Def. 4).
Finally, this shows (Th. 7) that the method m(2) is not secure relatively to its global specification  .
.
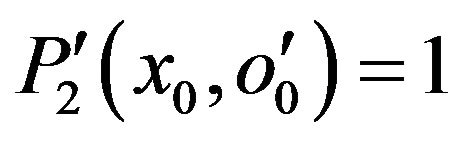
In this case, we have: 
Consequently the couple 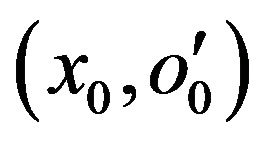 is in the valid input domain: the security of m(2) cannot be deduced from the security test of m(1) (Figure 6).
is in the valid input domain: the security of m(2) cannot be deduced from the security test of m(1) (Figure 6).
· Case 2: m(1) is secure relatively to its specification.
In this case, we must test the method m(2) relatively to its own specification  (Figure 6).
(Figure 6).
6. Evaluation
We evaluate the correctness of our approach by implementing the algorithm of conformity and security testing for inheritance. We consider for example of conformity and security testing the methods withdraw(1) and withdraw(2) of the class Account1 and Account2 (Figure 7).
The constraints H(1) and H(2) of withdraw(1) and withdraw(2) in an algebraic specification are shown in the Figure 8 (x = x1, o(a) and o(b) are respectively the object o after and before the call of the method):
• Conformity testing for withdraw(2) and withdraw(1)
We test firstly the similarity of withdraw(2) and withdraw(1) on the common valid domain CVD
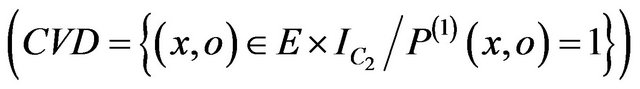 : for each (x ,o) that satisfy the common precondition of withdraw(1) and withdraw(2)
: for each (x ,o) that satisfy the common precondition of withdraw(1) and withdraw(2)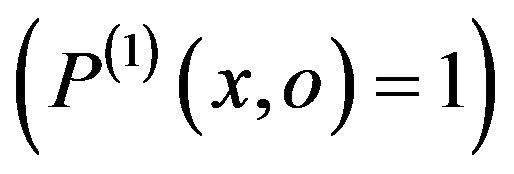 , the condition of the block if {…} (method withdraw(2) in Figure 7) is not satisfied, and thus the block if {…} is not executed, this means that the method withdraw(2) does exactly the same thing as
, the condition of the block if {…} (method withdraw(2) in Figure 7) is not satisfied, and thus the block if {…} is not executed, this means that the method withdraw(2) does exactly the same thing as

Figure 6. Security test cases for an overriding method.

Figure 7. Account1 and Account2 classes.
the method withdraw(1) (Figure 7). As a result thereof, withdraw(2) and withdraw(1) are similar on the valid domain CVD.
The second test concerns the conformity testing of withdraw(2) that is based on the conformity testing of withdraw(1):
• Conformity Testing for withdraw (1)
In order to test the conformity of withdraw (1) in class Account1, we generate randomly x1 and the balance values in the interval (‒200,200) with N =100 (Table 2):
The test result shows that for 100 iterations the constraint H(1) is always true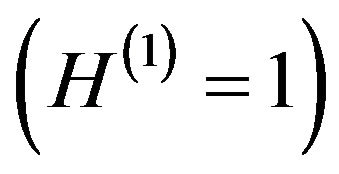 , we can deduce that the withdraw(1) method is valid (Table 2). In this case it is necessary to test the method withdraw(2) relatively to its own constraint H(SI,SO):
, we can deduce that the withdraw(1) method is valid (Table 2). In this case it is necessary to test the method withdraw(2) relatively to its own constraint H(SI,SO):
• Conformity testing for withdraw(2) relatively to H(SI,SO)
In order to test the method withdraw(2) relatively to the constraint H(SI,SO), we use an analysis with proof. The testing by proof of the method withdraw(2) relatively to the constraint H(SI,SO) is used to strengthen the randomly testing .Indeed, we must have for satisfying the specific output (SO) :
◦ The specific post-condition 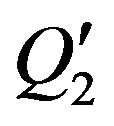 must be satisfied.
must be satisfied.
◦ The specific invariant ![]() must be satisfied.
must be satisfied.
The constraint  is always satisfied (Figures 7 and 8), however we must proof that
is always satisfied (Figures 7 and 8), however we must proof that ![]() is satisfied.
is satisfied.
For each created object o0 ,we have : (0 ≤ InterestRate0 ≤ 0.3) where InterestRate0 is the initial value assigned to InterestRate when creating the object o0, and InterestRate(n) is the value of InterestRate after n operations of type withdraw(2) in an execution sequence.
We have:
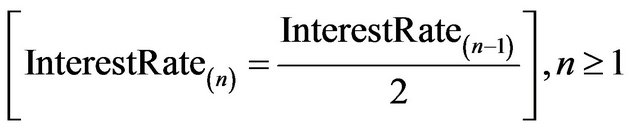
Table 2. Result of a conformity test of withdraw(1)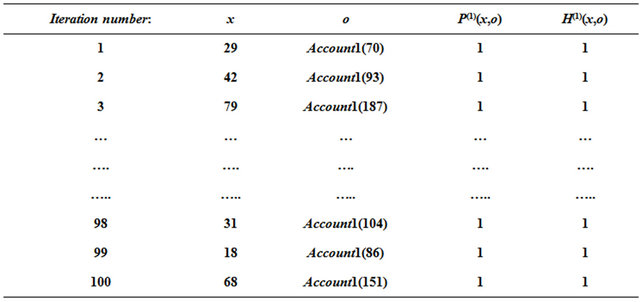
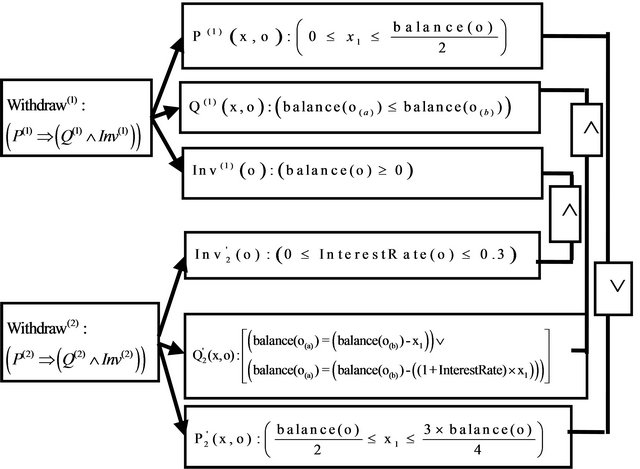
Figure 8. Constraints of withdraw(1) and withdraw(2).
where n is number of withdrawals (Figure 7).
The geometric series proposed is written in the general case as follows:

We deduce that:

And consequently, the specific invariant is always satisfied (Figure 8). This leads to the conclusion that the method withdraw(2) is in conformity to H(SI,SO), and we can deduce that withdraw(2) is in conformity with its global specification.
• Security testing for withdraw(2) and withdraw(1)
For security testing, we test firstly the similarity of withdraw methods on the common invalid domain CID
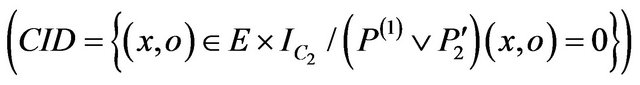
For this we generate randomly x1 and the balance values in the interval (‒200,200) with the threshold limit N =100 (Table 3).
The test result shows that for 100 iterations the size of the similarity set Sim is exactly the threshold limit of the test. We can conclude that the methods withdraw(2) and withdraw(1) are similar on the domain CID relatively to
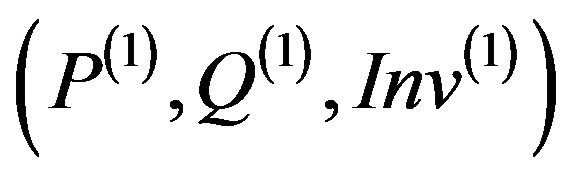 (Table 3).
(Table 3).
In the last paragraph, we have showed that withdraw(2) and withdraw(1) are in conformity with their specifications and are similar on the common invalid domain. For testing the security of the overriding method withdraw(2), we must testing the security of the overridden method withdraw(1) (Figure 6):
• Security Testing for withdraw(1) relatively to 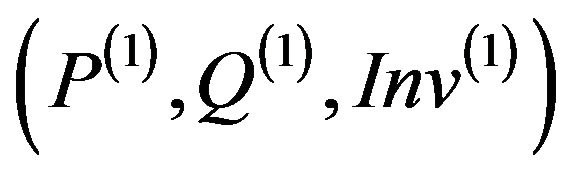
We generate in the Table 4 the security test cases for the overridden method withdraw(1) relatively to :
:
For the first four iterations, we have:
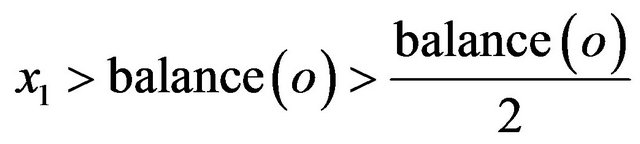 i.e.
i.e. 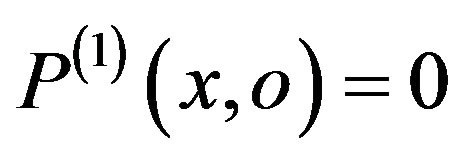 and it induces to a false invariant
and it induces to a false invariant 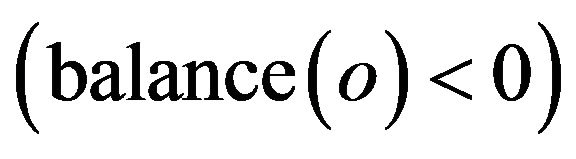 at the output, i.e.
at the output, i.e. . In the iteration 5, we have for
. In the iteration 5, we have for
 :
:
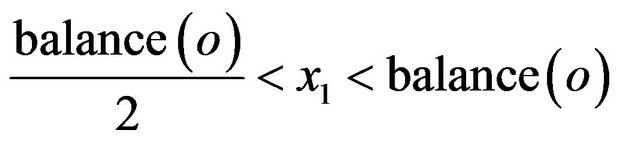
Table 3. Similarity test of the withdraw methods on CID.
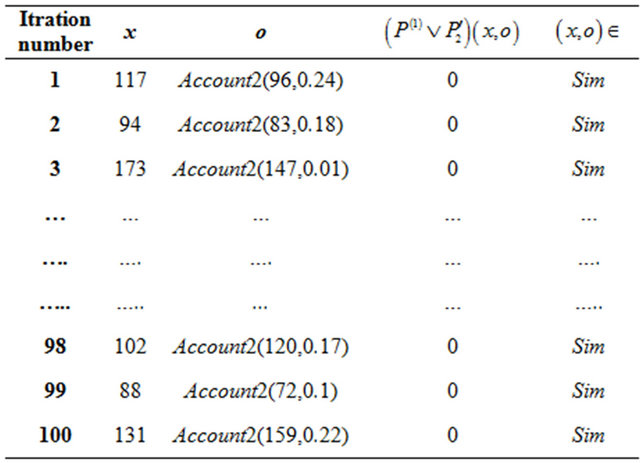
Table 4. Security test of withdraw(1)/(P(1), Q(1),Inv(1)).

i.e. , and this induces
, and this induces  and
and , i.e.
, i.e.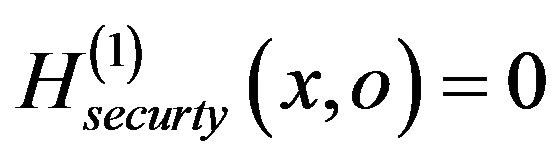 . Indeed, our implementation cannot reject this situation and conesquently the overridden method withdraw(1) under test which is conforming to its specification, is considered not secure relatively to the same specification.
. Indeed, our implementation cannot reject this situation and conesquently the overridden method withdraw(1) under test which is conforming to its specification, is considered not secure relatively to the same specification.
• Security Testing for withdraw(2) relatively to 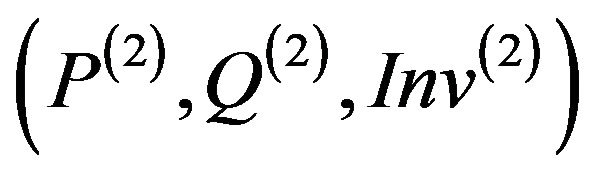
According to the Figure 6, we have for (x,o) = 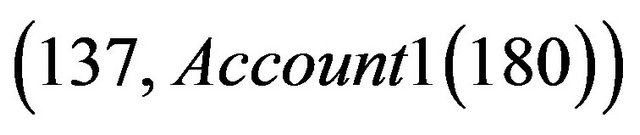 the method withdraw(1) is not secure, we consider for example the object o’ of the class Account2 that has the same balance value
the method withdraw(1) is not secure, we consider for example the object o’ of the class Account2 that has the same balance value
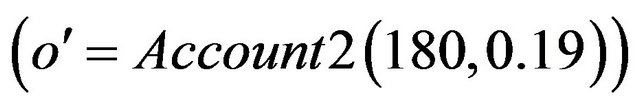 and we must determinate the truth value of
and we must determinate the truth value of (Figure 6).
(Figure 6).
We have:
i.e. 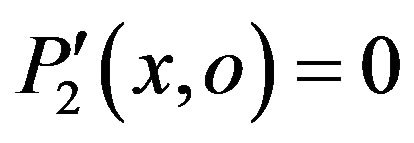 (Figure 8).
(Figure 8).
Finally, we can deduce that withdraw(2) is not secure relatively to 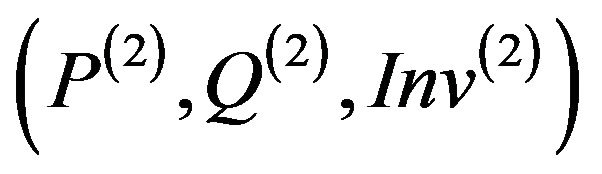 (Figure 6).
(Figure 6).
7. Conclusions
This paper introduces an approach to reduce the test sequences used for testing the conformity of an overriding method during inheritance operation in object oriented models. The key idea of this work is the use of a technique that generates test data by exploiting the existing test sequences. Indeed, for the sub-classes methods that have the same behavior as their corresponding methods in a parent class, it is possible to reuse the data extracted from the conformity testing of an overridden method for testing the conformity of its overriding method.
The main contribution of our approach is the definition of a security testing that generates invalid input values not satisfying the precondition constraint. Indeed, the test methods have focused only on valid inputs satisfying the pre-condition, and do not integrate the invalid data in test process. We think that a correctly implemented testing method should eliminate cases of invalid data which lead to valid results. Our approach shows how we can use the valid and invalid data extracted from the pre-condition to test the conformity and security of overridden and overriding methods.
We present firstly the relationship between the test model of overridden methods and overriding methods, and we show how the use of existing test sequences can make the generation of the test data during inheritance less expensive. Secondly, we present our approach of security testing based on data not satisfying the precondition constraint.
REFERENCES
- B. K. Aichernig and P. A. P. Salas, “Test Case Generation by OCL Mutation and Constraint Solving,” Proceedings of the International Conference on Quality Software, Melbourne, September 19-20, 2005, 2005, pp. 64-71.
- F. Bouquet, F. Dadeau, B. Legeard and M. Utting, “Symbolic Animation of JML Specifications,” International Conference on Formal Methods, Vol. 3582, SpringerVerlag, 2005, pp. 75-90.
- M. Benattou, J.-M. Bruel and N. Hameurlain, “Generating Test Data from OCL Specification,” Proceedings of the ECOOP’2002 Work-Shop on Integration and Transformation of UML Models (WITUML’2002), 2002.
- K. Benlhachmi, M. Benattou and J.-L. Lanet, “Génération de Données de Test Sécurisé à Partir d’une Spécification Formelle par Analyse des Partitions et Classification,” Proceedings of the International Conference on Network Architectures and Information Systems Security (SAR-SSI 2011), La Rochelle, 18-21 May 2011, pp. 143-150.
- K. Benlhachmi and M. Benattou, “A Formal Model of Similarity Testing for Inheritance in Object Oriented Software,” Proceedings of the IEEE International Conference (CIST’2012), Fez, 24-26 October 2012, pp. 38-42.
- K. Benlhachmi and M. Benattou, “Similarity Testing by Proof and Analysis of Partition for Object Oriented Specifications,” Journal of Theoretical and Applied Information Technology, Vol. 46, No. 11, 2012, pp. 461-470.
- Y. Cheon and C. E. Rubio-Medrano, “Random Test Data Generation for Java Classes Annotated with JML Specifications,” Proceedings of the 2007 International Conference on Software Engineering Research and Practice, Volume II, 25-28 June 2007, Las Vegas, pp. 385-392.
- G. T. Leavens, “JML’s Rich, Inherited Specification for Behavioral Subtypes,” Iowa State University, Ames, 2006.
- R. B. Findler, M. Latendresse and M. Felleisen, “Behavioral Contracts and Behavioral Subtyping,” Foundations of Software Engineering, Rice University, Houston, 2001.
- B. H. Liskov and J. M. Wing, “A Behavioral Notion of Subtyping,” MIT Laboratory for Computer Science, Carnegie Mellon University, ACM Transactions on Programming Languages and Systems, Vol. 16, No. 6, 1994, pp. 1811-1841.
- G. T. Leavens and K. K. Dhara, “Concepts of Behavioral Subtyping and a Sketch of their Extension to Component-Based Systems,” In: G. T. Leavens and M. Sitaraman, Eds., Foundations of Component-Based Systems, 2000, pp. 113-135.
- B. H. Liskov and J. Wing, “Behavioral Subtyping Using Invariants and Constraints,” Technical Report CMU CS-99-156, School of Computer Science, Carnegie Mellon University, Pittsburgh, 1999.
- B. Meyer, “Object Oriented Software Construction,” Prentice Hall, Upper Saddle River, 1988.

