Materials Sciences and Applications
Vol.06 No.07(2015), Article ID:58031,14 pages
10.4236/msa.2015.67068
First Principles Study of the Structural and Electronic Properties of the ZnO/Cu2O Heterojunction
Mabrouk Zemzemi, Sahbi Alaya
Laboratory of Physics of Materials and Nanomaterials applied to Environment, Faculty of Sciences of Gabes, University of Gabes, Gabes, Tunisia
Email: mzemzemi@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 March 2015; accepted 13 July 2015; published 16 July 2015
ABSTRACT
Many materials have been used in nanostructured devices; the goal of attaining high-efficiency thin-film solar cells in such a way has yet to be achieved. Heterojunctions based on ZnO/Cu2O oxides have recently emerged as promising materials for high-efficiency nanostructured devices. In this work, we are interested in the characterization of the surface and interface through nano- scale modeling based on ab initio (Density Functional Theory (DFT), Local Density Approximation (LDA), Generalized Gradient Approximation (GGA-PBE), and Pseudopotential (PP)). This study aims also to build a supercell containing a ZnO/Cu2O heterojunction and study the structural properties and the discontinuity of the valence band (band offset) from a semiconductor to an- other. We investigate crystal terminations of ZnO (0001) and Cu2O (0001). We calculate the energies of the polar surfaces and the work function in the c-axis for both oxides. We built a zinc oxide layer in the wurtzite structure along the [0001] direction, on which we placed a copper oxide layer in the hexagonal structure (CdI2-type). We choose the method of Van de Walle and Martin to calcu- late the energy offset. This approach fits well with the DFT. Our calculations give us a value that corresponds to other experimental and theoretical values.
Keywords:
Heterojunction, Structure and Electronic Properties, Band Offsets, Surface Energy, Workfunction, Density Functional Theory, Average Potential Method

1. Introduction
Many different photovoltaic technologies are being developed for large-scale solar energy conversion [1] [2] . Photovoltaic devices offer the possibility of low-cost fabrication of large-area solar cells for harvesting energy from sunlight [3] [4] . A promising strategy to install novel concepts incorporates often enabling technologies such as nanotechnology, which aims to modify the active layer to better match the solar spectrum, or to preferentially modify the incoming solar radiation before it impinges on the active layer. Design, growth and characterization of new generation of solar cells are nowadays important research fields [5] [6] . In the recent years, a large amount of experimental and theoretical work focused on heterostructures composed of ultrathin layers designed for new solar energy converters working under a low light intensity. However, the development of new solar cells with improved performances and lower cost requires new approaches based on the use of clean, low cost and non-toxic materials prepared via low energy processes. Simulation methods are used to predict the characteristics of a semiconductor which will operate with an optimum efficiency as a photovoltaic solar energy converter. The existence of such an optimum material results from the interaction between the optical properties of the semiconductor which determine which fraction of the solar spectrum is utilized and its electrical properties which determine the maximum efficiency of conversion into electricity [7] .
Photovoltaic cell requires two semiconductor slabs (n-type and p-type). Zinc oxide (ZnO) attracted researchers’ attention for a long time, owing to its potential applications in many scientific and industrial areas [8] [9] . Ac- tually, its non-toxicity and natural abundance make it an ideal candidate for many industrial manufacturing processes [10] . ZnO belongs to the family of the transparent conductive oxides (TCO). It is generally an n-type semiconductor, with a wide band gap of 3.4 eV and an exciton binding energy of 60 meV. These features make ZnO, like GaN, a candidate for applications to blue and ultra-violet optical devices [11] . Cuprous oxide (Cu2O) is also a potential material for the fabrication of low cost solar cells [12] [13] . The first Cu2O-based solar cell was manufactured at the end of 1920. However, at that time, and until the first space explorations, the energy production from the sunlight by the photovoltaic effect was just a curiosity. Cu2O is a p-type semiconductor with a direct band gap of about 2 eV, which is suitable for photovoltaic conversion.
The ZnO/Cu2O heterojunction has been fabricated and studied for a long time [14] . Thanks to the low cost and non-toxic character of its constituents, this heterojunction has recently attracted a renewed interest [15] -[20] . Its efficiency is still quite small (2%), but better performances can be expected by improving the crystalline order and the interface features. Considerable attention is devoted to improving the electronic properties at inter- faces and to growing the heterostructure along crystallographic directions that provide stability and increase efficiency. ZnO has a hexagonal (wurtzite) structure, while Cu2O is cubic (cuprite). An epitaxial growth of (111)- oriented Cu2O film on the (0001) surface of ZnO is thus possible as it has been reported in several papers [21] [22] . Nevertheless, studies of Cu2O under pressure [23] [24] show that this crystal undergoes a transition to a hexagonal phase, which is a polytype of the CdI2 structure. This suggests that a growth of Cu2O films according to the CdI2 structure on a ZnO substrate is also possible. This kind of growth would have the advantage of giving superlattices preserving the stoichiometry. In the present work, we will investigate this kind of growth.
Surface and interface physics has in recent decades become an ever more important sub-discipline within the physics of condensed matter. Many phenomena and experimental techniques cannot be treated without a pro- found knowledge of surface and interface effects [25] . A solid interface is defined as a small number of atomic layers that separate two solids in intimate contact with one another, where the properties differ significantly from those of the bulk material it separates. Surface and interface energies in the heterojunction are decisive parameters for the thin film microstructure in the growth process. For ZnO and Cu2O, surface energy represents a non-negligible contribution for the overall energetic balance [26] . Hence, it is important to study this property and determine its contribution. Particular attention is given to the polar surfaces because ZnO and Cu2O possess preferred directions [27] . The crystal’s c-axis orientation of ZnO and Cu2O is polar, and has a positively charged Zn- or Cu-terminated (0001) surface and negatively charged O-terminated (000-1) surface [28] -[30] . Experimental studies have been performed to characterize the polar surfaces of ZnO [31] and Cu2O [32] . Many theoretical calculations have been used to verify and confirm the preferred polar surfaces [33] [34] . This study is motivated by the fact that bulk and surface properties are intimately linked and to get a good understanding of interface. ZnO and Cu2O bulk, polar surfaces, and interactions among surfaces forming the heterojunction have to be considered.
Many important properties of semiconductors are not solely determined by the band gap. For instance, the relative band bending near two different semiconductors and the corresponding band offsets are of fundamental interest in solid state physics, and are indispensable for the design of heterojunction devices [35] [36] . Band offsets of semiconductors are important and necessary parameters in material and device design [37] . They are among the most important properties of heterostructures. Their precise knowledge is extremely important to engineer electronic [38] and optoelectronic [39] devices. More specifically, the band offsets are critical to many properties such as quantum confinement [40] , doping ability [41] , and chemical activity [42] . In the theoretical approach, the valence and conduction band offsets are formed by two terms,
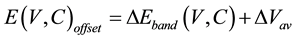 (1)
(1)
where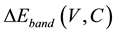 , known as the band structure contribution, is defined as the difference between the valence band maxima (VBM) and the conduction band minima (CBM) relative to the average of the electrostatic potential in each material.
, known as the band structure contribution, is defined as the difference between the valence band maxima (VBM) and the conduction band minima (CBM) relative to the average of the electrostatic potential in each material.
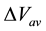 is the lineup of the average electrostatic potential across the interface [43] . Most of the heterojonction physics is determined by the band offset, which is usually described by models [44] -[46] . The model proposed by Van de Valle and Martin [47] will be used here and will be combined with ab initio calculations, which will allow us to calculate the band offset of the ZnO/Cu2O heterojunction. Previous experimental studies of this heterojonction can be found in Refs. [20] [48] , while theoretical results are reported in Ref. [22] .
is the lineup of the average electrostatic potential across the interface [43] . Most of the heterojonction physics is determined by the band offset, which is usually described by models [44] -[46] . The model proposed by Van de Valle and Martin [47] will be used here and will be combined with ab initio calculations, which will allow us to calculate the band offset of the ZnO/Cu2O heterojunction. Previous experimental studies of this heterojonction can be found in Refs. [20] [48] , while theoretical results are reported in Ref. [22] .
In this paper, we are interested first to build a supercell containing a heterojunction formed by [0001] oriented zinc oxide and cuprous oxide in the hexagonal structure (CdI2-type), and second to calculate the band alignments in ZnO/Cu2O heterojunction and compare it with any other new experimental and theoretical results. There is a need for more fundamental studies on the polar ZnO and Cu2O surfaces in order to get a better understanding of the physical properties of the heterojunction, which plays an important role in determining the properties of the interface. This theoretical calculation was performed in the framework of the DFT using pseudopotentials and a planewave basis implemented in the Abinit package.
2. Details of the Calculations
2.1. Details of the Density Functional Theory Simulations
The calculations have been performed in the framework of the Density Functional Theory [49] [50] , using pseudopotentials and a plane wave basis set as implemented in the Abinit code [51] . Abinit, which is available under a free software licence, allows one to compute a large set of useful properties of solid-state systems [52] . The valence electron wave functions have been expanded in a plane waves basis set with a kinetic energy cutoff, Ecut, of 50 Hartree. Troullier-Martins pseudopotentials [53] have been generated by mean of the Fritz-Haber-In- stitute package [54] , for the reference 3d104s2, 3d104s1 and 2s22p4 atomic configurations of zinc, copper and oxygen, respectively. Exchange-correlation energy and potential have been taken into account at the local density approximation (LDA) level by mean of the Perdew-Wang [55] parameterization of the quantum Ceperley and Alder Monte Carlo results for the homogeneous electron gas [56] . In search of a better approximation to describe the exchange-correlation density functional, we also use the Perdew-Burke-Ernzerhof (PBE) version of the generalized gradient approximation [57] . A k-point Monkhorst-Pack grid [58] has been used for the Brillouin zone sampling. For bulk calculations, a mesh of 8x8x8 was used for ZnO and Cu2O. For the ZnO/Cu2O interface and the polar surfaces ZnO (0001) and Cu2O (0001), a mesh of 8 × 8 × 2 was sufficient to reach convergence. The standard procedure for calculating interface and surface energies is the slab supercell technique, in which one needs to subtract bulk energy from total energy of slab supercell. Interface structure is modeled in a supercell geometry employing 8 layers (Figure 1). Surface structures are modeled in a supercell geometry, employing a symmetric slab consisting of 8 layers and 6 layers for ZnO and Cu2O, respectively. A vacuum region of 3c (~12Å) ensures the decoupling of repeated slabs.
2.2. Average Potential Method
The Van de Walle and Martin model [46] is the most widely used for estimating band offsets at semiconductor- semiconductor interfaces. This approach was found to be successful for a variety of materials with non polar interfaces. This model can be easily combined with DFT calculations, as the band offset can be deduced from the average self-consistent potential in the superlattice. The success of this simple model reflects the fact that the principal conclusion of the first-principle calculations is that the offsets are essentially intrinsic [59] . To visua- lize the electrostatic potential profiles extending throughout the heterostructures, V(x,y,z) is averaged on the plane perpendicular to the axis (xy-plane) using the equation,
Figure 1. Supercell model considered in the present work. ZnO crystal growth along the c-axis and Cu2O in the hexagonal structure (CdI2-type). Colorkeys, red balls-oxygen, bleue balls-copper, gray balls-zinc.
 (2)
(2)
where S represents the area of a unit cell in the xy-plane (Figure 2). The macroscopic average
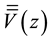 is accomplished by averaging
is accomplished by averaging
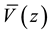 at each point over a distance corresponding to one period a,
at each point over a distance corresponding to one period a,
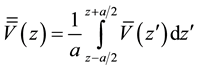 (3)
(3)
where a is the period length in the direction perpendicular to the interface. The macroscopic average potential shows a discontinuity at the interface, indicating that electrons should overcome a potential barrier to cross from ZnO section to Cu2O section. This value is given by,
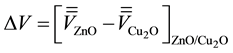 (4)
(4)
The band offset can be determined by aligning the average electrostatic potential across the interface between two segments when the average of the electrostatic potential converges to the values of their infinite materials, using the following equation,
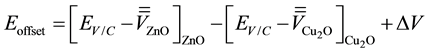 (5)
(5)
where the first and second terms represent the positions of the valence/conduction band (Ev/c) relative to those of the average electrostatic potentials for the ZnO and Cu2O, respectively. The third term indicates the difference between the two macroscopic average potential from ZnO to Cu2O (Figure 3).
2.3. Supercell of the ZnO/Cu2O Interface
The first step in the calculation of the interface properties is the construction of the supercell. The supercell has to be periodic in the three dimensions and must be large enough in order to describe both ZnO and Cu2O bulk and interface regions. In order to simulate the ZnO/Cu2O heterojunction, we have built the supercell formed by 8 layers shown in Figure 1. The structures of ZnO, Cu2O and of the ZnO/Cu2O superlattice have been fully determined. The resulting lattice parameters are reported in Table 1.
ZnO crystals generally grow along the c-axis by alternating layers of Zn2+ and O2−. This atomic arrangement along the c-axis leads to a polar crystal along the hexagonal longitudinal c-axis. This polarity imposes a growth direction for Cu2O. Several experimental and theoretical studies [22] [23] [60] [61] have demonstrated that Cu2O grows on the ZnO substrate according to the hexagonal symmetry. As under standard thermodynamic
Figure 2. Schematic diagram of the band alignment of conduction and valence band offsets in a semiconductor hetero- junction.
Figure 3. Variation of the plane and macroscopic average potential for ZnO/Cu2O in the z direction with LDA (up) and GGA-PBE(down) approximations. ∆V is the potential difference between the macroscopic average potential of ZnO and Cu2O.
Table 1. ZnO, Cu2O and ZnO/Cu2O structure parameters according to LDA and GGA-PBE approximations and to experiment.
conditions Cu2O has the cuprite structure, it is usually accepted that the growth is made in the hexagonal structure (CdI2-type) of the cubic lattice. In this study, we consider the possibility of a Cu2O growth CdI2-type, which differs from the cubic one for the stacking of the Cu and O planes. As in the CdI2-type, each O plane is between two Cu planes, this arrangement gives rise to a stoichiometric superlattice. As already noticed in the introduction, Cu2O transforms to a CdI2-type phase under pressure, as it was shown both experimentally [87] and theoretically [16] .
The atomic arrangements in the Cu2O and ZnO (0001) suggest that it is energetically favorable for Cu2O to grow on the ZnO (0001) substrate [62] . In ZnO/Cu2O heterojunction, the influences may be more obvious because of the large mismatch between cubic Cu2O (a = 4.27 Å) and wurtzite ZnO (a = 3.25 Å and c = 5.21 Å) [63] . We found a possible way of lattice matching with small lattice mismatch for Cu2O thin films deposited on ZnO substrate (Table 1). In this study, we choose the Cu2O (CdI2-type) and the ZnO (0001). In this case, the Cu2O lattice would be compressed and the Cu-O bond length is decreased which explains the choice of the high pressure phase of Cu2O.
3. Bulk Properties
Under normal conditions, ZnO in the wurtzite structure (P63mc) is the most stable polymorph. This is a hexagonal lattice belonging to the space group P63mc and is characterized by two interconnected sublattices of Zn2+ and O2− in such a way that each Zn ion is surrounded by tetrahedra of O ions, and vice-versa. This tetrahedral coordination gives rise to a polar symmetry along the hexagonal axis. This polarity is responsible for a number of ZnO properties including piezoelectricity and spontaneous polarization. It is also a key factor in crystal growth. Wurtzite structure is characterized by three parameters including the lattice constant a, the c/a ratio, and the internal parameter u [64] . Under ambient conditions, Cu2O crystallizes in a simple cubic structure, which belongs to space group Pn-3m. Under hydrostatic pressure, cuprous oxide transforms into tetragonal or hexagonal structure [23] [34] [65] . Growth constraints tend to guide Cu2O in the (111) direction. The Cu2O structure in this direction coincides well with the hexagonal structure [66] . In this work, the Cu2O structure that meets the growth of ZnO, is hexagonal type CdI2 with space group P-3m (164) [15] .
The lattice parameters and bulk modulus are determined by fitting a set of data points to the Murnaghan equation of state [46] . A fit of the resulting energy versus volume curve with the Murnaghan equation, shown in Figure 4, gives the values of B and its pressure derivative B’ = dB/dP for cuprous oxide. Our calculated lattice parameters, bulk modulus B and B’ together with other experimental values are listed in Table 1. For the cuprous oxide, LDA calculations show the well-known over-binding effect value with a lattice parameter underestimated as compared to the experimental results, and GGA-PBE calculation is overestimated. Our results are in a good agreement with the published experimental and theoretical data [23] [24] [53] [54] .
4. Surface Properties
The structural and electrical properties of nanostructures based on different semiconductors are governed by the interfaces. A microscopic understanding of physics properties (conductivity, transparency, growth processes, etc.) requires the investigation of the surface processes at an atomic level [66] . Slab model is the most popular way to model the surface. It consists of a film formed by few atomic layers parallel the crystalline plane of interest. Then, thin slabs need to repeat in one direction. To perform a supercell calculation, one defined a unit cell oriented with one axis perpendicular to the surface of interest, containing the non-equivalent atoms of a
Figure 4. Total energy vs lattice parameters for Cu2O and ZnO within LDA and GGA-PBE approximations. A Murnaghan fit on the curves (full line) has been applied to extract equilibrium lattice parameter and bulk modulus.
crystalline thin film and some vacuum layers.
In the ab initio calculations and using a supercell model containing slabs with two equivalent surfaces, the surface energy, Esurf at T = 0 K of a clean surface can then be calculated as,
 (6)
(6)
where Eslab and Ebulk are the total energy of the slab and the bulk, respectively. N is the number of atoms in the
slab, A is the surface unit area, and the factor
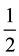 is used because the slab has two surfaces. Positions of all
is used because the slab has two surfaces. Positions of all
atoms were relaxed during calculations of Eslab. ESurf is converged with respect to the vacuum thickness, in order to rule out undesired surface interactions either through the bulk material or through the separating vacuum.
ZnO crystallizes in the wurtzite structure. When the crystal is cleaved normal to the c-axis in a manner which breaks the interatomic bonds, two different polar surfaces are formed on opposite sides of the crystal, each hav-
ing only one type of ion in its outermost plane. The theoretical study of ZnO surfaces may hold the key to un-
derstanding the experimental results. The polar (0001) and (000-1) surface of ZnO has previously been studied using many methods and under various approximations [26] . The zinc cations are in the outer atomic layer of the (0001)-Zn surface and the oxygen anions outermost on the (000-1)-O surface. These two ZnO surfaces are mod- eled using periodic supercells. 8 atomic layers were used in the calculations to represent a 2-dimensional (1 × 1) surface unit cell a = b. The lattice parameters are already calculated with LDA and GGA-PBE approximations (Table 1). A vacuum layer of 3c (~15Å) was inserted in the direction perpendicular to the surface, at such a dis- tance there was little interaction between the neighboring layers. The surface energies of the (0001)-Zn and (000-1)-O surfaces are computed with the LDA and GGA-PBE approximations (Table 2). The LDA surface
Table 2. Surface energies computed in LDA and GGA-PBE for (0001) surfaces of the ZnO and Cu2O, in J/m2.
energies calculated for the (0001)-Zn surface and (000-1)-O are 1.64 J/m2 and 1.68 J/m2, respectively. These values are underestimated when compared with experimental values (Table 2). Comparison of the results of LDA and GGA-PBE calculations of the surface energies shows that the latter method is in a good agreement with experimental values. GGA-PBE is best suited because the atomic bonding in ZnO, in the c-axis, is largely ionic which produces an asymmetry of the charge distribution.
Cu2O surface have been studied with great interest [67] [68] . Quite many ab initio studies of low-index surfaces of Cu2O were performed recently [33] [69] [70] . The polar Cu2O (111) surface could be prepared as Cu-rich or O-rich (depending on the O exposure) and was found to exhibit various reconstruction patterns on the oxidation degree and annealing history [68] . In this study, we considered the Cu2O in the structure CdI2-type. Cu2O (0001) surface consists of 2 copper layers sandwiched between one layer of oxygen. We are interested in the calculation of the surface energies of Cu2O (0001)-Cu surface and Cu2O (0001)-O surface. These surfaces are modeled using periodic supercells containing 8 atomic layers. A vacuum layer of 3c (~12Å) is sufficient to neglect interaction between the neighboring layers. The surface energies of the Cu2O (0001)-Cu surface and Cu2O (0001)-O surface are computed with the LDA and GGA-PBE approximations (Table 2). The GGA-PBE surface energies calculated for the Cu2O (0001)-Cu surface and Cu2O (0001)-O surface are 1.78 J/m2 and 1.35 J/m2, respectively. In our calculation, we observe a good agreement for the surface energies. For Cu2O, it is not simple to compare our results with available experimental and theoretical results because our choice of hexagonal structure of this oxide while the others take a cubic structure along the [111] direction.
5. Work Function
Consider nanoscale constructions, such as self assembled monolayers, where the underlying oxide workfunctions (and Fermi energy) are crucial to determine interfacial phenomena [81] . Thus, it becomes critical to have a clear understanding of the fundamental properties of the oxides starting from surface energies and workfunctions. The workfunction is the minimum energy needed to remove an electron from the bulk of a material through a surface to a point outside the material, and can be written as,

where Vvac is the potential in the vacuum region and Ef is the Fermi energy. In practice, this is the energy required at 0 K to remove an electron from the Fermi level of the oxide to the vacuum level [82] . Calculations of workfunction using DFT employ this definition and determine the Fermi energy and vacuum potential from calculations of the metals in slab supercell geometries. However, workfunctions calculated with slab approximations are known to have a dependency on the thickness of the slab, thus further analysis is required to extract bulk metal work functions from slab approximation. This dependency is well documented in some cases and is attributed to finite size effects arising from classical electrostatic interactions or from quantum size effects [83] [84] . Methodology to lessen such effects is available in the literature [85] .
We used DFT method with LDA and GGA-PBE to investigate the workfunction of ZnO and Cu2O. We investigated the workfunction values on different ZnO and Cu2O surfaces. We calculated workfunctions of the surfaces in ZnO (0001). This orientation is characterized by two polar surfaces, Zn terminated and O terminated. While Cu2O in the CdI2-type structure has two polar surfaces, Cu terminated and O terminated. The calculated workfunctions of the ZnO and Cu2O, in the different terminations, are presented in Table 2. We can draw from this table. First, workfunction values of ZnO and Cu2O surfaces vary widely from study to another, following experimental or theoretical methods adopted. Our results are in the range of previous results listed in Table 2. Second, in comparison with experiment, Table 2, we find that our calculated workfunctions in most cases are larger than the measured values. This is in agreement with the fact that the calculations are performed for single, close-packed surfaces, while the experimental values are obtained from measurements on polycrystalline samples. Third, it is not simple to compare our results for Cu2O with the literature ones because we used in this work a CdI2-type- structure while the other works used cubic Cu2O (111).
6. Results and Discussion
We will first examine the atomic structures of ZnO and Cu2O materials in the wurtzite and hexagonal CdI2-type phases, respectively. We use Murnaghan equation to obtain the (a, c) lattice constants [88] [89] . The reliability of this method is demonstrated by the excellent agreement between calculated and experimental lattice constants, as listed in Table 1. Comparing our results to the experimental values, we observe that the lattice parameter values are slightly underestimated by LDA and overestimated by GGA.
Supercell method was employed in the study of the ZnO/Cu2O heterojunction. In Figure 1 the comparison of the crystallographic structures of ZnO and Cu2O seen, respectively, along the [0001] and in the hexagonal structure (CdI2-type) is shown. In the ZnO structure, both Zn and O atoms are perfectly arranged in a hexagonal symmetry, while copper and oxygen retain the hexagonal symmetry in the Cu2O structure. The interface region was modeled using a periodically repeated slab of 8 atomic layers; this is enough to reproduce a bulk-like character at both sides of the interface. The optimized lattice properties of the ZnO/Cu2O heterojunction are tabulated in Table 1. We use the same lattice constant for both materials, while compressing the lattice parameter, aZnO, of the ZnO and dilating the lattice parameter, aCu2O, of the Cu2O. The lattice parameter of the heterojunction in the z direction is the sum of the two lattice parameters of ZnO and Cu2O.
The average potential


To calculate the conduction band alignment, we have used the experimental values of the bandgap energy because theoretical values in the LDA and GGA-PBE are under estimated and give incorrect values. In this work, we have used Eg equal to 3.37 eV and 2.1 eV for ZnO and Cu2O, respectively [18] [21] . The conduction band offset, ∆Ec, is evaluated to 0.24 eV in the LDA and −0.04 eV in the GGA-PBE. Our values are in good agreement with other values, although other work has already chosen simplified structures while we choose a more realistic one [18] . Ichimura et al. [18] have built a supercell by two oxides, ZnO and Cu2O, in the same zincblende structure. This choice is a first step to study this system with less complication in the calculation and in building the supercell, however this model is not too realistic.
We have investigated the electronic properties by calculating the density of states. The total DOS are shown in Figure 5. The difference between the DOS in the cuprous and CdI2 structures is clear, especially for the O 2s orbital. The valence band top of Cu2O is mainly contributed by Cu 3d orbital, and that of ZnO is made up of the O 2p. We show in the Figure 5 that the atomic energy level of Cu 3d is higher than that of O 2p by about 3 eV. This is considered as the principal reason why the valence band maximum of Cu2O is higher than that of ZnO in the ZnO/Cu2O system.
We have studied the surface energies and workfunction for the ZnO and Cu2O. A supercell of 8 layers of ZnO and 6 layers Cu2O is built. LDA and GGA-PBE are used. The polar (0001) surface of ZnO and Cu2O, with zinc, copper and oxygen termination, show a significant difference in surface energies and in work function. Our results of the surface energies and workfunction of the cation and anion surface of the polar ZnO are in the range of the literature values (Table 2). We show a difference between our results and other works in the case of Cu2O because our choice of the crystal structure was different. The workfunction value of the Cu2O (0001)-O is significantly large which can be explained by the instability of this surface.
7. Conclusion
We performed a first principle study of the ZnO/Cu2O interface. These investigations have been carried out us-
ing the Density Functional Theory in the LDA and GGA-PBE approximations. This work was divided into three parts. The first part was devoted to the calculation of the bulk structural properties of ZnO and Cu2O. The struc- ture, including equilibrium lattice constants, bulk modulus and pressure derivative are in good agreement with other theoretical and experimental results. In the second part, the band alignment analysis is performed using the average potential and density of states. We used the method of Van de Walle and Martin to calculate the energy offset. This approach fits well with the Density Functional Theory. We began this work by constructing a su- percell containing a junction formed by ZnO/Cu2O. We selected from this work CdI2 structure of copper oxide deposited on the zinc oxide of wurtzite structure. Our calculations of the band offset gave us a value that corre- sponded to the experimental and theoretical values already published in the literature. In the third part, we investigated the surface energies and the workfunction on different ZnO and Cu2O polar surfaces. Our results are in good agreement with experimental and theoretical values for ZnO. We found a difference between our results and other works in the case of Cu2O because our choice of the crystal structure was different. This study can
Table 3. Valence band offsets obtained by LDA and PBE approximations.
Figure 5. Density of states (DOS) of bulk ZnO and Cu2O.
help to understand the effect of the surface and interface on the growth and electron transport in the heterojunctions.
Cite this paper
MabroukZemzemi,SahbiAlaya, (2015) First Principles Study of the Structural and Electronic Properties of the ZnO/Cu2O Heterojunction. Materials Sciences and Applications,06,661-675. doi: 10.4236/msa.2015.67068
References
- 1. O’Regan, B. and Grätzel, M. (1991) A Low-Cost, High-Efficiency Solar Cell Based on Dye-Sensitized Colloidal TiO2 Films. Nature, 353,737-740.
http://dx.doi.org/10.1038/353737a0 - 2. Graetzel, M., Janssen, R.A., Mitzi, D.B. and Sargent, E.H. (2012) Materials Interface Engineering for Solution-Processed Photovoltaics. Nature, 488, 304-312.
http://dx.doi.org/10.1038/nature11476 - 3. Parida, B., Iniyan, S. and Goic, R. (2011) A Review of Solar Photovoltaic Technologies. Renewable and Sustainable Energy Reviews, 15, 1625-1636.
http://dx.doi.org/10.1016/j.rser.2010.11.032 - 4. Shevaleevskiy, O. (2008) The Future of Solar Photovoltaics, a New Challenge for Chemical Physics. Pure and Applied Chemistry, 80, 2079-2089.
http://dx.doi.org/10.1351/pac200880102079 - 5. Zunger, A., Wagner, S. and Petroff, P. (1993) New Materials and Structures for Photovoltaics. Journal of Electronic Materials, 22, 3-16.
http://dx.doi.org/10.1007/BF02665719 - 6. Surek, T. (2005) Crystal Growth and Materials Research in Photovoltaics, Progress and Challenges. Journal of Crystal Growth, 275, 292-304.
http://dx.doi.org/10.1016/j.jcrysgro.2004.10.093 - 7. Loferski, J.J. (1956) Theoretical Considerations Governing the Choice of the Optimum Semiconductor for Photovoltaic Solar Energy Conversion. Journal of Applied Physics, 27, 777-784.
http://dx.doi.org/10.1063/1.1722483 - 8. Nickel, N.H. and Terukov, E. (2005) Zinc Oxide—A Material for Micro- and Optoelectronic Applications. Springer, Berlin.
http://dx.doi.org/10.1007/1-4020-3475-X - 9. Zemzemi, M. and Alaya, S. (2014) Structural, Electronic, and Fermi Surface Evolution in Zinc Oxide under High Pressure. Journal of Optoelectronics and Advanced Materials, 16, 471-475.
- 10. Look, D.C. (2001) Recent Advances in ZnO Materials and Devices. Materials Science and Engineering: B, 80, 383-387.
http://dx.doi.org/10.1016/S0921-5107(00)00604-8 - 11. Özgür, ü., Alivov, Y.I., Liu, C., Teke, A., Reshchikov, M.A., Dogan, S., Avrutin, V., Cho, S.J. and Morkoç, H. (2005) A Comprehensive Review of ZnO Materials and Devices. Journal of Applied Physics, 98, Article ID: 041301.
http://dx.doi.org/10.1063/1.1992666 - 12. Rai, B.P. (1998) Cu2O Solar Cells: A Review. Solar Cells, 25, 265-272.
http://dx.doi.org/10.1016/0379-6787(88)90065-8 - 13. Briskman, R.N. (1992) A Study of Electrodeposited Cuprous Oxide Photovoltaic Cells. Solar Energy Materials and Solar Cells, 27, 361-368.
http://dx.doi.org/10.1016/0927-0248(92)90097-9 - 14. Herion, J., Niekisch, E.A. and Scharl, G. (1980) Investigation of Metal Oxide/Cuprous Oxide Heterojunction Solar Cells. Solar Energy Materials, 4, 101-112.
http://dx.doi.org/10.1016/0165-1633(80)90022-2 - 15. Zemzemi, M., Alaya, S. and Ben Ayadi, Z. (2014) Ab Initio Study of Heterojunction Discontinuities in the ZnO/Cu2O System. Journal of Experimental and Theoretical Physics, 118, 945-950.
http://dx.doi.org/10.1134/S1063776114050185 - 16. Minami, T., Nishi, Y., Miyata, T. and Nomoto, J. (2011) High-Efficiency Oxide Solar Cells with ZnO/Cu2O Heterojunction Fabricated on Thermally Oxidized Cu2O Sheets. Applied Physics Express, 4, Article ID: 062301.
http://dx.doi.org/10.1143/APEX.4.062301 - 17. Kramm, B., Laufer, A., Reppin, D., Kronenberger, A., Hering, P., Polity, A. and Meyer, B.K. (2012) The Band Alignment of Cu2O/ZnO and Cu2O/GaN Heterostructures. Applied Physics Letters, 100, Article ID: 094102.
http://dx.doi.org/10.1063/1.3685719 - 18. Jeong, S.S., Mittiga, A., Salza, E., Masci, A. and Passerini, S. (2008) Electrodeposited ZnO/Cu2O Heterojunction Solar Cells. Electrochimica Acta, 53, 2226-2231.
http://dx.doi.org/10.1016/j.electacta.2007.09.030 - 19. Ichimura, M. and Song, Y. (2011) Band Alignment at the Cu2O/ZnO Heterojunction. Japanese Journal of Applied Physics, 50, Article ID: 051002.
http://dx.doi.org/10.7567/JJAP.50.051002 - 20. Noda, S., Shima, H. and Akinaga, H. (2013) Cu2O/ZnO Heterojunction Solar Cells Fabricated by Magnetron-Sputter Deposition Method Films Using Sintered Ceramics Targets. Journal of Physics: Conference Series, 433, Article ID: 012027.
http://dx.doi.org/10.1088/1742-6596/433/1/012027 - 21. Akimoto, K., Ishizuka, S., Yanagita, M., Nawa, N., Paul, G.K. and Sakurai, T. (2006) Thin Film Deposition of Cu2O and Application for Solar Cells. Solar Energy, 80, 715-722.
http://dx.doi.org/10.1016/j.solener.2005.10.012 - 22. Ozawa, K., Oba, Y. and Adamoto, K. (2009) Formation and Characterization of the Cu2O Overlayer on Zn-Terminated ZnO (0001). Surface Science, 603, 2163-2170.
http://dx.doi.org/10.1016/j.susc.2009.04.027 - 23. Machon, D., Sinitsyn, V.V., Dmitriev, V.P., Bdikin, I.K., Dubrovinsky, L., Kuleshov, I.V., Ponyatovsky, G. and Weber, H.P. (2003) Structural Transitions in Cu2O at Pressures up to 11 GPa. Journal of Physics: Condensed Matter, 15, 7227-7235.
http://dx.doi.org/10.1088/0953-8984/15/43/007 - 24. Bechstedt, F. (2003) Principles of Surface Physics. Springer-Verlag, Berlin.
http://dx.doi.org/10.1007/978-3-642-55466-7 - 25. Holec, D. and Mayrhofer, P.H. (2012) Surface Energies of AlN Allotropes from First Principles. Scripta Materialia, 67, 760-762.
http://dx.doi.org/10.1016/j.scriptamat.2012.07.027 - 26. Meyer, B. and Marx, D. (2003) Density Functional Study of the Structure and Stability of ZnO Surfaces. Physical Review B, 67, Article ID: 035403.
http://dx.doi.org/10.1103/PhysRevB.67.035403 - 27. Soon, A., Sohnel, T. and Idriss, H. (2005) Plane-Wave Pseudopotential Density Functional Theory Periodic Slab Calculations of CO Adsorption on Cu2O (111) Surface. Surface Science, 579, 131-140.
http://dx.doi.org/10.1016/j.susc.2005.01.038 - 28. Duan, Y., Zhang, K.M. and Xie, X.D. (1994) Theoretical Studies of CO and NO on CuO and Cu2O (110) Surfaces. Surface Science, 321, 249-254.
http://dx.doi.org/10.1016/0039-6028(94)90183-X - 29. Bredow, T. and Pacchioni, G. (1997) Comparative Periodic and Cluster Ab Initio Study on Cu2O (111)/CO. Surface Science, 373, 21-32.
http://dx.doi.org/10.1016/S0039-6028(96)01147-8 - 30. Yang, Y., Schlepütz, C.M., Bellucci, F., Allen, M.W., Durbin, S.M. and Clarke, R. (2013) Structural Investigation of ZnO-Polar (000-1) Surfaces and Schottky Interfacs. Surface Science, 610, 22-26.
http://dx.doi.org/10.1016/j.susc.2012.12.018 - 31. Schulz, K.H. and Cox, D.F. (1991) Photoemission and Low-Energy-Electron-Diffraction Study of Clean and Oxygen-Dosed Cu2O (111) and (100) Surfaces. Physical Review B, 43, 1610-1621.
http://dx.doi.org/10.1103/PhysRevB.43.1610 - 32. Soltys, J., Piechota, J., Lopuszyński, M. and Krukowski, S. (2013) Density Functional Theory (DFT) Study of Zn, O2 and O Adsorption on Polar ZnO (0001) and ZnO (000-1) Surfaces. Journal of Crystal Growth, 374, 53-59.
http://dx.doi.org/10.1016/j.jcrysgro.2013.03.048 - 33. Islam, M.M., Diawara, B., Maurice, V. and Marcus, P. (2009) First Principles Investigation on the Stabilization Mechanisms of the Polar Copper Terminated Cu2O (1 1 1) Surface. Surface Science, 603, 2087-2095.
http://dx.doi.org/10.1016/j.susc.2009.04.005 - 34. Cortona, P. and Mebarki, M. (2011) Cu2O Behavior under Pressure, an Ab Initio Study. Journal of Physics: Condensed Matter, 23, Article ID: 045502.
http://dx.doi.org/10.1088/0953-8984/23/4/045502 - 35. Bernardini, F. and Fiorentini, V. (1998) Macroscopic Polarization and Band Offsets at Nitride Heterojunctions. Physical Review B, 57, 9427-9430.
http://dx.doi.org/10.1103/PhysRevB.57.R9427 - 36. Wei, S.-H. and Zunger, A. (1998) Calculated Natural Band Offsets of All II-VI and III-V Semiconductors, Chemical Trends and the Role of Cation d Orbitals. Applied Physics Letters, 72, 2011.
http://dx.doi.org/10.1063/1.121249 - 37. Franciosi, A. and Van de Walle, C.G. (1996) Heterojunction Band Offset Engineering. Surface Science Reports, 25, 1-140.
http://dx.doi.org/10.1016/0167-5729(95)00008-9 - 38. Wilk, G.D., Wallace, R.M. and Anthony, J.M. (2001) High-κ Gate Dielectrics, Current Status and Materials Properties Considerations. Journal of Applied Physics, 89, 5243.
http://dx.doi.org/10.1063/1.1361065 - 39. Morteani, A.C., Sreearunothai, P., Hertz, L.M., Friend, R.H. and Silva, C. (2004) Exciton Regeneration at Polymeric Semiconductor Heterojunctions. Physical Review Letters, 92, Article ID: 247402.
http://dx.doi.org/10.1103/PhysRevLett.92.247402 - 40. Li, J. and Wang, L. (2004) Deformation Potentials of CdSe Quantum Dots. Applied Physics Letters, 85, 2929.
http://dx.doi.org/10.1063/1.1800288 - 41. Zhang, S.B., Wei, S.H. and Zunger, A. (2000) Microscopic Origin of the Phenomenological Equilibrium “Doping Limit Rule” in N-Type III-V Semiconductors. Physical Review Letters, 84, 1232.
http://dx.doi.org/10.1103/PhysRevLett.84.1232 - 42. Kavan, L., Graetzel, M., Gilbert, S.E., Klemenz, C. and Scheel, H.J. (1996) Electrochemical and Photoelectrochemical Investigation of Single-Crystal Anatase. Journal of the American Chemical Society, 118, 6716-6723.
http://dx.doi.org/10.1021/ja954172l - 43. Shaltaf, R., Rignanese, G.M., Gonze, X., Giustino, F. and Pasquarello, A. (2008) Band Offsets at the Si/SiO2 Interface from Many-Body Perturbation Theory. Physical Review Letters, 100, Article ID: 186401.
http://dx.doi.org/10.1103/PhysRevLett.100.186401 - 44. Tersoff, J. (1984) Theory of Semiconductor Heterojunctions, The Role of Quantum Dipoles. Physical Review B, 30, 4874-4877.
http://dx.doi.org/10.1103/PhysRevB.30.4874 - 45. Cordona, M. and Christensen, N.E. (1987) Acoustic Deformation Potentials and Heterostructure Band Offsets in Semiconductors. Physical Review B, 35, 6182-6194.
http://dx.doi.org/10.1103/PhysRevB.35.6182 - 46. Hybertsen, M.S. (1990) Role of Interface Strain in a Lattice-Matched Heterostructure. Physical Review Letters, 64, 555-558.
http://dx.doi.org/10.1103/PhysRevLett.64.555 - 47. Van de Walle, C.G. and Martin, R.M. (1986) Theoretical Calculations of Heterojunction Discontinuities in the Si/Ge System. Physical Review B, 34, 5621-5634.
http://dx.doi.org/10.1103/PhysRevB.34.5621 - 48. Wong, L.M., Chiam, S.Y., Huang, J.Q., Wang, S.J., Pan, J.S. and Chim, W.K. (2010) Growth of Cu2O on Ga-Doped ZnO and Their Interface Energy Alignment for Thin Film Solar Cells. Journal of Applied Physics, 108, Article ID: 033702.
http://dx.doi.org/10.1063/1.3465445 - 49. Hohenberg, P. and Kohn, W. (1964) Inhomogeneous Electron Gas. Physical Review, 136, B864.
- 50. Kohn, W. and Sham, L.J. (1965) Quantum Density Oscillations in an Inhomogeneous Electron Gas. Physical Review, 140, A1133-A1138.
http://dx.doi.org/10.1103/PhysRev.140.A1133 - 51. Sharia, O., Demkov, A.A., Bersuker, G. and Lee, B.H. (2007) Theoretical Study of the Insulator/Insulator Interface, Band Alignment at the SiO2/HfO2 Junction. Physical Review B, 75, Article ID: 035306.
http://dx.doi.org/10.1103/PhysRevB.75.035306 - 52. 52Gonze, X., Beuken, J.-M., Caracas, R., Detraux, F., Fuchs, M., Rignanese, G.-M., et al. (2002) First-Principles Computation of Material Properties: The ABINIT Software Project. Computational Materials Science, 25, 478-492.
http,//www.abinit.org
http://dx.doi.org/10.1016/S0927-0256(02)00325-7 - 53. Gonze, X., Amadon, B., Anglade, P.-M., Beuken, J.-M., Bottin, F., Boulanger, P., et al. (2009) ABINIT: First-Principles Approach to Material and Nanosystem Properties. Computer Physics Communications, 180, 2582-2615.
http://dx.doi.org/10.1016/j.cpc.2009.07.007 - 54. Troullier, N. and Martins, J.L. (1991) Efficient Pseudopotentials for Plane-Wave Calculations. Physical Review B, 43, 1993-2006.
http://dx.doi.org/10.1103/PhysRevB.43.1993 - 55. Fuchs, M. and Scheffler, M. (1999) Ab Initio Pseudopotentials for Electronic Structure Calculations of Poly-Atomic Systems Using Density-Functional Theory. Computer Physics Communications, 119, 67-98.
http://dx.doi.org/10.1016/S0010-4655(98)00201-X - 56. Perdew, J.P. and Wang, Y. (1992) Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Physical Review B, 45, 13244-13249.
http://dx.doi.org/10.1103/PhysRevB.45.13244 - 57. Ceperley, D.M. and Alder, B.J. (1980) Ground State of the Electron Gas by a Stochastic Method. Physical Review Letters, 45, 566-569.
http://dx.doi.org/10.1103/PhysRevLett.45.566 - 58. Perdew, J.P., Burke, K. and Ernzerhof, M. (1996) Generalized Gradient Approximation Made Simple. Physical Review Letters, 77, 3865-3868.
http://dx.doi.org/10.1103/PhysRevLett.77.3865 - 59. Monkhorst, H.J. and Pack, J.D. (1976) Special Points for Brillouin-Zone Integrations. Physical Review B, 13, 5188-5192.
http://dx.doi.org/10.1103/PhysRevB.13.5188 - 60. Jeong, S.H. and Aydil, E.S. (2009) Heteroepitaxial Growth of Cu2O Thin Film on ZnO by Metal Organic Chemical Vapor Deposition. Journal of Crystal Growth, 311, 4188-4192.
http://dx.doi.org/10.1016/j.jcrysgro.2009.07.020 - 61. Fariza, B.M., Sasano, J., Shinagawa, T., Watase, S. and Izaki, M. (2012) Light-Assisted Electrochemical Construction of (111)Cu2O/(0001)ZnO Heterojunction. Thin Solid Films, 520, 2261-2264.
http://dx.doi.org/10.1016/j.tsf.2011.09.022 - 62. Yang, M.J., Zhu, L.P., Li, Y.G., Cao, L. and Guo, Y.M. (2013) Asymmetric Interface Band Alignments of Cu2O/ZnO and ZnO/Cu2O Heterojunctions. Journal of Alloys and Compounds, 578, 143-147.
http://dx.doi.org/10.1016/j.jallcom.2013.05.033 - 63. Akimoto, K., Ishizuka, S., Yanagita, M., Nawa, N., Paul, G.K. and Sakurai, T. (2000) Thin Film Deposition of Cu2O and Application for Solar Cells. Solar Energy, 80, 715-722.
http://dx.doi.org/10.1016/j.solener.2005.10.012 - 64. Pearson, W.B. (1958) Handbook of Lattice Spacings and Structures of Metals and Alloys. Pergamon Press, Belfast.
- 65. Zemzemi, M., ElGhoul, N., Khirouni, K. and Alaya, S. (2014) First-Principle Study of the Structural, Electronic, and Thermodynamic Properties of Cuprous Oxide under Pressure. Journal of Experimental and Theoretical Physics, 118, 235-241.
http://dx.doi.org/10.1134/S1063776114020228 - 66. Werner, A. and Hochheimer, H.D. (1982) High Pressure X-Ray Study of Cu2O and Ag2O. Physical Review B, 25, 5929-5934.
http://dx.doi.org/10.1103/PhysRevB.25.5929 - 67. Onsten, A., Mansson, M., Muro, T., Matsushita, T., Nakamura, T., Kinoshita, T., Karlsson, O.U. and Tjernberg, O. (2009) Probing the Valence Band Structure of Cu2O Using High-Energy Angle-Resolved Photoelectron Spectroscopy. Physical Review B, 76, 115-127.
http://dx.doi.org/10.1103/PhysRevB.76.115127 - 68. Cox, D. and Schulz, K.H. (1991) H2O Adsorption on Cu2O (100). Surface Science, 256, 67-76.
http://dx.doi.org/10.1016/0039-6028(91)91200-H - 69. Soon, A., Todorova, M., Delly, B. and Stampfl, C. (2006) Oxygen Adsorption and Stability of Surface Oxides on Cu (111): A First-Principles Investigation. Physical Review B, 73, Article ID: 165424.
http://dx.doi.org/10.1103/PhysRevB.73.165424 - 70. Altarawneh, M., Radney, M., Smith, P.V., Mackie, J.C., Kennedy, E.M., Dlugogorski, B.Z., Soon, A. and Stampfl, C. (2009) A First-Principles Density Functional Study of Chlorophenol Adsorption on Cu2O (110), CuO. The Journal of Chemical Physics, 130, Article ID: 184505.
http://dx.doi.org/10.1063/1.3123534 - 71. Kuo, F.L., Li, Y., Solomon, M., Du, J. and Shepherd, N.D. (2012) Workfunction Tuning of Zinc Oxide Films by Argon Sputtering and Oxygen Plasma: An Experimental and Computational Study. Journal of Physics D: Applied Physics, 45, Article ID: 065301.
http://dx.doi.org/10.1088/0022-3727/45/6/065301 - 72. Kim, T., Yoshitake, M., Yagyu, S., Nemsák, S., Nagata, T. and Chikyow, T. (2010) XPS Study on Band Alignment at Pt-O-Terminated ZnO (000-1) Interface. Surface and Interface Analysis, 42, 1528-1531.
http://dx.doi.org/10.1002/sia.3601 - 73. Jacobi, K., Zwicker, G. and Gutmann, A. (1984) Work Function, Electron Affinity and Band Bending of Zinc Oxide Surfaces. Surface Science, 141, 109-125.
http://dx.doi.org/10.1016/0039-6028(84)90199-7 - 74. Schlesinger, R., Xu, Y., Hofmann, O.T., Winkler, S., Frisch, J., Niederhausen, J., Vollmer, A., Blumstengel, S., Henneberger, F., Rinke, P., Scheffler, M. and Koch, N. (2013) Controlling the Work Function of ZnO and the Energy-Level Alignment at the Interface to Organic Semiconductors with a Molecular Electron Acceptor. Physical Review B, 87, Article ID: 155311.
http://dx.doi.org/10.1103/PhysRevB.87.155311 - 75. Marien, J. (1976) Field Emission Study of the Specificity of Zinc Oxide Polar Surfaces (0001) and (0001). Work Function and Hydrogen Adsorption. Physica Status Solidi (a), 38, 513-522.
http://dx.doi.org/10.1002/pssa.2210380211 - 76. Wander, A., Schedin, F., Steadman, P., Norris, A., McGrath, R., Turner, T.S., Thornton, G. and Harrison, N.M. (2001) Stability of Polar Oxide Surfaces. Physical Review Letters, 86, 3811-3814.
http://dx.doi.org/10.1103/PhysRevLett.86.3811 - 77. Na, S.-H. and Park, C.-H. (2010) First-Principles Study of the Surface Energy and Atom Cohesion of Wurtzite ZnO and ZnS-Implications for Nanostructure Formation. Journal of the Korean Physical Society, 56, 498-502.
http://dx.doi.org/10.3938/jkps.56.498 - 78. Soon, A., Todorova, M., Delly, B. and Stampfl, C. (2007) Thermodynamic Stability and Structure of Copper Oxide Surfaces: A First-Principles Investigation. Physical Review B, 75, Article ID: 125420.
http://dx.doi.org/10.1103/PhysRevB.75.125420 - 79. Yang, W.Y. and Rhee, S.W. (2007) Effect of Electrode Material on the Resistance Switching of Cu2O Film. Applied Physics Letters, 91, Article ID: 232907.
http://dx.doi.org/10.1063/1.2822403 - 80. Soon, A., Sohnel, T. and Idriss, H. (2005) Plane-Wave Pseudopotential Density Functional Theory Periodic Slab Calculations of CO Adsorption on Cu2O (111) Surface. Surface Science, 579, 131-140.
http://dx.doi.org/10.1016/j.susc.2005.01.038 - 81. Heimel, G., Romaner, L., Bredas, J.L. and Zojer, E. (2006) Interface Energetics and Level Alignment at Covalent Metal-Molecule Junctions: Π-Conjugated Thiols on Gold. Physical Review Letters, 96, Article ID: 196806.
http://dx.doi.org/10.1103/PhysRevLett.96.196806 - 82. Lang, N.D. and Kohn, W. (1971) Theory of Metal Surfaces: Work Function. Physical Review B, 3, 1215-1223.
http://dx.doi.org/10.1103/PhysRevB.3.1215 - 83. Feibelman, P.J. and Hamann, D.R. (1984) Quantum-Size Effects in Work Functions of Free-Standing and Adsorbed Thin Metal Films. Physical Review B, 29, 6463-6467.
http://dx.doi.org/10.1103/PhysRevB.29.6463 - 84. Ciraci, S. and Batra, I.P. (1986) Theory of the Quantum Size Effect in Simple Metals. Physical Review B, 33, 4294-4297.
http://dx.doi.org/10.1103/PhysRevB.33.4294 - 85. Fall, C., Binggeli, N. and Baldereschi, A. (1999) Deriving Accurate Work Functions from Thin-Slab Calculations. Journal of Physics: Condensed Matter, 11, 2689-2696.
http://dx.doi.org/10.1088/0953-8984/11/13/006 - 86. Desgreniers, S. (1998) High-Density Phases of ZnO: Structural and Compressive Parameters. Physical Review B, 58, 14102-14105.
http://dx.doi.org/10.1103/PhysRevB.58.14102 - 87. Zhang, D.K., Liu, Y.C., Liu, Y.L. and Yang, H. (2004) The Electrical Properties and the Interfaces of Cu2O/ZnO/ITO p-i-n Heterojunction. Physica B, 351, 178-183.
http://dx.doi.org/10.1016/j.physb.2004.06.003 - 88. Murnaghan, F. (1944) The Compressibility of Media under Extreme Pressures. Proceedings of the National Academy of Sciences of the United States of America, 30, 244-247.
http://dx.doi.org/10.1073/pnas.30.9.244 - 89. Hebbache, M. and Zemzemi, M. (2004) Ab Initio Study of High-Pressure Behavior of a Low Compressibility Metal and a Hard Material, Osmium and Diamond. Physical Review B, 70, Article ID: 224107.
http://dx.doi.org/10.1103/PhysRevB.70.224107 - 90. Lee, H. and Martin, R.M. (1997) Applications of the Generalized-Gradient Approximation to Atoms, Clusters, and Solids. Physical Review B, 56, 7197-7205.
http://dx.doi.org/10.1103/PhysRevB.56.7197 - 91. Gillen, R. and Robertson, J. (2013) Accurate Screened Exchange Band Structures for the Transition Metal Monoxides MnO, FeO, CoO and NiO. Journal of Physics: Condensed Matter, 25, Article ID: 165502.
http://dx.doi.org/10.1088/0953-8984/25/16/165502 - 92. Kümmel, S. and Kronik, L. (2008) Orbital-Dependent Density Functionals: Theory and Applications. Reviews of Modern Physics, 80, 3-60.
http://dx.doi.org/10.1103/RevModPhys.80.3







