ABSTRACT

Based on the special theory of relativity in space-like continuum, the present author points that if there exist tachyons in nature, they should be neutral point-like particles with lepton appearance, which are very much like our early understanding about neutrinos before. The author also points that an alternative explanation for neutrino oscillations may be the conversion between mass-less neutrinos with different flavors expressed in different “lowest limited momentum” during their flight journey, which originates from that the argument in the squared sine function of the probability of neutrino oscillation may be less than zero, which is mathematical foresight and may not be ignored.

Keywords:

Neutrino Oscillations, Space-Like Continuum, Tachyon, Lorentz Invariance, Energy-Momentum Relation, Lowest Limited Momentum, Time-Like Representation, Face-Changing Effect

1. Introduction

The knowledge of truth is not accomplished once, nor can it be accomplished in a short time. Often correct scientific knowledge can be arrived at only after many repetitions of the process leading from theoretical thinking to experimental verification and application and then back to theoretical thinking, that is, leading from practice to knowledge and then back to practice. Therefore, tell the truth, the complete system of the special theory of relativity (SR) has not been completed, although the foundation of SR has been laid for over 100 years. In fact, many of our explorations in physics today have gone astray because we have not fully, comprehensively and accurately grasped the theoretical foundations created by our predecessors, and developed and completed the system of SR that they proposed but failed to perfect. An important instance is neutrino riddles, even the neutrino research has won the Nobel Prize in physics three times, but neutrino oscillation seems to be still in very contradiction with the Standard Model of particle physics (SM). In September 2011 and in November 2011, the OPERA collaboration professed that their experiments and subsequent repeated experiments show velocities of 17 GeV and 28 GeV neutrinos exceeding the speed of light. Shortly afterwards, a dramatic denial of the results occurred: in February 2012, reports came out that OPERA’s results may have been caused by a loose fiber optic cable attached to one of the atomic clocks which measured the departure and arrival times of the neutrinos. In June 2012, CERN announced that new measurements conducted by all four Gran Sasso experiments (OPERA, ICARUS, Borexino and LVD) found agreement between the speed of light and the speed of neutrinos, finally refuting the initial OPERA claim [1] . However, whether they measured the speed of neutrinos at the speed of light or exceeding the speed of light were not crucial to solving the very contradiction between SM and the neutrino oscillations.

We should remember that at the Congress of Scientists, Cologne, 21 Sept. 1908, Minkowski delivered his famous lecture “Space and Time” [2] . In this lecture, Minkowski not only gave an extraordinarily elegant form to Einstein’s SR [3] , but has also expanded Einstein’s time-like SR ( $\text{d}{s}^2>0$ ―bradyons) to space-like ( $\text{d}{s}^2<0$ ―tachyons) and light-like ( $\text{d}{s}^2=0$ ―luxons) space-time continuum, where

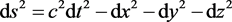, (1)

is square of the space-time distance ds between two infinitesimally near space-time points. Of course, Einstein laid the foundation of SR and established the well-known parts of SR in the present physics textbooks from 1905 until today just for bradyons with rest-mass only, those physics contained in space-like and light-like regions are not fully revealed. Actually, under the same theoretical framework, we do not possess any reliable physical reasons to deny the reality of space-like and light-like physics where the key to solving the very contradiction between SM and the neutrino oscillations might be lie in.

In Section 2, based solely the Lorentz invariance of Minkowski’s space-like, metric, except spin, the fundamental physical properties of tachyon are given. In Section 3, the relativistic energy-momentum relation for a free tachyon is derived. In Section 4, some important physical relations for tachyon are given. In Section 5, the author expounds and proves the fact of neutrino oscillations is not sure that the neutrino must have a nonzero rest mass, neutrino oscillation ${\nu }_{\mathcal{l}}\to {\nu }_{{\mathcal{l}}^{\prime }}$ may be the conversion between mass-less neutrinos with different flavors expressed in different space-like physical quantities “lowest limited momentum $p_{0{\mathcal{l}}^{\prime }}$ in their flight. In Section 6, in order to confirm whether neutrinos being tachyons or not, the present author makes some suggestions.

2. The Fundamental Physical Appearance of Tachyon

Since early 1960s in last century, some pioneers studied the physics of tachyons [4] [5] [6] and the shape of tachyons [7] , but it was a pity that they treated tachyons and their motion by means of those concepts in the time-like region. Consequently, it is difficult to understand their thesis not only those normal physical quantities with imaginary values, but also those physical properties of contradictions. In reality, it is very surprise to us, as long as to adhere the Lorentz invariance of Minkowski’s space-like metric ( $\text{d}{s}^2<0$ ), it is obtained naturally that if there exist tachyons in nature, these tachyons must move with superluminal speed in any frames of reference. That is to say, it is impossible that there exists a relative static coordinate system within tachyons. As a result, tachyons would be particles without structure, namely, they would be particles without size, volume, rest mass, electric charge and magnetic moment. Therefore, if there exist tachyons in nature, they should be neutral point-like particles with lepton appearance, which are very much like our early understanding about neutrinos before. As for the half-integer spin of neutrino, it has been determined by the conservation equation of the total angular momentum in certain types of radioactive decay in some nuclear reactions. Whether a tachyon has spin or not? It needs to be determined experimentally, and can not be obtained from Lorentz invariance of Minkowski’s space-like metric.

3. The Relativistic Energy-Momentum Relation for a Free Tachyon

Fortunately, there is no need to know more complete space-like physics, it is enough to discuss the issue in this paper only to take into account the relativistic energy momentum relationship of free tachyons.

For two frames of reference $\Sigma$ and ${\Sigma }^{\prime }$ , the metric tensor is

$g_{\mu \nu }=g^{\mu \nu }=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& -1& 0& 0\\ 0& 0& -1& 0\\ 0& 0& 0& -1\end{array}\right)$ .

Contravariant coordinate is:

$x^{\mu }\equiv \left(x^0,x^1,x^2,x^3\right)\equiv \left(x^0,x\right)$ .

Covariant coordinate is:

$x_{\mu }\equiv \left(x_0,x_1,x_2,x_3\right)\equiv \left(x_0,-x\right)=g_{\mu \nu }{x}^{\nu }$ .

For any four-vector $A_{\mu }$ ,to denote the scalar (or inner) product $A^2$ by

$A^2=A_{\mu }{A}^{\mu }=A_0^2-A^2$ .

Because of this, for a momentum four-vector

$p^{\mu }=\left(E/c,p_x,p_y,p_z\right)\equiv \left(p^0,p\right)$ ,

the inner product 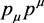is

$p^2=p_{\mu }{p}^{\mu }=E^2/c^2-{\left|p\right|}^2\{\begin{array}{l}>0,~\text{time-like}\\ =0,~\text{light-like}\\ <0,~\text{space-like}\end{array}$

In time-like region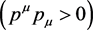, the particle being at rest, i.e.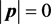, is allowed, there may exist a relative rest reference frame where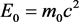, m₀ being the rest-mass. In light-like region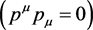, as is known to all, a photon is with zero rest-mass. For the space-like region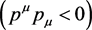, obviously, only the energy of a tachyon 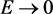is allowed. As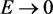, by means of p₀ indicating the “lowest limited momentum” of a tachyon [8] , the relativistic energy-momentum relationships for a free bradyon, a photon and a free tachyon are as follows

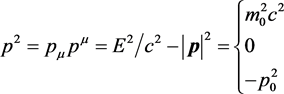(2)

4. Some Important Physical Relations for Tachyon

1) The time-like representation of lowest limited momentum p₀

In space-like region there is no physical quantity “rest-mass” m₀, but there is physical quantity “lowest limited momentum” p₀, in time-like region there is no physical quantity “lowest limited momentum” p₀, but there is physical quantity “rest-mass” m₀. According to Equation (2), one may see, if there is a need to express “lowest limited momentum “p₀ in time-like physical quantity, it must be written as an abnormal representation, that is 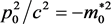or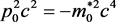. We may call the abnormal physical quantity 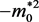(or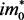) is the time-like representation of the space-like physical quantity p₀.

Actually, in the 70 s - 80 s last century, the “imaginary rest-mass” arose in theoretical studies [4] [5] [6] , and the problem of measuring directly the neutrino rest mass by investigating the end-point region of the β-spectrum of tritium also became a hot topic in the 80 s last century. The square of the neutrino mass has been measured to be negative in many experiments. For instance, in [9] the published result was

,

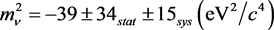and the world average given by the Particle Data Group in 1994 was

.

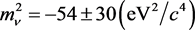In [10] the measured result by A.I. Belesev et al. was

.

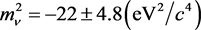In 1999, Ch. Weinheimer et al. claimed that their high precision measurement led to [11] :

.

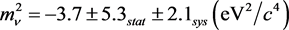In [12] V. Lobashev et al. considered that due to the presence of anomaly structure in the vicinity of the end-point energy of tritium β spectrum, except 1996, their data were

,

,

.

The combined value in quadrature was

.

In [13] , by analyzing a surface muon beam in a magnetic spectrometer equipped with a silicon microstrip detector obtained a negative squared muonneutrino mass value was

.

Now we know that makes sense, is just the time-like representation of a real space-like physical quantity. But at that time experimenters didn’t know the exact physical significance of (as), they all thought that their experiments suffered from a strange shift of the original correct data into an unphysical region.

2) Energy-velocity relationship

Note, In SR, there is no physical quantity “mass” appearing in the expression of, so that or, or are the universal physical expressions in both time-like and space-like regions, where and are the velocities of a tachyon and a bradyon respectively. From Equation (2), it follows that

. (3)

Obviously, the speed of a tachyon is a monotonic decreasing function of increasing energy E, which is very different feature from the character of the energy-velocity relationship of a bradyon

, (4)

where the speed of a bradyon is a monotonic increasing function of increasing energy E.

Aside from the history of neutrino velocity measurements since the early1980s, it is enough to use the experimental data in [14] and in its citated literature to test the correctness of Equation (3) and Equation (4). In [14] the measurement set an upper bound on the mass of the muon neutrino of 50 MeV at 99% confidence and the measurement was repeated in 2007 using the MINOS detectors, which alleged that for neutrinos of 3 GeV, the speed to be, at the 99% confidence level, in the range between, that is, between 0.999976 c and 1.000126 c. According to Equation (3), , Equation (4) gives . Although the difference is not great, but the experimental data is biased towards Equation (3). P. Adamson et al. noted in [14] that at neutrino energies of a few GeV, some theories allow, which corroborated above argument “the speed of tachyon is a monotonic decreasing function of increasing energy”.

3) Momentum-velocity relationships

According to Equation (2) it is very easy to obtain the momentum-velocity relationships for a tachyon and a bradyon respectively:

,

and

.

The speed of a tachyon is a monotonic decreasing function of increasing momentum, the speed of a bradyon is a monotonic increasing function of increasing momentum and for the same energy E, the greater the “lowest limited momentum “p₀, the greater the speed.

5. An Alternative Explanation for Neutrino Oscillations

With the preparation of those knowledge mentioned in Sec.1-Sec.3, one may solve following questions: if neutrinos are tachyons without rest mass, how to explain the neutrino oscillations from one flavor to another? what physical parameters would be used to characterize the amount of mixing between neutrinos with different flavor in flight at a given time?

It is common knowledge that a practical method for investigating neutrino oscillations was first suggested by Bruno Pontecorvo in the 1950s using an analogy with kaon oscillations. In the later days he developed the modern mathematical formulation of neutrino vacuum oscillations. Follow Pontecorvo B et al. [15] [16] , for only two kinds of significant neutrino participates, using SI units, one would be accustomed to use following function

(5)

to describe the probability of the neutrino oscillation for extremely relativistic neutrinos, where are the flavor of neutrinos (neutrinos and their anti-neutrinos), being the oscillation length, where is unit-less.

Historical experience is worth attention, although above probability formula originated from one speculation about neutrino with nonzero mass, but Equation (5) contains more physical information. It was often the case in physics. This is just the charm of mathematics. For example, in 1928, negative energy values led to Dirac’s theory of positron which was discovered by Anderson in1932.

Let us back to the point, there is no positive support for that we can certainly conclude in the argument of the squared sine function must be greater than zero. It is obvious that, if

,

then

.

Now, using SI units, , the probability of the neutrino oscillation for extremely relativistic neutrinos may be described by means of following function

(6)

where are the flavor of neutrinos (neutrinos and their antineutrinos), being the oscillation length.

Therefore from Equation (6) one may see: the fact of neutrino oscillations is not sure that the neutrino must have a nonzero rest mass, neutrino oscillation may be the conversion between mass-less neutrinos with different flavors expressed in different (neutrinos and their anti-neutrinos) during their flight journey. All of above arguments are derived from SR of space-like continuum, of course, with Lorentz symmetry.

6. Suggestion

Based on the arguments mentioned above, one would know that: all of the results of previous studies about neutrinos and neutrino oscillation do not have to change, including a two-component Weyl equation for describing neutrinos and related to the maximum parity violation discovered in 1956 by Lee and Yang. [17] [18] , so that people don’t have to worry about its truth.

There was an old saying in China: the main road is simple. In short, as long as the neutrinos were tachyons without rest-mass, which would be produced in weak interactions as chirality eigenstates and their chirality being a constant of motion. Of course, the experimental fact of neutrino oscillations would be compatible with the SM, or in other words, all the contradictions between the neutrino oscillation and the SM would be dispelled, the riddles of neutrinos would be gone with the wind. Therefore, it must be recognized that to confirm the neutrinos being tachyons is the key to make a thorough study of neutrinos and SM. How to do this very difficult job? The present author makes some suggestions as follows:

1) Actually, in the environment using time-like physical quantities, the negative squared mass values were just the evidence of the presence of tachyons. Now we don’t have to think of “the negative squared mass” as a nonphysical things, and there is no need to waste effort in eliminating “the negative squared mass” in their detection. In order to make sure this point further, we should repeat those experiments in [8] - [13] , that is to do high precision measurement of the tritium β decay spectrum near its end-point to determine the negative squared mass or to do similar jobs in [14] to determined the momentum of muons from the decay at rest by analyzing the surface muon beam, or to design other more effective measurements.

2) Repeating the classical “distance of flight/time of flight” measurement experiments is still an important test, but should note “the higher the energy, the lower the speed”, whenever possible, neutrino beams whose energy is slightly above the detector threshold should be used.

3) There are other important means of verification, such as to design more exquisite experiments to examine Equation (3)―whether the speed of neutrino being a monotonic decreasing with increasing energy or an opposite trend and to survey Equation (2)―whether or deviates from the predicted direction.

4) There is also a plausible suggestion for determine the inherent quality of neutrinos. According to SR, there may be a “face-changing effect” in nature. Hence, the author suggests that the reactor neutrino experimental groups such as Double Chooz, Daya Bay, KAM LAND, Braidwood, Diable Canyon, Krasnoyarsk, RENO and other reactor neutrino experimental groups all over the world, in addition to the current reactor experimental research to the disappearance mode of, to add a measurement study of, to seek if a few neutrinos in excess of the background might be detected. “Yes” result would reveal the neutrinos being tachyons, “no” is not. Although it is a small probability event, but there is a hope, only need time and patience. The authors will elaborate on the concept of this method in more detail elsewhere.

Acknowledgements

This work was supported by the National Science Foundation of China Grant No. U1532260. The author is very grateful to Dr. Chunlei Wang for his donation of historical literature for this study and help to deal with many chores.

Cite this paper

Ai, X.B. (2018) Look at Neutrino Oscillations in Space-Like Continuum. Journal of Modern Physics, 9, 1432-1440. https://doi.org/10.4236/jmp.2018.97087

References