ABSTRACT

A novel biophysical principle: the GM-model was revealed, describing an algorithm for coherent and non-coherent electromagnetic (EM) frequencies that either sustain or deteriorate life conditions. The particular frequency bands could be mathematically positioned on a Pythagorean scale, based on information distribution according to ratios of 2:3 in 1:2. The particular scale exhibits a core pattern of twelve eigenfrequency functions with adjacent self-similar patterns, according to octave hierarchy. In view of the current interest in coherency and entanglement in quantum biology, in the present paper, we report on a meta-analysis of 60 papers in physics that deal with the influence of electromagnetic frequencies on the promotion of entangled states in, so called, EPR experiments. Einstein, Podolsky and Rosen originated the EPR-correlation thought experiment for quantum-entangled particles, in which particles are supposed to react as one body. The meta-analyses of the EPR-experiments learned that entanglement, achieved in the experiments is real, and applied frequencies are located at discrete coherent configurations. Strikingly, all analysed EPR-data of the independent studies fit precisely in the derived scale of coherent frequency data and turned out to be virtually congruent with the above mentioned semi-harmonic EM-scale for living organisms. This implies that the same discrete coherent frequency pattern of EM quantum waves that determine local and non-local states is also applicable to biological order and that quantum entanglement is a prerequisite for life. The study may indicate that the implicate order of pilot-wave steering system, earlier postulated by David Bohm is composed of discrete entangled EM wave modalities, related to a pervading zero-point energy information field.

Keywords:

Life Algorithm, Coherent Wave Pattern, Number-Scales, Harmonics, Solitons, Quantum Mechanics, Einstein-Podolsky-Rosen, Bohm, Schrödinger, Fröhlich, Pythagoras

1. Introduction

Coherent and non-coherent scales of EM frequencies were earlier revealed by us in biological systems (see Figure 1). Living organisms are influenced by patterns of electromagnetic wave fields that promote biological order [1] [2] [3] and Appendices 3, 4, 5, 6. These frequency data were shown to comply with a semi-harmonic algorithm and separation of the apparent frequency bands in the meta-analysis was found to be statistically significant. It was assumed that the particular EM frequencies, either separate or in various combinations, induce a set of collective Fröhlich condensate states that are essential for life.

2. The Quantum-Biological Basis for Coherent and Non-Coherent EM Frequencies Scaling

It is known that living organisms are able to generate and receive electromagnetic pulses that are transferred and processed at a non-thermal level [1] [2] . Electrical interaction within and between cells is well established and the most probable candidate for a form of cellular interaction is the electromagnetic field [3] . Electrons, photons, solitons represent electromagnetically oscillations that travel along proteins, microtubules and DNA [3] [4] [5] [6] . Endogenous electromagnetic fields are induced locally in cells and in this manner interfere with local resonant oscillations by excitation of neighbouring molecules and macromolecules. Bio-solitons are conceived as self-reinforcing solitary waves, that are constituting local fields, being involved in intracellular geometric ordering and patterning, as well as in intra- and intercellular signalling.

Cellular functions are sensible to low-level sinusoidal-modulated signals of different frequencies and pulse modulations. In many biological studies, windowing, both with regard to frequency and amplitude domains, has been found and non-coherent modulations of signals have also an influence on biological properties [7] . Quantum behaviour and coherence has been found for micro- and macro-processes such as photosynthesis, magneto-reception in birds, the human sense of smell as well as photon effects in vision, all showing a non-trivial role for quantum mechanisms throughout biology [8] [9] [10] . Rieper et al. modelled the electron clouds of nucleic acids in DNA as a chain of coupled quantum harmonic oscillators with dipole-dipole interaction between nearest neighbours resulting in a van der Waals type bonding [11] . Importantly, according

to Tamulis et al. quantum entanglement might be crucial in the first stages of origins of life and evolution of the biospheres because simultaneously excitation of two prebiotic kernels in the system by appearance of two additional quantum entangled excited states, will lead to faster growth and self-replication of minimal living cells [12] . Self-assembling of photoactive prebiotic systems with observed quantum entanglement phenomena have been modelled [13] [14] [15] .

In relation to this, there is biological evidence for the studies of Fröhlich in 1968, showing that living cells employ coherent waves, called solitons for constructive interference with electromagnetic fields [4] [5] . Fröhlich inferred that biological orderings principles employ boson-like quasi-particles in biological processes, similar to condensed inorganic matter. Bose-Einstein condensation, in this manner, may serve as a method for energy storage as well as for channelling energy to specific bioprocesses such as cell division and macromolecule synthesis. A previous meta-analysis of more than 500 biomedical publications showed that the particular EM frequency data revealed typical coherent life-sustaining and non-coherent life-decaying electromagnetic frequency effects. The theoretical background of the found regularities of patterns is that nature evidently organizes its components at a highly coherent semi-harmonic like way combined with energy minimization [1] [3] . But also non-coherent patterns were revealed, that show life-decaying electromagnetic frequency effects. The underlying coherent mechanism is considered to be instrumental in the unification of first, second, and third harmonics, within a broad range of frequencies from sub Hertz till PHz for living cells.

A mathematical basis for a spectrum of discrete coherent electromagnetic (EM) frequencies was recently derived based upon research carried out for solitons [3] . Solitons are self-reinforcing solitary waves that interact with complex biological phenomena such as cellular self-organization. The soliton model is able to describe a spectrum of electromagnetism modalities that can be applied to understand the physical principles of biological effects in living cells, as caused by endogenous and exogenous electromagnetic fields and is compatible with quantum coherence [1] . It has been found that that the first, second, and third harmonics of waves can be united within a broad range of frequencies from sub Hertz till about 10²⁵ Hz by dividing 2:3 ratios and approximations thereof over 1:2 ratios [3] . The spectrum of these ratios is based upon an adapted Pythagorean calculation and at this manner scales can be derived showing coherent patterns of numbers that contain a core of twelve functions that can be expressed as: 2⁰3⁰2^m, 2⁸3⁻⁵2^m, 2⁻³3²2^m, 2⁵3⁻³2^m, 2⁻⁶3⁴2^m, 2²3⁻¹2^m, 2^0.52^m, 2⁻¹3¹2^m, 2⁷3⁻⁴2^m, 2⁻⁴3³2^m, 2⁴3⁻²2^m, 2⁻⁷3⁵2^m, in which m are integers [3] . The scale has been translated to Hz-frequencies for a broad range of adjacent frequency spectra for integer values of m, of which m are integers, and range from the lowest till the highest possible frequency present in nature (see Table 1).

As mentioned above, in addition, a non-coherent-scale could be calculated based upon the finding that non-coherent parameters are located logarithmically just in between the coherent parameters of the 12-number scales. The derived arithmetical scales exhibit sequences of unique products of integer powers of 2, 3 and a factor √2 and contains about 1500 different determinate frequency data for ordered data and more than 1500 different numbers for disordered data in a fractal setting. A correlation between the proposed coherent scale and the “hidden variables” as described in the theory of David Bohm may be at stake (see Section 6).

3. A Meta-Analyses of Literature on Electromagnetics and Quantum Entanglement

Three considerations were the starting point for the search to coherent frequencies of waves for condensed matter and living organisms: 1) a deterministic quantum wave model and the idea of Einstein that quantum randomness is not the determinant of the fabric of reality, 2) the conclusion of Schrödinger that living cells require external quantum information for their development and ecological survival, 3) the proposal of Fröhlich that living cells make use of constructive interference through so called acoustic solitons, that can be described by Bose-Einstein-statistics.

Many measurement data are now available to consider a universal wave function that is deterministic, and non-local. It is proposed to use the de Brog-lie–Bohm theory that is an interpretation of non-relativistic quantum theory that postulates an actual configuration. The actual configuration is bound to geometries, and more precise probably to nested toroidal geometries. Knowledge about frequencies of living cells and condensed matter learns that eigenfrequencies play a role, even when unobserved, and that toroidal geometry might be considered [1] [2] [3] . Making use of about 500 different scientific electromagnetic frequency data of condensed matter and living cells, published during 50 years, we establish that a deterministic quantum and deterministic electromagnetic wave system exists. In the following a number of important discoveries are treated.

3.1. De Broglie

In 1924, Louis de Broglie argued that if photons, with their wavelike properties, could be described as particles, then electrons as particles should show wave like properties with a wavelength λ, inversely proportional to their momentum (p = m_ev): λ = h/p (massive particle m_e, velocity v, momentum p, Planck constant h). This relationship is now known to hold for all types of matter: all matter exhibits properties of both particles and waves. In his theory, particle motions are determined by a wave function, that de Broglie called a “pilot wave’’. For a many-body system, the pilot wave propagates in a multidimensional “configuration space”, which is constructed from the co-ordinates of all the particles involved.

Experiments confirmed de Broglie’s assumption and led Erwin Schrödinger to derive a “wave equation” to describe the motion of de Broglie’s waves. When Schrödinger proposed the wave nature of electrons and other matter particles, he may very well have had musical harmonics in mind [16] . De Broglie showed how the different energy levels of Niels Bohr’s atomic model emerged naturally by describing electrons as standing waves of various frequencies. Schrödinger developed de Broglie’s idea further with the famous wave equation, yielding three-dimensional pulsations known as spherical harmonics. According to the physicist Max Born, it is not the electrons themselves that display wave patterns, as de Broglie and Schrödinger believed, but rather the related probability distributions that indicate their likeliest positions. Although neither Schrödinger nor Einstein were comfortable with Born’s statistical interpretation, it has persisted as the standard view [16] [17] [18] .

3.2. Einstein-Podolsky-Rosen argument

Einstein, Podolsky and Rosen, in 1935, originated the so-called Einstein-Podolsky-Rosen (EPR) correlation for quantum-entangled particles [19] . Two particles are entangled if the quantum states of the particles are coupled. In such a case, quantum entangled particles seem to react as a single body; there seems to be no separation in space and time. In order for this to occur, it requires that the communication between the two particles is instantaneous. In the Einstein-Podolsky-Roosen thought experiment, Einstein attempted to show the incompleteness of QM and tried to disprove the proposal of non-locality of quantum entangled particles, and stated that quantum science apparently must be incomplete. Therefore he came up with an alternative of “local hidden variables”. He stated that indeterminacy makes quantum theory a discontinuous and a rather statistical theory. Yet, he wanted physics to be a continuous field theory, in which all physical variables are completely and possibly locally determined by a four-dimensional field of space-time in his theory of relativity [20] . The EPR-paradox continues to fascinate also those scientists that believe that quantum indeterminacy does exist. Most published investigations related to EPR have centered the past 50 years around the testing of Bell’s theorem [21] , and used more stringent tests dealing with different sets of measurements. The experimental tests of Bell’s inequalities have now evolved closer to the ideal EPR scheme, and experimental realizations provided a way to demonstrate a type of entanglement inextricably connected with quantum non-locality [22] .

3.3. David Bohm’s Interpretation of Quantum Mechanics

The Bohmian interpretation of quantum mechanics was introduced in 1952, and later called the ontological interpretation, generally seen as an alternative to the standard Copenhagen interpretation. Bohm proposed an interpretation of the quantum mechanics that is nonlocal, causal, and does not treat systems and measuring apparatus differently [23] [24] [25] . Although rejected by many, since the 1990s the interest in Bohmian mechanics has been remarkably increased, and is more considered as a computational and interpretive working tool according to Sanz [26] .

Bohm’s interpretation of quantum physics grew out of into a major search into model based on the assumption of hidden variables. The concept is based on the principle that the state of the particles is affected by a field, which guides the motion of the particles. De Broglie called this the pilot wave, while the quantum potential is derived from the ψ-field. Mathematically, the field corresponds to the wave-function of quantum mechanics, and therefore evolves according to the Schrödinger equation in which the positions of the particles do not affect the wave function [26] . The latter aspect was reconsidered in the later work of Holland, 1996 and Valentini, 2012 [27] [28] . The de Broglie-Bohm theory, in fact is an interpretation of non-relativistic quantum theory that postulates an actual configuration, that exists even when unobserved. The quantum potential approach [11] provides a more complete exposition of the idea presented by Louis de Broglie, who postulated in 1926 that the wave function represents a pilot wave which guides a quantum particle.

All physical observables in this model are represented by linear operators operating on the state vectors in the Hilbert space, the eigenvalues of such operators are real numbers and any measurement of an observable results in getting one of its eigenvalues [29] . The actual positions of the particles evolve according to the “guiding equation”, which expresses the configuration of a system of particles evolving via a deterministic motion, as choreographed by the wave function include the velocities. The trajectories of the particles are quite different from those of classical particles, because they are guided by the wave function and the evolution of the position x and momentum k_x of a single photon has a mathematical correspondence with the quantum theory of a non-relativistic particle of mass $m=\hslash \omega /c2$ and momentum $p=\hslash k_x$ [15] [16] .

The effect of the Quantum Potential on the electron depends on its form and Bohm redefined the term in-formation. The term quantum potential, indeed, is an informational effect shared by the surroundings particles/waves and depends on its form/shape and is derived from the ψ-field [23] [25] . So Bohm’s quantum field theory model postulates determinate values of the electromagnetic field operators, in line with Bell [30] who, in his quantum field theory model, postulated determinate values of the fermion number operators.

In the Copenhagen interpretation, that is, the most widely used interpretation of quantum mechanics, the Born rule: $\rho \left(X,t\right)={\left|\Psi \left(X,t\right)\right|}^2$ defines that ρ, the probability density function of a particle equals the absolute square of the wave function Ψ and this interpretation constitutes one of the fundamental axioms of the current quantum theory. This is not the case for the De Broglie-Bohm theory, where the Born rule is not a basic law. Rather, in this theory the link between the probability density and the wave function has the status of a hypothesis, called a quantum equilibrium, which is additional to the basic principles governing the wave function, being the dynamics of the quantum particles and the Schrödinger equation, see equations 1 and [27] .

(1)

When a quantum equilibrium exists also a quantum non-equilibrium should be considered. The existence of both quantum equilibrium and non-equilibrium states has not yet been verified experimentally; also quantum non-equilibrium is so far a theoretical construct. The relevance of quantum non-equilibrium states to physics lies in the fact that this can lead to quite different predictions for results of experiments, depending on whether the De Broglie-Bohm theory or the Copenhagen interpretation is assumed to describe reality [31] . The causal interpretation of quantum mechanics was extended later on by Bohm, Vigier, Hiley, Valentini [28] and others to include stochastic properties.

As mentioned above, it is not yet known what is the nature of the Quantum Equilibrium is and how such an equilibrium is reached [32] . The quantum equilibrium and the pilot-wave structure may reflect a non-local hidden variable in a causal interpretation of quantum mechanics. Elementary Cycles Theory (ECT) of Dolce postulates that every elementary “particle” of nature is characterized by persistent intrinsic space-time periodicity [33] . In ECT the Planck energy spectrum is interpreted as an harmonic spectrum of a massless periodic phenomenon of fundamental time periodicity T (quantized energy: $E_n=n\hslash \omega =n\hslash /T$ , discretized angular frequencies: nω, and time periodicity T = h/E) [33] . According to ‘t Hooft, it is assumed that a theory describing our world starts with postulating the existence of sub-systems that in a first approximation evolve independently, and then are assumed to interact. It is suspected that our world can be understood by starting from a pre-quantized classical, or “ontological” system. If time would be assumed to be discrete, the Hamiltonian eigenvalues would turn out to be periodic [34] [35] . Both theories favor a quasi-classical and quantum ontological interpretation of quantum physics, as in a primary form earlier suggested by David Bohm and may open the way to reconcile quantum mechanics and relativity theories.

3.4. Bell’s Theorem

John Bell in theory proved that the supposed non-local effect of quantum-entangled particles was probably real, and this became known as Bell’s theorem or inequality. He resolved the paradox by pointing to a failure of local realism itself and proved the impossibility of completing quantum mechanics with local hidden variable theories [8] . Bell’s theorem ruled out local hidden variables as a viable explanation of quantum mechanics, and it left the door open for non-local hidden variables. Bell concluded: in a theory in which parameters are added to quantum mechanics to determine the results of individual measurements, without changing the statistical predictions, there must be a mechanism whereby the setting of one measuring device can influence the reading of another instrument, however remote. So, the signal involved must propagate instantaneously. Numerous experiments agree now with the predictions of this quantum mechanical theory, and show that differences between correlations that cannot be explained by local hidden variables. Thus the experimental results have been taken by many as refuting the concept of local realism as an explanation of the physical phenomena under test. Yet, if Bell’s conditions are correct, the results that agree with this quantum mechanical theory may indicate superluminal (faster-than-light) effects, in contradiction to the principle of local instantaneous effects [21] [30] (see also Section 5). It should be stressed that interpretation of EPR entanglement experimentation depends to a large extent on the interpretation of quantum physics one employs and also whether the wavelets are treated as particles or as waveforms; see an illustrative discussion in [36] .

4. History of Experimental EPR Realizations

EPR and Bell’s theorem have motivated researchers to improve the theory of quantum mechanics. Schrödinger pointed out that the EPR two-particle wave function does not represent the separable form but rather of the entangled form [37] . Experiments carried out to test Bell’s inequality during eight decades, therefore, have led to a re-examination of the concepts of quantum mechanics, and revealed the importance of the notion of entanglement and non-locality [22] . Most of these experiments employ photon pairs created via atomic transitions or using nonlinear optical techniques such as optical parametric amplification, or quantum spin values. When measured separately at stations A and B, along two arbitrarily chosen directions a and b, the correlation of the two results can be predicted, no matter how far apart spatially the measurements may be performed. Evidence for the EPR paradox has emerged in numerous experiments, including not only the correlations of single photon pairs, but the amplitudes and Stokes polarization observables of optical beams and pulses with macroscopic particle numbers [49] .

Among others: Clauser et al. found evidence against local hidden-variable theories by measuring linear polarization correlation of photons emitted in an atomic cascade of Calcium [38] . Aspect stated that a pair of entangled photons must be considered as a single, inseparable/entangled system, described by a global quantum state, which cannot be decomposed into two states, one for each photon [39] . Armstrong et al. presented experimental observations of multiparty EPR steering and of the genuine entanglement of three intense optical beams using optical networks and efficient detection. Hensen and Hanson et al. found an experimental loophole-free violation of a Bell inequality using entangled electron spins separated by 1.3 km [40] .

Many experiments have measured violation of the inferred Heisenberg uncertainty principle, and confirmed EPR-entanglement (see Appendix 1, and Appendix 2). It can be concluded therefore that experimental realizations of the EPR proposal provided ways to demonstrate a type of entanglement inextricably connected with quantum non-locality and always imply entanglement [22] . While early experiments used atomic cascades, later experiments used parametric down-conversion methods giving improved generation and detection properties [22] . As a result experiments with photons no longer suffer from the detection conditions and show an experimental system for which all main experimental loopholes have been surmounted, albeit mostly in separate experiments [41] [42] .

Of note, the observation of an EPR paradox for macroscopic objects at room temperature remains a question. The possibility of detecting an EPR paradox between two macroscopic atomic ensembles at room temperature, based on the experiments that have realized an entanglement between the ensembles has been examined [43] . Experiments have reported the entanglement of two spatially separated macroscopic atomic ensembles at room temperature [44] [45] . Read has summarized the measurements that show the degree of entanglement achieved in continuous variable experiments from 2000 till 2009 as depicted in Figure 2. The EPR paradox implying entanglement has been expressed at a “Degree of Inseparability” of <1 and more pronounced at <0.5 according to Duan’s criterion [46] .

However, an ingredient central to the EPR argument: causal separation of measurement events, is missing from the many experiments to date [22] [47] . It is considered that criteria of quantum coherence, electromagnetic wave coherence and quantum superposition are tools to find determinate values of a Quantum Equilibrium.

Quantum Equilibrium and Entangled States

Entangled photons can be considered as an inseparable system, and entanglement may be interpreted as a correlation between modes of the electromagnetic field. Entanglement between two light beams has been observed spanning an octave, or 1.5 octave or different parametric ratios in optical frequency [48] [49]

[50] . Three-color entanglement among the fundamental, second- and third-harmonic beams have been demonstrated by applying a tripartite entanglement criterion [48] . Multipartite Einstein-Podolsky-Rosen steering like tripartite entanglement with optical networks has been established [51] [52] [53] .

The concept of steering was introduced by Schrödinger in 1935 as a generalization of the EPR paradox for arbitrary pure bipartite entangled states. It is provided that steerable states are a strict subset of the entangled states, and a strict superset of the states that can exhibit Bell-nonlocality [54] . Increasing the number of measurement settings beyond two, by using geometries of Platonic solids, significantly increases the robustness of the EPR-steering phenomenon to noise [55] , and it is even possible to entangle the quadrature phase amplitudes of distinct fields [36] . It has been shown that the vertices of Platonic solids represent reasonable measurement choices for tests of Einstein-Podolsky-Rosen (EPR)-steering, that is, using iso-tropically entangled pairs of qubits. Such measurements are regularly spaced, and are a good feature for making EPR-steering inequalities easier to violate in the presence of experimental imperfections. However, such measurements are provably suboptimal [56] .

It is postulated by us that the Bohm’s Quantum Equilibrium has a typical determinate entangled configuration, of which the frequencies of the eigenvalues can be mathematically described by coherent eigenfrequency functions according to an adapted Pythagorean calculation. Bohm’s dynamics allow also a non-equilibrium, that are waves not in phase with the wave-functions and can be identified as non-coherent frequencies, able to disturb the proposed eigenfrequency functions. It is shown in the following that all physical experiments, carried out to show violation of Bell’s inequality during 50 years, can be precisely located at typical coherent frequencies according to Pythagorean rules as earlier shown for coherent states of living cells [1] [3] .

5. Quantum EM Equilibrium Frequencies Positioned at a Coherent Frequency Scale

EPR-measurements of about 40 different scientific groups in the period 1972-2017 have been analyzed, that demonstrated different types of entanglement connected with quantum non-locality (see literature references Figure 3 and Appendix 1 and Appendix 2). The EPR-measurements make use of different electromagnetic systems through exposures of discrete light, MHz and GHz-frequencies. To find a possible correlation between the different applied frequency modes it is proposed to normalize all the applied frequencies by ratios of 1:2ⁿ (n are integers) and to bring these modes in a scale within 1:2, making use of the fact that entanglement between beams has been observed by spanning an octave (1:2) and second-, and third-harmonics [48] [49] [50] [51] [57] [58] and see Appendix 3. By normalizing the frequencies at this manner discrete patterns of EPR-frequencies can be observed (see Figure 3). Interestingly, the particular 81 independent EPR-data at MHz-, GHz- and PHz-frequencies, fit precisely in

the proposed generalized coherent scale calculated according to an adapted Pythagorean scale calculation. The mean deviation of the applied frequency data, relative to the calculated different coherent frequencies amounts to maximally 0.65%, which is statistically relevant. It can be concluded that: 1) all analyzed EPR-measurements can be positioned at the normalized coherent frequency scale, of twelve scalars, 2) Multipartite Einstein-Podolsky-Rosen steering and tripartite entanglement with optical network are precisely divided over the typical calculated coherent frequencies (see experiments of Marshall, Scheidl, Hensen B., Feng, Armstrong, in Appendix 1).

6. Main Conclusions of the Semi-Harmonic Electromagnetic Frequency Pattern/EPR Literature Meta-Analyses

An analogy with the vision of Schrödinger has been found: when you perform a Schrödinger cat experiment, and observe the superposed system, than the outcome of the cat will either be alive or be dead, but never in between. All discrete EM frequencies of our GM-model for living organisms, show that cells are indeed either alive (sustaining coherent frequency patterns), or in contrast life deteriorating and/or life terminating (detrimental non-coherent frequency patterns) [1] [2] [3] , but in fact never in between. An extremely simple law of algorithmic coherent and non-coherent frequencies expresses this principle, as already known for Pythagorean musical scales. This law is only based on the knowledge how to divide ratios of 2:3 over ratios of 1:2. A causal separation also exists for the analyzed EPR-measurement events, of which the frequencies are also located at a determinate coherent frequency scale. In line with the life studies, the particular locations can be described by a coherent pattern of discrete frequencies according to an adapted Pythagorean scale calculation [1] [2] [3] . The found rule likely stands for locality as well as for non-locality events.

When the proposed algorithm of coherent frequencies is valid for both systems: 1) quantum entanglement of inanimate condensed matter, and 2) eigenfrequencies of living cells, than it may be concluded that living cells are coupled by quantum entanglement, and therefore may intrinsically show a behaviour of non-locality and entangled states.

7. Potential Physical Mechanism for Quantum Entanglement

7.1. De Broglie/Bohm Pilot-Wave Type of Steering from an Implicate Order and More Recent Modalities of the Theory

A likely candidate for the Bohmian implicate order, as a source for pilot wave activity, is the well-known stochastic zero-point energy field, in the framework of Stochastic Electrodynamics [15] [59] . The original de Broglie/Bohm interpretation of QM was later considered by several authors to be incomplete, since it lacks a back reaction of the particle on the wave state [60] [61] [62] [63] . This concept implies a symmetric/bidirectional flux of information between the zero-point energy and our physical world was also assumed in consciousness studies [64] [65] . The back-reaction theory also introduces an aspect of retro-causality in which future aspect of the wave function can, in a backward manner, influence the past aspect. This idea was as originally proposed by Wheeler, 1994 (delayed choice experiment, and later experimentally proven in many dedicated studies), and is also an aspect that is represented in the transactional interpretation of Cramer, 1988 and more recently proven in the so called weak stimulation experiments of Aharonov et al., 2010 [66] [67] [68] . Such a retro causal effect is compatible with classical symmetric QM and laws of nature, and was proposed to provide a solution for the realization of quantum entanglement between two or more wave/particles, without the necessity of information exchange at speeds exceeding the generally assumed maximal speed of light [59] [63] [68] .

According to Setterfield, 2017 In Quantum Electro-Dynamics, or QED physics, a sub-atomic particle’s position and momentum are claimed to be indeterminate until actually measured, according to the reigning Copenhagen interpretation [69] [70] . Furthermore, QED physics claims that the result of taking any physical measurement is to collapse the particle from its previous uncertainty into a state in which the measured property appears instantaneously. In Stochastic Electro-Dynamics, or SED physics, the established quantum uncertainty is caused through the battering of subatomic particles by the impacting electromagnetic fields and waves of the Zero Point Energy (ZPE) which are intrinsic to the vacuum. These impacting waves cause the particle to execute a “jitter-motion” (technically called the Zitterbewegung). For an electron, there are over 10²⁰ impacts per second by these ZPE waves.

Indeed, it has been demonstrated by SED physicists that many quantum phenomena can be described intuitively by classical physics when the action of the ZPE is added in [70] . Furthermore, as it was formulated in Planck’s second paper, published in 1911, Planck’s constant, h, may be not only a measure of the quantum uncertainty, but may be also a measure of the strength of the ZPE; the two are intimately connected. The situation with what has been called “quantum entanglement” may be another case where SED physics has an intuitive answer that has eluded QED physicists. Quantum entanglement has been described in this fashion:

“Quantum entanglement is a physical phenomenon that occurs when pairs or groups of subatomic particles are generated or interact in ways such that the quantum characteristics of each particle cannot be described independently―instead, a quantum state can be given for the system as a whole. Measurements of physical properties such as position, momentum, spin, polarization and so on that are performed on entangled particles are found to be appropriately correlated”.

The problem that arises for QED physics is that, before the measurement is made, the spin (or whatever property is being considered) is indefinite by the uncertainty principle. However, if a measurement is made on either of the entangled particles, it not only collapses the state of the particle being measured, but so (also instantaneously) does that of its companion particle, no matter how far away that particle has gone. The outcome of the measurement process is considered to be random, with each possibility having an equal probability. These concepts result in the problem of how one particle instantaneously “knows” what has happened to the other particle. SED physics may provide an answer to this dilemma: the entangled particles in question really implicitly will have this correlated property in advance of observation. This approach became known as the “hidden variables theory”. Furthermore, Bell’s treatment of the problem faced by the EPR approach is also insufficient because it, too, ignores the action of a real ZPE. Therefore, Bell’s inequality is not a sufficient reason to reject the proposition that entangled particles already possess their physical characteristics from the beginning.

In summary, then, it may be stated that particle entanglement is real and that measurement reveals that they have appropriately correlated quantities. The QED physicist claims that the particles properties do not start off correlated, but once a measurement is made on one particle, this forces the other particle to assume the correlated property no matter where that particle may be. This leads to the dilemma of particles signaling each other faster than light. Yet, the problem of particles signaling to each other faster than light is clearly eliminated by the SED approach. In other words: wave/particles by definition share information in the ZPE field and the interconnectedness is related to the wholeness of the entire quantum system, as being part of the supposed universal wave function. As mentioned above, the latter may act on an universal scale and instantaneously through the network of Einstein-Rosen bridges and entanglement can be viewed upon as a basic natural process [71] .

7.2. Entanglement Due to a Universal Wormhole Structure of Spacetime

We considered earlier that geodesic or toroidal nested geometries may play a role in electromagnetic communication in animate and inanimate systems [3] . It has been recently suggested that wormhole structures, inherently present in toroidal geometry, may be more optimal than regularly spaced Platonic geometries to realize a further robustness of EPR-steering [40] , and explain the instantaneous correlations observed on EPR-experimentation. It is even considered that spacetime itself should be explained on the basis of quantum entanglement [72] [73] [74] .

7.3. Relation with the Present GM-Model Hypothesis

It can be concluded that de Broglie/Bohm’s interpretation of quantum mechanics, that is nonlocal, causal, and based upon determinate values, is compatible with our proposed spectrum of determinate (discrete) and coherent electromagnetic frequencies. Also non-equilibrium values seem to exist in view of the observation that distinct frequencies are precisely located logarithmically just in between the coherent frequency bands, see Figure 1. The proposals of ‘t Hooft [34] [35] and Dolce [33] that the energy in quantum system should be envisioned in terms of a periodicity of the limit cycles and/or as cycling periodicity space time units, also provided a causal and deterministic framework in which entangled particles can be seen as being steered by hidden variables.

If Bohm’s Deterministic Quantum Equilibrium can be described by the proposed coherent frequency scale than different aspects for condensed matter should be valid:

- Condensed matter is able to perform at non-local conditions, if the emitted electromagnetic frequencies (from atmospheric conditions or, in our study, from experimental origin), obey to the pattern of the proposed coherent frequency scale. Due to the permanent presence of a plethora of electromagnetic wave interactions any wave/particle will be accompanied by a distinct steering pilot wave and the resulting superposition will at least result in a degree of mesotropic entanglement that is expressed throughout the universe.

- The most optimum interaction with an entangled non-local field might be expected if the emitted frequencies are precisely located at all of the 12 basic frequencies over the broad frequency range, but preferably in an entangled state. These will probably be more effective when these frequencies are at the Tera-Hertz range, in which also the photon and electron frequencies are found.

- The GM-model may be able to calculate both elementary particles masses and zero-point energies of elements.

8. Final Conclusion

The former papers discussed: 1) the mathematical structure for electromagnetic frequencies that may reflect pilot waves of Bohm’s Implicate Order, and 2) semi-harmonic scaling that enables calculation of masses of elementary particles of the Standard Model. The present concept based upon this novel biophysical principle, called by us the GM-model, describes a semi-harmonic electromagnetic guiding mechanism for animate and non-animate systems, and shows the influence of typical discrete electromagnetic frequencies on the promotion of entangled states in, so called, Einstein, Podolsky Rosen-experiments. It has been shown that frequencies of EPR-states can be precisely calculated. Therefore, it is also expected that the GM-model is able to calculate the zero-point energies of the elements. With regard to Quantum-Biology, the present principle could have implications for further studies in Quantum Mechanics and in Quantum-Biology, including brain function [75] [76] [77] . It follows from the present study that quantum entanglement may play a crucial role in the ecology of life systems and initiation of first life [13] [14] [36] [78] .

Conflicts of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Cite this paper

Geesink, H.J.H. and Meijer, D.K.F. (2018) A Semi-Harmonic Frequency Pattern Organizes Local and Non-Local States by Quantum Entanglement in both EPR-Studies and Life Systems. Journal of Modern Physics, 9, 898-924. https://doi.org/10.4236/jmp.2018.95056

References

Appendix 1. References of EPR-Measurements 1969-2017

1a) Clauser, J.F., Horne, M.A., Shimony A., Holt, R.A. (1969) Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett., 23, 880.

1b) Hensen, S.J., Clauser, J.F. (1972) Experimental Test of Local Hidden-Variable Theories. Phys. Rev. Lett., 28, 938.

2) Aspect, A., Dalibard, J., Roger, G. (1982) Experimental Test of Bell’s Inequalities Using Time-Varying Analyzers. Institut d’Optique Theomque et Appliquee, Qrsay Cedex, France.

3a) Fry, E.S., Walther, T., Li, S. (1995). Proposal for a loophole-free test of the Bell inequalities. Physics Department, Texas A&M University, College Station, Texas 77843.

3b) Walther, T., Fry, E.S. (1997) An Experimental Realization of Bohm’s Spin-1/2 Particle EPR Gedanken experiment. New Developments on Fundamental Problems in Quantum Physics, 431-439.

4) Shih, H., Alley, C.O. (1988) New type of Einstein-Podolsky-Rosen-Bohm Experiment using pairs of light quanta produced by optical parametric down conversion. Phys. rev. Lett., 61, 2921.

5) Weihs, G., Jennewein, T., Simon, C., Weinfurter, H., Zeilinger, A. (1988) Violation of Bell’s inequality under strict Einstein locality conditions. arXiv:quant-ph/9810080v1.

6) Kuzmich, A., Walmsley, I.A., Mandel, L. (1999) Violation of a Bell-type inequality in the homodyne measurement of light in an Einstein-Podolsky-Rosen state. Physical Review A, Volume 64, 063804.

7) Bouwmeester, D., Pan, J.W., Daniell, M., Weinfurter, H., Zeilinger, A. (1999) Observation of three-photon Greenberger―Horne―Zeilinger entanglement. Phys. Rev. Lett., 82, 1345-1349.

8) Silberhorn, C., Lam, P.K., Weiß, O., König, F., Korolkova, N., Leuchs, G. (2001) Generation of Continuous Variable Einstein-Podolsky-Rosen Entanglement via the Kerr Nonlinearity in an Optical Fiber. Physical Review Letters, Volume 86, Number 19.

9) Rowe, M.A., Kielpinski,D., Meyer, V., Sackett, C.A., Itano, W.M., Monroe, C., Wineland, J. (2001) Experimental violation of a Bell’s inequality with efficient detection. Nature, Vol. 409. https://www.nature.com/

10) Julsgaard, B., Kozhekin, A., Polzik, E.S. (2001) Experimental long-lived entanglement of two macroscopic objects. Nature, 413, 400-403.

11a) Bowen, W.P., Schnabel, R., Lam, P.K., Ralph, T.C. (2002) An experimental investigation of criteria for continuous variable entanglement. arXiv:quant-ph/0209001v1.

11b) Bowen, W.P., Treps, N., Buchler, B.C., Schnabel, R., Ralph, T.C., Bachor, H.A., Symul, T., Lam, P.K. (2002) Unity gain and non-unity gain quantum teleportation. Phys. Rev. A, 67, 032302.

11c) Bowen, W.P., Schnabel, R., Lam, P.K., Ralph, T.C. (2003) A characterization of continuous variable entanglement. Phys. Rev. Lett., 90, 043601.

12) Marshall, T.W., (2002) Nonlocality―The party may be over. arXiv:quant-ph/0203042 Freely accessible [quant-ph].

13) Feng, S., Pfister, O. (2003) Stable nondegenerate optical parametric oscillation at degenerate frequencies in Na:KTP. J. Opt. B: Quantum Semiclass. Opt., 5, 262-267.

14) Schnabel, R., Bowen, W.P., Treps, N., Buchler, B., Ralph, T.C., Lam, P.K., Bachor, H. (2003) Optical experiments beyond the quantum limit: Squeezing, entanglement, and teleportation. Optics and Spectroscopy, Volume 94, Issue 5, 651-665.

15) Josse, V., Dantan, A., Bramati, A., Pinard, M., Giacbino, E. (2004) Entanglement and squeezing in a two-mode system: theory and experiment. Phys. Rev. Lett., 92, 123601.

16) Villar, S., Cruz, L.S., Cassemiro, K.N., Martinelli, M., Nussenzveig, P. (2005) Generation of Bright Two-Color Continuous Variable Entanglement. Physical review letters, 95(24), 243603.

17) Huntington, E.H., Milford, G.N., Robilliard, C. (2005) Coherent analysis of quantum optical sideband modes. arXiv:quant-ph/0504022 v1 5 Apr.

18a) Wenger, J., Hafezi, M., Grosshans, F., Tualle-Brouri, R., Grangier, P. (2003) Phys. Rev. A, 67, 012105.

18b) Wenger, J., Ourjoumtsev, A., Tualle-Brouri, R., Grangier, P. (2005) Non-gaussian statistics from individual pulses of squeezed light. Eur. Phys. J. D, 32, 391.

19) Laurat, L., Longchambon, L., Fabre, C., Coudreau, T. (2005) Experimental investigation of amplitude and phase quantum correlations in a type II optical parametric oscillator above threshold: from nondegenerate to degenerate operation. Opt. Lett., 30, 1177-1179.

20) Walther, P., Resch, K.J., Rudolph, T., Schenck, E., Weinfurter, H., Vedral, V., Aspelmeyer, M., Zeilinger A. (2005) Experimental One-Way Quantum Computing. Nature, 434, 169-176.

21) Yoshino, K., Aoki T., Furusawa A. (2007) Appl. Phys. Lett., 90, 041111.

22) Scheidl, T., Ursin, R., Kofler, J., Ramelow, S., Xiao-Song M., Herbst, T., Ratschbacher, L., Fedrizzi, A., Langford, N.K., Jennewein, T., Zeilinger, A. (2010) Violation of local realism with freedom of choice. PNAS, Vol. 10, No. 46, 19708-19713.

23) Keller, G., D’Auria, V., Treps, N., Coudreau, T., Laurat, J., Fabre, C. (2008) Experimental demonstration of frequency-degenerate bright EPR beams with a self-phase-locked OPO. June/Vol. 16, No. 13/OPTICS EXPRESS 9351.

24) Boyer, V.A M., Pooser, M.R., Lett, P. (2008) Science, 321, 544.

25) Grosse, N.B.S., Mehmet, A.M., Schnabel, R., Symul, T., Lam, P.K. (2008) Observation of entanglement between two light beams spanning an octave in optical frequency. Phys Rev Lett. Jun 20, 100(24), 243601.

26) Reid, M.D., Drummond, P.D., Bowen, P., Cavalcanti, E.G., Lam, P.K., Bachor, H.A., Andersen, U.L., Leuchs, G. (nnnn) Colloquium: The Einstein-Podolsky-Rosen paradox: From concepts to applications. Rev. Mod.

27) Li, Y., Guo, X., Ba, I Z., Liu, C. (2010) View Affiliations. Appl. Phys. Lett., 97, 031107. DOI: 10.1063/1.3467045

28) Li, C.F., Xu J.S., Xu, X.Y., Li, K., Guo, G.C. (2011) Experimental investigation of the entanglement assisted entropic uncertainty principle. Nature Physics, 7, 752-756.

29) Buono, D., Nocerino, G., Porzio, A., Solimeno, S. (2012) Experimental analysis of decoherence in continuous-variable bipartite systems. Phys. Rev. A, 86, 042308.

30) Prevedel, R., Lu, Y., Matthews, W., Kaltenbaek, R., Resch, K.J. (2011) Entanglement-Enhanced Classical Communication over a Noisy Classical Channel. arXiv:1010.2566v2 [quant-ph] 31 March.

31) Christensen et al. (2013), Detection-Loophole-Free Test of Quantum Nonlocality, and Applications. arXiv:1306.5772v2 [quant-ph] 26 Sep.

32) Zhao, T.M., Zhang, H., Yang, J., Sang, Z.R., Jiang, X., Bao, X.H., Pan, J.W. (2014) Entangling Different-Color Photons via Time-Resolved Measurement and Active Feed Forward. Phys. Rev. Lett., 112, 103602.

33) Moreau, P.A., Mougin-Sisini, J., Devaux, F., Lantz, E. (2014) Realization of the purely spatial Einstein-Podolsky-Rosen paradox in full-field images of spontaneous parametric down conversion. HAL Id: hal-00949144.

34) Fedrizzi, A. (2014) Viewpoint Entangling Photons with Mismatched Colors Physics, 7, 25.

35) Sanz, A.S. (2014) Particles, waves and trajectories: 210 years after Young’s experiment. EmQM13: Emergent Quantum Mechanics. IOP Publishing Journal of Physics: Conference Series 504, 12028.

36a) Giustina, M. et al. (2013) Bell violation using entangled photons without the fair-sampling assumption. Nature, 497, 227-230.

36b) Giustina M., Zeilinger A., et al. (2015) Significant-Loophole-Free Test of Bell’s Theorem with Entangled Photons. Published by the American Physical Society.

37) Lantz, E., Denis, S., Moreau, P.A., Devaux, F. (2015) Einstein-Podolsky-Rosen paradox in single pairs of images. arXiv:1506.01615 [quant-ph].

38) Liu, W., Wang, N., Li, L., Lia, Y. (2015) Quantum frequency up-conversion of continuous variable entangled states. Applied Physics Letters, 107, 231109.

39) Morris, P.A., Aspden, R.S., Bell, J.E.C., Boyd, R.W., Padgett, M. (2015) Imaging with a small number of photons. Nature Communications, 6, Article Number: 5913.

40) Armstrong, S., Wang, M., The, R.Y., Gong, Q., He, Q., Janousek, J., Bachor, H.A., Reid, M.D., Lam, P.K. (2015) Multipartite Einstein-Podolsky-Rosen steering and genuine tripartite entanglement with optical networks. Nature Physics, Vol. 11. http://www.nature.com/naturephysics

41) Hensen, B., Hanson R. et al. (2015) Loophole-free Bell Inequality Violation Using Electron Spins Separated by 1.3 Kilometres. Nature, 526, 682.

42) Tian, L., Li, S., Yuan, H., Wang, H. (2016) Generation of Narrow-Band Polarization-Entangled Photon Pairs at a Rubidium D1 Line. J. Phys. Soc. Jpn., 85, 124403.

43 Parigi, V. (2017) Multimode quantum optics group, Quantum multimode resources based on optical frequency combs and simulation of complex quantum network, lecture, QuProCSII.

44) Cai, Y., Roslund, J., Ferrini, G., Arzani, F., Xu, X., Fabre, C., Treps, N. (2017). Multimode entanglement in reconfigurable graph states using optical frequency combs. Nat Commun., 8, 15645.

45) Yin, J., Pan J. W. et al. (2017) Satellite-based entanglement distribution over 1200 kilometers. Yin Y. et al. Science, Vol. 356, Issue 6343, 1140-1144. DOI: 10.1126/science.aan3211

Appendix 2. Table Applied Frequencies of EPR-Measurements 1969-2017

1a, b, c. 227.5 nm, 551.3 nm, 422.7 nm

2. 551.3 nm, 422.7nm, 50 MHz

3a. 253.7 nm, 3b. 532 nm, 3c. 710 nm

4. 532 nm

5. 670 nm, 351 nm, 702 nm, 10 MHz, 30 MHz, 10 fs

6. 405 nm, 80 MHz

7. 394 nm, 200 fs

8. 376.3 nm, 163 MHz

9. 626 nm

10. 426 nm, 447 nm, 700 MHz

11a, b, c. 532 nm

12. 702 nm, 600 nm, 700 nm, 400 nm, 422.5 nm

13. 532 nm, 150 KHz, 3 MHz

14. 532 nm

15. 5 MHz

16. 532 nm

17. 532 nm

18a, b. 425 nm, 150 fs, 790 kHz

19. 532 nm

20. 395 nm

21. 473 nm

22. 405 nm, 3.4 × 10⁷ Hz, 2.4 GHz, 30 MHz

23. 532 nm, 20 MHz

24. 0.5 MHz, 6 GHz

25. 532 nm, 1064 nm

26. 532 nm

27. 526.5 nm, 0.8 mu, 1.5 μm

28. 400 nm, 76 MHz

29. 532 nm, 1064 nm

30. 404 nm, 200 kHz

31. 710 nm, 120 MHz

32. 397 nm 795, 40 MHz, 80 MHz

33. 710 nm

34 795 nm, 40 or 80 MHz

35. 471.5 nm

36a, b. 405 nm

37. 710 nm

38. 403 nm, 1518 nm

39. 710.1 nm

40. 532 nm

41. 637 nm, 100 MHz, 2.874 GHz

42. 397.5 nm

43. 400 nm, 80 MHz

44. 76 MHz, 120 fs pulses

45a, b, c. 405 nm, 532 nm, 671 nm

Appendix 3. Table Calculated Algorithmic Reference Frequencies of EPR-Measurements 1969-2017

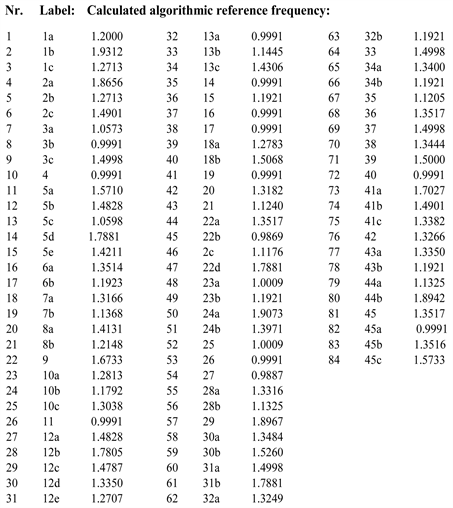
Appendix 4. Calculated Examples of Coherent Frequencies from Sub Hertz Till PHz

Appendix 5. Generalized Scale of Coherent Frequencies

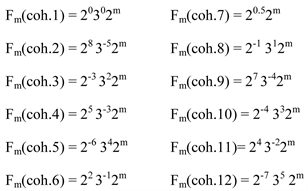
Appendix 6. Generalized Scale for Non-Coherent Frequencies

NOTES

“The observed physical and biological world of becoming is a reflection of a mathematical world of being”