ABSTRACT

Throughout scientific research, the state space reconstruction that embeds a non-linear time series is the first and necessary step for characterizing and predicting the behavior of a complex system. This requires to choose appropriate values of time delay T and embedding dimension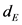. Three methods are applied and discussed on nonlinear time series provided by the Rössler attractor equations set: Cao’s method, the C-C method developed by Kim et al. and the C-C-1 method developed by Cai et al. A way to fix a parameter necessary to implement the last method is given. Focus has been put on small size and/or noisy time series. The reconstruction quality is measured by using a criterion based on the transformation smoothness.

Keywords:

Phase Space Reconstruction, Embedding Window, Rössler System, Time Series, Correlation Integral, Delay Time

1. Introduction

In many fields of science and industry, complex systems are studied through temporal time series of scalar observations of a k dimensional dynamical system [1] [2] [3] [4] [5] . In most cases, the state space dimension and the system of equations that define the system evolution and behavior in the state space are unknown. Each value in a time series results from the interaction of the state variables in the state space. The main purpose of time series analysis is to learn about the dynamics behind some time ordered measurement data. To investigate an experimental kth order dynamical system from a scalar time series, it is necessary to reconstruct a state space by using time delay or time derivative coordinates. The reconstructed trajectory is expected to have the same characteristics than the trajectory embedded in the original phase space. It can be proved through Taken’s theorem that the unstable periodic orbits of a strange attractor could be recovered in an embedded state space whenever the time series is long enough with no noise [1] [2] [5] [6] [7] [8] [9] . In that case, the embedding dimension 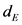and the time delay T [1] [2] [3] [10] [11] are not correlated and can be selected independently [7] [8] [9] . In the real world, time series are not infinitely long and could be hardly noisy. In that case 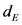and T are correlated and an alternative approach used in the literature is to determine the time window length 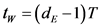which is the entire time spanned by the embedding vectors [7] [8] [9] . Once 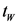is determined, the time delay T should be chosen so that the serial correlation of the 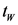time subseries should be minimum [7] [8] . As the essence of serial correlation is to see how sequential observations in a time series affect each other, Brock, Dechert and Scheinkman have developed a new statistic named “BDS statistic” able to test if a given data set is independently and identically distributed [12] [13] . The BDS statistic is based on the correlation integral and Brock has shown that the correlation integral behaves like the characteristic function of a time series through the fact that if the time series arises from several independent random variables, the correlation integral is the product of the correlation integrals of sub time series components. In that sense, the BDS statistic can be interpreted as the serial correlation of a nonlinear time series. State space reconstruction is necessary before developing forecasting methods and, as the quality of state space reconstruction affects significantly the accuracy in time series forecasting, the scope of this paper is threefold: i ) to review test and compare, in terms of quality, three methods used for selecting state space reconstruction parameters (time delay, embedding dimension) from a nonlinear time series provided by the Rössler attractor equations set; ii) to apply these methods to small size time series and test their robustness to noise with the objective to use them for experimental data; iii) to qualify these methods by defining a criterion able to measure the quality of the state space reconstruction.

In this work, a pseudo experimental approach is considered. The equations describing the Rössler attractor are solved numerically. The numerical values obtained are assumed to be measurements. We start from a scalar time series 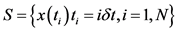of N observations of the Rössler x variable with the 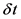sampling rate that is the shortest time between two measurements. The method of delays is used to embed the time series S into a set of points of a 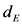dimensional space where T is the delay time given by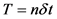, 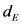the embedding dimension and , the number of embedded points. The reconstructed state space must be topologically equivalent to the original one, the selection of optimal values for T and 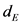are very important and affect the quality of the reconstruction. Through the large number of publications dealing with this subject, there are two main approaches of selecting and T. The first approach consists in selecting 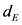and T independently and is generally used in the case of sufficiently long noise free time series [7] [8] [9] [14] [15] . When time series are limited or contaminated by noise, the theorem of Takens is silent and the delay time T is observed to vary with the embedding dimension. In this case, as an irrelevant partnership between T and 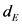could affect the equivalence between the reconstructed space and the original one, another approach, based on the delay time window, selection, is used for the state space reconstruction [7] [8] [16] [17] .

This article is structured around three sections, this work, can be considered as the preliminary step to the time series forecasting methods development, the first section is devoted to the calculation of the maximum Lyapunov exponent and the Lyapunov dimension from time series obtained by integrating numerically the Rössler differential equations set. The second section is focused on the state space reconstruction parameters selection. The main idea is to subdivide the original time series S into p sub-series, each of them representing an embedded point in a dimensional space. For an optimal choice of the state space reconstruction parameters, all the embedded points form a sufficiently representative trajectory of the attractor considered.

Three methods able to select the embedding dimension and the time delay T are discussed in this section. First Cao’s method [14] is applied on sufficiently long noise free time series (≈32,000 values) and shows some drawbacks when applied to smaller size and/or noisy time series (≈4000 values). Aiming at improving these drawbacks, two other methods based on the time delay window selection are discussed: the C-C method developed by Kim et al. [7] and the C-C-1 method developed by Cai et al. [8] . These two methods are described and results obtained are compared and discussed. In the framework of the C-C-1 method, a criterion that fix the number of subseries composing the initial time series S, is suggested. The sensitivity to noise of the different techniques addressed in this section are analyzed and results obtained are discussed. The third and last section is dedicated to the measure of the reconstruction quality. In the case of long free noise time series, as Takens embedding theorem ensures a topological equivalence between the original state space and the reconstructed one, the quality of the reconstruction is measured through the conservation of invariants such as the maximum Lyapunov exponent and the correlation dimension. In the case of limited noise free data set, we have used a technic based on a statistic approach similar to the Rul’kov et al. test [18] , by calculating the quotient F of two ratios. One ratio is the nearest-neighbor distance on the original state space to the distance on the corresponding points on the reconstructed state space. The other ratio is the nearest-neighbor distance on the reconstructed state space to the distance between the corresponding points on the original state space. For a smooth mapping between the time series, the quotient of these two ratios should be close to unity [18] [19] .

This paper also constitutes a sort of set-up in order to become familiar with these different techniques before applying them to real experimental data.

2. Calculation of Lyapunov Exponents and Lyapunov Dimension for the Rössler Attractor

The dynamical system of interest in this first part consists of the following three coupled differential equations [4] [20] [21] [22]

(1)

where a, b and c have constant values. These equations have a chaotic attractor which is displayed in Figure 1 which was obtained from a simple numerical integrator.

The Rössler attractor is largely a product of the interaction between an attracting direction and a repelling one. The calculated trajectory starts close to a fixed point, the linear terms of the two first equations create oscillations in the variables x and y. These oscillations are amplified, which results into a spiraling-out motion. The motion in x and y is then coupled to the z variable ruled by the third equation, which contains the nonlinear term and which induces the reinjection back to the beginning of the spiraling-out motion. A very complex

dynamic arises.

When chaos takes place, one can observe a great sensitivity of the motion to small changes in initial conditions. Two closely neighboring trajectories diverge exponentially. Their rate of divergence is constant, and a plateau is obtained when determining the Lyapunov exponent numerically. When a = 0.2 and b = 0.4, chaos appears when c has a sufficiently high value. This is shown by calculating maximum Lyapunov exponents using Benettin’s method [3] [20] [21] [23] [24] for different trajectories considering different values of parameter c.

Figure 2 shows that chaos takes place when c is between 5 and 5.2.

Then, considering a = 0.2, b = 0.4 and c = 5.7, a positive maximum Lyapunov exponent for this trajectory is calculated by using Benettin’s method. Two trajectories with two very close initial conditions were considered and they were renormalized for every fixed time interval Δτ. The following value was found:

The transition from simple to strange attractor proceeds via a sequence of period-doubling bifurcations [20] .

Then, considering the parameters defining the Rossler attractor shown in Figure 1 (a = 0.2, b = 0.4 and c = 5.7), the Lyapunov exponents spectrum is calculated. The algorithm employed was proposed Wolf et al. [25] . The numerical results are shown in Figure 3.

The values of the three Lyapunov exponents are

(2)

as expected. On average, is the expansion rate of the stretching process of the attractor, and is the reduction rate of the folding process.

The number of non-negative Lyapunov exponents, d = 2, allows us to identify the dimension of the attractor [26] . We are going to show that its fractal dimension is a little bit greater.

The Lyapunov dimension is related to the Lyapunov spectrum by [5] [25] [26] [27]

(3)

where j is defined by the conditions and. Thus

(4)

which means that the attractor is close to a plane surface. The fractal dimension gives a lower bound on the number of variables needed to model the dynamics of the attractor.

3. Time Delay Reconstruction of the State Space by Sampling a Coordinate of the Rössler Attractor

3.1. Formulation of the Problem

Let us move to a pseudo experimental approach. It is assumed that we only have a single sequence of measurements obtained at different times. We seek a hidden determinism in our experimental data. Here, the “experimental results” are given by a numerical integration of Equation (1). In this section, we just try the reconstruction method provided by the tool box CDA22 [1] .

It is assumed that only the x-components of the vector, which gives the state of the system, is measured or calculated. Then, , where G is a scalar function of the state vector. We define what is called delay coordinate vectors such as [3] [4] [6] [7] [8]

(5)

where is here a simple parameter and T is the time delay.

Packard et al. [4] [6] have shown that starting from the time series (5), one may reconstruct the trajectory of the attractor in a -dimensional embedding space by means of vectors

(6)

with, where j is an integer and is the minimum sampling time. Time is the sampling interval between the first components of successive vectors. Based on (6) and assuming the time window spanned by the p embedded points is included in the time window spanned by the N values of the initial time series, it holds that. If where n is an integer, it may be written that is:. Thereafter, we will set j = 1 and we shall have

(7)

3.2. Considerations on the Minimum Embedding Dimension

The space reconstruction requires to select values of the reconstructed space dimension and the time delay. The embedding theorem [6] [9] [10] [28] tells us that the following sufficient but not necessary condition must be verified

, (8)

where is the box-counting dimension of the attractor. Considering that [2] , the condition (8) is satisfied when

(9)

that is

(10)

To verify the relevance of this condition, the reconstruction was achieved considering several values of and using the CDA22 tool box [1] . Let x(t) be a one-dimensional data set evaluated at equal increments of the variable t. The values of x(t) were obtained by solving numerically Equation (1) using a fourth order Runge-Kutta scheme. These values of x play the role of experimental measurements. Using CDA22 tool box the correlation dimension of the Rössler attractor was calculated for. It is reminded here that where is the sampling rate, we chose and found . Then, was calculated for different values of. First the same values of and n were considered. The results are shown in Figure 4 Very different values of and n were also considered, we chose and. Figure 4 shows that the two curves merge.

Figure 4 shows the curves versus obtained with two set of parameters. The full line is obtained with and, squares are ob-

tained with and. When, squares are very closed to the full line curve and the plateau seen in corroborates condition (10) which means that, for the long limited noise free data sequence considered here, Taken’s theorem is satisfied. The correlation dimension becomes an invariant on the attractor when the embedding dimension used for the computation increases. Then, the optimal embedding dimension is reached [11] . Still, Figure 4 shows that is a sufficient but not necessary condition, would be quite suitable. The typical problem with this way to determine the embedding dimension is that it is very time-consuming for computation.

Figure 4 also shows that the results obtained for are not, at least in this range of values, sensitive to n and consequently to the time delay T. Because the initial data set contains about 32,000 values and is noise-free, results obtained are in good agreement with Takens [6] [7] [9] . In this case, the existence of a diffeomorphism between the original attractor and the reconstructed image exists for almost any choice of time delay and a sufficiently high embedding dimension.

It is known that [1] , then, as, one must have [29] which in good agreement with our numerical results.

3.3. Cao’s Method for Determining the Embedding Dimension

The optimal embedding dimension has also been calculated by using Cao’s algorithm which is much less time-consuming [9] [14] . According to the IIIa paragraph notations and (7), Cao defines as a function of (with) the i^th reconstructed vector and the embedding dimension, is written as

(11)

where denotes the sup-norm, i.e.,

and is the i^th reconstructed vector in the dimensional reconstructed space. Subscript refers to the which is the nearest neighbor of in the dimensional reconstructed space. Integer depends on i and. If is qualified as an embedding dimension by the embedding theorem [1] [2] [3] [6] [27] , then any two points which stay close in a dimensional reconstructed space will be still close in a dimensional reconstructed space. Such a pair of points are called true neighbors, otherwise, they are called false neighbors. To qualify two points to be false neighbors, must be larger than a threshold value which depends on the i state point chosen. To avoid this problem, the quantity is defined as the mean value of all’s

(12)

with T =, so that is only dependent on the embedding dimension and the time delay. To investigate the variation of E between and, we define as. If stops changing when, then is the minimum embedding dimension we are looking for. When meaningful predictions from chaotic time sequence cannot be made, data appears to come from a random system. Considering that provided by a random set of numbers will never attain a saturation value as increases, it is necessary to distinguish deterministic chaotic from random data sequences. In most cases, it is difficult to resolve whether is slowly increasing or has stop changing if is sufficiently large. In fact, since available observed data samples are limited in number, it may happen that stops changing at some value although the time series is random. To solve this problem Cao [14] has suggested to consider the quantity which is useful to make distinction between deterministic signals from stochastic ones. Let us consider the following quantity

(13)

where the meaning of is the same as above. As for, to study the variations, an quantity is defined as . For random data, since the future values are independent of the past values, will equal unity for any. In the case of deterministic data is certainly related to and cannot be a constant for all. In other words, there must exist some values such that. Cao recommends to calculate both and for determining the minimum embedding dimension of a scalar time series. Figure 5 shows results obtained with Cao’s method applied to an about 32,000-data sequence by using CDA22 tool box.

Figure 5 shows that is related to and is not a constant for all

. This is in good agreement with the fact that the data used are deterministic. When n = 15, the minimum embedding dimension is. When n = 1, the same value is found for. This means that, when enough points are considered and when no noise is considered, the minimum value for is almost independent of T.

Then, Cao’s algorithm has been applied on a much smaller data sequence of about 4000 values, and were calculated. It was shown that can be different from zero in all the cases. It confirms the deterministic character of the data. It also shows that when n = 50 or when n = 10, the minimum embedding dimension is close to. A saturation value as increases is more difficult to discern when n = 1. Still, we can conclude that for this relatively small number of data, the minimum embedding dimension is still almost independent of n.

Cao’s method has been applied then to the 4000 values data-sequence with noise added. Figure 6 show results obtained when a white Gaussian noise with variance one is added to the 4000 values data-sequence.

In Figure 6, when n = 50 and n = 10, can be clearly different from unity, reaches a constant value for about the same value of:. For n = 1, remains close to unity, our data do not appear to be deterministic.

Then, a white Gaussian noise with variance five was added. Figure 7 show that a high value of n is necessary to determine a minimum embedding dimension. The following values for and were found

In this case is clearly different from a constant only for n = 100.

In summary, it was shown that for noise-free data of very long length, the reconstruction is valid for any time delay as far as the embedding dimension is high enough. When going to small number noisy data samples, the time delay used to determine the minimum embedding dimension cannot have any value.

3.4. Simultaneous Determination of the Embedding Dimension and Time Delay by Using the C-C Method

The Cao’s method [14] , used to determine the optimal embedding dimension , has shown that for a sufficiently long noise free data set, the time delay T and the minimum embedding dimension are almost independent and the delay time T can be set arbitrarily. However, when white Gaussian noise is added, T varies with and an irrelevant partnership between T and will directly impact the equivalence between the original state space and the reconstructed one. Moreover, in the real world, measurements data set are finite and noisy, and in this case, a more useful quantity to estimate the embedding dimension is the delay time window which is the entire time spanned by the vectors. Martinerie et al. [17] have shown that is an essential factor for estimating the correlation dimension. In their paper, they have demonstrated that first, determines the correlation integral characteristics and second, the correlation integral is very sensitive to the values. H.S. Kim et al. [7] and Wei-Dong Cai et al. [8] have developed a method which uses the correlation integral and is based on a statistic similar to the BDS statistic that Brock et al. [12] [13] used for their development for distinguishing random time series from chaotic or nonlinear stochastic time series. By using the notations of Equations ((6) and (7)), the BDS statistic applied to the time series writes [7] [8]

(14)

where is the correlation integral

(15)

r is a search radius and H is the Heaviside function: H(a) = 0 if a < 0 and H(a)=1 if a ³0. N is still the size of the data set, n is the index lag, is the number of embedded points in the dimensional space and still denotes the sup-norm. measures the fraction of pair of points whose sup-norm distance is not greater than r. Brock et al. have proved that if the stochastic process is independent and identically distributed (iid) then, for all and r. The density of points in a hypersphere of radius r scales like. It means that the correlation integral of the process behaves like the one of an independent random variables product which is the product of the correlation integral of each random variable. This leads to interpret the statistic S as a dimensionless quantity which highlights determinism. A significant nonzero value of S is evidence for determinism in the time series. The technique developed by Kim et al. called the C-C method consists in subdividing the time series into n disjoint time series each one of N/n values. One has

(16)

The average of the statistical quantity given by Equation (14) is defined as

(17)

when, can be rewritten in the following way

(18)

The locally optimal times may be either the zero crossing of for all r or the times at which shows the least variation with r, since this indicates a nearly uniform distribution of points. From several representative values, we define the quantity

(19)

which measures the variations of with r.

For data set with finite sample sizes N, appropriate choices for, r and n should be in agreement with the BDS statistic. For example, when applied to a data set with a sequence of about 4000 values, varies in the range [2, 7], n varies in the range [1, 200] and varies in the range with k = 1, 2, 3, 4 and is the standard deviation of the time series. We then define the average of quantities given by Equations ((17) and (19)).

(20)

and

(21)

As locally optimal times are either zero crossing of or times at which shows the least variation with r, we look for the first zero crossing of or the first local minimum of to find the optimal times for data independence which will gives T. The optimal time is the time for which and are both closest to zero. As the two quantities and may not be minimum at the same time (see Figure 8), we may look at the minimum of the quantity [7] [8]

(22)

which gives the delay time window. T is in a sense the minimum value of, it is determined as the minimum of the curve versus n running from 1 to 200. The C-C method has been programmed in R by using the packages “nonlinearTseries and tseriesChaos”. An organigram of the C-C method used in this work is presented in Appendix 1 and the results obtained on low size data sequence of about 4000 values are presented in Figure 8 & Figure 9.

The first local minimum of (Figure 8) occurs when n = 12 and represents the optimal delay time T.

The minimum of (Figure 9) occurs when n = 157 which is the optimal time embedding window. Then, the embedding dimension is given by, where the function int() represents the integer part.

White Gaussian noises with different variances σ (σ = 1, σ = 5, σ = 10) has been added to the noise free original signal of 4000 data sequence and the C-C method has been applied to the time series where x is the

noise free original signal, is a white Gaussian noise with zero mean and a variance σ, α is the strength of the noise and represents the level of noise in percentage (20%, 30%, 50%, 70%, 100%). The C-C method is performed for each σ and α values and the variations of T and compared to the reference values obtained from the original 4000 noise free data set, are shown in Table 1. The σ and α values ensuring the stability of the C-C method when applied to noisy data set are those for which.

The parameter α is linked to the signal to noise ratio SNR which can be defined as where is the mean value of the noisy data sequence and is the standard deviation of the noisy part of that is. As the standard deviation of may be written with and, one has:

(23)

then, the C-C method should be stable against the noise for values of α such as.

In Table 1, we observe that for σ = 1, the C-C method is stable against the noise when. For σ = 5, it is stable when, and for σ = 10, it is stable when.

In summary, the C-C method is a relatively simple method easy to implement that can be used for relatively small data set to determine both the time delay T and the time delay window. This method is robust against low and intermediate noise level.

3.5. An Optimization of the C-C Method

In their paper, W.D Cai et al. [8] pointed out some problems that limit to the C-C method. The first one is that there are local minimal points whose values are very close to the minimum of and they disturb the minimum estimation (see Figure 9). The second one is that shows high frequencies oscillations, increasing with n, that can affect the estimation of the first local minimum of (see Figure 8). Based on these remarks, W.D. Cai et al. have developed in their paper [8] a new method called C-C-1 different from the C-C method calculating with another average method.

Starting from the N values initial data set and according to (7), the number of the embedded points calculated from the delay time T in the dimensional reconstructed space is. A positive integer q independent of the delay time T is selected as a constant, to subdivide the embedded points series into q subseries, each with embedded points where the “int” function means integer part.

(24)

as each component is composed of components, Equation (24) can be rewritten as

(25)

Kim et al. have shown in their paper [7] that, when using the BDS statistic on time series, the sample data size N should be appropriate relatively to the values of, r and n. They have shown that for finite time series of size N ³ 500 the statistic represents the true correlation of the time series. The parameter q can be adjusted so that the size of the time subseries will not be too short.

The average of the statistical quantity given by Equation (14) is defined as follows:

(26)

The definitions of are given formally by Equations (20)-(22). The first local minimum of is the optimal delay time T.

If we define the mean orbital period P of a chaotic system as the mean period generated by the oscillations of the chaotic attractor in the phase space orbits, an optimal value for would coincide with the first period of the N values initial time series S. Cai has shown in his paper that with the new statistical quantity average he defines in (26), the peak values of corresponds to the orbital period P values of S and all the points that bring this values are the minima of.

Therefore, a new quantity is defined by

(27)

By looking for the minimum of, we estimate the optimal time window corresponding both to the minima of and to the first period P of the initial N values time series S.

The C-C-1 method has been programmed in R language by using the same packages as with the C-C method. An organigram of the C-C-1 method is presented in Appendix 2 and results obtained the 4000-values data sequence with q = 19 are shown in Figure 10.

High frequencies oscillations occurring when applying the C-C method (red dashed line) have disappeared in the C-C-1 method (black solid line) (see Figure 10). In Figure 10, the first local minimum occurs when n = 10 while it

was n = 12 for the C-C method. n = 10 represents the optimal delay time T.

Figure 10 shows that the estimate of the optimal delay time T in the C-C-1 method (n = 10) is quite the same as with the C-C method (n = 12). The first local minimum of coincide with the first period P of the chaotic time series S, and gives the optimal delay time window. The graph of in Figure 11 (black solid line) enables to distinguish clearly the first local minimum from the other local minima. The estimate of the optimal delay time window occurs for n = 33 when is minimum, or with the first peak value of [7] and is different from the optimal delay time window estimated in the C-C method. The optimal embedding dimension is given by and is closer to the estimation given by the Cao’s method (paragraph III c) and agrees with the results presented in paragraph IIIb.

An optimization of the C-C-1 method should be to define a criterion for the optimal selection of the q parameter value. Based on the results obtained from the C-C method, a criterion is suggested here to select optimally the q parameter value. We define first the quantity

(28)

where is given by Equation (19) and. The op-

timal choice of the q parameter value should coincide with the first value of n at which shows the least variation with. This requires to define the quantity

(29)

Figure 12 shows the evolution of Q(n) as a function of n.

As the value of the q parameter should be chosen so that the time subseries will not be too short. The optimal q value may be chosen as the first value of n for which shows a minimum variation with, that is q = 19. An organigram for obtaining the graph of the variable Q as a function of

n is presented in Appendix 3.

The C-C-1 method has been applied to the time series where is the noise free original signal obtained from the about 4000 values data set, is a white Gaussian noise with zero mean and a variance σ (σ = 1, 5, 10), α is the strength of the noise and represents the level of noise in percentage (20%, 30%, 50%, 70%, 100%). T and variations with the different values of σ and α are shown in Table 2.

We observe that the C-C-1 method gives stable results for σ = 1, for σ = 5 since, and for σ = 10 since.

In conclusion, the C-C-1 method is an improvement of the C-C method. The original time series is subdivided by setting a parameter q which is independent of the time delay T. Tests performed on this method show that it gives more reliable and stable estimates of the optimal delay time T and the optimal time delay window. Tests show also the robustness of this method in presence of noise as the embedding dimension remains equal when noise free data set is degraded with white Gaussian noises with variances respectively equal to 1, 5, 10.

4. Reconstruction Qualification

How can we measure the quality of a reconstruction? Time-delay embedding provides a diffeomorphic representation of the original state space. This means that the mapping between the original and the reconstructed state space is a smooth one. As the optimality of the reconstruction is based on minimizing the distortion of the original attractor when applying the reconstruction map [30] , an appropriate measure of the quality of a reconstruction would be to measure the smoothness of the transformation between the original and the reconstructed space [18] . Once such a transformation is achieved, a good evaluation of invariants such as the Lyapunov exponent and the fractal dimensions of the attractors is required.

In the case of a large size of noise-free data (about 32,000 values), Takens time-delay embedding ensures a topological equivalence between the original and reconstructed space and a way to assess this equivalence is to check whether the fractal dimensions of the attractors are preserved [9] [18] [31] . The maximum Lyapunov exponent was calculated using the CDA22 tool box, we found for, and. The value found when using Benettin’s method in paragraph II is in the range defined by this error bar. Considering the same parameters, the correlation dimension, , was also calculated with CDA22. We found which is very close to the Lyapunov dimension, , calculated directly by integrating Equation (1).

Moreover, considering for, and, the correlation dimension calculated with CDA22, , was found again to be very close to the Lyapunov dimension,. In this case the Lyapunov exponent was not calculated with enough accuracy because the number of data which can be used with CDA22 is limited. In each case, at least one invariant is conserved. Then, one can conclude that the reconstruction was achieved satisfactorily [18] [32] .

In the case of lower size of noise free data (about 4000 values), Takens time delay embedding does not ensure the optimality of the reconstruction and requires to measure the smoothness of the mapping with the embedding parameters values determined by using the C-C-1 method (). We have calculated the factor F based o the statistic Rul’kov test as explained in the introduction [18] [19] . Let be the ith point in the original three dimensional state space and, a neighborhood of with a radius r. Let be the mapping of in the five-dimensional reconstructed space. The components in transformed coordinates may be written as [18] [33]

(30)

Let be, a neighborhood of with the same radius r as for. Let be the inverse mapping from the five-dimensional reconstructed space on the original three-dimensional state space. To establish that the mapping f could be able to produce a diffeomorphic representation of the original state space, it can be shown that neighbors of in may be kept by the transformation. Let be the nearest neighbor of such as, the corresponding mapping point in the reconstructed space would be a neighbor of in. Let be the nearest neighbor of such as, the corresponding point in the original space would be a neighbor of in. The factor F used to measure the mapping smoothness is given by [18] [19]

(31)

with is the number of embedded points, is the embedding dimension and T the time delay. The factor F should be closed to unity so that it would be able to characterize an ideal diffeomorphic mapping. Thus, the closer the F value is to unity, the better is the reconstruction. The F factor has been calculated for the lower size noise free data set studied in paragraphs IIId and IIIe by using the R script presented in Appendix 4. The embedding parameters found for this data set by using the C-C-1 method were and the estimated value of the F factor is 0.958. The correlation dimension has been calculated for and we found. The maximum Lyapunov exponent has been calculated for the same embedding parameters values and we found. Figure 13(a) show a trajectory in the (x, y, z) three-dimensional space obtained by integrating numerically Equation (1). Figure 13(b) shows a trajectory in a three-dimensional space obtained by considering three delay coordinates in the reconstruction space. Figure 13(a), Figure 13(b) show similarities.

5. Conclusions

This paper provides an overview of methods for embedding parameters optimal selection applied to the Rössler strange attractor reconstruction through chaotic time series. Two main approaches are used whether times series are sufficiently long free noise data set [5] [6] [7] [8] [9] or finite and noisy data set [7] [8] [33] . In the first case the embedding parameters and T can be determined independently and the theorem of Takens allows recreating the underlying dynamics. When data set are finite and/or noisy, the theorem of Takens is silent and parameters and T would appear correlated and as an irrelevant partnership between them could affect the quality of the reconstruction, the delay time window should be a more useful parameter to determine. Along to these two approaches, three methods have been presented. Coherence between the different results is discussed and robustness of all these three methods is tested. Results obtained with the Cao’s method [14] show that for noise-free data of very long length, the reconstruction is valid for any time delay as far as the embedding dimension is high enough. When going to small number noisy data samples, the time delay used to determine the minimum embedding dimension cannot have any value.

The C-C method developed by Kim et al. [7] has been applied to finite data sequence of about 4000 values and the robustness of this method has been stu- died when the original data set is degraded white Gaussian noise with different

variance σ and different strength α. Results are summarized in Table 1 and discussed. The C-C-1 method suggested by Cai et al. [8] improve some drawbacks of the C-C method and has been tested on the same time series of about 4000 values and show, T and estimates in line with Cao’s method results. Results on the C-C-1 method robustness against noise are summarized in Table 2, and shows that the C-C-1 method is an improvement of the C-C method. A criterion for determining the C-C-1 method q parameter is suggested on paragraph IIId and improves the implementation of the C-C-1 method. A technic based on the statistic Rul’kov test is proposed in paragraph IV to measure the state space reconstruction quality [18] [19] [33] .

Acknowledgements

We would like to acknowledge the Electronic, Energetic and Process Laboratory of the Reunion Island University for having us as research fellows and thank Pr Chabriat its director for having offered their facilities. We also wish to thank Professor J.C. Diels of the University of New Mexico for valuable discussions.

Cite this paper

Delage, O. and Bourdier, A. (2017) Selection of Optimal Embedding Parameters Applied to Short and Noisy Time Series from Rössler System. Journal of Modern Physics, 8, 1607-1632. https://doi.org/10.4236/jmp.2017.89096

References

Appendix 1

The C-C method organigram

Appendix 2

The C-C-1 method organigram

Appendix 3

Organigram for obtaining Q[n]

Appendix 4

Smoothness mapping F factor calculation R script

Input data: Initial time series S: ts4xnew, T (time delay) = 10, m (embedding dimension) = 5

Output data:F: F factor

are the coordinates of the initial point of the trajectory obtained by solving numerically Equation (1) with a time step deltat

library(stats)

library(scatterplot3d)

library(nonlinearTseries)

library(tseriesChaos)

X0=2.4099243

X1=2.2247949

Y0=4.0068145

Y1=4.0693054

a=0.2

b=0.4

c=5.7

deltat=(Y1-Y0)/(X0+(a*Y0))

Z0=Y0+((X1-X0)/deltat)

rosor=rossler(a=0.2,b=0.4,w=5.7,start=c(X0,Y0,Z0),time=seq(1,79.82,by=deltat))

N=length(rosor$x)

m=5

T=10

NP=N-((m-1)*T)

rosrec2=buildTakens(ts4xnew,m,T)

MATOR<-matrix(data=0.0,nrow=NP,ncol=3)

Vecsum<-vector(mode="numeric",length = NP)

for(irow in 1:NP){

MATOR[irow,1]=rosor$x[irow]

MATOR[irow,2]=rosor$y[irow]

MATOR[irow,3]=rosor$z[irow]

}

for(i in 1:NP){

XI=c(MATOR[i,1],MATOR[i,2],MATOR[i,3])

YI=c(rosrec2[i,1],rosrec2[i,2],rosrec2[i,3],rosrec2[i,4],rosrec2[i,5])

nno=neighbourSearch(MATOR,i,0.7)

nnr=neighbourSearch(rosrec2,i,0.7)

VO<-nno[[2]]

VR=nnr[[2]]

Vinto=intersect(VO,VR)

INNO=Vinto[1]

XINNO= c(MATOR[INNO,1],MATOR[INNO,2],MATOR[INNO,3])

YINNO= c(rosrec2[INNO,1],rosrec2[INNO,2],rosrec2[INNO,3],rosrec2[INNO,4],rosrec2[INNO,5])

vecxinno=XI-XINNO

deno=max(vecxinno)

vecyinno=YI-YINNO

numo=max(vecyinno)

var1=numo/deno

Vintr=intersect(VR,VO)

INNR=Vintr[1]

XINNR= c(MATOR[INNR,1],MATOR[INNR,2],MATOR[INNR,3])

YINNR=c(rosrec2[INNR,1],rosrec2[INNR,2],rosrec2[INNR,3],rosrec2[INNR,4],rosrec2[INNR,5])

vecyinnr=YI-YINNR

vecxinnr=XI-XINNR

denr=max(vecyinnr)

numr=max(vecxinnr)

var2=numr/denr

var=abs(var1*var2)

Vecsum[i]=var

}

result=sum(Vecsum)/NP