ABSTRACT

Combining with cosmological constraints we find a most probable value of 17.6 meV for beta decay anti-neutrinos. In passing we note that our expectation for the quadric Higgs self-coupling deviates from standard model expectations by a factor equal to the ud quark mixing matrix element. This matrix element also turns up by its square root in the expected triple self-coupling. We present neutrino mass eigenstates related to the neutron beta decay. In our first scenario we get 15.2 meV for the lowest mass eigenstate, in the second we get 0.917 eV. The latter is to be covered by the KATRIN experiment, while the former comes close to the CRES sensitivity in the Project 8 reach.

Keywords:

Neutrino Mass, Higgs Self-Coupling, Intrinsic Quantum Mechanics

1. Introduction

Observation of neutrino oscillations between the three lepton flavour species, 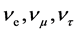[1] [2] , means that at least two different mass eigenstates have non- vanishing mass. In particular one may mention the disappearance of solar neutrinos 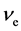[3] as a first indication for transformation of flavour states together with 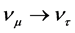oscillation [4] [5] and oscillation [6] [7] as spectacular confirmations. From the oscillations one infers mass differences between mass eigenstates. Now the task remains to determine the masses themselves. An experimental set-up, KATRIN [8] [9] [10] using tritium decay is undertaken in Karlsruhe, Germany with results for electron-based neutrinos expected in 2018¹.

We suggest the electron-based anti-neutrino mass scale to originate in a slightly misaligned Higgs vacuum [11] [12] [13] [14] [15] occurring in the neutron beta decay

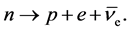(1)

In our first scenario, we find

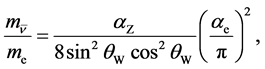(2)

which yields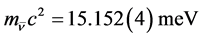. In our second scenario we find

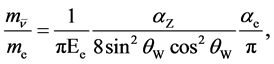(3)

with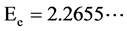, which yields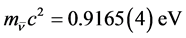. The latter is below the limit 2 eV from tritium decay [2] but above the limit 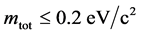on the sum-total of stable neutrino masses from cosmological phenomenology [16] .

The first scenario value is comparable in order of magnitude with [2]

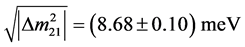(4)

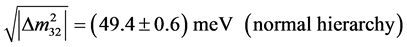
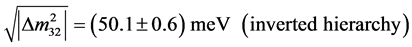
determined from the observed neutrino oscillations. The first scenario value at 15 meV positions itself intriguingly with respect to the Cyclotron Radiation Emission Spectroscopy technique of Project 8 [17] . Project 8 states a lower bound 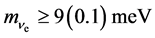from neutrino oscillations, cf. the first equation in (4) and they expect their own sensitivity level to go down to.

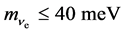Neutrino oscillations are traditionally described by mixing between left handed flavour fields via a non-diagonal matrix U relating to left handed mass eigenstates [18]

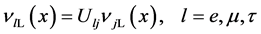(5)

From the Pontecorvo-Maki-Nakagawa-Sakata mixing matrix U one gets “effective” flavour masses. For the anti-neutrino state created in the beta decay, one has [19]

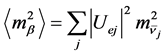(6)

where the sum runs over the mass eigenstates. It is not known whether

ends at.

We write only for the mass eigenstate in (2) and (3). In the discussion section we make a choice on hierarchy. For a three neutrino model in normal hierarchy we get from (6) our most probable mass value for the neutrino flavour generated in beta decay

(7)

2. Leptonic Sector

Both our scenarios set out from an intrinsic description of the electron, related to a similar description of the nucleon.

The value in the second scenario (3) is found from an electronic ground state on the intrinsic configuration space, the Lie group with a hamil- tonian structure

(8)

where is the energy scale and is the configuration variable. We assume the lowest neutrino mass eigenstate to be the ground state of a similar hamiltonian structure

(9)

The two Equations (8) and (9) share dimensionless eigenvalues for the ground state, i.e.

(10)

where and.

If we can solve (8) (and we can), all that is needed to determine is to fix. Below we shall present two different scenarios for the determination of.

3. The Leptonic Ground State

The particle data group notes that existing upper limits on neutrino masses imply very low masses of the order of one millionth of charged lepton and quark masses

(11)

and they conclude [20] : “It is natural to suppose that the remarkable smallness of neutrino masses is related to the existence of a new fundamental mass scale in particle physics and thus to new physics beyond that predicted by the Standard Model”.

In the present work we suggest two mass scale scenarios. The new physics component offered in that connection is the idea of intrinsic configuration variables.

The configuration variables in (8) and (9) contain four dynamical variables from the four dimensions laid out by the four generators of. Two of the generators are toroidal, i.e. diagonal matrices in a two-dimensional representation. We thus write

(12)

where are the two off-diagonal Pauli matrices

(13)

and the two diagonal generators

(14)

are represented by

(15)

The more common parametrization from using

(16)

as diagonal generators is equivalent to the choice in (15) but does not match the polar decomposition of the Laplacian which we need in order to solve (8) and (9).

The wavefunction in (8) can be factorized in a torodial and an off-torus part

(17)

in analogy with solving the Hydrogen atom in polar coordinates. The off- toroidal degrees of freedom can be integrated out to get for the measure-scaled toroidal wavefunction

(18)

with the van de Monde determinant [21]

(19)

and with potential

(20)

Here the trace potential from (8) spells out as, see Figure 1

(21)

with periodic parametric potentials [22]

(22)

and the nominator in the centrifugal term is obtained by using

for states of spin s. The constant curvature [23] term 1/4 and the centrifugal term originate in the Laplacian [24]

(23)

where are dynamical toroidal eigenangles from the two eigenvalues of the configuration variable u.

The eigenvalue of the ground state in (8), respectively (18), can be lowered by allowing period doublings in the measure-scaled torodial wavefunction, see Figure 2. This is possible because of the periodic nature of the potential which opens for Bloch degrees of freedom like in solid state physics [25] . In order that the wavefunction remains single-valued on the Bloch phase factors are

restricted to with. For 4p-periodic states we expand R in (18)

on Slater determinants [26]

(24)

with half odd-integer.

The electron rest energy is identified with the eigenvalue of the ground state in (8). In other words, is the dimensionless eigenvalue. We have determined by a Rayleigh-Ritz method [27] with 3368 base functions of the type (24) which is at the limit of our computer programme. All the integrals needed in the Rayleigh-Ritz procedure can be solved analytically (see appendix C in [28] for a similar problem) which means that can be determined with high accuracy. The potential (21) is shown in Figure 1 with a characteristic periodic structure originating in mapping to a real parameter space from the compact configuration space. An alternative basis to (24) can be constructed as Slater determinants from solutions to the one-dimensional equation

(25)

The two basis sets are both complete and yield the same spectrum as they should, but the integrals for the Rayleigh-Ritz solution based on parametric eigenfunctions from (25) can only be solved numerically. The reduced zone scheme for the lowest levels of (25) is shown in Figure 2. See e.g. [28] for more details on the parametric solutions.

4. Baryonic Sector

We have described the baryon spectrum by configurations on the Lie group with dynamics determined by a Kogut-Susskind-inspired structure [29] [30]

(26)

Here the configuration variable and is the energy scale corresponding to a length scale a which we took to be related to the classical electron radius [31] [32] by the projective relation [30] , see Figure 3

(27)

This scale reproduces accurately the electron to neutron mass ratio

(28)

with the dimensionless eigenvalue determined by solving (26). It also reproduces the and baryon spectrum with no missing resonance problem [33] . Flavour degrees of freedom are hidden in the Laplacian [24]

(29)

where [21]

(30)

and the off-diagonal generators fulfil

(31)

Colour degrees of freedom are generated by the three s, intrinsic spin

degrees of freedom are generated by the three s with commutators like body-fixed coordinate angular momenta in nuclear physics [34] . The flavour degrees of freedom are contained in the three s which connect the algebra. These mixing generators have a spectrum for determined by the hypercharge quantum number y and the isospin three component quantum number [30]

(32)

together with the spin quantum number s and the integer quantum number n which can be thought of as an intrinsic toroidal excitation number analogous to the radial quantum number in the case of the hydrogen atom in a polar decom- position like (29)

(33)

where is the angular momentum operator. Compare (33) and (29) for the term “polar decomposition”.

5. Electroweak Scale―The Higgs Connection

The transition from neutron to proton in (26) follows from a topological change in the wavefunction. For the neutronic state the wavefunction has a 2p-periodicity when parametrized in the toroidal eigenangles belonging to the three eigenvalues of u whereas for the protonic state, the wavefunction has a slightly broken symmetry with respect to the potential, namely a 4p-periodicity expressed by the appearance of fractional Bloch phase factors in the wavefunction. Such factors are allowed since the square of the wavefunction remains single-valued when extracted in parameter space, see also Bohr and Mottelson [35] for a note on doubling the angular domain for odd integer D-functions. The Bloch phase factors can lower the ground state eigen- value―provided a mechanism exists to open the relevant degrees of freedom. That mechanism is the Higgs mechanism and we connected the strong and electroweak sectors by the Ansatz [33]

(34)

with strong energy scale, torodial colour angle field, electroweak fine structure coupling and Higgs field.

We can support this Ansatz by old time quantum mechanics arguments based on the minimum quantum of action, h. The length scale a introduced above can be used for a space projection

(35)

and a time projection [36]

(36)

A full shift of 2p in the angular time variable corresponds to an exterior period determined by

(37)

leading to a minimum action

(38)

As Planck’s constant h is the minimum unit of action in the time-domain, we can use hc as a minimum unit of “action” in the space-domain, i.e. we have a minimum space action

(39)

For the exchange with the Higgs field we need a measure for the level of interaction energy. We take it to be, i.e. the electroweak fine structure coupling times the vacuum expectation value of the Higgs field. Thus the minimum space action to determine is

(40)

Equating (39) and (40) we get

(41)

With the time period from (37) and as in (26) we then

have

(42)

This settles the electroweak scale v by

(43)

corresponding to the standard model value [2] [33]

(44)

See also arguments leading up to (58).

The 2p-shift behind (42) is what is needed for the topological change leading to the period doubling in the nucleonic wavefunction, see Figure 4. In this figure, the Higgs potential

(45)

mimics the parametrized intrinsic potential. The 2p-shift in is accompanied

by a shift in the Higgs field from before the neutron decay to after the neutron decay, see Figure 4. The parameters in the Higgs potential are

(46)

We revived the pionic Goldstone modes [41] by a slight vacuum misalignment in the Higgs mechanism with a misalignment angle determined by (see Figure 5)

(47)

With the mass parameter in the Higgs potential (45) we obtained

the Higgs and pion masses determined by

(48)

and

(49)

by using the trailing

(50)

from (42). The value for the pion mass can be improved by iterative determina- tion of the fine structure constant towards the pion mass scale.

We regret not seeing the connection (50) prior to the observation of the Higgs particle since it leads to a rather accurate value for the Higgs mass, see (48). Note however, that (46) also gives a prediction for the quadric Higgs self coupling

(51)

which still remains to be tested by experiment together with our prediction [41]

(52)

for the triple Higgs self-coupling. We here used the terminology of [42] for the mass and self-coupling terms of the Higgs particle field h

(53)

expanded about a minimum of the Higgs potential [42]

(54)

The standard model values are [42]

(55)

where is the electroweak energy scale. The latter value is traditionally estimated from the Fermi constant in muon decay as [43]

(56)

On the other hand, from the vacuum expectation value at the minimum of the Higgs potential (54) one has

(57)

Since our v is based on the d to u quark transformation in the n to p decay, [44] is used, i.e. a quark mixing matrix element is introduced

(58)

In total we get for Higgs self-couplings relative to the standard model

(59)

which yields [2] and. Finally note that we actually announced the value 125.1 GeV for the Higgs mass [45] almost a year prior to the result 125.09 GeV from the combined ATLAS and CMS data [46] . Figure 6 shows the chronology.

6. Neutrino Mass Scenario II

The scale in the leptonic sector is defined by the electron rest energy in (8) as with the dimensionless eigenvalue of the period-doubled ground state of (18). Conservation of spin in the neutron decay requires the creation of the anti-electron neutrino. Thereby also the idea of lepton number conservation is introduced. As the (anti)-neutrino has no charge, we assume its creation to be mediated by neutral weak currents, i.e. the coupling

is replaced by [51] [52] , where the couplings are

determined by and from the electroweak mixing angle. To determine the neutrino energy scale we may suggest the misalignment factor to enter a trailing

(60)

analogous to (50) with the Higgs vacuum expectation value substituted by a residual electronic scale. From (60) we get for the neutrino mass

(61)

Using (47) for the misalignment, we have

(62)

The strong scale contains the classical electron radius and can therefore be expressed as

(63)

Inserting (63) in (62), using the identity

(64)

and exploiting (10), we get

(65)

This yields. The uncertainty on is estimated as, i.e. of the order of the uncertainty on corresponding to 0.022%.

7. Neutrino Mass Scenario I

Instead of the second order misalignment in the Higgs mechanism leading to the result in (65) from (60), we look in the present section for a first order misalignment but with a different length scale set by the proton and electron charges in space, i.e. the Bohr radius.

Consider the classical electromagnetic field for a proton at rest [53]

(66)

where yields the Coulomb potential energy

(67)

for an electric charge at a distance from the proton. Here we separated out the fine structure constant in order to enter into a quan- tum regime. We reinterpret as a dimensionless coupling constant in quan- tum field theory. To set up the trailing in this scenario we make the substitu- tions

(68)

to get of dimension energy at a characteristic length scale of the Bohr radius

(69)

We use the Bohr radius [2] as a characteristic scale by imagining the creation of the anti-electron-neutrino to happen at a length scale given by the electro- magnetic interaction in space between the electric charges of the proton and electron created during the neutron decay. This assumption expresses the fact that all three particles and are created simultaneously in the neutron decay. Thus, the proton and the electron charges (together with their masses)― by defining the scale of the hydrogen atom corresponding to―sets the scene for the projection of the intrinsic dynamics of the anti-electron-neutrino. If we accept (69) as a reasonable length scale, we get a trailing

(70)

where the charged current coupling is substituted by the neutral charge

coupling [51] [52] and

(71)

is the residual energy scale for neutrino mass creation. Thus the minimum space action exchange behind (70) is

(72)

Like in (37), the characteristic time is determined by

(73)

which inserted in (72) gives (70). From (70) and (10) follows

(74)

as stated in (2). With, ,

and [2] this yields

as already mentioned. To observe a neutrino mass this small would require an improvement by one and a half order of magnitude from the sensitivity of the KATRIN experiment [8] but lies close to the sensitivity of the CRES technique [17] prospected in Project 8.

8. Discussion

The second scenario with combined with the observed mass square differences (4) from neutrino oscillations means nearly degenerate neutrino mass eigenstates of the order of 1 eV. This is in conflict with cosmo- logical constraints [16] as mentioned in the introduction. For the first scenario we follow the interpretation implied by the Project 8 collaboration, that the lowest mass eigenstate should be of the order of. We infer in normal hierarchy from (2) and (4)

(75)

This leads to a sum-total

(76)

Using (6) with, and where, and [54] we infer

(77)

in accordance with what can be read off from figure 10 in ref. [55] correlating beta neutrino mass with cosmological constraints for the sum-total mass in (76) and in agreement with the disfavouring of inverted hierarchy in recent results from the NOνA neutrino oscillation experiment [56] . Note that the complex phase cancels out in the norm square of the matrix elements in (6) as does possible Majorana phases.

9. Conclusion

We have investigated two possible scale scenarios for neutrino mass generation. Both scales relate to an intrinsic conception of the origin of the Higgs potential. This conception leads to slight discrepancies from standard model expectations in the quadric and triple Higgs self-couplings by having the d to u quark mixing matrix element as a factor in the electroweak energy scale v derived from neutron to proton decay. The foundation we have suggested is that of exchange of minimum quanta of action which can be used without knowing the detailed mechanisms behind the exchange between various degrees of freedom. We look forward to future accelerator experiments to test the Higgs self-couplings and to results from KATRIN and Project 8 to determine or constrain neutrino masses and possibly clarify the mechanisms behind neutrino mass generation.

Acknowledgements

I thank my colleagues H. G. Bohr and M. S. Jensen for co-work on the Higgs mass and H. G. Bohr for co-work on the pion mass. I thank both for showing interest in the intrinsic viewpoint and I thank the Technical University of Denmark for an inspiring working environment.

Cite this paper

Trinhammer, O.L. (2017) Neutrino Mass and Higgs Self- Coupling Predictions. Journal of Modern Physics, 8, 926-943. https://doi.org/10.4236/jmp.2017.86059

References

NOTES

¹See the KATRIN homepage, http://www.kit.edu/kit/english/20624.php, where it reads: “Erste interessante Ergebnisse zur Neutrinomasse werden bereits für Mitte 2018 erwartet”. And further: “Die endgültige geplante Sensitivität erreicht KATRIN aber erst nach fünf Kalenderjahren Messzeit”, kes. 17.10.2016.