Journal of Modern Physics
Vol.08 No.02(2017), Article ID:74434,31 pages
10.4236/jmp.2017.82018
Astrophysics and Dark Matter Theory
Auguste Meessen
UCL, Louvain-la-Neuve, Belgium

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 17, 2016; Accepted: February 25, 2017; Published: February 28, 2017
ABSTRACT
Space-Time Quantization implies that the cosmic dark matter gas is subjected to pressure effects. We prove this by accounting for the mass-density distribution of dark matter in galactic halos. It can be directly deduced from observed rotation curves and coincides with theoretical predictions for dark matter atmospheres in hydrostatic equilibrium. Through embedding, the pressure of the cosmic dark matter gas prevents also the gravitational collapse of the Oort cloud, globular star clusters and cosmic filaments. The Sun has only a very small dark matter atmosphere, but observations confirm that dark matter is orbiting around the Sun. Other facts are explained by planetary dark matter disks. Space-Time quantization accounts also for dark matter-electron interaction, which allowed already for direct detection of galactic dark matter particles.
Keywords:
Dark Matter, Space-Time Quantization, Dark Matter Density Distribution, Dark Matter Rings, Pioneer Anomaly, Flyby Anomaly

1. Introduction
The idea that our universe could contain “dark matter” was unexpected. It was formulated by Zwicky in 1933, since his measurements of the velocities of nebula in the Coma cluster revealed a very high average value and a great dispersion. He analyzed this data by means of the virial theorem of statistical mechanics, which applies to any spherical distribution of equal masses, subjected to gravitational interactions. He stated [1] that “if these optical observations were confirmed, they would yield the surprising result that dark matter (dunkle Materie) is present at much greater densities than luminous matter.”
This seemed to be unbelievable, but the breakthrough came in the 1970s, because of the tenacity of Vera Rubin. She measured the redshift of many stars in the Andromeda galaxy [2] [3] [4] . The resulting dependence of orbital velocities on the distance to the galactic center required the existence of Dark Matter (DM). It had even to be present far beyond the visible boundaries of galaxies. Albert Bosma confirmed this conclusion by means of the 21-cm hydrogen line [5] [6] . He determined the mass M, which causes the observed orbital velocities by gravity. He measured also the optically detectable light intensity L and concluded that “there is a large amount of high M/L material in the outer parts.” There is not only more mass than the visible one, but it “may not be distributed in the disk at all”. Actually, it constitutes a very great spherical halo.
Nevertheless, the existence of DM in our universe is still subject to controversies. The main reason is that DM particles have not yet been identified and that measured rotation curves can also be fitted by assuming a modification of Newton’s law of gravity [7] . A recent analysis of excellent empirical data for 153 galaxies of different morphologies, masses, sizes and gas content led even to a very puzzling result [8] . The observed gravitational acceleration, determined by means of the rotation curves, was always correlated in a simple way with the baryonic acceleration, calculated by means of the distribution of luminous matter. This can suggest that DM may not be needed [9] and requires an explanation. There are also other ambiguities that have to be clarified.
Could the theory of Space-Time Quantization (STQ) be helpful in this regard? It generalizes Relativistic Quantum Mechanics by considering a finite limit for the smallest measurable distance. It is sufficient that its value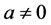 , to prove that STQ accounts for elementary particle physics [10] . It yields also insight into the nature and properties of DM particles. This solves basic cosmological problems [11] , but we want also to test the proposed theory by means of a variety of astrophysical observations. This is the essential aim of the present article.
, to prove that STQ accounts for elementary particle physics [10] . It yields also insight into the nature and properties of DM particles. This solves basic cosmological problems [11] , but we want also to test the proposed theory by means of a variety of astrophysical observations. This is the essential aim of the present article.
It may thus be useful to recall some basic consequences of the proposed theory. All elementary particles are characterized by four new quantum numbers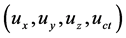 . They specify possible variations of
. They specify possible variations of 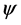 functions at the smallest possible scale along the chosen reference axes. These u-quantum numbers are subjected to a very strict conservation law when particles are transformed by annihilation and creation processes. This law determines all possible types of interactions and the constitution of compound particles [10] . We can thus distinguish three levels. 1) The basic level concerns only elementary particles. There are quarks, but also elementary DM particles, which interact with one another by exchanging gluons. Since they are electrically neutral, we called them narks. 2) On the second level, quarks get bound to one another inside nucleons, while narks can constitute various types of neutralons. Nucleons interact with one another by exchanging π mesons and neutralons by exchanging N2 bosons, composed of a nark and an antinark. This allows in both cases for scattering and the formation of compound particles. 3) The third level concerns the resulting particles. Baryonic matter is constituted of single nucleons or nuclei, where nucleons are bound together. The cosmic DM gas contains neutralons and compound DM particles, where neutralons are bound to one another.
functions at the smallest possible scale along the chosen reference axes. These u-quantum numbers are subjected to a very strict conservation law when particles are transformed by annihilation and creation processes. This law determines all possible types of interactions and the constitution of compound particles [10] . We can thus distinguish three levels. 1) The basic level concerns only elementary particles. There are quarks, but also elementary DM particles, which interact with one another by exchanging gluons. Since they are electrically neutral, we called them narks. 2) On the second level, quarks get bound to one another inside nucleons, while narks can constitute various types of neutralons. Nucleons interact with one another by exchanging π mesons and neutralons by exchanging N2 bosons, composed of a nark and an antinark. This allows in both cases for scattering and the formation of compound particles. 3) The third level concerns the resulting particles. Baryonic matter is constituted of single nucleons or nuclei, where nucleons are bound together. The cosmic DM gas contains neutralons and compound DM particles, where neutralons are bound to one another.
DM particles of any type do not interact with baryonic matter [10] , but they are subjected to gravitational interactions, because of their mass. Moreover, compound DM particles allow for fusion and fission processes everywhere in the cosmic DM gas. This accounts for “dark energy” and is important for cosmology [11] . However, DM particles are usually only scattered by one another. Because of energy quantization, elastic scattering is predominant. DM particles behave thus like molecules in ordinary gasses and the comic DM gas has some pressure. This concept will be essential for this article.
It is organized in the following way. In chapter 2, we show that the density distribution of DM inside spherically symmetric galactic halos can be directly deduced from rotation curves. This empirical result is then explained by combining gravity with pressure effects. We discuss also related problems, especially for the Solar system. In chapter 3, we consider cases where gravitational collapse of ordinary matter is prevented, since it is imbedded in the cosmic DM gas. This mechanism is especially important for the gigantic cosmic filaments, where galaxies remain separated, although they attract one another. Chapter 4 is devoted to the study of DM rings. Chapter 5 completes the previous discussion [10] of detection or production of DM particles. Instead of DM-nucleon interactions, we consider now DM-electron interactions. They explain why galactic DM particles could already be detected by means of scintillators.
2. Spherically Symmetric Dark Matter Atmospheres
2.1. Empirical DM Density Distribution in Galactic Halos
To determine the radial distribution 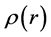 of the DM mass density in spiral galaxies, we adopt the model of Figure 1. There are many visible stars and baryonic particles in the galactic disk, but we consider only one of them. The orbital velocity v of this “test body” can be determined by measuring the Doppler shift of its radiation. Assuming a circular orbit of radius r, this implies a radial
of the DM mass density in spiral galaxies, we adopt the model of Figure 1. There are many visible stars and baryonic particles in the galactic disk, but we consider only one of them. The orbital velocity v of this “test body” can be determined by measuring the Doppler shift of its radiation. Assuming a circular orbit of radius r, this implies a radial
Figure 1. The DM atmosphere in the sphere that has the same radius r as an orbit in the galactic disk.
Figure 2. Observed rotation curves (in blue) and proposed model function (in red).
acceleration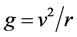 . It is due to gravitational attraction towards the center of the galaxy, but we can consider that all masses in the galactic disk are negligible with respect to the mass M of the central supermassive black hole. It follows then from Newton’s law of gravity that
. It is due to gravitational attraction towards the center of the galaxy, but we can consider that all masses in the galactic disk are negligible with respect to the mass M of the central supermassive black hole. It follows then from Newton’s law of gravity that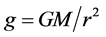 . This would yield Kepler’s law
. This would yield Kepler’s law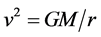 , but the observed rotation curves
, but the observed rotation curves 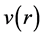 are totally different (Figure 2). When
are totally different (Figure 2). When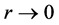 , we get a linear variation:
, we get a linear variation: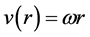 , while
, while 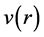 tends towards a constant value V when
tends towards a constant value V when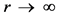 . Galactic rotation curves are said to be “flat”. Sometimes the linear increase of
. Galactic rotation curves are said to be “flat”. Sometimes the linear increase of 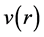 near the center of the galaxy is followed by a “bump” and the spiral arms can lead to oscillations of
near the center of the galaxy is followed by a “bump” and the spiral arms can lead to oscillations of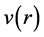 . Some rotation curves display only the rising part [7] , but this can be interpreted as resulting from a low value of
. Some rotation curves display only the rising part [7] , but this can be interpreted as resulting from a low value of  for these galaxies. We propose therefore that all observed rotation curves are (in first approximation) of the same type as the red one in Figure 2. It represents empirical results by means of the simple universal function:
for these galaxies. We propose therefore that all observed rotation curves are (in first approximation) of the same type as the red one in Figure 2. It represents empirical results by means of the simple universal function:
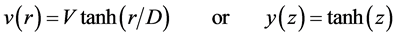 (1)
(1)
There are only two parameters: V and r, while 



Relation (1) summarizes empirical data in a unified and flexible way, by separating essential features from secondary ones. We can express this result in another way, since the rotation curve 


We expect that the mass-density 

Since the mass M is independent of r, the density 







Because of (2), we get then an integral equation:


The shape of the galactic DM density profile 












The associated functions 




The first expression was obtained by Navaro, Frenk and White [12] in 1996 and the second one in 1999 by Burkert and Silk [13] . These functions decrease, but the asymptotic variation is 



Figure 3. The empirical functions y(z) and f(z).
Figure 4. Theoretical and empirical density profiles.
2.2. Theoretical Mass Density Profile in DM Atmospheres
We will now compare the empirical profile







Since gravitational attraction towards the center of the galaxy increases the particle density n, this increases also the local pressure p. The cosmic DM gas will thus behave like the air atmosphere of the Earth. Greater pressure at lower altitude, allows for hydrostatic equilibrium. To express this condition for galactic DM atmospheres, we consider again the model of Figure 1. The mass Δm of DM contained in a portion of a very thin spherical layer of radius r will be attracted towards the center of the galaxy. For a layer of thickness dr and a portion that is delimited by a central solid angle dΩ this mass is



Because of



Galactic DM mass density profiles are always of the Einasto type, but


This follows from (2), where the mass M is negligible when


Derivation of the integral Equation (6) yields


The differential equation for 














Actually,


The results of numerical simulations led to different density profiles
2.3. Luminous Matter and Dark Matter
Initially, we thought that the very great mass M of the central black hole of galaxies is responsible for the attraction of huge amounts of DM and the spherical symmetry of halos for spiral galaxies. Because of (2), it appeared that the actual value of M is irrelevant. This suggests that a spherically symmetric DM halo could even be autonomous. It is sufficient that the central mass density ρo is very great and that the DM atmosphere is not rotating. Actually, there are so-called “voids”, where the density of luminous matter is quite low, but there is DM that could be attracted towards a small local concentration of baryonic matter. Since cosmic DM gas tends to be distributed as evenly as possible, there is no DM void. More and more DM could thus be accumulated, even when there is only a small amount of baryonic matter (BM).
This explains some recent observations. It is now possible, indeed, to localize massive DM halos by gravitational lensing. This led already in 1999 to the discovery of a “truly massive dark clump” in the cluster Abell 1942 [19] . It was said to represent a new class of objects with unusual properties, since the baryon density is there very low [20] . Even a so-called “ghost galaxy” has been detected in 2016 [21] . This Dragonfly 44 galaxy belongs to the Coma cluster and contains nearly no stars. It is “relatively round” and “nearly dark”, although the mass of DM is similar to that of the Milky Way. It seems to be a “failed galaxy”, prevented from building a normal stellar population. Its low luminosity and lack of a classical disk and bulge were said to be “anomalous”, but there are also other faint galaxies in the Coma galaxy cluster.
Dragonfly 44 was said to be “representative of an entirely new class of objects”, indicating that our understanding of the formation of galaxies is not yet sufficiently complete [22] . However, the constitution of spiral galaxies and DM halos will usually result from a synergy, leading to a statistical correlation between the amount of baryonic matter and DM in spiral galaxies. The Tully Fischer relation [23] expresses it in terms of the luminosity L and the orbital velocity V.
We mentioned in the introduction the puzzling claim [8] that rotation curves of galaxies seem to be due to baryonic matter alone. Actually, the gravitational acceleration 




2.4. The Small Solar DM Atmosphere
The motions of planets in our Solar system were correctly described without considering any DM. The mass 








The boundary condition is satisfied, since 


















Pitjec and Pitjeva [25] evaluated the upper limit for the DM density


2.5. The Stability of the Oort Cloud
The Kuiper belt is composed of small icy objects, orbiting around the Sun in its ecliptic plane between about 30 and 55 AU. It constitutes a reservoir for short-period comets, formed about 4.5 billion years ago. They are “fossils” of the origin of the Solar system and some of them can be ejected from the Kuiper belt, because of gravitational interactions with outer planets or mutual scattering. There are also long-period comets, moving around the Sun on very elongated elliptical orbits with an isotropic distribution. They were assumed to come from a spherically symmetric layer, surrounding the Sun between 50 and 100 thousand AU. The average radius of this “Oort cloud” is immense, since the closest star (Proxima Centauri) is situated at 265 thousand AU. How is it possible that the Sun attracted ordinary matter from far away and stored it in a spherical shell?
A constant mass-density 








The spherical Oort cloud protects the Solar system from undesirable intrusions, like the membrane of biological cells. However, the Oort cloud is attracted by the Sun and should collapse. This reminds us of soap bubbles. They should collapse because of surface tension, but this is opposed by a somewhat higher air pressure inside these bubbles than outside. The Oort cloud can be stabilized by DM pressure, since that requires only that the mass density 
Actually, the DM mass-density decreases progressively from 



3. Embedding Dark Matter Atmospheres
3.1. Globular Star Clusters and Elliptical Galaxies
Globular star clusters are spherically symmetric groups of 104 to 107 very old stars. It is thus astonishing that these stars could remain separated from one another. The astronomer Jeans assumed that these stars are moving around as if they were subjected to thermal agitation. He recognized, indeed, that gravitational interactions between stars should lead to mutual scattering and that their motions will be randomized [26] . He thought that globular star clusters are in hydrostatic equilibrium because of the resulting pressure. This contributes to its stability, but is not sufficient. Since BM can lead to irreversible aggregation, the equilibrium would be unstable.
Globular star clusters are actually situated in galactic DM halos, outside the visible disk. They did thus attract DM and constituted their own DM atmosphere. Although stars and DM are then subjected to common gravitational attractions towards the center of the globular cluster, they would resist collapse by means of two different pressure effects. Indeed, Jean’s thermal agitation of stars can be combined with DM pressure. The mass density 




The constant 




Elliptic galaxies are similar to globular star clusters, but they contain much more DM and stars. Many stars were so strongly attracted towards the global center of gravity, that they constituted there a supermassive black hole. Other stars remained in orbit, but not like they do in spiral galaxies. Their motions were constantly perturbed by gravitational interaction. Collapse of this swarm was not only prevented by quasi-thermal agitation. It resulted also from the fact that moving stars were embedded in a DM atmosphere. By participating in the global rotation, it justifies also the spheroidal shape of elliptical galaxies. Recent astrophysical observations confirmed that they are rotating [28] and that there is some kind of “conspiracy” between DM and stars [29] .
3.2. Cosmic Filaments and Collisions of Galactic Clusters
Cosmic filaments are the greatest structures in our Universe. They are composed of galaxies that contain stars and planetary systems, dust and hot gas. These entangled filaments constitute a cosmic web, since they are “knotted” together at places where there are superclusters of galaxies. These filaments are gigantic, but they are also associated with DM. It facilitated their formation and insures their stability. For any rectilinear portion of cosmic filaments and cylindrical coordinates, Equation (10) is replaced by

Setting

4. Rotating DM Rings in the Solar System
4.1. Formation of Planetary Systems
The Sun is at least a second generation star. When the initial stars exploded, they dispersed DM as well as BM. Both types of matter were gravitationally attracted towards the center of a new stellar system, but angular momentum had to be separately conserved. Indeed, DM particles do not collide with particles of BM and they tend to be distributed as evenly as possible. This led to the formation of a protoplanetary disk, where DM could remain in dynamical equilibrium by means of adequate orbital velocities. We have thus to expect that there is not only a small Solar DM atmosphere, but also a rather great amount of DM that is still orbiting in the ecliptic plane.
A very instructive picture of a protoplanetary disk was obtained in 2014 for the HL Tau star by means of ESOs ALMA Telescope [31] . This star is only about 1 million years old and visible matter is still distributed in large circular rings. The formation of planets resulted from gravitational accretion of baryonic matter, with a tendency to be radially distributed according to the Titius-Bode law. It is due to resonance effects for orbital motions at different frequencies [32] . However, DM particles will remain dispersed, because of elastic scattering. This means that DM rings are rotating around the Sun like planets, but they constitute a quasi-continuous radial distribution of the surface mass-density

Are there signs of the presence of rotating DM rings in our Solar system? They are not obvious, but we know that asteroids are relatively small rocky objects, orbiting around the Sun between Mars and Jupiter. They constitute a flat circular belt, extending from about 2.2 to 3.3 AU. To assume that they result from the explosion of a planet is not plausible, since the debris would have been attracted toward a local center of gravity. It is also unbelievable that they were initially distributed in a homogenous way in vacuum, but failed to merge.
Actually, we know that the inner zone of the Solar system allowed for the formation of compact solid planets, while big gaseous planets were created in the outer zone. The intermediate zone allowed only for the formation of smaller solid objects. Their mutual gravitational interactions were quite modest compared to the stabilizing effect of surrounding DM. Asteroids could thus remain separated from one another, by being embedded in rotating DM rings. They were not only limited to this region, but present everywhere in the ecliptic plane. They stabilized also the Kuiper belt, composed of small icy objects.
4.2. Gravitational Effects of a DM Disk
The existence of rotating DM rings in the ecliptic plane of the Solar system escaped attention, since their gravitational effects are small and differ from those of customary spherical matter distributions. Any material object that is situated at a distance D from the center of the Sun would be subjected to the centripetal acceleration



The radial distribution of the surface mass density 












The function 








Figure 5. Gravitational attraction by a single ring of DM.
Figure 6. 
4.3. The Perplexing Pioneer Anomaly
Telemetric measurements of the velocity of the Pioneer 10 and Pioneer 11 spacecraft revealed a small deceleration when they were moving away from the Sun [34] . This is equivalent to an additional positive acceleration, oriented towards the Sun. It was unexpected and thus said to be “anomalous” with respect to Newton’s law of gravity. When this result was published in 1998, simple causes and conceivable errors were discarded. Similar effects were even reported for other spacecraft. Figure 7 shows that the anomaly was detected for Pioneer 11, after its flyby of Jupiter (D = 5.2 AU) and Saturn (D = 9.6 AU). It increased up to the orbit of Uranus (D = 19.2 AU) and remained then nearly constant. The same value was also found when measurements were started and pursued for Pioneer 10, but there was then a slight decrease.
Unfortunately, the so-called “onset” of the Pioneer anomaly was only observed for Pioneer 11. Since Pioneer 10 had been launched one year earlier, its anomalous acceleration had not been noticed and was only measured for this spacecraft when D > 25 AU. Although the onset is a prominent feature of Figure 7, attention was only focused on the plateau. It was stated in 1998 that the “canonical” value of the anomalous acceleration is 8.74 (±1.33) × 10−10 m/s2 [35] . This value applies to both spacecraft and the essential problem was to decide between two possibilities.
Figure 7. The “onset” of the Pioneer anomaly. The anomaly was not immediately noticed for Pioneer 10.
Does the anomaly result from a force of external origin that is directed towards the Sun, or should it be attributed to a small braking force, produced by the spacecraft themselves. Being aware of the possible existence of rotating DM rings in the ecliptic plane, we wanted to see if this hypothesis could explain the Pioneer anomaly. We developed thus the theory of the preceding section and calculated 





The Pioneer 10 and 11 spacecraft had been constructed in exactly the same way and they carried two external Pu238 radioisotope power sources. The possibility of anisotropic heat radiation had been examined and rejected [34] , but a short comment of Katz [36] stated that this effect might have been “underestimated”. The NASA specialists answered [37] that enough power was available, but that the design and position of the power sources would not allow for sufficiently strong heating and anisotropic radiation of the large antenna. These sources “see” it edge on. Nevertheless, the hypothesis of a purely thermal effect came more and more in vogue.
An estimation of thermal effects by means of model calculations was published in 2008. It was asserted that recoil of IR photons could account for 35% to 57% of the canonical value [38] . This result was considered as providing “a clear indication of the possible thermal origin of the so-called Pioneer anomaly”. In
Figure 8. Calculated acceleration 

April 2012, the same authors included also diffuse reflection. This accounted for 26% - 66% of the plateau [39] . The “onset” was disregarded and the slow decrease of the anomaly was attributed to the radioactive decay of the Pu238 power sources. Rievers presented in January 2012 his doctoral thesis [40] , where he claimed that thermal effects “can explain the so-called Pioneer anomaly within a modeling accuracy of 11.5%”.
In April 2012, Turyshev et al. published the result of their own computations, based on a comprehensive model of Pioneer 10 and 11 and data available at the JPL. Evaluating thermal effects at various heliocentric distances, they found that the numerical estimate of the recoil force amounts to about 80% of the measured values [41] . However, they stated that “once the thermal recoil force is properly accounted for, no anomalous acceleration remains” and concluded even that the Pioneer anomaly “is consistent with known physics.” Another computation [42] , published in July 2013, strengthened the conviction that “solutions may be achieved that do not require the addition of any ‘unknown’ acceleration other than the one of thermal origin.”
The desire to stick to a conventional explanation was noticeable, but it could be misleading, since thermal modeling depends on many factors and no calculation did account at least for 100% of the canonical value. Moreover, the backscattering of thermal radiation could not suddenly start and increase for Pioneer 11 between 5 and 20 AU. Solar radiation pressure varies also in a smooth and predictable way. To prove or disprove the reality of the “onset” of the anomalous acceleration could have been decisive. Turyshev and his colleagues had recuperated initial data in 2005, but did not report that this input eliminated the threshold [43] . There remained uncertainties.
Since the author of this article had developed the theory of DM rings in 2012, he asked (by email on Dec. 3, 2012) if the onset was still there. Having calculated the acceleration 

4.4. Why Are Planets Not Affected?
Checking then the literature in regard to DM rings, we found that Moore and Moore [44] had also considered the gravitational effect of a DM distribution 



Moore and Moore showed that these planets are protected when they create deep trenches with steep walls in the DM distribution



We propose a mechanism that explains this apparently exotic assumption. Any planet attracts DM particles in its immediate vicinity. It creates thus a local void, but DM particles tend to be distributed as evenly as possible, because of mutual scattering. However, they have also to remain on the same orbit to insure dynamic equilibrium. They will thus move towards the planet along their normal orbit. Eventually, there remains a gap in the radial distribution of the DM mass-density distribution 
We can now use Figure 8 to estimate the surface mass-density 








4.5. The Flyby Anomaly
If the Earth did really sweep up all DM that was close to its orbit, its center would be surrounded by rotating DM rings. They are invisible and we ignore their actual distribution. Since the Earth captured DM particles that were moving with respect to the center of the Earth and are not subjected to friction, they constitute a rotating DM disk. It is situated in the equatorial plane, since it is gravitationally coupled to the spheroidal shape of the Earth. DM particles will then be in dynamical equilibrium when they are orbiting at the adequate speed with respect to the center of the Earth. Is there any evidence of such a DM disk?
It does exist, but was too unexpected to be considered at least as a possible cause of a small, but detectable anomaly. According to Newtonian gravity, a spacecraft that is approaching a planet from far away, it will turn around it on a hyperbolic path in the reference frame where the planet is at rest. The speed of the spacecraft has the same value V when it enters and leaves the sphere of gravitational influence of the planet. This symmetry is broken in the heliocentric frame, since the planet is orbiting around the Sun. The spacecraft can then acquire a higher velocity. This “gravity assist maneuver” is very useful and the result is exactly predictable, but during the Earth flyby of the Galileo spacecraft in December 1990, there appeared an unexpected velocity increase



K is a constant, when 



Figure 9 shows the hyperbolic path of a spacecraft in the geocentric system and the angles δ1 and δ2. A spacecraft of mass m is then not only subjected to the gravitational force 





For 


Figure 9. Flyby for a planet with a DM ring (see text).
Figure 10. Force causing the flyby anomaly.
When the spacecraft is relatively close to the Earth, it is necessary to consider triangles instead of parallel lines and



The force 











The constant 





Table 1 is based on data extracted from NASA’s Horizon’s web interface [54] . Only the values 





The proposed theoretical law (14) provides better agreement with observed values than (12), especially when the spacecraft passes far away from the Earth.
Table 1. Parameters for Earth flybys and the corresponding values of the observed velocity increase, while 

The main discrepancy is observed for Rosetta-1. It could result from a more dissymmetric transition from positive to negative values in Figure 10 when V and δ1 are small. Since 




We add three remarks. 1) The DM disk of the Earth is probably smaller than the orbit of the Moon (r = 385,000 km), but the Moon and satellites that are moving on smaller circular orbits in the equatorial plane of the Earth would create a circular groove in the DM disk. 2) The flyby anomaly and the Pioneer anomaly apply to unprotected spacecraft. 3) Adler tried already to explain the flyby anomaly by considering the possible existence of a DM disk in the equatorial plane of the Earth [55] . However, he assumed that DM would interact with nucleons of the spacecraft, which is negligible [10] . Here, we considered only gravitational interactions.
4.6. Global Positioning Satellites
Ben Harris concluded from a high-precion study of the motions of GPS, Galileo and GLONAS satellites that the mass of the Earth is 0.005% to 0.008% greater than the value established by the International Astronomical Union [56] . It has been stated [57] that he attributed this effect to the presence of a “disk of DM around the equator 191 km thick and 70,000 km across”. The relevant observational data and the calculations were not published, but it is not sufficient to object that “thin disks like that are generally the result of rapid rotation, while gravity tends to make things spherical” [58] . DM rings are possible.
Moreover, GPS satellites are orbiting around the Earth on circular orbits of radius r and specific inclinations (like 55˚) with respect to the equatorial plane of the Earth. The declination 




5. First Direct Detection of DM Particles
5.1. The Annual Modulation Signature
In the context of present day uncertainties about the nature and properties of DM particles, any direct detection of DM particles would be very important. Nevertheless, we have to proceed by trial and error. In general, it has been assumed that DM particles can interact with nucleons, but we have shown [10] that this is very rare. Even the most sophisticated system that was based on this assumption did not succeed [59] . Since it was not obvious what method should be used, it was suggested already in 1986 to verify if “detected” signals are genuine or not. They should display an annual modulation [60] . Indeed, the Sun is moving at about 230 km/s with respect to the galactic DM atmosphere, while the Earth is orbiting around the Sun at about 30 km/s. The flux of DM particles should thus vary every year in a specific way. This would yield at least a “significant enhancement of signal-to-background ratio”.
Fortunately, the orbit of the Earth around the Sun is not perpendicular to the “wind” of DM particles. It is inclined by about 62˚ with respect to the galactic disk. Moreover, the flux should be maximal on about June 2nd and minimal close to December 2nd. The detection rate has even to vary according to a perfect cosine function, whatever the nature of DM particles may be. It is required, however, that DM particles can be detected by the chosen method and that other possible causes of annual modulations have been excluded. In terms of these criteria, the DAMA (Dark Matter) experiment, installed in the Gran Sasso Tunnel near Rome, did succeed.
This laboratory is situated at about 1400 m under rocks and NaI(Tl) scintillators were chosen to detect galactic DM particles. First results were published in 2003 and provided already evidence of 7 annual cycles [61] . Using 9 very pure and well-protected crystals, the photomultipliers did yield a modulated counting rate. The ensemble of nearly 100 kg NaI crystals was then replaced by about 250 kg. Every one of the 25 scintillators in a protected 

The team leader Rita Bernaby and her collaborators insisted in various publications on the fact that detection occurred in a narrow energy range (2 - 6 keV). At slightly higher energies (6 to 14 keV), the annual modulation did not appear anymore. The energy calibration was regularly controlled by means of x-rays. No systematic process or other side effect could explain the ensemble of observed facts. The signature of a true detection of galactic DM particles is “stringent and unambiguous”, but why was this method successful?
5.2. The DM-Electron Interaction
The DAMA team had chosen NaI(Tl) scintillators. Although the nature of DM particles was unknown, it had thus been assumed that a DM particle that passes through a particular crystal might excite there sufficient electrons to get a detectable light flash. Bernaby and collaborators analyzed this process in 2007. They assumed that electrons might be liberated from atoms, as for ionization processes [63] . It seemed important that electrons are not at rest in their initial state, while DM particles were considered as having some great mass (~GeV/c2). The liberated electrons would then have very low energies, with a threshold effect. Similar and more sophisticated investigations followed in 2014 and afterwards [64] . We want to show here that DM-electron interactions are possible because of STQ (Figure 11) and that detection by NaI scintillators involves not only elastic collisions, but also some solid state physics (Figure 12).
Figure 11 indicates that a nark




Figure 11. DM-electron interaction is mediated by an N2 boson.
Figure 12. Momenta and possible energies, before and after an elastic DM-electron collision.
state and the antinark of the first emitted one. This yields an N2 boson, which is the mediator for interactions between DM particles, but also between DM particles and electrons. Indeed, an electon can annihilate the emitted nark to create a boson, which is the supersymmetric partner of an excited electron. Its charge Q = −1 and its mass could be relatively small, like the mass of an electron. This boson merges with the other member of the N2 boson, to recreate an electron. STQ accounts thus for elastic scattering of an electron by DM particles.
The upper left part of Figure 12 represents a DM particle and its initial momentum vector, as well as the initial momentum of one electon. We assume here identical orientations, but it will turn out that this is irrelevant. The mass M ot the galactic DM particle is unknown, but it is moving at least at 200 km/s with respect to the detector. Its initial momentum 




NaI crystals are insulators. They are excellent detectors for gamma rays, which create or liberate rather energetic electrons. For detection, it is sufficient that they excite electrons from the valence band to the conduction band of the NaI crystals. They will then move as free particles and be rapidly trapped in excited states of dispersed Tl atoms. These centers of luminescence allow for electronic transitions that yield detectable photons. The excitation of electrons and light emission occurs very rapidly and yields discrete scintillations, although many excited electrons were involved. The pulse height is even proportional to the energy of the incident particle.
DM particles can only be detected by this method when they transfer sufficient energy to electrons at the upper boundary of the valence band (E = 0) to reach the conduction band. Their energy is then




Since 


Solving for p before considering equally probable angles

The kinetic energy of the excited electron 


5.3. Detection of Galactic DM Signals
We mentioned and discussed the detection 130 GeV gamma-rays by means of NASA’s Fermi telescope and proposed a mechanism for the production of energetic photons according to STQ [10] . However, there is also an x-ray signal at about 3.5 keV. It was detected by means of the XMM-Newton x-ray telescope of the European Space Agency and by NASA’s Chandra x-ray observatory [67] . It is a very weak signal, but it appeared in stacked spectra of 73 galaxy clusters with various redshifts. Dark matter could thus be considered as the possible cause. The XMM-Newton telescope detected these x-rays for the Andromeda galaxy and the Perseus cluster, with a 
Moreover, x-rays can also result from electronic transitions when highly ionized atoms capture electrons from hydrogen atoms. However, the strongest objection resulted from the measurement of the distribution of x-ray sources at 3.5 keV in the Perseus cluster and near the center of the Milky Way. These sources did not display the radial symmetry, expected for galactic DM density profiles. There were radial and azimuthal irregularities [70] . The spatial distribution of x-rays sources at neighboring energies (between 2 and 5 keV) displayed also irregularities. Plasma emissions, due to charge transfer for highly ionized atoms, are thus very probable for these sources. Moreover, it has now been experimentally proven that that S15+ and S16+ ions capture electrons and emit x-rays near 3.4 eV [71] . The proposition that the 3.5 keV signal results from DM is questionable.
Nevertheless, skepticism should be omnidirectional. We mention 4 reasons to be prudent. 1) The detected irregular distribution of x-ray sources could result from electronic transitions, while DM signals at 3.5 eV were too weak to establish a map. 2) Since they were absent for the Virgo cluster and are always weak, they could be produced only by a particular type of DM particles. 3) The mass-density distribution 
Could the 3.5 keV x-ray signal be produced by at least one particular type of DM particles? Figure 13 shows a process that could be considered for DM particles of type N1. They were produced during the Big Bang and should still be present in our universe [10] [11] . They correspond to single narks in the (0,0,0) color-neutral state. Two N1 particles could thus meet one another and be transformed into a color-neutral gluon. According to the conservation law for u-quantum numbers, this would allow for
Figure 13. STQ could account for transformations of N1 dark matter particles into a pair of photons.
6. Conclusions
The existence of a space-time continuum seemed to be obvious, but this conviction was based on a questionable assumption [10] . We constructed thus a theory of space-time quantization (STQ), where the value a of the ultimate limit for the smallest measurable length was treated as a yet unknown parameter. It appeared that there are no logical inconsistencies when 
We did this here in various ways. STQ predicts that DM particles interact by exchanging N2 bosons and that elastic scattering is predominant for the cosmic DM gas. The resulting pressure is proportional to the density of DM particles and increases thus when the DM gas is compressed by gravitational forces. This leads to the concept of DM atmospheres in hydrostatic equilibrium. It accounts very well for observed properties of DM halos for spiral galaxies. It appeared also that the mass of the central black hole is irrelevant. DM atmospheres could even contain only a small amount of baryonic matter, as has been observed.
The same concepts were applied to the DM atmosphere of the Sun and to explain the stability of the Oort cloud. DM atmospheres are also very important to prevent gravitational collapse of globular star clusters and cosmic filaments, where stars and galaxies remain separated from one another by being embedded in DM atmospheres. Moreover, there are rotating DM rings in the ecliptic plane of the Solar system. They explain the Pioneer anomaly. We proposed a mechanism that explains how planets sweep up all DM that is orbiting at the same distance from the Sun. This does usually protect them from gravitational effects of all DM rings in the ecliptic plane. It explains also why planets have their own DM disk. It is rotating in their equatorial plane and accounts for the flyby anomaly. Properties of this DM disk can also be studied by means of GPS satellites.
We provided already some information concerning the possible production and detection of DM particles [10] . We showed here that STQ allows also for DM-electron interactions. This explains why galactic DM could already be detected by the DAMA collaboration. We advanced also some reasons to reject not yet the possibility that the weak 3.5 keV x-ray signal might be produced by light DM particles. The global conclusion is that STQ and the resulting dark matter theory withstood the test of a detailed and varied confrontation with astrophysical observations. Reality is more astonishing than we thought.
Cite this paper
Meessen, A. (2017) Astrophysics and Dark Matter Theory. Journal of Modern Physics, 8, 268-298. https://doi.org/10.4236/jmp.2017.82018
References
- 1. Zwicky, F. (1933) Helvetica Physica Acta, 6, 110-127.
http://adsabs.harvard.edu/abs/1933AcHPh...6..110Z - 2. Rubin, V and Ford, W.K. (1970) The Astrophysical Journal, 159, 379-403.
http://adsabs.harvard.edu/full/1970ApJ...159..379R - 3. Rubin, V., et al. (1976) The Astronomical Journal, 81, 719-737.
http://adsabs.harvard.edu/full/1976AJ.....81..719R
https://doi.org/10.1086/111943 - 4. Rubin, V., et al. (1980) The Astrophysical Journal, 238, 471-487.
http://adsabs.harvard.edu/full/1980ApJ...238..471R7 - 5. Bosma, A. (1981) The Astronomical Journal, 86, 1791-1824.
http://adsabs.harvard.edu/full/1981AJ.....86.1791B
https://doi.org/10.1086/113062 - 6. Bosma, A. (1981) The Astronomical Journal, 86, 1825-1846.
http://adsabs.harvard.edu/full/1981AJ.....86.1825B - 7. Brownstein, J.R. and Moffat, J.W. (2005) The Astrophysical Journal, (2006) 636, 721-741.
https://arxiv.org/abs/astro-ph/0506370 - 8. McGaugh, S.S., et al. (2016) Physical Review Letters, 117, 201101, 1-5.
https://arxiv.org/pdf/1609.05917.pdf - 9. Science News (2016) In Rotating Galaxies, Distribution of Normal Matter Precisely Determines Gravitational Acceleration.
https://www.sciencedaily.com/releases/2016/09/160921085052.htm - 10. Meessen, A. (2017) Journal of Modern Physics, 8, 35-56.
http://dx.doi.org/10.4236/jmp.2017.81004 - 11. Meessen, A. (2017) Journal of Modern Physics, 8, 251-267.
- 12. Navarro, J.F. Frenk, C.S. and White, S.D. (1996) The Astrophysical Journal, 462, 563-575.
http://arxiv.org/abs/astro-ph/9508025
https://doi.org/10.1086/177173 - 13. Burkert, A. and Silk, J. (1999) On the Structure and Nature of DM Halos.
https://cds.cern.ch/record/384623/files/9904159.pdf - 14. Einasto, J. (1965) Kinematics and Dynamics of Stellar Systems, Trudy Inst. Astrofiz. Alma-Ata 5, 87.
- 15. Merritt, D., et al. (2006) The Astronomical Journal, 132, 2685-2700.
http://arxiv.org/pdf/astro-ph/0509417v2.pdf
https://doi.org/10.1086/508988 - 16. Di Cintio, A., et al. (2010) Monthly Notices of the Royal Astronomical Society, 000, 1-11, (2013).
http://arxiv.org/pdf/1204.0515.pdf - 17. Spergel, D.N. and Steinhardt, P.J. (2000) Observational Evidence for Self-Interact-ing Cold Dark Matter.
https://arxiv.org/pdf/astro-ph/9909386v2.pdf - 18. Kruezi, L. (2015) The Case for Complex Dark Matter. Interview of James Bullock, Quanta Magazine.
https://www.quantamagazine.org/20150820-the-case-for-complex-dark-matter/ - 19. Erben, T., et al. (2000) A&A, 355, 23.
https://arxiv.org/abs/astro-ph/9907134 - 20. Capelato, H.V., et al. (2008) A&A, 492, 345.
https://arxiv.org/abs/0809.2418 - 21. van Dokkum, P., et al. (2016) The Astrophysical Journal Letters, 828, 1.
https://arxiv.org/abs/1606.06291 - 22. Feltzman, R. (2016) A New Class of Galaxy Has Been Discovered, One Made Almost Entirely of Dark Matter. The Washington Post, 25 August 2016.
- 23. Tully, R.B. and Fischer, J.R. (1977) Astronomy & Astrophysics, 54, 661-673.
http://www.wikiwand.com/sv/Tully-Fisher-relationen - 24. Read, J.I. (2014) The Local DM Density. JPhysG-100038.R1.
https://arxiv.org/abs/1404.1938 - 25. Pitjec, N.P. and Pitjeva, E.V. (2013) Astron. Zhurnal or Astronomy Letters, 39, 141-149.
https://arxiv.org/abs/1306.5534 - 26. Jeans, J.H. (1913) MNRAS, 74, 109-112.
http://adsabs.harvard.edu/full/1913MNRAS..74..109J
https://doi.org/10.1093/mnras/74.2.109 - 27. Taylor, M.A., et al. (2015) The Astrophysical Journal, 805, 1-20.
http://arxiv.org/pdf/1503.04198.pdf - 28. Caimmi, R. (2009) Serbian Astronomical Journal, 179, 31-47.
http://arxiv.org/pdf/0909.3056.pdf - 29. Cappellari, M., et al. (2015) The Astrophysical Journal Letters, 804, L21.
http://arxiv.org/pdf/1504.00075.pdf - 30. Harvey, D., et al. (2015) Science, 347, 1462-1465.
https://arxiv.org/pdf/1503.07675.pdf
https://doi.org/10.1126/science.1261381 - 31. National Radio Astronomy Observatory (2014) Birth of Planets Revealed in Astonishing Detail in ALMA’s Best Image.
https://public.nrao.edu/news/pressreleases/planet-formation-alma - 32. Bovaird, T. and Lineweaver, C.H. (2013) MNRS, 435, 1126-1138.
http://arxiv.org/pdf/1304.3341v4.pdf - 33. Nieto, M.M. (2005) Physical Review D, 72, Article ID: 083004.
http://arxiv.org/abs/astro-ph/0506281
https://doi.org/10.1103/PhysRevD.72.083004 - 34. Anderson, J.D., et al. (1998) Physical Review Letters, 81, 2858-2861.
http://arxiv.org/abs/gr-qc/9808081
https://doi.org/10.1103/PhysRevLett.81.2858 - 35. Turyshev, S.G. and Toth, V.T. (2010) Living Reviews in Relativity, 13, 1-173.
http://arxiv.org/pdf/1001.3686
https://doi.org/10.12942/lrr-2010-4 - 36. Katz, J.I. (1998) Physical Review Letters, 83, 1892.
http://arxiv.org/pdf/gr-qc/9809070v3.pdf
https://doi.org/10.1103/PhysRevLett.83.1892 - 37. Anderson, J.D., et al. (1999) Physical Review Letters, 83, 1893.
http://arxiv.org/pdf/gr-qc/9906112v1.pdf
https://doi.org/10.1103/PhysRevLett.83.1893 - 38. Bertolami, O., et al. (2008) Space Science Reviews, 151, 75-91 (2010).
http://arxiv.org/pdf/0809.2633.pdf - 39. Francisco, F., et al. (2012) Physics Letters B, 711, 337-346.
http://arxiv.org/abs/1103.5222
https://doi.org/10.1016/j.physletb.2012.04.034 - 40. Rievers, B. (2012) High Precision Modeling of Thermal Perturbations with Applications to Pioneer 10 and Rosetta, Dissert. 1-169.
http://elib.suub.uni-bremen.de/edocs/00102500-1.pdf - 41. Turyshev, S.G., et al. (2012) Physical Review Letters, 108, Article ID: 241101.
http://arxiv.org/abs/1204.2507
https://doi.org/10.1103/PhysRevLett.108.241101 - 42. Modenini, D. and Tortora, P. (2014) Physical Review D, 90, Article ID: 022004.
http://arxiv.org/pdf/1311.4978.pdf
https://doi.org/10.1103/PhysRevD.90.022004 - 43. Turyshev, S.G., et al. (2006) International Journal of Modern Physics D, 15, 56.
http://arxiv.org/abs/gr-qc/0512121
https://doi.org/10.1142/S0218271806008218 - 44. Moore, G.S.M. and Moore, R.E.M. (2013) Astrophysics and Space Science, 347, 235-247.
http://link.springer.com/article/10.1007/s10509-013-1514-2 - 45. Iorio, L. and Gioudice, G. (2006) New Astronomy, 11, 600-607.
http://arxiv.org/abs/gr-qc/0601055
https://doi.org/10.1016/j.newast.2006.04.001 - 46. Tangen, K. (2007) Physical Review D, 76, Article ID: 042005.
http://arxiv.org/abs/gr-qc/0602089
https://doi.org/10.1103/PhysRevD.76.042005 - 47. Wilkins, A. (2010) NASA.
http://io9.gizmodo.com/5584149/see-the-amazing-moon-inside-saturns-rings - 48. Anderson J.M. and Nieto, M.M. (2009) Proceedings of the IAU Symposium, 261.
http://arxiv.org/abs/0907.2469 - 49. Lämmerzahl, C., Preus, O. and Dittus, H. (2007) Astrophysics and Space Science Library, 349, 75-101.
http://www.uv.es/jfgf/Pioneer/0604052.pdf - 50. Iorio, L. (2014) International Journal of Modern Physics D, 24, 1530015, 1-35.
http://arxiv.org/abs/1412.7673 - 51. Krasinsky, G.A. and Brumberg, V.A. (2004) Celestial Mechanics and Dynamical Astronomy, 90, 267-288.
http://www.aldebaran.cz/bulletin/2009_24/GAKVAB.pdf - 52. Anderson, J.D., et al. (2008) PRL, 100, Article ID: 091102, 1-4.
http://virgo.lal.in2p3.fr/NPAC/relativite_fichiers/anderson_2.pdf - 53. Jouannic, B., et al. (2015) The Flyby Anomaly: An Investigation into Potential Causes. Proc. 25th Internat.Symp. Space Flight Dynamics, 1-17.
http://issfd.org/2015/files/downloads/papers/153_Jouannic.pdf - 54. NASA, Solar System Dynamics, Horizons Webb-Interface.
http://ssd.jpl.nasa.gov/horizons.cgi - 55. Adler, S. (2009) Is There Dark Matter in Orbit around the Earth? Institute Adv. Studies.
https://www.ias.edu/ideas/2009/adler-dark-matter - 56. Harris, R. (2013) Searching for Dark Matter using Navigation Satellites, American Geophysical Union, Fall Meeting.
http://adsabs.harvard.edu/abs/2013AGUFM.G21A0752H - 57. www.newscientist.com/article/mg22129503-100-gps-satellites-suggest-earth-is-heavy-with-dark-matter/
- 58. M. Francis.
http://galileospendulum.org/2014/01/02/no-dark-matter-is-not-messing-up-gps-measurements/ - 59. LUX (Large Underground Xenon) Collaboration (2016) Results from a Search for Dark Matter in the Complete LUX Exposure.
http://arxiv.org/pdf/1608.07648.pdf - 60. Drukier, A., Freese, K. and Spergel, N. (1986) Physical Review D, 33, 3495-3508.
http://kicp.uchicago.edu/~collar/drukier.pdf
https://doi.org/10.1103/PhysRevD.33.3495 - 61. Barnabei, R., et al. (2003) La RivistadelNuovoCimento, 26, 1-73.
https://arxiv.org/abs/astro-ph/0307403 - 62. Barnabei, R., et al. (2014) Advances in High Energy Physics, 2014, Article ID: 605659, 1-10.
https://www.hindawi.com/journals/ahep/2014/605659/ - 63. Barnabei, R., et al. (2008) Physical Review D, 77, Article ID: 023506, 1-15.
https://arxiv.org/abs/0712.0562
https://doi.org/10.1103/physrevd.77.023506 - 64. Roberts, B.M., et al. (2016) P Physical Review D, 93, Article ID: 115037, 1-23.
https://arxiv.org/abs/1604.04559
https://doi.org/10.1103/physrevd.93.115037 - 65. Alkali Halides.
http://www.ucl.ac.uk/~ucapahh/research/crystal/homepage.htm - 66. Aalseth, C.E., et al. (2014) Search for An Annual Modulation in Three Years of CoGeNT Dark Matter Detector Data.
https://arxiv.org/pdf/1401.3295v1.pdf - 67. Bulbul, E., et al. (2014) The Astrophysical Journal, 789, 23 p.
https://arxiv.org/abs/1402.2301 - 68. Boyarsky, A., et al. (2014) Physical Review Letters, 113, Article ID: 251301.
http://arxiv.org/abs/1402.4119
https://doi.org/10.1103/PhysRevLett.113.251301 - 69. Boyarsky, A., et al. (2015) Physical Review Letters, 115, Article ID: 161301.
https://arxiv.org/abs/1408.2503
https://doi.org/10.1103/PhysRevLett.115.161301 - 70. Carlson, E., Jeltema, T. and Profumo, S. (2015) Journal of Cosmology and Astroparticle Physics, 2015, 1-27.
https://arxiv.org/abs/1411.1758
https://doi.org/10.1088/1475-7516/2015/02/009 - 71. Shah, C., et al. (2016) Laboratory Measurements Compellingly Support Charge-Exchange Mechanism for the “Dark Matter” ~3.5 keV X-Ray Line.
https://arxiv.org/abs/1608.04751

























