ABSTRACT

It is in general accepted that the concept of continuous trajectories for particles is at odds with the relativistic quantum mechanics. Namely, when examining the evolution of entangled quantum objects according to frames of coordinates in relative move- ment, one gets contradictory trajectories. Such a situation is typically derived from the famous “Hardy’s paradox”. However, it is argued here that if the rationale ignores the principle of quantum contextuality, as happens typically when using Hardy’s thought-experiment, the conclusion―rejection of the assumption of trajectories―is questionable. The issue is exemplified by an additional example: the 101 property of spin 1 bosons implies conflicting trajectories when the singlet state of two such bosons is examined according to frames in relative movement. It is concluded here that in the absence of a rationale which doesn’t violate the quantum contextuality, there are no sufficient arguments for refuting the possibility of a substructure of the quantum mechanics, consisting in particles following continuous trajectories.

Keywords:

101 Property, Bosonic Singlet, Continuous Trajectories, Nonlocality, Relativity Theory

1. Introduction

The formalism of the quantum mechanics (QM) proved itself able to explain many phenomena in the microscopic world. Though, when the question is asked whether the QM is an ultimate theory, with no substructure, it is difficult to give a definite answer. The measurement process was not explained in entirety, until now, with the QM formalism. For the final step of the measurement, i.e. with a macroscopic apparatus, J. von Neumann introduced the postulate of wave-function collapse. Next, the nonlocal correlations appearing in the phenomenon of entanglement seem to imply that results of present measurements depend on data of future experiments.

Different attempts were done for eliminating the collapse postulate. A widely known attempt is due to L. de Broglie [1] , and later on to D. Bohm [2] [3] , who proposed a substructure of the QM consisting in particles which travel along continuous trajectories. For these trajectories, the wave-function is supposed to represent some sort of guide-wave, defining which trajectories are allowed and which are forbidden. Thus, when detection is reported at a certain position in space, it is assumed that a particle was present at that position prior to the detection, and that the position pertains to a continuous trajectory of the particle.

However, the Bohmian mechanics was proved unfit for explaining the evolution of identical quantum particles. As proved by P. Ghose [4] [5] [6] (see also the experiments of Brida [7] [8] ), and recently by S. Wechsler [9] , the velocity formula in Bohm’s mechanics leads to clash with the experiment.1

Though, a particular formula in some formalism may be replaced, eventually, within an improved formalism. Therefore, the present article poses a more general problem: leaving aside any particular formula, is the very idea of particles following continuous trajectories, wrong?

By continuous trajectories it’s understood here that a particle doesn’t jump from a region in space, to another region, space-separated from the former by a gap in which the wave-function is null.

Since 1992 when L. Hardy published his famous “paradox” [14] , it is believed that the idea of continuous trajectories is at odds with the theory of relativity. It is known that the theory of relativity excludes the existence of a preferred frame, s.t. the evolution of a quantum system may be examined according to any frame of coordinates and leads to the same final predictions. Hardy’s article showed that the concept of elements of reality appears as contradictory, when the evolution of two entangled particles is examined according to frames of coordinates in relative movement. The elements of reality can easily be translated into trajectories for particles, which therefore appear as contradictory―see for instance [15] [16] .

The present article brings an additional example of contradiction between trajectories. The analysis is done on the singlet states of spin 1 bosons, using the 101 property of these bosons. According to different frames of coordinates the wave-function of the system evolves differently, s.t. one infers a different pair of trajectories for the entangled particles. However, at an attentive examination, one can see that what changes from frame to frame is the quantum context: while one of the bosons―let’s name it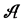― passes through an apparatus A, the other boson―let’s name it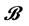―passes according to one frame through an apparatus B, and according to another frame, through an apparatus C.

The principle of quantum contextuality states the following:

Given an operator 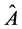which commutes with two operators, 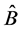and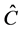, which do not commute with one another, a measurement of 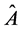together with 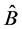may produce a different result for 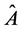than a measurement of 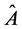together with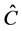; the operat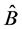or (or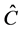) represents the context of the measurement of.

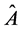For the proof of this principle see for instance [17] and the references inside, and [18] .

Berndl and Goldstein [19] applied this principle to “Hardy’s paradox” pointing to a problem with the quantum contextuality.2

The present text analyses the consequences of the contextuality on the supposed substructure. The path followed by 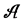when exiting the apparatus A, appears as ambiguous, depending on the frame by which one judges. Such a situation is unacceptable: if the concept of trajectories is correct, the path taken by the boson 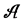is only one.

Given that the reasoning with moving frames predicts contradictory trajectories, the question arises what exactly is wrong here: the concept of trajectories, or the use of moving frames in combination with ambiguous contexts?

If a concept is wrong, it should lead to contradictions also when judging within one single frame. So, for ruling out the concept of trajectories for particles, a proof which reasons in one single frame of coordinates is needed. Whether such a proof can be done, it’s for the moment an open question.³ Anyway, as long as no such proof is available, a substructure of the QM, with particles following continuous trajectories, is not excluded.

The next sections are organized as follows: Section 2 presents the main physical properties to be used in the text. Section 3 examines the evolution of a singlet of bosons according to the QM, in a rest-frame―the frame in which the setups are at rest. Section 4 does the analysis in the light of the hypothesis of trajectories, first according to the rest-frame, then, according to a frame in movement with respect to the rest-frame. A contradiction is shown to appear, and is explained as arising from making predictions for one and the same result in the presence of differing contexts. Section 5 contains discussions and stresses questions that remain open. Section 6 contains conclusions. The Appendixes detail part of the calculi done in the text.

2. Some Properties of the Spin 1 Bosons

We are going to work, for simplicity, with a system of units in which.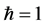

The properties of spin 1 bosons relevant here were presented in [18] . They are briefly reminded below.

Since the spin 1 bosons have the total squared spin equal to 2, given any three directions in space mutually orthogonal two by two―let’s call them X, Y, Z―the squared spin-projections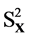, , , obey the 101 property. Namely, at a measurement of these three observables, two of them produce the outcome 1, and the remaining one produces the outcome zero.

Two spin 1 bosons can form the entangled state

(1)

where Q is an arbitrary direction in space, and are the eigenstates of the operator corresponding to the eigenvalues 1, 0 and again 1―see the formulas (A1) and (A2) in Appendix A. Note that the eigenvalue 1 is degenerated. The state (1) represents a singlet state―the total spin of the two particles is zero―see explanation in [18] .

In this text, each product of states is ordered with the state of boson on the left, and the state of boson on the right; a base like will be denoted in short as {Q}.

Four properties will be extensively used in the next sections:

(a) The state (1) is invariant at the change of the direction Q. That can be easily proved by substituting in (1) the equations (A2) with arbitrary angles θ and φ―see Appendix A, or the proof in [18] .

(b) The expression of the state (1) reveals the nonlocal property of this state, that if one particle is tested on some direction whatsoever, the other particle behaves as if it got on that direction, the same squared spin projection.

(c) If two directions are mutually perpendicular, , the operators and commute, as one can check on the matrices (A1) for two vectors P and R of angles, , respectively, , chosen so that. Therefore, the respective observables and can be measured on the same particle and in any order.

(d) For the 101 property entails:

(2)

It has to be noticed that the opposite implication is not true.

About the property (b), attention should be paid to the fact that this property acts as long as the entanglement is preserved. If the entanglement is broken, i.e. if it is truncated to a single product of independent states of the two bosons, the nonlocal correlation between particles is destroyed.

3. A Thought-Experiment and Its Quantum Analysis in the Rest-Frame

Two spin 1 bosons, and, are produced in the singlet state (1). Then, they fly apart, the boson to the station of the experimenter Alice, and the boson to the station of the experimenter Bob. Each boson passes through a series of Stern-Gerlach apparatuses (SGs), Figure 1. The SGs in each station are organized in pairs. In each pair, the first SG, called below “splitter”, splits the incident wave-packet into three wave-packets corresponding to the three spin-projections on the magnetic field direction. The second SG in the pair, called below “merger”, has the magnetic field opposite to that of the splitter, s.t. it merges the three wave-packets back into one. The magnetic field directions of the splitters are shown in Figure 2.

Note 1: with the today techniques, the SG merger doesn’t restore the wave-packets that entered the splitter, with high-fidelity. Also, these apparatuses are long, which is inconvenient too. High-precision, much smaller apparatuses are desirable. However, what is examined here is a thought-experiment, technical difficulties being left aside hoping for future improvements.

By rest-frame is understood here the frame of coordinates according to which both Alice’s and Bob’s setups, are at rest.

Note 2: in the present proof we work with the squared spin-projections. However, an SG doesn’t split a wave-packet according to the squared spin projections, but only according to the simple spin projections. We overcome the problem by placing a detector only on the central beam exiting a splitter, and/or on the beam exiting a merger. If the central wave-packet exiting a splitter produces a detection, the result obtained is. But if the wave-packet exiting a merger produces a detection, the result is.

The experiment is supposed to be performed in a dynamical way: a detector is placed on a beam after the respective wave-packet exited the SG apparatus.

Figure 1 shows that the first measurements done by the experimenters are along the direction at Alice’s station, and along the direction at Bob’s station. In this experiment we retain only the pairs which produce. That truncates the wave-function (1) to

(3)

as one can check by setting in (1), then using the transformation (A18) in Appendix A.

In continuation we describe the main steps of the evolution of the wave-function according to the rest-frame, the frame of coordinates by which all the setups are at rest.

When the boson exits the splitter the boson travels toward the merger. The wave-function describing this situation is obtained by passing in (3) from the base {} to the base {}―transformation (A17), and from the base {} to {}―transformation (A19),

(4)

One can see that if the observables and were measured, the joint result could be obtained with the probability, 4/45. This fact will have a special importance in Section 4.

Next, when the boson exits the splitter, the boson travels toward the merger. The wave-function for this situation is obtained by substituting in (4) the transformation (A16) from the base {} to the base {},

(5)

Finally the boson exits the splitter. Using the base-transformation (A15) the wave-function becomes

(6)

On this wave-function are done measurements. One can see that three combina- tions of outcomes are possible: and; or, and; or,. The combination is forbidden by the property (d), section 2, because as Figure 2 shows. Let’s stress that each one of and is measured on another particle. Though, as long as the entanglement is preserved―so happens in the wave-function (6)―the nonlocal property (b) ensures that the perpendicularity of the directions and is “felt” by both particles in the pair.

4. Analysis of the Thought-Experiment Assuming Continuous Trajectories

In this section we assume a substructure of the QM, consisting in particles traveling along definite trajectories. For distinguishing between these hypothetical particles and the bosons and possessing the standard properties of quantum objects, we denote the hypothetical particles by and respectively. We are going to try finding possible trajectories for and. We begin by seeking trajectories compatible with the wave-function as it evolves in the rest-frame―Figure 1. After that, we will seek trajectories allowed by the wave-function as it evolves according to a frame in movement from Alice’s station to Bob’s station―Figure 3.

Let’s remind that we speak here of a dynamical experiment, as said in the beginning of the Section 3. Therefore, the correlation between responses of the two bosons, if measurements were done, should have existed between the paths picked by the hypothetical particles at the exit of the splitters. Indeed, the assumption of continuous trajectories implies that the hypothetical particles don’t jump from one path to another.

In the former section was shown that if the observables and were measured, one would obtain the joint result with the probability, 4/45. Adapting this conclusion to the substructure of particles and trajectories, it entails that there is a non-zero probability that in the same trial of the experiment choose the path and choose the path a₀. It’s these trials on which we focus or attention in this section.

4.1. Analysis According to the Rest-Frame

The wave-function (5) shows that if chose the path a₀, has to choose the path―implication marked in Figure 1 by a light-blue arrow. That imposes further, according to the final wave-function (6), that may take in the splitter only a lateral path, d₊, or d_?. The state (6) is tested experimentally and the trajectories obtained above determine the outcome

and (7)

4.2. Analysis According to the Moving Frame

Let’s consider a frame of coordinates in movement with respect to the rest-frame. Passing from one frame to another one, moving with some velocity V with respect to the former, entails changes in the electromagnetic field and in the spin direction [21] . However, the velocities involved here are supposed to satisfy, s.t. these changes can be neglected, as explained in Appendix B.

The velocity V is also supposed to be tuned so as the boson exit the splitter while the boson is on its way toward the merger―Figure 3. The wave-function for this situation can be obtained by substituting in (4) the transformation (A15) from the base {A} to the base {D},

(8)

Since we consider the cases in which chooses the path, the wave-function (8) implies that exits on the path d₀-implication marked in Figure 3 by an orange arrow. At this step the boson is tested experimentally, and since is on the path d₀ the outcome is. That already contradicts the relations (7).

The outcome truncates the wave-function (8) to a product of independent states of the two bosons

(9)

obtained by retaining in (8) the terms with, i.e. the terms corresponding to. Comparing (9) with the identity (21) it becomes evident that the particle would be sent by the splitter to a lateral path. Thus, the measured joint result has to be

and (10)

It is opposite to the predictions (7). Obviously, the reason behind this contradiction is the changed context: the outcome in (8) was obtained in the context that travels on the path, while the prediction is obtained in the context that travels on the path.

5. Discussions and Open Questions

It is not the purpose of this article to advocate for a substructure of the QM, but to claim that this substructure cannot be refuted in the absence of a proof that won’t ignore the quantum contextuality―desirably, a proof within one and single frame of coordinates.

Since the substructure discussed here is at odds with reasoning by moving frames, because of the ambiguity in quantum context entailed by the latter, that means the substructure requires a preferred frame of coordinates. The theory of relativity holds that there is no preferred frame, and the relativistic QM deals by definition with the transformation of wave-functions from one frame to another. If particles follow trajectories, these trajectories should transform covariantly from one frame to another. But the previous sections showed a clash between trajectories found by different frames, not a covariant transformation. This is an argument against the above substructure.

However, entanglements have properties outside the relativistic theory of QM: instantaneous mutual influence at a distance between entangled particles is not a prediction of this theory. It isn’t produced by any type of field that transforms according to the Lorentz transformations, but by the superposition of multiparticle amplitudes which occurs in multiparticle interferometry, a phenomenon alien to the physics of the macroscopic objects.

Besides, if one denies the existence of a preferred frame, one comes to a harder problem: by the time-axis of the rest-frame, the boson is tested before the boson. If produces the outcome, the boson can produce in continuation only the response―relations (7).

However, by the time-axis of the moving frame, Section 4.2, it’s the boson that is tested before, and of course, before produces its response. The question arises, what impedes to produce the outcome (which contradicts (7))? The future response of? Is there interdependence between present and future?

6. Conclusions

The problem posed in this text was whether it is possible to assume a substructure of the QM, consisting in particles following defined, continuous, trajectories. It was argued that as long as there is no proof against trajectories within a single frame of coordinates―more exactly, a proof that does not rely on ambiguous quantum context― there is no solid ground to refute this substructure.

The analysis discussed the general possibility of trajectories for particles, in the sense that it did not restrict itself to any particular formalism for trajectories, as for example Bohm’s formalism. This generality is important because, while Bohm’s formalism was proved incompatible with the experiment, a different formalism may eventually be proved compatible. The only restriction admitted here was continuity of the trajectories, in the sense that a particle doesn’t jump over regions where the wave-function is null.

Cite this paper

Wechsler, S. (2017) Which Proof We Have against Continuous Trajectories for Particles? Journal of Modern Physics, 8, 68-81. http://dx.doi.org/10.4236/jmp.2017.81006

References

Appendix A

The general expression of the squared spin-projection operator for an arbitrary direction Q is

(A1)

Here, is the angle between the direction Q and the axis Z, and is the angle between the projection of the direction Q on the x-y plane, and the axis X. The eigenvalues of this operator are 1 and 0, the eigenvalue 1 being degenerated. We will denote by, the following eigenstates:

(A2)

and corresponding to the eigenvalue 1, and corresponding to the eigenvalue zero. These three eigenstates form a base in the vector space of states of the squared spin projection.

For the calculi that follow, one can take in Figure 1 the distance as the unit, where the notation means length of segment. Then, one easily finds that

(A3)

(A4)

(A5)

From this, one can deduce further the following angles and sine values:

, (A6)

, (A7)

, (A8)

In Figure 1 one sees that the direction A lays in the plane x-y, s.t. it makes an angle with the axis Z; with the axis X it makes the angle. Then from (A2),

(A9)

In Figure 1 one sees that the direction also lays in the plane x-y, s.t. it makes an angle with the axis Z; with the axis X it makes the angle. Therefore, using the formulas (A2),

(A10)

For obtaining the eigenfunctions of one can see from Figure 1 that the direction makes with the axis Z an angle. The projection of on the plane x-y is the direction which makes with X the angle . Using these data in (A2),

(A11)

The direction C makes with the axis Z an angle. The projection of C on the plane x-y is the direction E, which makes with X the angle

Thus,

(A12)

The direction D makes an angle with Z―see the formulas (A6)―while its projection on the plane x-y is the very axis X s.t.. Then,

(A13)

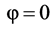
The direction makes with the angle, and its projection on the plane x-y is again the axis s.t.. Therefore,

(A14)

The following scalar products are needed in the text and can be calculated from the above sets of vectors:

(A15)

(A16)

(A17)

(A18)

(A19)

Identities:

(A20)

(A21)

Appendix B

The change in the electromagnetic field when passing from the lab frame to a frame moving with a velocity V is given by the Lorentz transformation,

(B1)

(B2)

where. We suppose here s.t. we can approximate and ignore.

No electric field acts on the bosons in the lab, , as to, (B1), it is not relevant since we assume neutral particles. Thus the fields acting on the particles are the magnetic fields of the SGs, and with the above approximations,

(B3)

The spin of a particle also changes when passing from one frame to another. Let’s denote as S₀ the spin of the particle according the frame in which the particle is at rest.⁴ In a frame moving with a velocity U with respect to the rest-frame of the particle, the spin is [21]

(B4)

The bosons in this text are considered non-relativistic particles, s.t. their absolute velocities with respect to Alice’s and Bob’s labs, satisfy. Next, the velocity V of the moving frame defined in the subsection 4.2., with respect to Alice’s and Bob’s labs, satisfies as said above. Therefore one can approximate

(B5)

Submit or recommend next manuscript to SCIRP and we will provide best service for you:

Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.

A wide selection of journals (inclusive of 9 subjects, more than 200 journals)

Providing 24-hour high-quality service

User-friendly online submission system

Fair and swift peer-review system

Efficient typesetting and proofreading procedure

Display of the result of downloads and visits, as well as the number of cited articles

Maximum dissemination of your research work

Submit your manuscript at: http://papersubmission.scirp.org/

Or contact jmp@scirp.org

NOTES

¹A debate, mainly lead by Marchildon [10] [11] [12] , arose around P. Ghose’s first articles against Bohm’s formalism, but P. Ghose refuted the criticism [13] , and later on, he proved that the Bohmian velocity leads to a contradiction in connection with the so-called “quantum equilibrium” [6] .

²Berndl and Goldstein pointed to the fact that standard QM makes predictions only for what is measured― elements of reality can’t be measured―and argued that if Hardy’s rationale would have dealt only with measured observables, the quantum contextuality principle would eliminate the paradox.

³M. Zirpel tried to do an anti-trajectory proof reasoning in a single frame of coordinates [20] . He tried to rely on CHSH-type experiments on entangled particles and on the violation of the CHSH inequalities. However, he also assumed ambiguous contexts, exactly as if working with moving frames.

⁴One has to distinguish between the frame in which the particle is at rest, and the rest-frame defined in this text as the frame in which the setups are at rest.