Journal of Modern Physics
Vol.07 No.13(2016), Article ID:70591,7 pages
10.4236/jmp.2016.713151
Influence of Recombination Centers on the Phase Portraits in Nanosized Semiconductor Films
Gafur Gulyamov1, Abdurasul G. Gulyamov2, Feruza R. Muhitdinova3
1Namangan Engineering-Pedagogical Institute,
2Physico-technical Institute,
3Namangan State University, Namangan, Uzbekistan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 12, 2016; Accepted: September 11, 2016; Published: September 14, 2016
ABSTRACT
Influence of recombination centers’ changes on the form of phase portraits has been studied. It has been shown that the shape of the phase portraits depends on the concentration of semiconductor materials’ recombination centers.
Keywords:
Recombination Centers, Phase Portrait, Generation of Charge Carriers, Recombination of Charge Carriers, Forbidden Zone, Absorption Coefficient

1. Introduction
Operation recombination processes allow to control the number of excess charge carriers in semiconductor. Control of the concentration of charge carriers has special importance at the production of semiconductor devices. There are many types of recombination such as linear recombination and quadratic one, recombination through recombination centers and radiative recombination [1] - [3] . When recombination goes through recombination centers, the transition of the charge carriers from a
2. The Continuity Equation Taking into Account the Combined Effects of Light and Variable All-Round Deformation
The continuity equation expressing the change of concentration of charge carriers is described by the following expression
 (1)
(1)
where g―rate of generation of charge carriers, r―rate of recombination of charge carriers, q―charge of electron,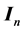 ―the current density of electrons. In uniform sample, the continuity equation has the following form
―the current density of electrons. In uniform sample, the continuity equation has the following form
 (2).
(2).
when illuminated by its forbidden zone’s light semiconductor becomes sensitive to external influences change of the absorption coefficient contributes to that [5] . At radia-
tion generation is expressed by the following expression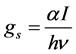 . Here, α-absorption
. Here, α-absorption
coefficient, I―intensity of the light, h―Planck’s constant, ―the frequency of the light. With the express permission of the transition frequency dependence of the absorption coefficient is
―the frequency of the light. With the express permission of the transition frequency dependence of the absorption coefficient is  where
where ―the frequency of its forbidden zone’s light [1] [3] [6] A-certain coefficient which is defined by the following
―the frequency of its forbidden zone’s light [1] [3] [6] A-certain coefficient which is defined by the following
expression  for direct allowed transitions
for direct allowed transitions 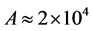 [6] , here
[6] , here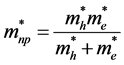 ―is the reduced effective mass,
―is the reduced effective mass,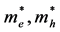 ―the effective mass of electrons
―the effective mass of electrons
and holes, respectively ―the index of refraction of the light, c―velocity of the light.
―the index of refraction of the light, c―velocity of the light.
Let’s consider the case when deformation of all-round strain effects on the semiconductor. When the deformation of band gap changes as follows [7] - [9] 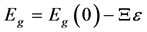 , here
, here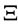 ―the constant of the deformation potential, ε―relative deformation. In the case
―the constant of the deformation potential, ε―relative deformation. In the case , then if
, then if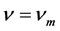 ,
, 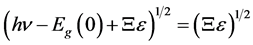 the absorption coefficient becomes
the absorption coefficient becomes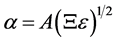 . If the deformation changes periodically
. If the deformation changes periodically

generation at light


At direct unpermitted transition frequency dependence of the absorption coefficient 

B―coefficient that is defined by the following expression

Equation (2) for direct unpermitted transition will be as follows:


Taking into account the permitted and unpermitted direct transition continuity equation takes the form

Let’s consider the case where the recombination through recombination centers takes place. According to statistics of the Shockley-Read, the rate of recombination is
described by the expression: 
tion of recombination centers, 


3. Analysis of Phase Portraits
Let’s consider the effect of deformation on a illuminated semiconductor. Let’s assume the following values: the temperature T = 300 K, the band gap Eg = 1.1 eV, the relative deformation ε = 10−6, the deformation potential’s constant is Ξ = 11.4 eV, lightl’s intensity I = 1018 cm−2∙sek−1, the effective mass off electron 






At prolonged effect of the strain, especially if the deformation is variable there is the probability of increase of recombination centers. The appearance of new defects and structural changes in the semiconductor caused by fatigue and wear material promote it. Let’s consider the effect of changes in the concentration of recombination centers in the form of phase portraits. Let the concentration of recombination centers grows increases from 2 × 1013 cm−3 to 8 × 1013 cm− 3 , in this case the phase portrait will not be in the form of a closed loop, but it will curl into a spiral form (see Figure 3). The maximum value of the carrier concentration will be 


Figure 1. Dynamics of changes of the concentration of charge the carriers in the period of variable strain.
Figure 2. Phase portrait of the concentration (n) of charge carriers versus the rate of change of the charge carrier concentration (dn/dt).
Figure 3. Phase portrait n versus dn/dt, for the case when the concentration of recombination centers variers from 


Figure 4 shows the phase portrait for the case when the concentration of recombination centers decreases from 2 × 1013 cm−3 to 2 × 1012 cm− 3 . In this case, when 



Consideration of the phase picture’s transformation at the change of the system parameters is very important for understanding the physical processes in the system. Looking at the “phase portrait” under certain given values of the parameters it is possible to imagine all the possible movements in the system for any initial values. While you observe the modification in the picture at the change of the parameters, you represent all advances that the given physical system can have for all possible values of the parameters. For example, the location and nature of the singular points on the phase plane make possible to do a number of conclusions about the processes in the system.
Research of generational process by phase portraits method has practical importance because the phase portraits give the most complete picture of what is happening in the semiconductor. This allows make diagnostics of semiconductor devices and to replace them timely for preventing interruption of their work.
Figure 4. Phase portrait n versus dn/dt, for the case when the concentration of recombination centers variers from 

4. Conclusions
Thus, the study of generation-recombination processes on the basis of the phase portraits allows us to make the following conclusions:
・ Increasing recombination centers in the semiconductor causes decrease of carrier concentration, and the phase trajectory rolls spirally toward the lowest values, both on the axis n and on the axis dn/dt.
・ Decreasing of recombination centers in the semiconductor causes with increasing carrier concentration, and the phase trajectory is set in a spiral towards the largest values as along the axis n as along the axis dn/dt.
・ The phase portraits permitted to conduct diagnostics of semiconductor devices
Acknowledgements
This work was supported by government grants of Uzbekistan F2-OT-O-15494 “Improving the efficiency of the radiators, solar cells and other optoelectronic devices based on quantum dot research and hetero nanostructure exciton and bipolaron transport phenomena”, F2-FA-0-97004 “Dynamics of solitons in ultracold quantum gases, and optical systems and synergistic processes in multicomponent semiconductors” and F2-21 “Mathematical modelling of the determination of the density of surface states at the semiconductor-insulator”.
Cite this paper
Gulyamov, G., Gulyamov, A.G. and Muhitdinova, F.R. (2016) Influence of Recombination Centers on the Phase Portraits in Nanosized Semiconductor Films. Journal of Modern Physics, 7, 1661- 1667. http://dx.doi.org/10.4236/jmp.2016.713151
References
- 1. Bonch-Bruevich, V.L. and Kalashnikov, S.G. (1977) Semiconductor Physics. Nauka, Moscow, 674 p.
- 2. Abakumov, V.N., Perel, V.I. and Yassievich, I.N. (1991) Nonradiative Ecombination in Semiconductors. In: Agranovich, V.M. and Maradudin, A.A., Eds., Modern Problems in Condensed Matter Sciences, North-Holland, Amsterdam, 376 p.
- 3. Bonch-Bruevich, V.L., Zvyagin, I.P., Karpenko, I.V. and Mironov, A.G. (1987) Problems in Physics of Semiconductors. Nauka, Moscow, 144 p.
- 4. Baranskiy, P.I., Klotchkov, V.P. and Potykevich, I.V. (1975) Semiconductor Electronics. Naukova Dumka, Kiev.: 704 p.
- 5. Bir, G.L. and Pikus, G.E. (1972) Symmetry and Strain-Induced Effects in Semiconductors. Nauka, Moscow, 584 p.
- 6. Gulyamov, A.G. (2015) World Journal of Condensed Matter Physics, 5, 60-65.
http://dx.doi.org/10.4236/wjcmp.2015.52009 - 7. Polyakova, A.L. (1979) Deformation of Semiconductors and Semiconductor Devices. Energy, Moscow, 168 p.
- 8. Pankove, J.I. (1971) Optical Processes in Semiconductors. Prentice-Hall, Inc., Englewood Cliffs, 457 p.
- 9. Gulyamov, G. and Gulyamov, A.G. (2015) Semiconductors, 49, 819-822.
http://dx.doi.org/10.1134/S1063782615060111 - 10. Gulyamov, G., Gulyamov, A.G. Ergashev, A.Q. and Abdulazizov, B.T. (2015) Journal of Modern Physics, 6, 1921-1926.
http://dx.doi.org/10.4236/jmp.2015.613197 - 11. Kireev, P.S. (1975) Semiconductor Physics. Vishaya Shkola, Moscow, 584 p.






