Received 23 October 2015; accepted 13 December 2015; published 16 December 2015

ABSTRACT

Electrodynamics of the one-electron currents due to the circular orbital motion of the electron particle in the hydrogen atom has been examined. The motion is assumed to be induced by the time change of the magnetic field in the atom. A characteristic point is that the electric resistance calculated for the motion is independent of the orbit index and its size is similar to that obtained earlier experimentally for the planar free-electron-like structures considered in the integer quantum Hall effect. Other current parameters like conductivity and the relaxation time behave in a way similar to that being typical for metals. A special attention was attached to the relations between the current intensity and magnetic field. A correct reproduction of this field with the aid of the Biot-Savart law became possible when the geometrical microstructure of the electron particle has been explicitly taken into account. But the same microstructure properties do influence also the current velocity. In fact the current suitable for the Biot-Savart law should have a speed characteristic for a spinning electron particle and not that of a spinless electron circulating along the orbit of the original Bohr model.

Keywords:

One-Electron Orbital Current in the Hydrogen Atom, Electrodynamical Properties without and with the Electron Spin, Electron Microstructure

1. Introduction

The electrodynamics of the electron motion in atoms is rather seldom discussed. The Bohr model of the hydrogen atom concerns mainly the mechanical effects due to the presence of the electron motion in the atom. In particular these are the velocity, angular momentum and energy of the electron particle. The electrostatic force between nucleus and electron applied in calculations defines the geometrical distance which separates both elementary particles composing the atom, but the electric field as such does not enter the formalism. The energy differences define the spectroscopic properties of the atom; however―at the same time―the magnetic effects connected with the electron motion seem to be fully neglected. The aim of the present paper is―in the first step ―to bridge this magnetic gap. Next the electron motion on an orbit is considered as a current and parameters of that current (potential, intensity and resistance) are examined. In a further step the electron is considered as a particle moving in a conductor having a definite conductivity constant. This constant, as well as the length of the free path and relaxation time connected with it, are all applied in a study of the Ohm’s law for the one-electron orbital current in the atom.

A separate problem concerns a reference of the geometrical microstructure of the electron particle to its electrodynamical properties. In fact an examination of the electron current along the orbits leads to two concepts of the current intensity: one of them neglects totally the electron spin, but in another one the spin effect is directly involved. Our aim is to discuss a connection of the electron microstructure and spin with the current intensity in some detail.

2. Magnetic Field Due to the Electron Motion Present in the Atom and Its Consequences

A circular motion of the electron particle along the orbits provides us necessarily with the magnetic field directed normally to the orbit planes. The strength of the field

B must fit the frequency

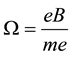(1)

of the circular orbital motion. In effect the strength 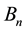obtained for any orbit n should satisfy the relation

(2)

where

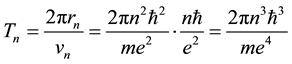(3)

is the time period of the electron circulation along the orbit n. The orbit radius [1] [2]

(4)

and the electron velocity

(5)

on the orbit are taken into account in (3).

A substitution of 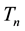into (2) gives the relation

from which

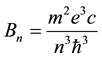(6)

indicating the change (decrease) of with an increase of n.

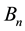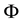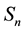Physically the effect of the change of with n is especially characteristic when the magnetic flux across the orbit area is considered. Assuming a constant on the orbit area we obtain

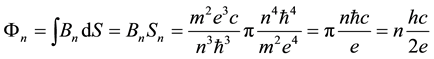(7)

since

(8)

Equation (7) implies that the change of the magnetic flux due to the electron transition between the orbit and n becomes

(9)

The obtained in (9) is identical with the magnetic flux quanta observed experimentally in superconductors [3] [4] . In the present paper this will be applied in a study of the electrodynamical properties of the electron motion in the hydrogen atom; see [5] [6] .

3. Maxwell Equations and the Electric Resistance Characteristic for the Orbital Motion

A constant current can exist only in the presence of the electric field of a non-electrostatic nature; see e.g. [7] . We assume that the electric field active along the orbit n is due to the time change of B from to. The fields and are coupled by the Maxwell equation

(10)

[8] . When the both sides of (10) are integrated over the geometrical parameters characteristic, say, for some orbit n they give

(11)

Let the interval be that given in (9), whereas is the time interval necessary for the electron transition between the orbits nad n. In a preceding paper [9] we have shown that is coupled with the transition energy from level to n, viz

(12)

by the formula

(13)

It should be noted that entering (13) approaches the time period given in (3); see [5] [6] [9] .

Because the field intensity can be a constant number along the orbit n, we obtain from (9), (11) and (13) the relation

(14)

The left-hand side of the formula (14) defines the electromotive force connected with the electron motion along the orbit n, so―when the absolute value of is considered―we have

(15)

4. Electric Resistance of the Orbital Motion

The electric resistance R is the ratio between the electromotive force and the current intensity i obtained in course of the transition time:

(16)

Here the formula (13) is again taken into account. This gives together with (15):

(17)

We find R independent of the size of parameters and. In effect R is the same constant number for all orbits n. Moreover, the value of R is equal to one-half of the electric resistance associated with the integer quantum Hall effect; see e.g. [10] .

5. Electric Conductivity and the Length of a Free Path of the Electron

Let us define the electric conductivity by the relation

(18)

so

(19)

On condition the absolute value of (14) is taken into account, we obtain

(20)

Therefore from (16) and (19)

(21)

The formula for the contribution of a single electron to the metal conductivity is [11]

(22)

where is a free path of the electron being in the state n. A comparison of (21) and (22) indicates that

(23)

is a free path in the case of the electron being in the orbital state n of the hydrogen atom.

The in (23) divided by the electron velocity gives the relaxation time of the conduction process. In the present case this is

(24)

Evidently the in (24) differs solely by the factor of from the time period in (3). The approximate value of for is sec; it increases with an increase of n.

6. The Ohm’s Law Referred to the Size Properties of the Conductor

If the electric field has a potential, so, the integral of performed along a closed current path becomes equal to zero [7] . This means that solely the field due to the time change of B can provide us with associated with the current. We demonstrate here that a typical connection between the current conductivity and the field strength concerns not i alone but also a modified current

(25)

The term is the cross-section area of the current.

A comparison of (25) with (19) gives the relation

(26)

In fact we shall find that the resistance in (17) can be represented by

(27)

which is a well-known formula; see e.g. [7] . Evidently with the aid of

(28)

which is the length of the orbital conductor, we obtain

(29)

This is a result equal to the resistance R calculated before; see (17).

7. Microstructure of the Electron Particle and the Current Intensity

The influence of the geometrical microstructure of the electron particle on the current intensity seemed to be a neglected problem. In the present Section we try to demonstrate that in fact such influence can be of importance. One of the typical relations of electrodynamics connecting the magnetic field intensity B and the current j is (see e.g. [12] )

(30)

The integral on the left of (30) is extended along a closed current path which in case of an electron orbit n is

(31)

On the other side of (30) the current is crossing a planar area normal to which is equal to

(32)

In order to estimate for the one-electron current we refer it to the microstructure properties of the electron particle represented by a small charged sphere [7] [8] . The particle has the radius

(33)

Therefore we assume that for a one-electron orbit is equal to

(34)

In principle two concepts concerning the current along the orbit n can be applied. The first of them is that

(35)

In this case we obtain on the left of (30) the expression

(36)

But the right-hand side of (30) gives from (3) and (35)

(37)

which is a result being in a full disagreement with (36). The ratio of (37) to (36) gives

(38)

where is the well-known fine-structure atomic constant:

(39)

But another situation is attained when instead of in (35) we assume the current density

(40)

Here is the electron velocity given in (5) and is the density of the electron particle

(41)

This kind of current has been applied in calculating the Poynting vector associated with the energy emission in the hydrogen atom; see [9] .

By applying the current intensity of (40) we obtain for the right-hand side of (30) the formula

(42)

The result of (42) differs from the left-hand side of (30) calculated in (36) solely by the factor of 3/2.

A direct application of―instead of―can be done in a check of the Biot-Savart law for the electron current in the hydrogen atom. According to this law [12]

(43)

Since

(44)

and the integral on the right of (43) gives

(45)

we obtain for in (43)

(46)

which remains in a perfect agreement with the formula (6).

8. Time Interval Entering the Current Velocity and Its Reference to the Electron Spin

The aim of this Section is to examine the physical background of the difference between and; we find that velocity entering should be associated with the electron spin. If in (40) is a correct expression for the current, which means that it satisfies the Biot-Savart law, a reference of to the intensity i―defined by a simple ratio of e and time T―is given by the formula

(47)

Here T is an unknown time interval which has to be calculated.

The current is due to the electron orbital motion in the hydrogen atom, but in a previous approach to i―where the formula for has been neglected―we had [9]

(48)

and was the time interval of the spinless orbital motion about the atomic nucleus given in (3).

Let us transform (47) into the expression

(49)

and assume the motion along the orbit for the sake of simplicity. The next step is a transformation of (49) into

(50)

because of

(51)

and

(51a)

This gives

(52)

where the last term refers to the formula (39) for.

Therefore we found that T for the current i in (47) should be approximately

(53)

times smaller than. Because the time period of the spin circulation satisfies the relation [13] [14]

(54)

we find that T in (52) entering the current in (47) does approach the time period of the spin circulation and not characteristic for the spinless motion along the electron orbit having the index.

A natural question is how the number given in (52) is changed with the change of n. Since the velocity of a spinning electron does not change with n remaining close to c [13] [14] , the number of spin loops along the electron trajectory increases proportionally to:

(55)

see (4). The driving velocity for the electron motion becomes equal to the orbit velocity [7] [13] :

(56)

This holds for any n; cf. (5) and (56). The symbol is the size of the static electric field acting on the electron. Because we obtain

(57)

spin oscillations within the time period.

We found that electrodynamics of the current in which the size of the electron particle is taken into account is much different than electrodynamics where this size is neglected. Equation (46) shows that for the one-electron current the Biot-Savart law is satisfied in the first case, but does not hold in the second current case; see (36) and (37). In fact the momentary (local) velocity of the current becomes much different in each of the two examined cases. For the electron particle having a definite size this velocity approaches the speed characteristic for a spinning electron; see (52) and (54). On the other side, the speed of electrons with a neglected size [see (5) and (48)] is equal to the average speed of the electron along its orbit; this is a much lower speed than of a spinning particle. In the Bohr theory the average speed on the orbit is also a local speed of a spinless electron particle.

9. Summary

The electron orbital motion in the hydrogen atom is considered as a one-electron current, and parameters of that current, like intensity and electric resistance, are examined in some detail. The calculations are done on the basis of the formula for the time change of the magnetic field induced by the electron motion in the atom; see (10) and (11). The result obtained for resistance is independent of the orbit index n and equal to one-half of the quantum of resistance observed in the integer quantum Hall effect examined for the planar crystalline structures. On the other hand, a calculation of the conductivity constant for the orbits depends on n and gives results formally similar to those calculated for metals.

The relaxation time, being the ratio of the free-electron path and electron velocity on the orbit, attains for the index―the value of sec. This increases gradually with n attaining already for small n―the value similar to that characteristic for the in metals.

In principle the current intensity does not depend on the electron velocity but is solely a function of the electric charge and the time connected with the charge flow [9] . However, an attempt to obtain a correct size of the magnetic field from the basic laws of electrodynamics, for example the Biot-Savart law, requires an insight into the microscopic (geometrical) properties of the electron particle combined with the use of the notion of the electron velocity.

A characteristic result is obtained when a spinless current (48) having is applied to calculate in accordance with the Biot-Savart law. In this case the size of should be reduced to that of. We have instead of (43):

(58)

This equality holds if we note that

(59)

which is identical with in (6) and (46).

But the same property concerning the Biot-Savart law can be obtained for which is the magnetic field intensity for the electron spin [14] . In this case we have

(60)

and the spin circulation frequency is

(61)

is the time period of the spin circulation and

(62)

is the current intensity on the loop travelled by a spinning electron.

A substitution of the above spin parameters in place of and, together with the radius of the electron microparticle being unchanged, into the formula representing the Biot-Savart law in (59) gives

(63)

The result (63) remains in a perfect agreement with presented in (60).

We find in general that the velocity connected with the orbital motion, but coupled with a negligence of the microstructure properties of the electron particle, does not give a correct result for B. For example the size of B characteristic for the Bohr orbital motion in the hydrogen atom can be reproduced with the aid of the Biot-Savart law when a much higher local speed―namely that associated with a travelling of the electron along the spin loops and not that along the Bohr orbit―is taken into account.

Cite this paper

StanislawOlszewski, (2015) Electrodynamics of the Electron Orbital Motion in the Hydrogen Atom Considered in Reference to the Microstructure of the Electron Particle and Its Spin. Journal of Modern Physics,06,2202-2210. doi: 10.4236/jmp.2015.615224

References